基于相位调制的高精度测时理论研究

张 朗，孔德仁，贾云飞

（南京理工大学 机械工程学院，江苏 南京 210094）

在炮口测速装置中，需要将弹丸初速值作为弹道参数送入引信内置微处理器，并结合其他弹道参数，计算出引信装定时间。为了实现精确控制炸点，大幅度增加弹丸毁伤概率，必然要求引信的定时精度很高［1］，从而需要一种高精度计时方法。此外，在破片速度测量中，由于破片在飞行过程中姿态不稳定，速度变化不是一个平稳的过程，为了定量评判破片在某个瞬间或某个特征点的瞬时速度，在采用平均速度法v＝Δs／Δt时，要求区截装置的距离Δs尽可能小，而Δt尽可能趋近于零，这就对时间间隔的测量精度提出了很高的要求。

目前，常规测时仪一般采用脉冲计数法原理研制而成，测量精度通常为0.1μs，已经不能满足炮口引信装定和破片速度测量的精度要求。采用倍频的方法虽在一定程度上可以提高测时精度，但过高倍频存在晶振稳定度及抖动等问题。此外，倍频系数过高，大多数数字电路无法正常响应［2］。因此，对高精度测时方法进行理论研究，寻求一种误差较小、精度高的综合方案十分有必要。

1 时间间隔测量原理

在炮口引信装定及破片测速试验中常采用区截装置测速法，其中时间间隔的测量通常在电子电路中转换成两个脉冲信号边沿之间的时间间隔测量，其测量原理如图1所示［3］。被测时间间隔由3部分组成：①脉冲计数法得到的基准时钟整数部分NTp；②启动脉冲信号上升沿与紧接着的基准时钟上升沿之间的时间间隔ΔT1；③截止脉冲信号上升沿与紧接着的基准时钟上升沿之间的时间间隔ΔT2。

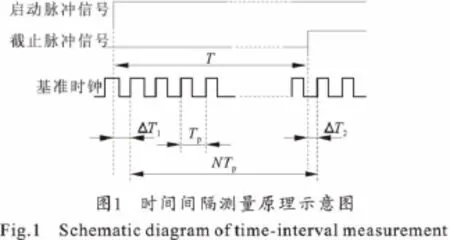
设被测时间间隔为T，则有：

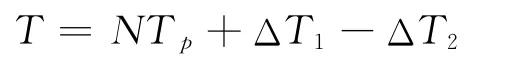
而脉冲计数法得到的是计数脉冲个数N，因此时间间隔的测量值：

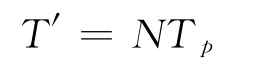
由此可知，脉冲计数法的测量误差为：

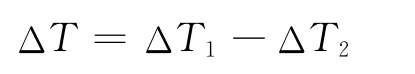
其最大值为一个时钟周期Tp。该误差称为脉冲计数法的原理误差，产生的原因是待测脉冲上升沿与基准时钟上升沿的不一致。原理误差的存在限制了时间间隔的测量精度，比如当基准时钟频率为10 MHz，即T＝时，误差将达到0.1μs，已p经不能满足一些高精度测时的场合。

为了克服脉冲计数法的原理误差，一方面可以提高基准时钟的频率，这带来的问题是时钟频率越高对电路的要求越高，并且相应的芯片也很难选择；另一方面，利用模拟电路将ΔT1、ΔT2扩展后进行二次量化，但是模拟电路部分难以集成，非线性难以消除，而且二次量化仍然存在原理误差［4－5］。基于此，提出一种相位调制的测时方法，利用时钟的相位信息对ΔT1、ΔT2进行测量，有效地提高了测量精度。

2 相位调制技术

相位调制技术的思路是将传统的基于高速时钟计数的时间测量方法转化为采用多路多相时钟进行时间测量。时钟信号经过精确数字移相，形成N路频率相同，相位依次相差360°／N的多相时钟信号。将其分别作为N路时间间隔测量的基准时钟，并通过计数器在各自的时钟周期内进行计数。图2为相位调制测时原理框图。

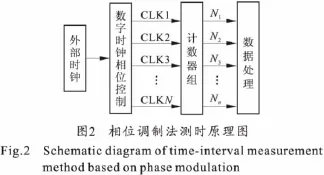
用相同计数闸门（启动／截止）对获得的一系列规律性相位顺延的参考时钟集｛CLKi｜1≤i≤N｝分别计数，得到N个计数值Ni。其中可以提取出启动信号和截止信号上升沿与紧接着的基准时钟上升沿之间时间间隔最小的两路信号，记为第l路和第m路，l≥1，N＞m。这两路信号的相位分别为φl、φm，若对第m路时钟的脉冲计数值为Nm，则时间间隔测量值：

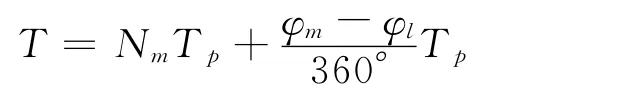
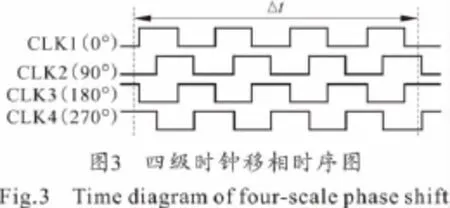
图3是四级移相时序图［6］，将400MHz时钟经四级延迟，每级相位滞后90°。单用一个时钟CLK1对启动／截止信号的时间间隔测量时，可记得4个时钟周期，得到的结果为10ns。采用相位调制技术，由于从CLK1到CLK3记到的时钟个数是4，CLK4记到的时钟个数为3，于是：

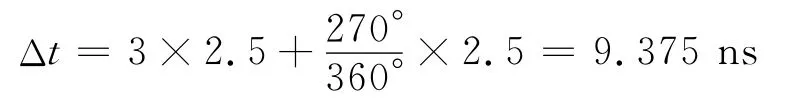
测量精度提高了4倍。

可以看出，相位调制技术实际等效于将原始计数时钟进行倍频，从而提高测量精度。同时，该方法保证了电路的最大工作频率不变，避免了时钟频率过高带来的一系列问题。

3 测时系统总体设计及仿真

在基于相位调制技术的时间间隔测量中，系统实现的关键部分是保证送入各计数器的时钟相对延迟精度，即要保证计数时钟之间的相位差。由于原始时钟频率经倍频后已经相对较高（400MHz），因此时钟的延迟时间只有几纳秒，使用普通的延迟线芯片无法达到精度要求［7］。同时为了避免电路板内芯片传送延迟的影响，保证测时系统的精度和稳定性，拟采用FPGA来实现提出的测量方法。系统总体设计如图4所示。

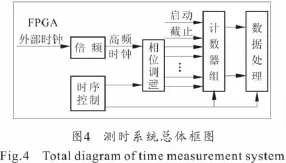
测量系统实现的关键是相移时钟的产生，该部分可由FPGA中时钟管理模块PLL实现［8］。选用Altera公司的Stratix III系列FPGA，内部有6个PLL，可以产生16路移相时钟。首先将外部高精度时钟芯片产生的时钟从PLL专用引脚输入FPGA后连接到PLL0的inclk0端，PLL0将其倍频至400 MHz后作为基准时钟，并输出4路基准时钟给PLL1、PLL2、PLL3和PLL4。PLL1～ PLL4通过FPGA内部全局时钟线并联，每个PLL的inclk0输入端分别和PLL0的输出端c0～c3相连。4个PLL的控制信号完全一样，但每个PLL中4个输出时钟相位设置不同，依次递增22.5°，对应的时间差为156.25ps，即构成了16路相移信号。

图5是在QuartusII环境下利用16个8位计数器对锁相环输出的16路移相时钟信号进行计数的仿真结果。锁相环输入频率为20MHz，倍频系数为20。从图中可以看出第1～12个计数器计数值为01001111，即79个时钟周期，换算成时间间隔为197.5ns；第13～16个计数值为01001110，即78个时钟周期，由相位调制原理可得测量结果为：

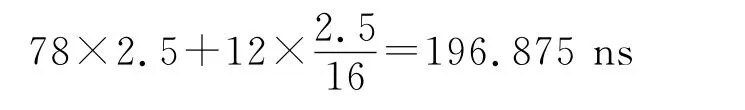
测量精度大大提高，仿真结果满足理论预计结果。

4 结 论

文章提出并实现了一种基于相位调制技术的高精度测时方法。与传统测量方法相比，该法可在不提高基准时钟频率的情况下，进一步提高测量精度，降低因使用高频时钟所引起的对器件速度、稳定性等提出的要求。此外，该法易于在FPGA中实现，扩展灵活，集成度高，可广泛应用于炮口引信装定及破片速度测量等高精度时间间隔测量的领域。

（References）

［1］鲁新凯，蔡倩，朱艳.高精度电子时间引信的研究与设计［J］.水雷站与舰船防护，2009，17（2）：5－7.LU Xin－kai，CAI Qian，ZHU Yan.Research on and design of high－accuracy electronic time fuze［J］.Mine Warfare ＆ Ship Self－Defence，2009，17（2）：5－7.（in Chinese）

［2］孙杰，潘继飞.高精度时间间隔测量方法综述［J］.计算机测量与控制，2007，15（2）：145－148.SUN Jie，PAN Ji－fei.Methods of high precision time interval measurement［J］.Computer Measurement ＆Control，2007，15（2）：145－148.（in Chinese）

［3］宋建辉，袁峰，丁振良.脉冲激光测距中高精度时间间隔的测量［J］.光学精密工程，2009，17（5）：1046－1050.SONG Jian－hui，YUAN Feng，DING Zhen－liang.High precision time interval measurement in pulsed laser ranging［J］.Optics and Precision Engineering，2009，17（5）：1046－1050.（in Chinese）

［4］PIOTR DUDEK，STANISLAW SZCZEPANSKI，JOHN V HATFIELD. A high－resolution CMOS time－to－digital converter utilizing a vernier delay line［J］.IEEE Transactions on Solid－State Circuits，2000，35（2）：240－247.

［5］BOWMAN M J，WHITEHEAD D G.A picosecond timing system［J］.IEEE Transactions on Instrumentation and Measurement，2007，26（2）：153－157.

［6］郑卉卉，程少云.基于数字移相的高精度到达时间测量系统［J］.计算机测量与控制，2007，15（4）：429－431.ZHENG Hui－hui，CHENG Shao－yun.System of precise measurement of toa based on digital phasic shift［J］.Computer Measurement ＆Control，2007，15（4）：429－431.（in Chinese）

［7］SZPLET R，KALISZ J，SZYMANOWSKI R.Interpolating time counter with 100ps resolution on a single FPGA device［J］.IEEE Transactions on Instrumentation and Measurement，2000，49（4）：879－883.

［8］叶超，冯莉，欧阳艳晶.基于FPGA的高精度时间间隔测量仪设计［J］.信息与电子工程，2009，7（2）：159－163.YE Chao，FENG Li，OUYANG Yan－jing.A design for the precise time－interval measuring instrument based FPGA［J］.Information and Electronic Engineering，2009，7（2）：159－163.（in Chinese）