抑制PMSM周期性转矩脉动的迭代学习方法

李兵强， 林辉

(1.西北工业大学自动化学院，陕西 西安 710072;2.西北工业大学电气工程博士后流动站，陕西 西安 710072)

0 引言

永磁同步电机(permanent magnet synchronous motors，PMSM)广泛应用于高性能伺服系统中，然而转矩脉动的存在影响了电机在速度控制系统中的低速性能和位置控制系统中的高精确度定位，降低了系统精确度，恶化了系统性能，会引起系统振动和噪声，严重时还会威胁系统运行安全。另外，在直接驱动系统中，由于没有齿轮等机械环节，电机转速非常低，转矩波动将会毫无衰减地作用到被控对象上，影响系统性能。为此，必须采取措施尽量减小系统的转矩脉动。从20世纪80年代永磁同步电机伺服系统进入实用化以来，转矩脉动最小化问题就受到了很大重视。经过多年的研究，产生了很多方法，这些方法主要分为两类［1］，即改进电机设计和改进控制方法。

进行合适的电机设计，调整电机结构使其性能更接近理想性能。通过改进电机设计来削弱转矩脉动主要有斜槽或斜极、改进定子绕组形式、改进定子和转子磁路等方法［1－4］。这些方法能有效地减小齿槽转矩和纹波转矩。然而，这些方法无一例外地会增加电机的加工难度和成本，同时，还会降低电机的性能。另外，仅仅依靠电机设计的方法减小转矩脉动，在很多场合已不能满足高性能伺服系统的性能要求，因此必须从其他方面考虑对电机转矩脉动进行补偿。

随着微电子技术和现代控制技术的发展，运用现代控制理论的各种控制方法，通过控制定子电流的波形来控制转矩脉动的方法越来越受到重视。这些方法主要有反电势倒置法、编程电流控制法、反馈控制方法、智能控制方法以及自适应控制方法等［5－10］。反电势倒置法和编程电流控制法等属于开环控制，本身具有较大的缺陷，对电机和逆变器参数的漂移、外界的干扰均无法加以补偿，因而在实际应用中抑制转矩脉动的效果有限。反馈控制方法通过转矩和磁链观测器来产生反馈信号，从而削弱转矩脉动，但其控制精确度会受到电机参数变化的影响，并且对电机参数变化而带来的转矩脉动不能有效地消除，使得控制作用变差。智能控制方法和自适应控制方法虽然在一定程度上克服了电机参数时变的影响，但实现复杂，目前技术条件下的实用性不强。

对于永磁同步电机的恒压频比控制，通过负载角闭环控制，在提高系统稳定性并保持高效率的同时，也可有效抑制转矩(转速)波动［11］。另外，Xu等［12－13］将迭代学习控制(iterative learning control，ILC)应用于永磁同步电机的矢量控制中，通过在线学习并补偿交轴电流分量来抑制转矩脉动，取得了令人满意的效果。本文分析了转矩脉动主要分量的周期特性，并基于此特性，借鉴Xu等的控制思想，将迭代学习控制技术应用于永磁同步电机恒压频比控制中，通过迭代学习补偿电机控制电压来抑制转矩脉动。设计了控制器结构，进行了收敛性分析，最后进行了仿真研究。

1 PMSM转矩脉动分量周期特性分析

在分析转矩脉动时，作如下假设［14］:不考虑永磁体和转子的阻尼效应;转子励磁磁场对称分布;并且定子电流不含偶次谐波。

为产生恒定电磁转矩，要求永磁同步电机的电动势和电流均为正弦波。但实际上，永磁励磁磁场或定子绕组的空间分布不可能是完全正弦的，所以感应电动势的波形一定会发生畸变。由逆变器馈入的定子电流，尽管经过调制可以逼近正弦波，但其中还含有许多高次谐波。一般情况下，转矩脉动主要由纹波转矩和齿槽转矩两部分组成。纹波转矩由感应电动势或电流波形畸变引起，是转矩脉动的主要部分。齿槽转矩由定子齿槽或者铁心磁阻的变化引起，与定子电流无关。

1)纹波转矩及其周期特性

若定子为Y联接，且没有中线，则定子相电流中不含3次和3的倍数次谐波［14］。于是，在定子电流基波分量与感应电动势基波分量同相位的情况下，可得电磁转矩为

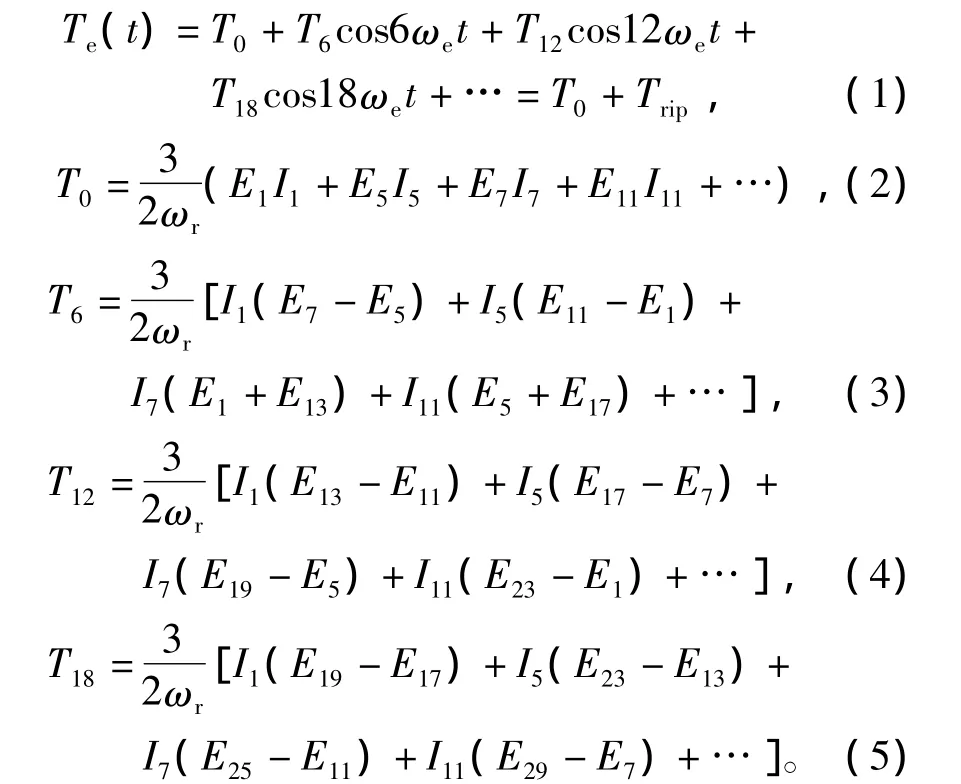
式中:T0为平均转矩;Trip为纹波转矩;T6、T12和T18分别为6次、12次和18次纹波转矩;ωe为转子电角速度;ωr为转子机械角速度;E1、E5和E7分别为感应电动势1次、5次和7次谐波;I1、I5和I7分别为定子电流1次、5次和7次谐波。

上述分析表明，次数相同的感应电动势和电流谐波作用后产生平均转矩，次数不同的感应电动势和电流谐波作用将产生脉动频率为基波频率6倍次的纹波转矩，各纹波转矩的幅值与感应电动势和电流波形的畸变程度有关，其主要成分是6次纹波转矩。可见，纹波转矩具有明显的周期特性，其周期为1/6电角周期。

2)齿槽转矩及其周期特性

转子转过一个齿距λ后，两侧产生的转矩脉动之和便构成了齿槽转矩，如图1所示。可以看出，这是一个周期函数，其基波分量波长与齿距一致，而且基波分量是齿槽转矩的主要部分。图1中，λ为齿距(机械角度)。

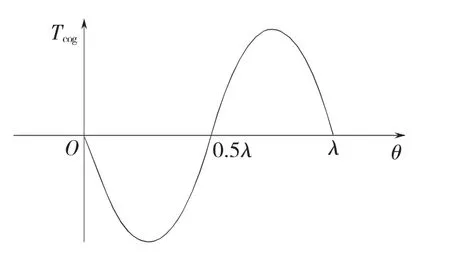
图1 齿槽转矩示意图Fig.1 Cogging torque curve

所以，齿槽转矩也具有明显的周期特性，其周期为齿距的机械角度。

迭代学习控制是一种对做重复运动的轨迹跟踪系统的控制方法［15］，通过使用先前控制中的数据信息，可以通过在线迭代寻找到合适的控制输入，理论上可以获得非常精确的跟踪轨迹。由于永磁同步电机转矩脉动主要成分存在明显周期特性，可以通过迭代学习控制来抑制其周期性转矩脉动，提高伺服精确度。

2 利用迭代学习控制补偿周期性转矩脉动

2.1 控制器结构

由前文分析可知，永磁同步电机电磁转矩包含平均分量和脉动周期分量，即

本文上述内容提到，怀远县开发了许多石榴的附加价值。政府应该通过技术研发，深入挖掘石榴的各种用途，提高产品价值，延长产业链。在种植园区附近规划土地开设工厂，将农村剩余劳动力招入工厂，也可以吸引多数农民工回乡就业，或者招募附近县乡的剩余劳动力进入工厂。在石榴收获后，直接将卖相差、品质佳的石榴运入工厂进行果皮分离。将石榴皮交由专门人员负责晒干后打包销售给各个中药店。而分离出来的果肉去籽后进行榨汁后加工售出。而石榴籽可以提取精油进行售卖。口感酸涩的石榴就可以进入酒厂加工成石榴酒出售。一系列加工线的形成能够延长产业链，提高农产品附加值。促进怀远石榴产业化发展。

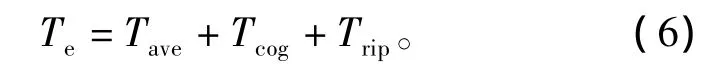
式中:Tave为转矩平均分量;Tcog为齿槽转矩;Trip为纹波转矩。脉动周期分量的一个周期T可取2pπ电角度，即电机机械一圈，p为转子极对数。

由永磁同步电机机械运动方程可得电机转速和转矩间的传递函数为

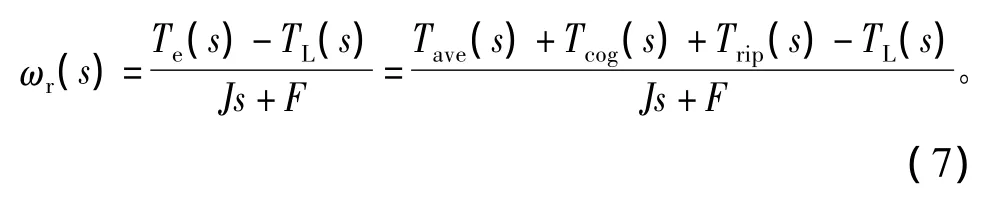
式中:TL为负载转矩;J为折合到电机转轴上的转动惯量;F为摩擦系数。可见，转速将会产生和转矩一样谐波频率的纹波。为了减小转速纹波，必须减小转矩脉动。然而，抑制转矩脉动需要获取实时转矩值，目前有两种方法可以实现:1)使用转矩传感器测量转矩，这会使整个系统过于昂贵并且转矩测量带宽有限，不利于实时转矩的获取;2)使用转矩观测器估计转矩，这会使系统过于复杂并且无法对非电量引起的转矩脉动进行观测，例如齿槽转矩、转子偏心、轴承系统摩擦转矩不均匀以及负载扰动等。

在实际应用中，往往关注电机转速是否稳定，并且所有类型的转矩脉动都会引起转速波动，因此可以直接对转速纹波进行补偿，从而间接地补偿了转矩脉动。然而，这种方法的不足是动态特性依赖于速度检测的带宽，适于电机低速运行时的补偿，高速时，由于转子惯量的滤波特性，转速波动已经不是那么明显，一般也无需再进行补偿。

图2为基于迭代学习控制的永磁同步电机恒压频比控制框图。图中，ωr，k+1(θ)为角速度反馈，是电角度θ的函数，ωrefr为转子参考角速度。电机暂态运行时，控制电压为由恒压频比控制曲线所得电压U0;达到稳态后，电机控制电压为U0与由迭代学习控制所得补偿电压ΔUk+1(θ)之和，即

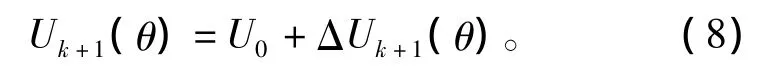
迭代学习律采用开闭环学习律［15］，其数学描述为

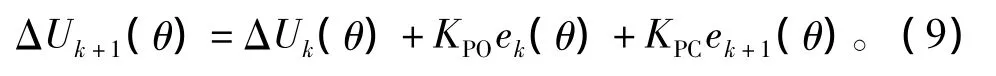
式中:ΔUk+1(θ)和 ΔUk(θ)分别为闭环和开环补偿转矩(转速)纹波的电压分量;ek+1(θ)和ek(θ)分别为当前周期和上一周期角速度误差，为电角度θ的函数;KPO和KPC分别为开环增益和闭环增益;k为周期数，即迭代学习开始后电机运转的第k圈。

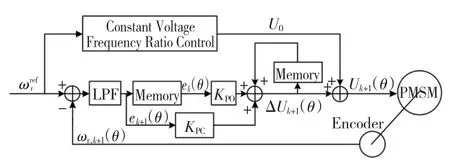
图2 基于迭代学习控制的PMSM恒压频比控制框图Fig.2 Block diagram of PMSM constant voltage frequency ratio control with ILC

2.2 收敛性分析

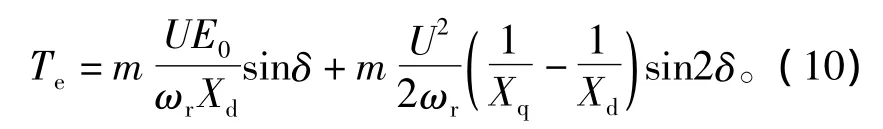
式中:m为电机相数;U为相电压;E0为反电动势;δ为矢量U与E0之间的夹角，即为负载角;Xd为直轴同步电抗;Xq为交轴同步电抗。为分析方便，考虑面装式永磁同步电机，有

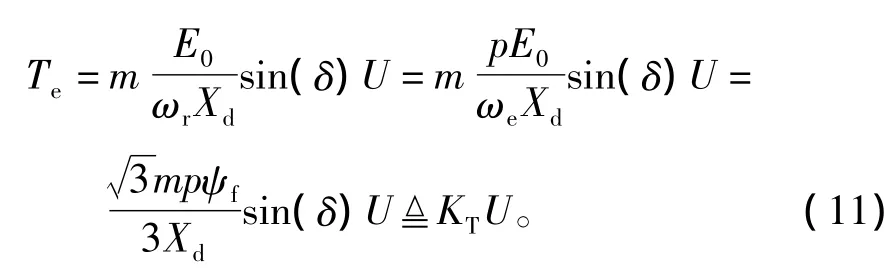
式中:ψf为永磁体磁链;KT为转矩系数。

由永磁同步电机机械运动方程可得

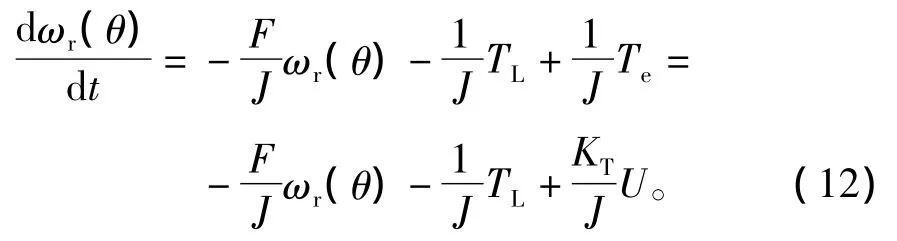
令状态变量x=ωr(θ)，系统输出y=Te，控制输入u=U，由式(11)和式(12)可得系统数学模型为

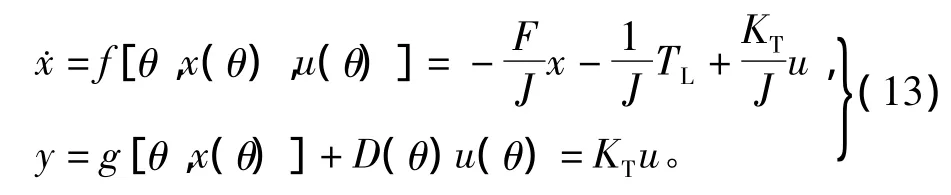
可知 g［θ，x(θ)］=0，系统输出直接馈通项 D(θ)=KT，由文献［15］可知迭代学习律(9)的收敛条件为

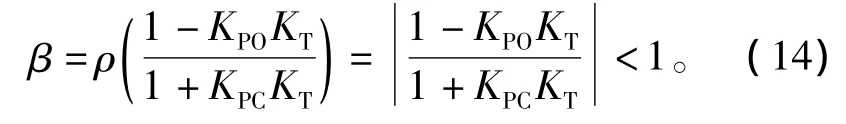
式中:ρ为谱半径。

3 仿真及结果分析

基于上述控制策略，在Matlab/SIMULINK环境下建立系统仿真模型，系统仿真结构如图2所示。电机参数为:额定电压为300 V;额定转速为9200 r/min;额定转矩为0.32 N·m;定子电阻为14.0 Ω;d轴电感为18.7 mH;q轴电感为18.7 mH;永磁体磁链为0.1385 Wb;转子转动惯量为7.26×10－5kg·m2;极对数为1。

仿真参数为:迭代学习开环增益KPO=0.002，闭环增益KPC=0.02，满足式(14)的迭代学习控制收敛条件;电机负载为0.32 N·m;设由纹波及齿槽效应引起的转矩脉动为0.01cos6ωet+0.005cos12ωet;摩擦系数 F=3.035 ×10－4N·m·s·rad－1。电机采用恒压频比控制，待稳定运行在200 r/min后加入迭代学习控制。

定义转矩纹波系数和转速纹波系数分别为

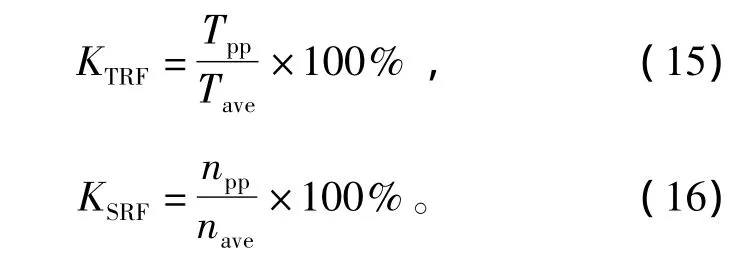
式中:Tpp为转矩纹波峰峰值;Tave为平均转矩;npp为转速纹波峰峰值;nave为平均转速。

图3和图4分别为学习初始时刻转速初始误差不为零和为零时电机的响应特性，即迭代学习每次初始运行时刻的初始误差不为零或为零。通过对比可知，当初始误差不为零时，已不满足迭代学习控制的收敛性条件，即每次运行时的初始误差为一收敛到零的序列［15］，转矩、转速和调制度会产生明显的尖峰和振荡，并且随着学习过程的进行有加剧的趋势;而当初始误差为零时，满足迭代学习控制的收敛性条件，迭代学习过程可快速收敛，转矩、转速和调制度不会产生尖峰和振荡，随着学习过程的进行其脉动逐渐减小。因此，初始学习时刻应选择转速误差为零的时刻，如图4中的0.2924 s时刻。

由图4可知，电机每旋转一转，进行一次迭代学习，可有效减小转矩(转速)脉动，并且学习次数越多，控制效果越好。图4中从0.2924 s开始学习，每0.3 s(2π机械角度)学习一次，当学习4次后，转矩纹波系数为3.1%，远小于初始时刻的11.2%，并且由图4可知转矩纹波为高次谐波，很容易被转子的惯性作用滤除;转速纹波为4%，也远小于初始时刻的42.5%。

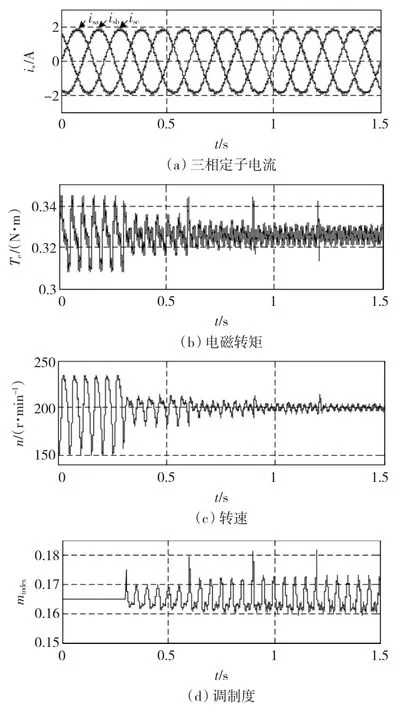
图3 学习初始时刻转速误差不为零的响应特性Fig.3 Response as initial speed error is not zero

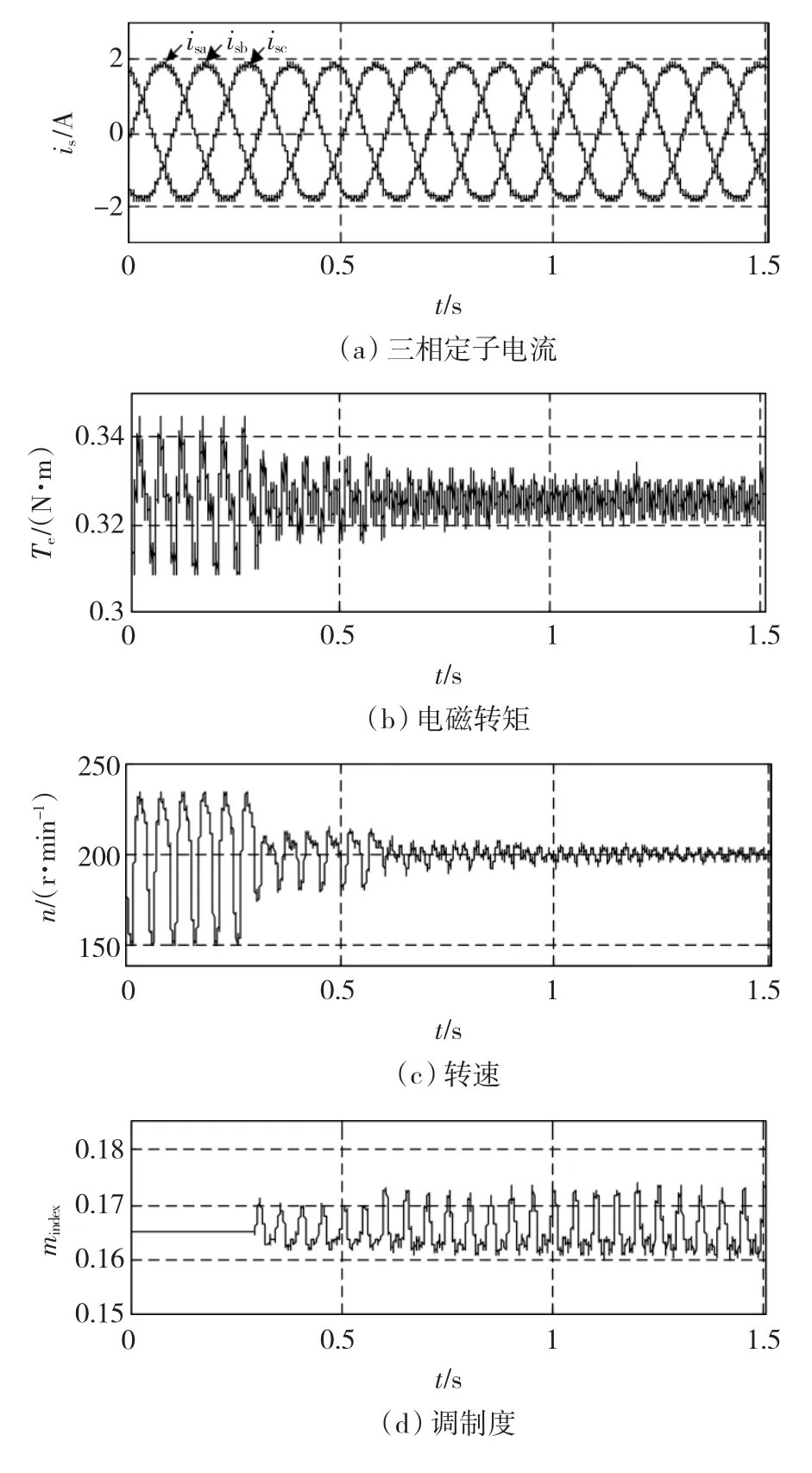
图4 学习初始时刻转速误差为零的响应特性Fig.4 Response as initial speed error is zero

4 结语

永磁同步电机低速运行时存在转矩脉动问题，这严重影响了伺服性能。通过迭代学习控制在线补偿控制电压可以有效抑制转矩脉动。仿真结果表明，所提方法不但保持了恒压频比控制结构简单、调速方便的优点，而且有效解决了低速转矩(转速)脉动大的问题，并且算法实现简单，对原控制系统改动量小，不依赖于系统的先验知识和系统参数，鲁棒性强。

［1］JAHNS Thomas M，SOONG Wen L.Pulsating torque minimization techniques for permanent magnet AC motor drives-a review［J］.IEEE Transactions on Industrial Electronics，1996，43(2):321－330.

［2］ISLAM Rakib，HUSAIN Iqbal，FARDOUN Abbas，et al.Permanent-magnet synchronous motor magnet designs with skewing for torque ripple and cogging torque reduction［J］.IEEE Transactions on Industry Applications，2009，45(1):152 －160.

［3］DOSIEK Luke，PILLAY Pragasen.Cogging torque reduction in permanent magnet machines［J］.IEEE Transactions on Industry Applications，2007，43(6):1565 －1571.

［4］KANG G H，SON Y D，KIM G T，et al.A novel cogging torque reduction method for interior-type permanent-magnet motor［J］.IEEE Transactions on Industry Applications，2009，45(1):161－167.

［5］张爱玲，王震宇，杨文杰.直接转矩控制系统中减小转矩脉动方案的比较［J］.电机与控制学报，2008，12(5):566 －570.ZHANG Ailing，WANG Zhenyu，YANG Wenjie.Comparison between two kinds of reducing torque ripple of based on direct torque control［J］.Electric Machines and Control，2008，12(5):566 －570.

［6］HUNG J Y，DING Z.Design of currents to reduce torque ripple in brushless permanent magnet motors［J］.IEE Proceedings B:Electric Power Applications，1993，140(4):260 －266.

［7］HANSELMAN Duane C.Minimum torque ripple，maximum efficiency excitation of brushless permanent magnet motors［J］.IEEE Transactions on Industrial Electronics，1994，41(3):292－300.

［8］卢达，赵光宙，李楠.包含零矢量的永磁同步电机直接转矩控制［J］.电机与控制学报，2010，14(9):1 －6.LU Da，ZHAO Guangzhou，LI Nan.Direct torque control with zero-voltage vector for a permanent magnet synchronous motor［J］.Electric Machines and Control，2010，14(9):1 －6.

［9］CLENET S，LEFEVRE Y，SADOWSKI N，et al.Compensation of permanent magnet motors torque ripple by means of current supply waveshapes control determined by finite element method［J］.IEEE Transactions on Magnetics，1993，29(2):2019 －2023.

［10］CHO K Y，BAE J D，CHUNG S K，et al.Torque harmonics minimisation in permanent magnet synchronous motor with back EMF estimation［J］.IEE Proceedings:Electric Power Applications，1994，141(6):323 －330.

［11］李兵强，林辉.新型永磁同步电机高精度调速系统［J］.中国电机工程学报，2009，29(15):61 －66.LI Bingqiang，LIN Hui.Novel high-precision speed regulation system for permanent magnet synchronous motor［J］.Proceedings of the CSEE，2009，29(15):61－66.

［12］XU Jianxin，PANDA S K，PAN Yajun，et al.A modular control scheme for PMSM speed control with pulsating torque minimization［J］.IEEE Transactions on Industrial Electronics，2004，51(3):526－536.

［13］QIAN Weizhe，PANDA S K，XU J X.Speed ripple minimization in PM synchronous motor using iterative learning control［J］.IEEE Transactions on Energy Conversion，2005，20(1):53－61.

［14］王成元，夏加宽，杨俊友，等.电机现代控制技术［M］.北京:机械工业出版社，2006:103－105.

［15］林辉，王林.迭代学习控制理论［M］.西安:西北工业大学出版社，1998:24－26.