用于微弱信号检测的改进Duffing混沌电路性能分析

胡文静， 刘志珍， 厉志辉

(山东大学电气工程学院，山东 济南 250061)

0 引言

用Duffing振子的临界相变检测微弱信号是当前微弱信号检测领域的研究热点，该方法即有重要的理论意义，也有广泛的实际应用价值。例如目前很多研究尝试将其用在金属检测、振动测量、勘探地震学等领域，近年来很多理论研究都表明Duffing振子检测噪声背景下微弱正弦信号从精确度和信号识别能力上要好于一些传统的检测方法。相关研究文献也越来越多［1－4］，但这些文献大多局限于 Matlab仿真，尚未深入研究Duffing振子的电路实现问题，即使个别的EWB仿真电路也仅适用于很低频率(ω=1 rad/s左右)的情况，而且也未见其对噪声背景下电路检测微弱信号的能力有深入研究，从而限制了其真正的应用［5－6］。本文在分析当前存在问题的基础上，提出了一种改进的电子线路，适当调整该电路参数，可实现从低频到高频的微弱正弦信号检测。通过进行Multisim仿真，对该电路在较高频率ω=106rad/s(159155 Hz)下临界阈值、检测微弱信号的性能及抗噪声能力进行了进一步的深入研究。电路中的器件均采用实际器件且对应具体型号，为使Duffing振子检测微弱信号走向实用提供依据。

1 Duffing振子及其电路实现

1.1 Duffing混沌系统检测微弱信号的原理

本文研究在混沌弱信号检测中常用的Homes型的Duffing方程，其状态方程为

式中:n(t)为白噪声;ω为待测信号的频率。该系统主要检测依据是:噪声背景中的微弱正弦信号会使该系统由混沌态向大尺度周期态跃变。根据异宿轨道Minikev方法判定，以上方程只是在频率较低的情况下，其Poincare映射中稳定不变流形与不稳定不变流形才会相交，出现横截同宿点，进而可能出现混沌解。为了检测较高频率的信号，可从原方程出发，经过时间尺度变换得到一个新的动力学方程［6］为

该系统在较高频率时仍具有从混沌到大尺度周期态的临界相变，在新的相空间(x－y)中，x，y的相速度提高了ω倍，因此可改变方程中的ω来适应外界不同频率的信号检测。为了方便电路实现，将式(2)写成积分形式为

式中C1和C2为积分常数，当n(t)=0，如果x(0)=0，y(0)=0，则 C1和C2均为0。要用电路实现式(3)少不了积分环节，在电路实现时，如果对式(3)先乘以ω，后积分，由于 ω较大，例如本文中采用ω=106rad/s，电路的直流偏置电源只有－15 V和+15 V，电路就会瞬间饱和。因此这里巧妙地采用先积分后乘以ω的方式设计电路，从而避免了该问题，使电路实现高频信号检测成为可能，这也是本文的创新之处，在当前研究混沌微弱信号检测的文献中没有见到。目前已有的Duffing振子EWB仿真电路，多是根据式(1)设计的，电路只适用于频率很低的情况，即使调整电路参数，可测信号的频率范围也很有限，且都是采用虚拟器件［5］，没有采用具体型号的实际器件。

1.2 Duffing混沌电路的设计

式(3)可通过正弦电压源、模拟运算放大器、模拟乘法器、电阻、电容及热噪声模块实现。

为了方便说明，能较清晰的看出式(3)各量之间的运算关系，首先给出电路的运算框图，如图1所示。图1中R1C1是由运算放大器组成的差动反相积分器的时间常数，R8C2是反相积分器的时间常数，R1C1和R8C2均和下面图3中的电路元件相对应。

一般情况下由运放组成的积分器如图2所示［7］。其输入和输出电压满足

输出电压Uo正比于输入电压Ui的积分，其比例系数为－1/(RC)。所以运算框图1中的R1C1，R8C2均是考虑该比例系数引入的。

图1 Duffing电路的运算框图Fig.1 Operational black digram of the Dufffing circuit

图2 模拟积分器Fig.2 Analog intergrator

图3是设计的Duffing振子电路，电路中的元器件均采用实际器件，运算放大器采用3554 AM，并对其进行了Multisim仿真。该电路的优点是只要对R1C1，R8C2做合适的调整，该电路即可检测低频信号也可检测较高频率的信号。拓宽了Duffing电路的检测范围。例如本文中 ω取106rad/s(f=159155 Hz)，则反相放大器1的放大倍数为

考虑到运算放大器的性能，单级运算放大器的闭环放大倍数以小于100为宜，不妨取K1=100，则R1C1=K1/ω =100/1000000=10－4。

然后根据差动积分器的设计方法［8－10］，选取合适的R1和C1，这里取

同样，反相放大器2的放大倍数K2取10，则R8C2=K2/ω =10/1000000=10－5，然后选取合适的R8和 C2，这里取R8=1 kΩ;C2=10 nF。

如果ω取其它值，调整方法同上，这样通过适当调整R1C1，R8C2，就可以适应不同频率的检测。另外图3中其它电路元件分别取R1=R2=R3=R4=R6=R8=R10=1 kΩ，R7=100 kΩ;R11=10 kΩ;R12=20 kΩ;R13=R14=10 kΩ;R5=R9=10 kΩ，R5和R9是为了解决积分漂移而引入的直流负反馈电阻。直流偏置电源V2=V4=V6=V8=V10=－15 V;V3=V5=V7=V9=V11=15 V。

图3中的运算放大器在Multisim器件库中选取3554 AM，其原因简述如下:其开环增益A=100000，输入失调和电流分别为Vos=0.0005 V和Ios=4×10－12A，较高的开环增益和微小的输入失调量可有效减少计算误差和积分漂移。为了使波形不失真，输出电压U0的上升斜率必小于运放的最大摆率。其摆率为1.2×109V/s，可保证波形不失真。

另外，Multisim器件库中只有虚拟乘法器，如图3中的A1～A4所示。实际应用中乘法器的选取主要考虑到频率和摆率，可选取AD734BQ。

图3 Duffing混沌电路图Fig.3 Duffing chaotic circuit

2 电路仿真及性能分析

2.1 基于初值敏感性检测的性能

用Multisim仿真软件对图3电路进行了仿真，Multisim是集设计与仿真于一体的虚拟“电子工作台”。其作用很接近实际的电子试验台。可用其设计、测试、调试电路和进行各种仿真分析。这里设定仿真系统绝对误差限10－12;相对误差限0.001，电源频率选取f=159155 Hz，Multisim中电源电压为有效值，为方便起见，r取有效值［11－12］。根据电路图3并结合运算框图1不难知道:结点①的电压u1为方程(2)中的x，结点②的电压u2为方程中的y，将示波器的A通道连接到结点①，B通道连接到结点②，就可以观察到x、y的时序图或x－y在二维相平面上的轨迹图。如果电路的输入信号源V1为正弦量

r从0到1取不同数值时的时序图和相轨道图与Matlab仿真结果类似:历经同宿轨迹、混沌轨迹、临界混沌状态、大尺度周期状态。特别地，当电源的有效值r=0.52556171 V时，系统表现为临界混沌态，如图4(a)所示，如果信号的有效值增加0.00000001 V变为r=0.52556172 V时，电路就由混沌态变为大尺度周期态，如图4(b)所示;可见Duffing电路仍具有对初始条件的极端敏感性，具备在高频下检测微弱正弦信号的前提条件。实验中还发现Duffing电路也有不同于Matlab仿真结果的独特之处，其独特之处及主要原因分析如下:

图4 Dufffing电路的状态Fig.4 States of the circuit

1)由混沌态变为大尺度周期态临界阈值和Matlab数值仿真略有不同，分析其原因主要有两点:

①所采用的数值解法不同。一般情况下，Matlab采用变步长ode45数值算法，即变步长4、5阶Rung-Kutta-Felhberg方法［13－14］，它是 Matlab 中最常用的求解微分方程的命令;而Multisim中主要采用两种改良的牛顿拉夫逊算法(Newton-Raphson Algorithm):Gmin Stepping算法和 Source Stepping算法［11－12］，由于混沌系统的初值敏感性，算法不同结果也不同。

②Duffing方程的Matlab仿真是严格的纯数值仿真，而Duffing电路不是严格的Duffing方程。由于在Multisim仿真电路中采用了实际型号的真实器件，特别是运算放大器并非理想，其输入失调电压Vos，输入失调电流Ios，输入偏置电流Ibs对电路从混沌态到大尺度周期态的阈值电压都有影响，电路的临界阈值 (幅值)为0.74325649 V，比Matlab求得的临界阈值0.73111185 V略大［15］，分析其原因主要是因为运算放大器的开环放大倍数不是∞，造成运算放大器的闭环增益要比设计值略小，使得电源需要稍大一点的幅值才能使电路进入大尺度周期态。

2)电路具有过渡过程:电路初始响应阶段有过渡过程，电压u1的初始响应如图5所示。图5中过渡过程很短，大约持续50 μs，类似于周期状态，该过程在相图中表现如图4(a)所示。相图外围的“环”即是过渡过程。随着r的增大“环”逐渐增大，当电路处于混沌临界态时，其最明显且最大。这在当前已有的研究资料中也没有见到。

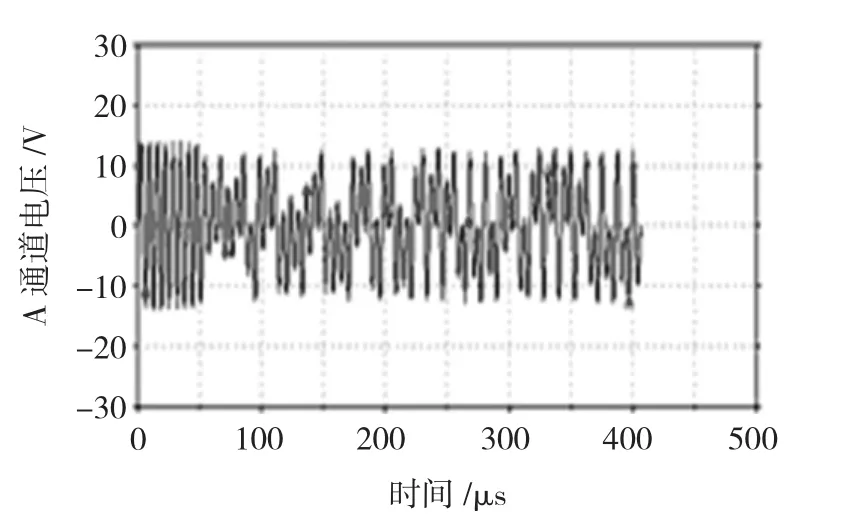
图5 电压u1的初始响应Fig.5 The initial response of u1

2.2 Duffing电路检测微弱信号性能的研究

首先调整Duffing电路使其处于混沌临界状态，确定临界阈值，然后对不同精确度临界阈值引入不同功率的热噪声并确定信噪比。这里采用Multisim器件库中现成的热噪声模块作为输入噪声，在一般检测系统的工作频率范围内可认为电热噪声是高斯白噪声，其均值为零。热噪声模块V12中有3个参数可设定，即带宽B、电阻值R和温度T，求信噪比时要计算噪声功率即方差σ2，σ2可由B、R和T求得，其计算方法如下［16－17］。

根据奈奎斯特给出的热噪声的功率谱密度函数为

算出热噪声模块的等效输出功率为

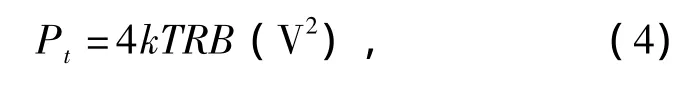
其中:k为波尔兹曼常数，k=1.38×10－23J/K;T为电阻的热力学温度，单位为K;R为电阻的阻值，单位为Ω;B为系统的等效噪声带宽，单位为Hz;

上式中的等效噪声带宽B可由系统的幅频特性近似确定，在工程允许的范围内B可近似用3 dB带宽来替代［17］。用Multisim对系统进行交流仿真可得系统的幅频特性，如图6所示，其纵坐标单位为dB。由图6可确定3 dB带宽大约为200kHz，因此不妨设定热噪声模块中的带宽B为200kHz，另外热噪声模块中的电阻温度一般取默认值为27℃，其热力学温度为

由式(4)可见，如果热噪声模块中B和T一定，调整R的数值就可得到不同功率的热噪声，然后据式(4)求出噪声功率后，确定信噪比，结果如表1所示。表1中临界阈值从0.5255开始，小数点后每增加一位有效位数，确定一次信噪比。例如，当r=0.5255 V时系统为混沌态，r=0.5256 V时系统处于大尺度周期态，设定r=0.5255 V为临界阈值，当被检测信号的有效值最小为A=0.5256－0.5255=10－4V时，系统由混沌跃变为大尺度周期态。然后加入热噪声模块(图3中的thermal noise)，逐渐增加热噪声功率σ2，仿真实验表明只要噪声的功率σ2不超过3.312×10－9，其对系统的状态和相变均无影响，这时最小信噪比［3］可确定为

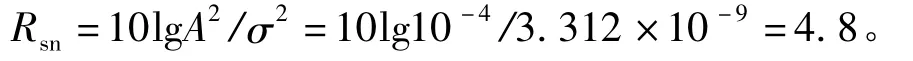
以此类推，可求得不同检测精确度时，Duffing电路的信噪比。

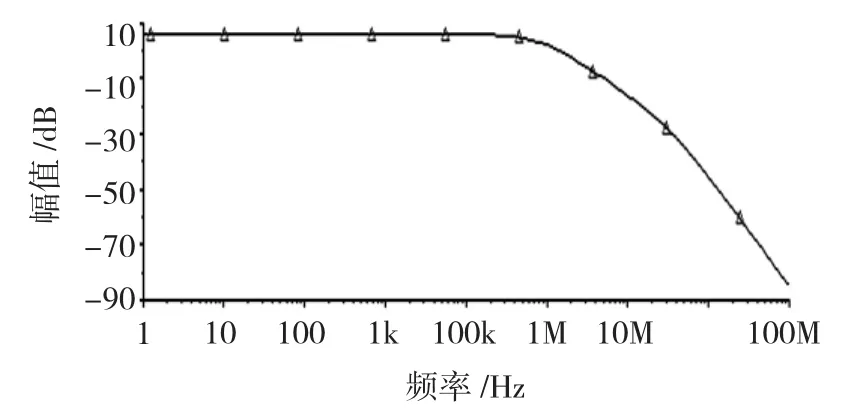
图6 Duffing电路的幅频特性Fig.6 Amplitude-frequency characteristic

表1 不同检测精确度时，Duffing电路的信噪比Table 1 When the detection accuracy is changed，the SNR of the Duffing circuit

为了避免噪声的随机性给系统状态和相变带来误差，表中的实验结果均是多次(大于10次)仿真后的结果。实验中发现一个新的现象:随着检测精确度的增加，信噪比在不断降低，如表1所示。这在以往的研究资料中没有见到。该现象可解释为:由于混沌系统对初值的敏感性，信号越微弱，电路对信号越敏感，其相应的抗噪声能力就越强。其更为深入的混沌学理论证明有待进一步研究。

3 结语

本文讨论了较高频率下Duffing电路的实现问题，改进了以往Duffing混沌电路只适合低频率检测的不足，该电路在运算放大器性能足够好的情况下，通过适当调节参数可实现从低频到高频的宽频带检测。通过对该电路的Multisim仿真，研究了Duffing电路在较高频率下的特性，仿真结果表明:在较高频率下，系统仍具有对初始值的敏感性和从混沌到大尺度周期态的临界相变，可用于较高频率下的微弱信号检测。通过加入热噪声模块，对Duffing电路的抗噪声能力进行了进一步的深入研究，研究和理论分析表明:Duffing电路可用于一定噪声强度下的微弱正弦信号检测。并发现随着检测精确度的增加，信噪比越来越低的新现象。

［1］李月，徐凯，杨宝俊，等.混沌振子系统周期解几何特征分析与微弱周期信号的定量检测［J］.物理学报，2008，57(6):3353－3358.LI Yue，XU Kai，YANG Baojun，et al.Analysis of the geometric characteristic quantity of the periodic solutions of the chaotic oscillator system and the quantitative detection of weak periodic signal［J］.Acta Physica Sinica，2008，57(6):3353 －3358.

［2］ZHANG Siyi，GAO Hongxia，LI Yaan，et al.A new method for detecting line spectrum of ship-radiated noise using Duffing oscillator［J］.Chinese Science Bulletin，2007，52(14):1906 －1912.

［3］王永生，姜文治，赵建军，等.一种Duffing弱信号检测新方法及仿真研究［J］.物理学报，2008，57(4):2053－2059.WANG Yongsheng，JIANG Wenzhi，ZHAO Jianjun，et al.A new method of weak signal detection using Duffing oscillator and its simulation research［J］.Acta Physica Sinica，2008，57(4):2053－2059.

［4］聂春燕，石要武.基于混沌检测弱信号的混沌特性判别方法的研究［J］.计量学报，2000，21(4):308－313.NIE Chunyan，SHI Yaowu.Research of identifying chaotic nature based on chaos to detecting weak signal［J］.Acta Metrologica Sinica，2000，21(4):308－313.

［5］王永生，肖子才，孙瑾，等.Duffing混沌系统电路仿真研究［J］.电路与系统学报，2008，13(1):133－135.WANG Yongsheng，XIAO Zicai，SUN Jin，et al.Simulation and experimental study on the chaos circuit of Duffing oscillator［J］.Journal of Circuit and System，2008，13(1):133－135.

［6］李月，杨宝俊.混沌振子系统(L－Y)与检测［M］.北京:科学出版社，2007:175－177.

［7］高继坤，杨焕明.运算放大器应用分析［M］.北京:北京理工大学出版社，1989:87－89.

［8］李哲英，骆丽.电子技术及其应用基础［M］.北京:高等教育出版社，2003:51－53.

［9］孔有林.集成运算放大器及其应用［M］.北京:人民邮电出版社，1988:321－332.

［10］钱国飞.集成运算放大器基本原理及应用［M］.北京:清华大学出版社，1984:22.

［11］熊伟，侯传教.Mutisim7电路设计及仿真应用［M］.上海:上海交通大学出版社，2005:71－72.

［12］从宏寿，程为群.Multisim8仿真与应用实例开发［M］.北京:清华大学出版社，2007:22.

［13］姜健飞.数值分析及其Matlab实验［M］.北京:科学出版社，2004:150－152.

［14］薛定宇，陈阳泉.高等应用数学问题的Matlab求解［M］.北京:清华大学出版社，2008:221－223.

［15］HU Wenjing，LIU Zhizhen.Study of metal detection based on chaotic theory［C］//8th World Congress on Intelligent Control and Automation，July 6 －9，2010，Jinan，China.2010:2309－2314.

［16］高晋占.微弱信号检测［M］.北京:清华大学出版社，2004:41－45.

［17］周求湛.弱信号检测与估计［M］.北京:北京航空航天大学出版社，2007:12－16.