基于RVM回归的姿控系统多故障检测

胡迪， 董云峰

(北京航空航天大学宇航学院，北京 100191)

0 引言

卫星姿控系统是保证卫星平台正常运行的重要系统之一。一般来说，卫星姿态控制系统由敏感器、执行机构以及姿控中心计算机组成，敏感器有很多种，如地球敏感器、陀螺和星敏感器等，执行机构一般有反作用轮、推力器和磁力矩器等，姿控中心计算机一般采用主备份冗余结构实现。当一个或多个敏感器/执行机构发生故障后，会对卫星姿控系统造成重大影响，轻则影响控制精确度，重则导致整星失效。由于姿控系统部件众多，其故障发生情况往往是多种故障的耦合效应。因此对卫星敏感器和执行机构的单一故障以及多发性或并发性故障进行诊断具有重要意义。

故障诊断是判定故障发生的位置和大小，而故障检测是故障诊断的第一步。

对于航天器来说，一般采用基于模型的方法进行故障诊断，如采用建模的方法［1］实现对飞船推进系统的故障诊断，或者采用观测器［2－3］实现对飞轮故障的检测和恢复等。通过数学建模的方法实现航天器故障诊断，受限于建模的精确度，并且不确定因素会导致误判，而通过基于信号处理和知识的方法［4］进行在轨故障诊断，往往受限于星载计算机的性能。

为了有效避免数学建模的误差，目前有学者提出通过对卫星在轨运行数据采集，采用最小二乘回归支持向量机(least square support vector regression，LSSVR)进行模型辨识，实现对部件的离线建模。同时通过在轨数据的离线建模也可以有效实现对干扰的估计建模。文献［5］采用LSSVR对姿控系统测量部件进行建模，通过求解半正定规划(semi－definite programming，SDP)问题来优化支持向量回归(support vector regression，SVR)的核空间，并验证了该方法具有很高的建模精确度，但其假定系统只有测量系统故障，没有考虑到执行机构系统也会发生故障的情况。文献［6］采用LSSVR对姿控测量系统建立观测器，从而可以检测故障，虽然考虑了不确定因素，但其依然受建模的精确度影响，并且采用LSSVR进行模型辨识或建立观测器，需要调节LSSVR模型的参数，其对辨识结果的精确度影响非常大。

目前学者针对某一部件失效后进行故障检测和诊断，如采用滤波器的方法［7］或神经网络的方法［8］实现对推力器的故障诊断，采用建立动态神经网络观测器的方法实现飞轮的故障检测［4］，采用无迹卡曼滤波(unscented kalman filtering，UKF)等方法实现姿态确定系统的故障诊断［9］等。

考虑到卫星姿控系统各个部件均可能发生故障，本文通过对各个部件的历史数据流向分析，采用相关向量机(relevance vector machine，RVM)分别对敏感器和执行机构进行回归辨识，离线建立辨识模型，在轨运行后通过部件输出与辨识模型输出产生残差，并进行评价，从而实现姿控系统的多故障检测。

1 系统描述

考虑如下姿态控制系统非线性状态方程［6］，即

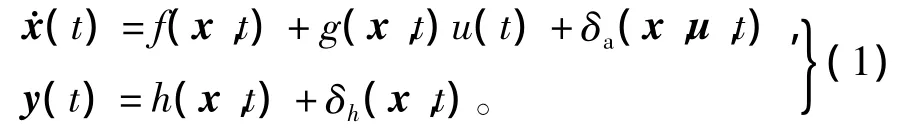
式中:x(t)∈Rn为系统的状态向量;u(t)∈Rm为系统的控制力矩输入向量;f(x，t)和g(x，t)的定义可参考文献［6］;δa(x，u，t)为执行机构故障;δh(x，t)为测量系统故障;h(x，t)为状态向量的测量函数。

考虑每个执行机构和测量部件有不同的故障模式，并且故障发生情况具有多发性和并发性的特点，即在同一时间内或同一时刻可能发生两种或两种以上的故障，因而对于某个部件发生故障后，需要检测出哪个部件发生故障，然后才能进行某个部件单机的故障诊断，本文通过引入相关向量机建模实现姿控系统多故障检测。

2 基于RVM的回归建模

相关向量机是［10－12］基于稀疏贝叶斯学习(sparse bayesian learning，SBL)方法，将高斯过程的贝叶斯推理方法应用到支持向量机中，通过类似于支持向量机(support vector machine，SVM)核转化的线性参数估计的方法，得到概率分布的结果。他具有SVM的特点，并且扩展了核函数的要求，使核函数不受Mercer条件的限制，因此可选核函数的范围更广，更适合于函数的回归。相关向量机回归参数的调节比SVM更少，性能比SVM更优，并且已经应用于机械轴承故障诊断［13］。

对于回归问题，即给定一系列输入和相应的输出，求解系统的模型问题。设输入样本为n维向量，某区域m个样本及其值表示为(x1，y1)，…，(xm，ym)∈Rn×Rm，则回归函数为

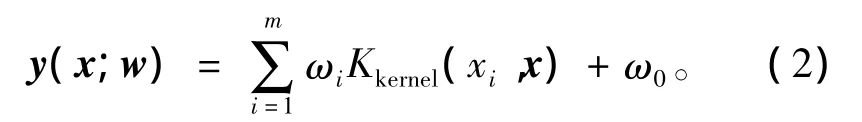
式中:x=［x1，x2，…，xm］为输入样本;w=［ω1，ω2…，ωm］T为权值;ω0为阀值;Kkernel(xi，x)为核函数。

对于新的输入x，通过回归函数预测输出y，而观测的输出则被认为是真实值受独立高斯噪声污染后的输出，即

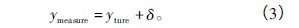
式中:δ为独立的附加高斯噪声，服从δ～N(yture，σ2)分布;ytrue为真实值;ymeasure为测量值，根据贝叶斯推理和独立性假设，可得标准似然函数为

式中:Ta=［δ1，δ2，…，δn］T;Φ 为 n ×m 阶矩阵，Φij=Kkernel(xi，xj)，i=1，2，…，n，j=1，2，…，m;K 为超参数的个数。

对于多权值的回归模型，其最大似然会得到过拟和的结果，而在相关向量回归模型中，通过使用Bayesian框架，使模型具有泛化性，参数的先验分布为

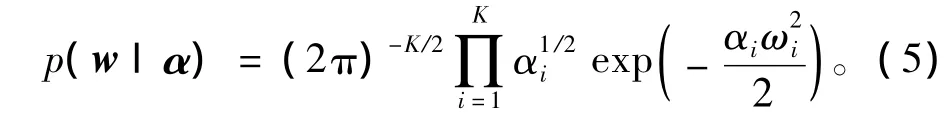
式中 α=［α1，α2，…，αK］为超参数。

在先验分布和似然分布的基础上，权值的后验分布可由Bayesian推理求得，得到其后验分布为

其中后验均值和方差分别为

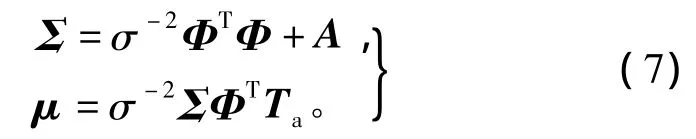
式中 A=diag(α1，α2，…，αK)。

在实际计算过程中，许多权值的后验分布趋于零，在相关向量机的回归模型中，非零的权值代表数据中的原型样本，这些称为“相关向量”。

式(3)中的目标输出似然分布可以通过对权值进行边缘积分求得，即

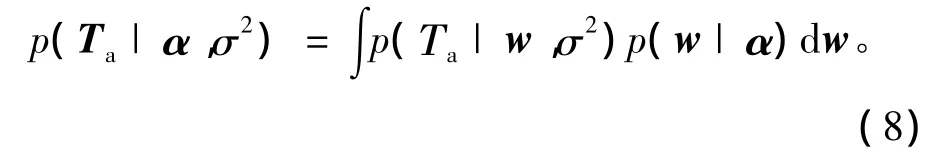
从而可得到超参数的边缘似然分布，即

式中 C=σ2I+ΦA－1ΦT，I为单位矩阵。

对于一组新的输入x*，其相应输出T*的预测分布满足高斯分布p(T*|Ta)～N(μ*)，其中

式中:F=［Φ1(x*)，Φ2(x*)，…，ΦK(x*)］T，Φi(x*)=Kkernel(x，x*)，i=1，2，…，K;为对式(4)的极大似然估计，决定了权重的最优值。

3 卫星姿控系统部件回归建模

建模精确度是基于模型的故障诊断方法的核心，通过建立精确的回归模型，可以有效实现故障检测及诊断。

本文在某高轨卫星正常模式下，采用地球敏感器(地敏)、太阳敏感器(太敏)和陀螺进行姿态确定，采用反作用轮进行姿态控制。考虑到地球敏感器和太阳敏感器的数据输入均为天体位置的矢量，因此本文仅考虑对太阳敏感器和陀螺的辨识建模。对于执行机构，本文考虑反作用轮辨识建模，可以推广到其他执行机构。

本文采用数学模型与辨识模型的差值表征辨识模型的精确性。

3.1 太阳敏感器回归建模

太阳敏感器分为数字式太阳敏感器和模拟式太阳敏感器，本文考虑数字式太阳敏感器，其根据太阳光线在码盘上的光照情况计算太阳光与测量狭缝间的夹角。

由于太阳敏感器需要知道太阳位置，而太阳位置计算与轨道卫星运行轨道相关，因此设定轨道根数集为:半长轴为42164 km;偏心率为零;轨道倾角为0°;升交点赤经为0°;近地点幅角为0°;真近点角为 30°。

考虑卫星数字太阳敏感器的其中之一安装在+X面，安装矩阵为

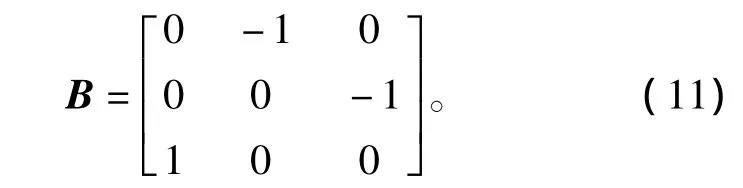
为正确辨识太阳敏感器的模型，需要对太阳敏感器的历史输入输出数据进行分析。太阳敏感器模型的输入为太阳矢量，输出为太阳敏感器测量角。卫星姿控系统正常运行600 s，提取前400 s数据用于训练模型，后200 s数据用于测试辨识模型是否正确。

分别采用LSSVR和RVM的建模误差对比如图1所示。

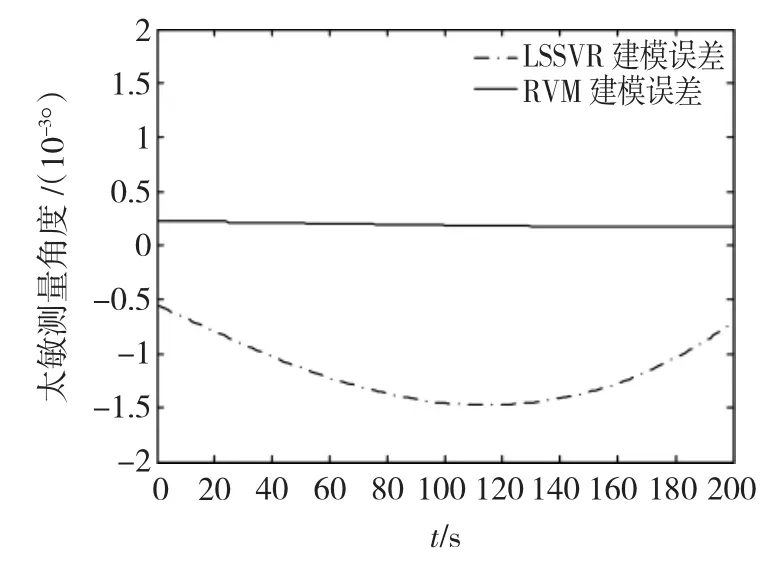
图1 太敏LSSVR和RVM建模误差对比Fig.1 Model error between LSSVR model and RVM model of digital sun sensor

由图1可知，二者建模误差均非常小。LSSVR辨识结果与LSSVR的参数调节有关，最大有0.0015°左右的差别，而RVM的辨识精确度比LSSVR高一个数量级，RVM辨识结果明显优于LSSVR辨识结果，可用于在轨故障诊断。

3.2 陀螺回归建模

考虑陀螺为3+1S陀螺组件，其中3个沿卫星三轴正交安装，S陀螺为斜装用于备份。本文在仿真时不考虑S轴陀螺。只考虑三轴正交安装的陀螺，每一个陀螺测量一个轴的角速度。

陀螺测量的是卫星相对于惯性姿态的角速度，卫星干扰存在时会对星体产生扰动，可通过陀螺反映出来。为了更为准确地表征陀螺的模型，将卫星动力学模型和陀螺本身模型一同考虑，因此陀螺建模时，其输入为反用轮的力矩指令，输出为星体的角速度。

卫星姿控系统正常运行600 s，前面400 s为模型训练，后200 s为模型测试。

分别采用LSSVR和RVM的建模误差对比如图2所示。

图2 陀螺LSSVR和RVM建模误差对比Fig.2 Model error between LSSVR model and RVM model of gyro

由图2可知，二者建模误差非常小，LSSVR的辨识结果比RVM要好，但可以看出，两者的辨识精确度都高达1 ×10－4°/s，最大差值也只有0.001°/s，因此可以忽略。利用RVM辨识模型能准确反映出陀螺的数据状态，可用于姿控系统故障诊断。

3.3 反作用轮回归建模

反作用轮沿三轴正交安装，整星为零动量系统。其中，斜装的反作用轮用于备份，此处不考虑。

反作用轮的输入为控制指令、电机电流，输出为反作用轮的转速，利用这3个信号可以进行模型辨识和建模。

分别采用LSSVR和RVM的建模误差对比如图3所示。

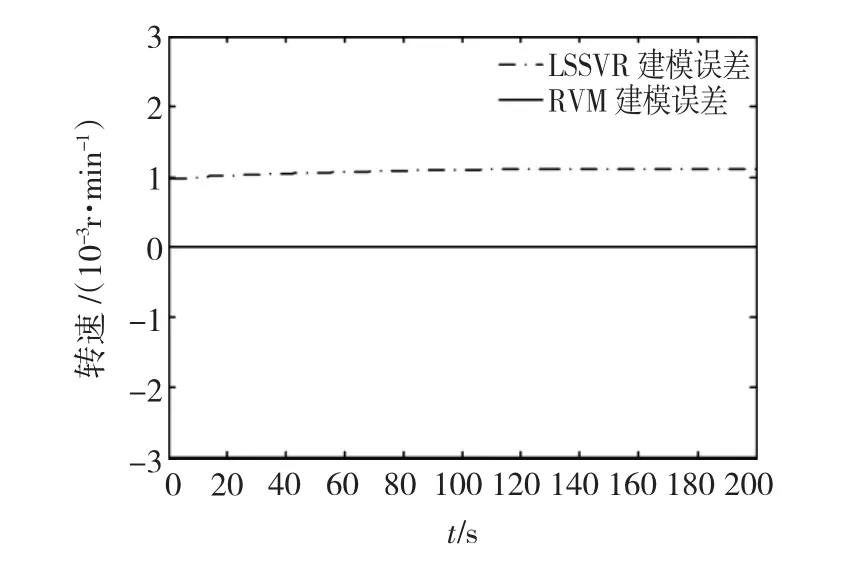
图3 反作用轮LSSVR和RVM建模误差对比Fig.3 Model error between LSSVR model and RVM model of reaction wheel

由图3可知，LSSVR辨识的模型与仿真模型的差值为0.001 r/min，而RVM辨识差值几乎等于零，因此RVM比LSSVR更能准确反映出反作用轮的工作状态，可以用于姿控系统故障诊断。

4 卫星姿控系统多故障检测

某同步轨道卫星在正常模式下，采用反作用轮进行姿态控制，采用太敏、地敏和陀螺进行姿态确定，因此整个姿控系统的故障检测即是对太敏、地敏、陀螺和反作用轮进行多故障检测。

由于卫星的故障具有并发性和多发性，在某一时刻陀螺和反作用轮可能会同时发生故障，或者在某一段时间内敏感器和执行机构同时发生故障，因此需对姿控系统进行多故障检测，用于区分敏感器故障和执行机构故障，检测完成后由各部件故障诊断算法完成某个部件的故障类型判定。

图4为某同步轨道卫星在正常模式下的系统级故障检测原理。利用上一节提出的RVM回归进行模型辨识后，将辨识模型加入姿控系统中，与部件输出数据形成残差，进而评价残差，从而实现故障诊断。

图4 卫星姿控系统故障诊断示意图Fig.4 The schematic of satellite attitude control system fault diagnosis

残差评价可采用残差加权平方和法，第k+1时刻的故障检测判别函数值L(k+1)［14］为

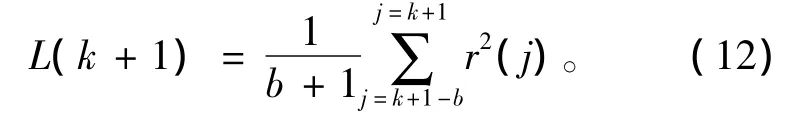
式中:b为选定的数据窗长度;r(j)为测量数据与辩识模型数据的残差。从而故障检测器可表示为

式中ε0为选定的检测门限值，此值应参考部件无故障时的残差选取。

5 仿真结果与讨论

利用MATLAB对姿控系统建模，根据正常数据对太阳敏感器、陀螺和反作用轮进行离线训练，并进行模型辨识，将辨识好的模型加入姿态控制系统。

为了反映卫星单一故障以及多发性和并发性故障，设计以下几种工况用于测试，分别为太敏故障、反作用轮故障、陀螺与反作用轮同一时间段发生故障以及太敏与反作用轮同一时刻发生故障。其中，太敏输出为太敏测量的角度，陀螺为Y轴陀螺输出的角速度，反作用轮为反作用轮A的转速。

5.1 太敏单一故障诊断

工况1，设定太敏在400 s时发生常值增大故障，陀螺和反作用轮正常，仿真结果如图5所示。

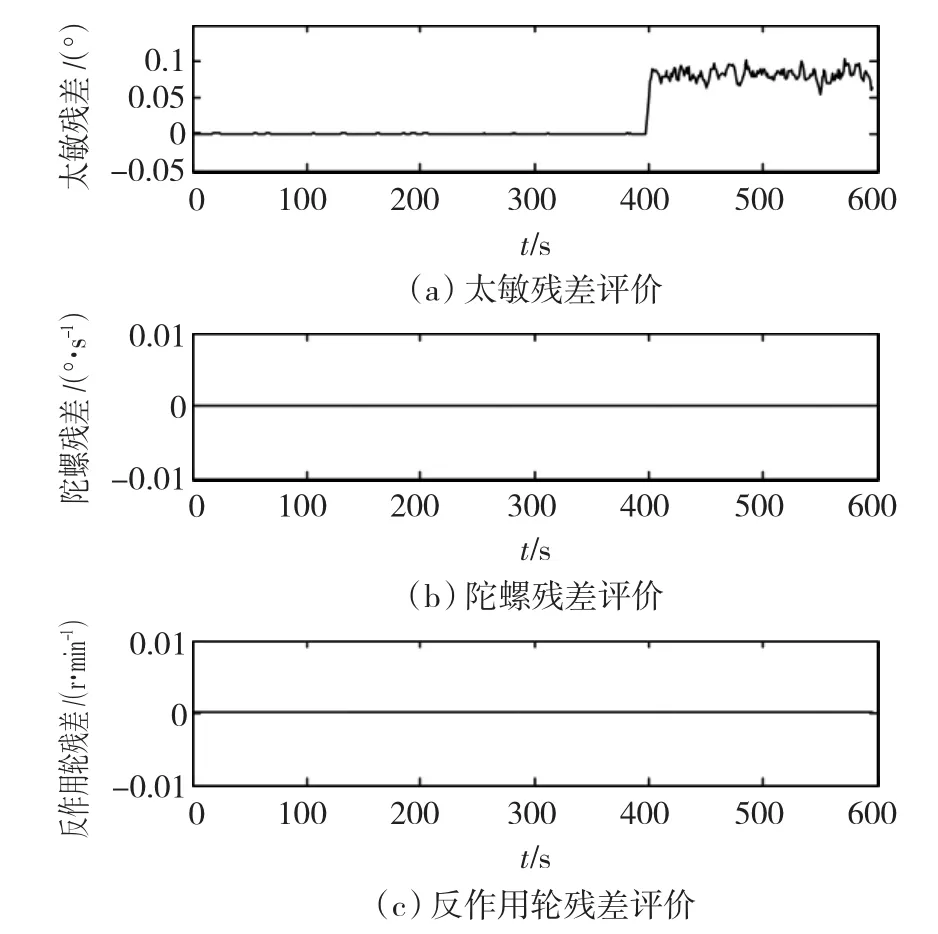
图5 工况1残差评价比较Fig.5 Residual evaluation of scenario 1

由残差评价可见，RVM和LSSVR均检测到太阳敏感器在400s时发生了故障，而陀螺和反作用轮没受到干扰，故障诊断结果与预设一致。

5.2 反作用轮A单一故障诊断

工况2，设定反作用轮在500 s时发生故障，沿X轴方向的反作用轮发生轴承卡死的故障，陀螺和太敏不发生故障，仿真结果如图6所示。

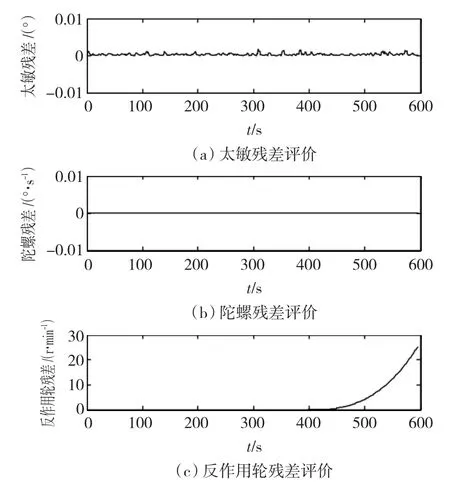
图6 工况2残差评价比较Fig.6 Residual evaluation of scenario 2

由图6可以知，在500 s时反作用轮A的转速残差发生了突变，表征有故障发生，而陀螺和太敏测量数据的残差没有发生变化，因此故障诊断结果也与预设值一样。

5.3 Y轴陀螺与反作用轮A多发性故障诊断

工况3，设定沿Y轴方向的陀螺在300 s时发生常值增大故障和沿X轴方向的反作用轮在400 s时发生摩擦力矩增大故障，仿真结果如图7所示。

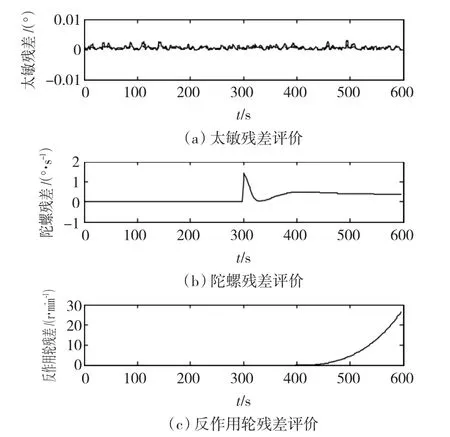
图7 工况3残差评价比较Fig.7 Residual evaluation of scenario 3

由图7可知，在300 s时Y轴陀螺发生故障，在400 s时反作用轮A发生故障，而太敏残差一直为零，因此故障判定与预设一致。

5.4 太敏与反作用轮A并发性故障诊断

工况4，假定太敏与反作用轮在400 s时同时发生故障，太敏发生常值增大故障，沿X轴方向的反作用轮故障为反电动势增大，仿真结果如图8所示。

图8 工况4残差评价Fig.8 Residual evaluation of scenario 4

由图8可知，在400 s时同时发生了两种故障，一种是太敏故障，一种是反作用轮故障。由残差评价也可知，通过RVM实现模型辨识，可以实现并发性故障诊断。

6 结语

本文通过RVM回归对卫星姿控系统的敏感器和执行机构进行离线回归建模，根据正常数据对辨识模型进行测试，在轨运行时考虑敏感器和执行机构均可能发生故障，采用辨识模型与仿真模型形成残差输出，通过加权平方和对残差进行评价，实现卫星姿控系统单一故障诊断和系统级故障诊断。仿真结果表明，RVM回归较LSSVR回归可以有效实现对部件进行回归建模，通过回归建模不仅可以实现在轨卫星姿控系统单一故障诊断，也可以实现并发性和多发性故障诊断，为单机故障诊断提供先决条件，降低故障诊断的错误率，提高在轨故障诊断的实时性。因此，该方法可用于工程实践中对部件模型进行辨识，从而实现故障诊断。

［1］宝音贺喜格，姜兴渭，黄文虎.基于模型的故障诊断方法在飞船推进系统中的应用［J］.推进技术，1999，20(4):5－8.BAOYAN Heshig，JIANG Xingwei，HUANG Wenhu.Application of model based fault diagnosis method to propulsion system of spacecraft［J］.Journal of propulsion technology.1999，20(4):5－8.

［2］田科丰，李智斌基于自适应观测器的飞轮故障诊断方法［J］.华中科技大学学报:自然科学版，2009，37(S1):184－186.TIAN Kefeng，LI Zhibin.Reaction wheel fault diagnosis based on adaptive observer［J］.Journal of Huazhong University of Science and Technology:Nature Science Edition，2009，37(S1):184－186.

［3］金磊，徐世杰.基于扩张状态观测器的飞轮故障检测与恢复［J］.北京航空航天大学学报，2008，34(11):1272－1275.JIN Lei，XU Shijie.Extendted state observer-based fault detection and recovery for flywheels［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(11):1272 －1275.

［4］LI Zhongqi，MA Liying，KHORASANI Khashayar.Fault detection in reaction wheel of a satellite using observer-based dynamic neural networks［J］.Lecture Notes in Computer Science，3498(3):584－590.

［5］赵石磊，张迎春.SVM回归估计方法在卫星故障诊断中的应用［J］.电机与控制学报，2008，12(4):483－486.ZHAO Shilei，ZHANG Yingchun.Application of SVM regression to fault diagnosis for satellite［J］.Electric Machines and Control，2008，12(4):483 －486.

［6］王剑非，姜斌，冒泽慧.基于LSSVM的卫星姿态控制系统故障诊断［J］.控制工程，2008，15(3):334－346.WANG Jianfei，JIANG Bin，MAO Zehui.LSSVM based fault diagnosis for satellite attitude control systems［J］.Control Engineering of China，2008，15(3):334 －346.

［7］HENRY D.Fault diagnosis of microscope satellite thrusters using H∞/H－filters［J］.Journal of guidance，control，and dynamics，2008，31(3):699－711.

［8］VALDES A，KHORASANI K.A pulsed plasma thruster fault detection and isolation strategy for formation flying of satellites［J］.Applied Soft Computing Journal，2010，10(3):746 －758.

［9］PIRMORADI F N，SASSANI F，DE SILVA C W.Fault detection and diagnosis in a spacecraft attitude determination system［J］.Acta Astronautica，2009，65(5 －6):710 －729.

［10］TIPPING Michael E.Bayesian inference:an introduction to principles and practice in machine learning［J］.Advanced lectures on machine learning，2006，3176:1－19.

［11］刘芳.基于小波分析和相关向量机的非线性径流预报模型研究［D］.武汉:华中科技大学控制科学与工程系，2007.

［12］TIPPING Michael E.Sparse bayesian learning and the relevance vector machine［J］.Journal of Machine Learning Reaserch，2001，1:211 －244.

［13］LEI Liangyu，ZHANG Qing.Relevance vector machine based bearing fault diagnosis［C］//2006 International Conference on Machine Learning and Cybernetics，August 13 － 16，2006，Dalian，China.2006:3492 －3496.

［14］刑琰，魏春岭.基于四元数估计角速率的陀螺故障定位［J］.宇航学报，2003，24(4):410－413.XING Yan，WEI Chunling.Fault location of single redundant gyroscopes based on estimated angular rate using quaternion ［J］.Journal of Astronautics，2003，24(4):410 －413.