Z源并网逆变器的间接单周电流控制策略

侯世英， 肖旭， 张闯， 黄哲

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

0 引言

随着现代社会对能源需求的不断增加，全球范围内的能源危机日益突出，研究基于可再生能源的分布式发电系统具有重要意义［1－5］。可再生能源发出的电能的电压等级一般较低，且存在较大的波动［6］，因此需在逆变前加入升压电路来提高逆变器直流侧的输入电压，但所加入的直流升压电路与逆变器构成两级拓扑结构，不仅降低了系统的效率，也增加了主电路的体积和成本。Z源逆变器［7］是一种可实现升压变换功能的单级式拓扑，利用其独特的无源网络还能使同一桥臂上的开关管可以同时导通，而不必插入死区时间，提高了并网电能质量及系统的稳定性，因此Z源逆变器在可再生能源发电领域受到广泛关注［8－11］。

目前，国内外对于并网逆变器的研究普遍采用电流控制策略［12］，即把逆变器控制成一个电流源，使其输出电流与电网电压同频同相。针对Z源并网逆变器的控制方式，国内外学者进行了大量研究，文献［13］提出一种改进型滞环电流控制方式，获得较好的输出效果，但控制系统中需要多个采样保持环节，使系统变得复杂，可靠性降低;文献［14］提出一种滑模控制方式，但其控制参数的整定非常复杂;文献［15］提出一种直接单周电流控制方式，其控制结构较为复杂，且其控制精确度依赖于电流检测环节的精确度，如果电流检测环节出现故障，将会对输出电能质量造成严重影响。

本文提出一种无需电流检测的间接单周电流控制方式，通过建立Z源并网逆变器的状态平均数学模型，根据状态平均法推导出实现逆变器输出电流与电网电压同频同相的占空比的控制函数d(t)，再利用单周控制的思想，根据d(t)产生相应的开关驱动信号，从而控制并网电流。该控制方式通过实时检测电网电压和直流侧输入电压的瞬时值作用于控制函数d(t)，在确保并网电流与电网电压同频同相的同时，有效抑制输入电压波动造成的干扰，输出电能质量良好，且该控制方式的基础是系统的状态平均模型，有别于传统的基于系统稳态数学模型的间接电流控制方式，有效地改善了传统间接电流控制方式的快速性。本文在理论分析的基础上搭建仿真模型来验证所提出的控制方式的正确性和有效性。

1 控制函数的推导

Z源并网逆变器的主电路如图1所示。其中，电感L1、L2与电容C1、C2构成阻抗网络，利用该阻抗网络可以保证逆变器在直通状态下不再使电源短路，并能提高逆变器直流输入端的电压。为了不影响输出电能质量，直通状态应加在逆变器原来的0状态上，因此逆变器并网运行时，在电网电压正半周会出现3个工作模态，其中非直通状态下有2个工作模态，如图2所示。

图1 单相Z源并网逆变器Fig.1 The single-phase Z source grid-connected inverter

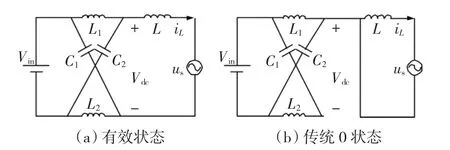
图2 Z源并网逆变器非直通工作状态Fig.2 The non shoot-through operation modes of Z source grid-connected inverter

由于阻抗网络上的电感L1、L2和电容器C1、C2分别具有相同的电感值L和电容值C，因此阻抗网络是一个对称网络，有

有效状态如图2(a)所示，开关S1和S4导通，S2和S3断开，二极管Din导通，有

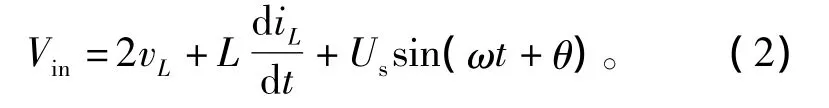
式中:Vin为直流侧输入电压;iL为滤波电感上的电流，即并网电流;Us为电网电压的幅值;ω为角频率;θ为相角。该状态下阻抗网络电感上的电压vL为

将式(3)代入式(2)可得

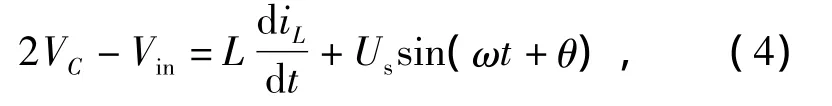
将式(4)定义为有效状态的状态方程。

传统的0状态如图2(b)所示，开关S1和S2导通，S3和S4关断，二极管Din导通，有

式(5)为0状态的状态方程，此时阻抗网络电感上的电压vL仍为Vin－VC，与有效状态时的电压相同。

Z源并网逆变器的直通状态如图3所示，开关S1、S2、S3、S4均导通，二极管 Din截止，逆变器处于直通状态。由于直通状态是加在传统的0状态上，其状态方程仍与式(5)相同，但此时阻抗网络电感上的电压vL为

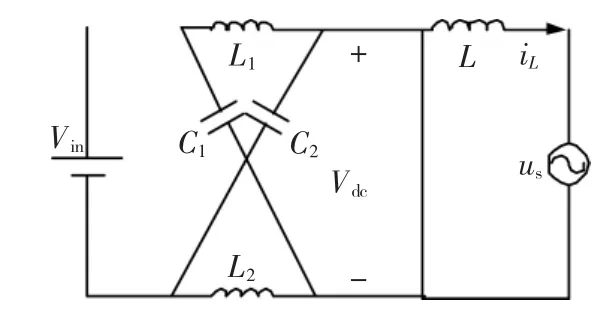
图3 Z源并网逆变器直通工作状态Fig.3 The shoot-through operation modes of Z source grid-connected inverter

若令直通占空比为D0，那么根据阻抗网络上电感L1或L2的伏秒平衡关系可得

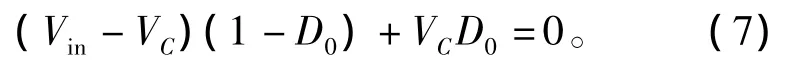
整理上式可得

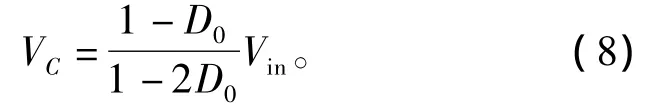
将式(8)代入式(4)，则有效状态的状态方程为

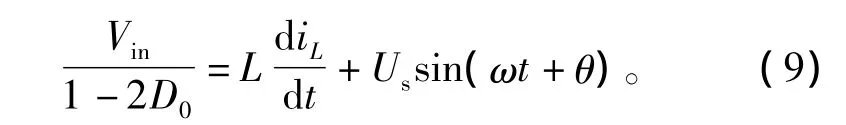
由以上分析可知，在不考虑直通状态的情况下，在电网电压的正半周，开关管S1一直导通，S2、S4互补导通。当考虑到直通状态时，直通状态加在传统的0状态上，因此设开关S4工作于有效状态的占空比为d(t)，直通占空比D0≤1－d(t)。那么在一个开关周期Ts内，有效状态持续的时间为d(t)Ts，传统的0状态的持续时间则为［1－D0－d(t)］Ts，直通状态的持续时间则为D0Ts。当电网电压处于负半周时，可做类似分析，不再赘述。于是可以得到系统的状态方程为

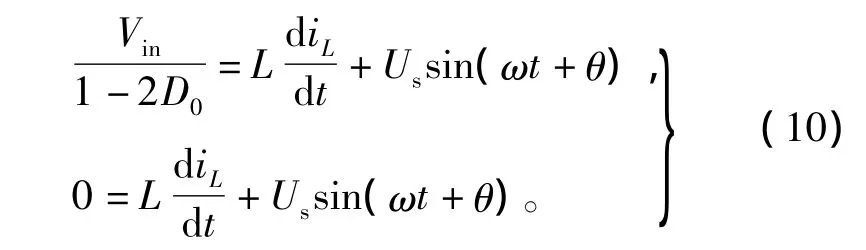
基于状态平均法的思想，由式(10)可得单相Z源并网逆变器的状态平均方程为

为了保证并网逆变器的输出电流与电网电压同频同相，那么令滤波电感平均电流为

式中:IL为并网电流的幅值，其大小由可再生能源发出的有功功率来决定。式(12)为该控制方式下的目标函数，将目标函数代入式(11)整理可得占空比d(t)为

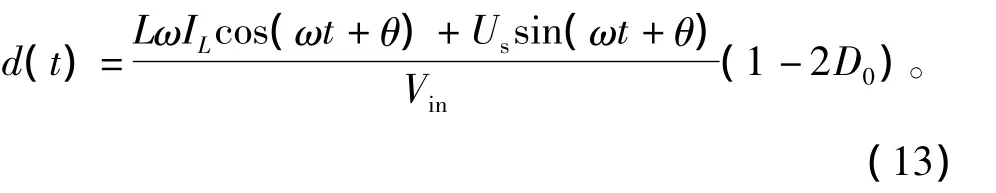
式中ω、Us、θ和Vin为电网电压和直流侧输入电压的实时检测量，通过这4个量可以有效地反映电网电压和直流源的瞬时状态，因此，控制系统能够根据输入电压的变化及电网电压的波动自动生成相应的占空比d(t)，从而保证系统具有很好的抗干扰能力，提高了系统的鲁棒性。

2 间接单周电流控制策略

控制电路结构如图4所示，主要包含占空比计算单元、复位积分器、R－S触发器、比较器、开关选择单元、逻辑比较电路、直通脉冲发生器。通过外部检测单元实时检测到的直流侧电压Vin，交流侧电压的特征量ω、Us、θ，并网电流幅值 IL及直通占空比D0，按式(12)实时计算占空比控制函数d(t)。由于积分器输出始终为正，对于电网电压处于负半周时的d(t)应取绝对值，因此将d(t)信号通过绝对值单元得到实现单位功率因数并网的占空比参考信号dref。

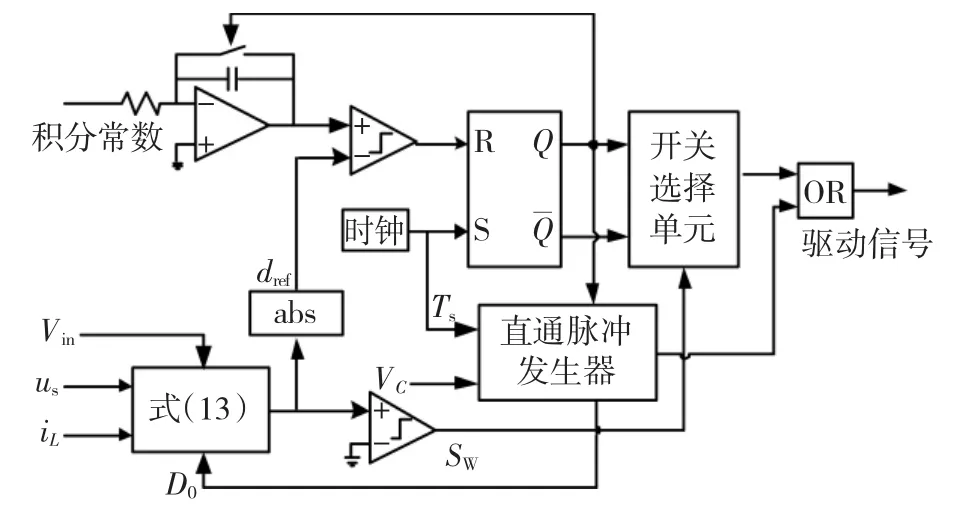
图4 控制电路结构Fig.4 The structure of the control circuit

将占空比参考信号dref与复位积分器的输出信号进行比较，积分常数选为与R－S触发器时钟脉冲的频率fs相等的常数。当积分器输出信号小于dref，R－S触发器保持原状态，逆变器工作于有效状态;而当积分器输出大于dref时，使R－S触发器复位，逆变器进入0状态，通过R－S触发器Q端电平的跳变，触发直通脉冲发生器，保证直通状态加在0状态上，直通脉冲发生器结构如图5(a)所示。由于Z源并网逆变器的电容电压必须高于电网电压的峰值，逆变器才能正常工作，按照此规则设定阻抗网络电容电压的参考值Vcref，将其与实际检测的电容电压VC的误差经过PI调节器，得到直通占空比D0，再与开关周期相乘，即得到直通脉冲时间，再通过脉冲发生器产生触发脉冲。为了不影响输出电能质量，直通脉冲应加在0状态上，因此通过检测R－S触发器复位时Q端的下降沿触发直通脉冲发生器，然后输出指定时间的直通脉冲。在如图5(b)所示的开关选择单元中，将直通脉冲与R－S触发器的输出量取或运算，最后由控制信号Sw决定开关信号的逻辑组成，得到Z源并网逆变器的开关驱动信号。

图5 控制电路内部结构Fig.5 The internal structure of the control circuit

本文以Sw=1(电网电压的正半周期)为例，说明控制电路的工作过程，在时钟脉冲到来时，R－S触发器Q端输出高电平，¯Q端输出低电平，此时开关S1、S4导通，同时积分器以积分常数fs开始积分，在积分器的输出信号小于占空比的参考值dref的过程中，触发器的复位端一直处于低电平，R－S触发器的状态保持不变，逆变器工作于有效状态;当积分器输出大于占空比参考信号dref时，比较器输出高电平，将R－S触发器复位，则Q端输出低电平，¯Q端输出高电平，并将积分器复位，结束积分过程。逆变器本应进入传统的0状态，而直通脉冲发生器检测到Q端由高到低变化时产生的下降沿，产生设定时间T0的直通脉冲，由于直通脉冲与R－S触发器输出信号是做或运算，此时所有开关均导通，直到直通时间结束，逆变器才进入传统的0状态，开关S1、S2导通。此状态一直维持到下一个时钟到来时结束，待下一个时钟到来时，又开始一个新的积分过程。

3 仿真验证

为了验证所提出的Z源并网逆变器间接单周控制方式的正确性及其工作性能，建立仿真模型并进行仿真分析。电路参数为:直流输入电压Vin=300 V;阻抗网络电感 L1=L2=1000 μH;电容C1=C2=470μF;电网电压的有效值为220 V;频率为50 Hz;相角θ=0°;滤波电感L=1 mH;R－S触发器时钟脉冲频率fs=10kHz;输出功率Pout=4 kW。

当设定阻抗网络电容电压Vcref=338 V，即直通占空比D0=0.1时，Z源逆变器的输出波形如图6所示。由图6可知，并网电流与电网电压保持同频同相，且并网电流大小满足输出功率要求，实现了以单位功率因数并网;另外由VC和Vdc波形可知，在启动过程中，电容电压在经过不到2个工频周期可以达到稳态，超调量也较小，且启动时电容上的冲击电压非常小，由此可知在该控制方式下，系统具有良好的启动特性，且输出电能质量良好。通过对并网电流iL进行频谱分析可知并网电流的总谐波畸变率(total harmonic distortion，THD)为1.22%，其频谱如图7所示。

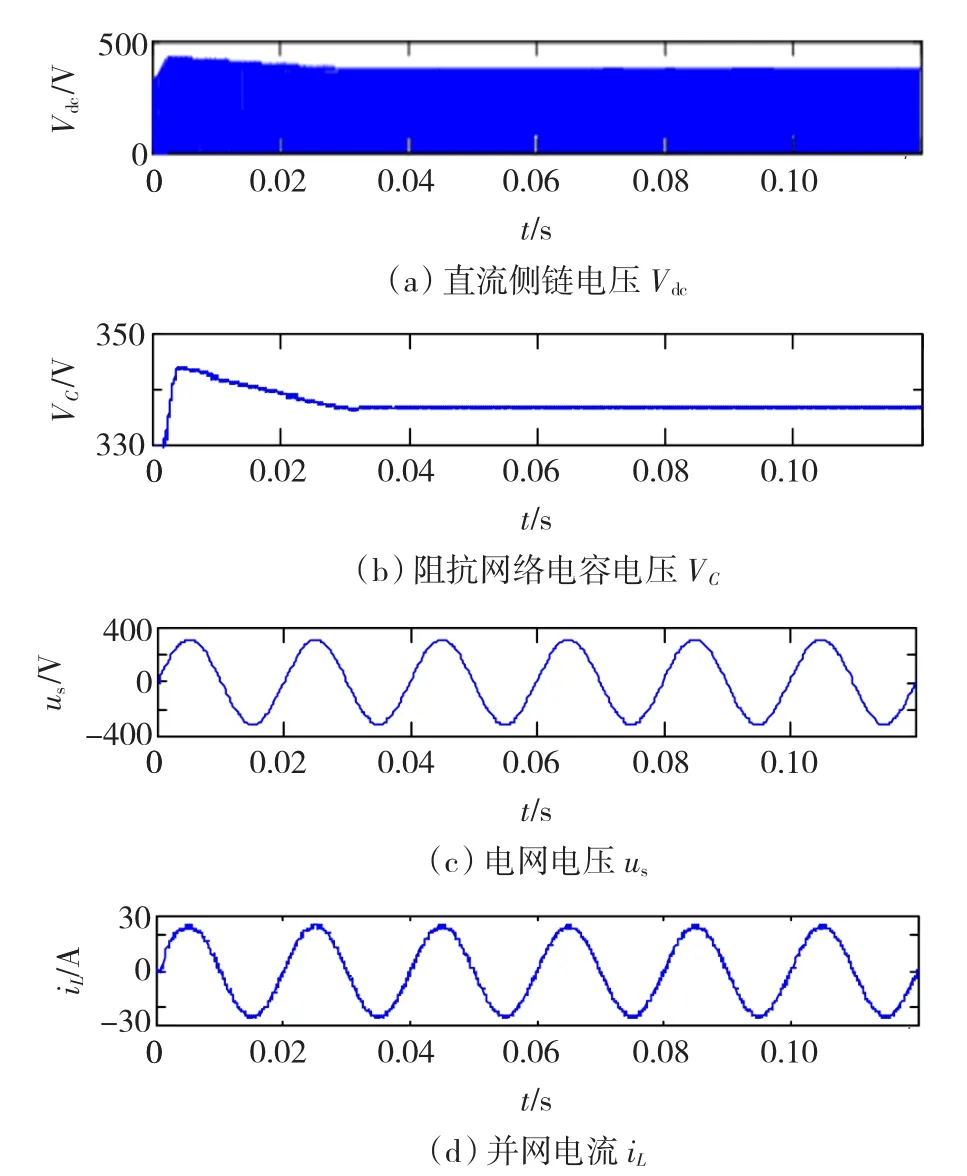
图6 Z源并网逆变器输出波形Fig.6 Output waveform of the Z source grid-connected inverter

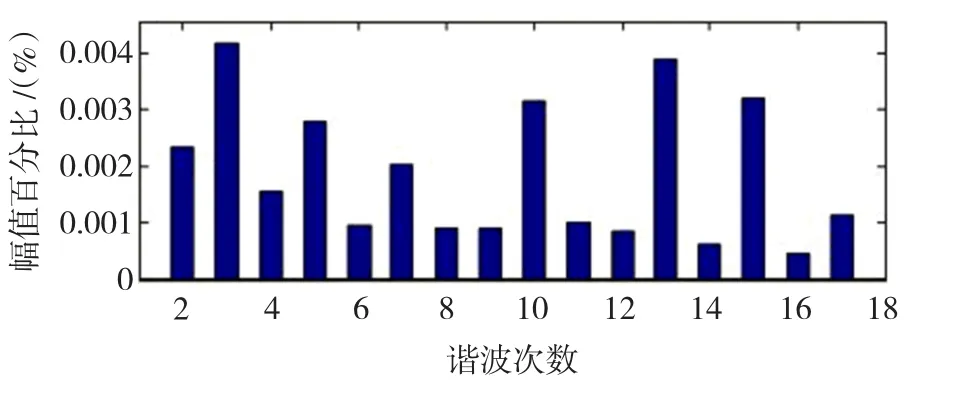
图7 并网电流iL频谱Fig.7 The frequency spectrum of the grid current

图8为直流侧输入电压Vin突变时Z源并网逆变器输出波形，在0.09 s时，直流电压Vin=280 V，并伴随10 V的波动信号。从图8中可以看出，并网电流iL几乎不受影响，电容电压在经过0.02 s的小幅波动后随即进入稳态，继续稳定在338 V。

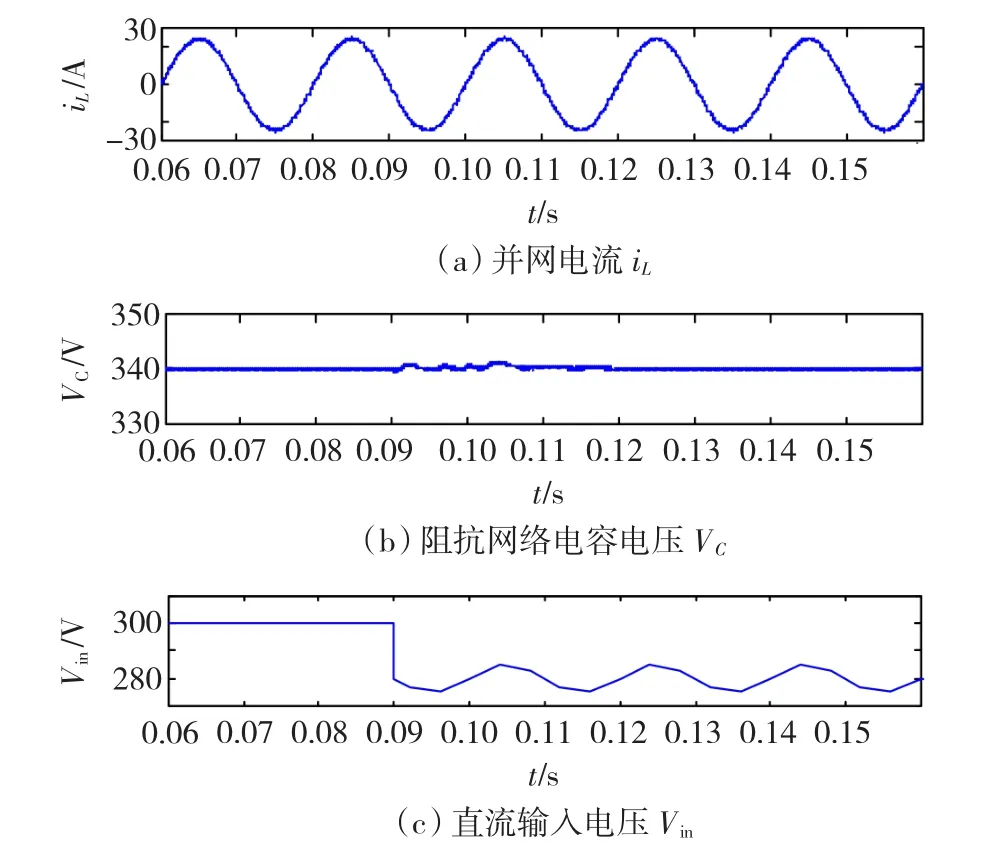
图8 直流输入电压突变时的输出波形Fig.8 The output waveform of the inverter when the input voltage suddenly changes

图9为当直流输入电压同为280 V，需并入有效值为220 V的电网时，Z源逆变器与传统电压型逆变器并网电流波形的对比。由于直流输入电压280 V小于电网峰值电压311 V，传统的电压型逆变器的并网电流出现了严重的畸变，如图9(a)所示。而Z源逆变器由于其具有升压变换功能，在输入电压较低时仍能维持良好的输出电能质量，如图9(b)所示。

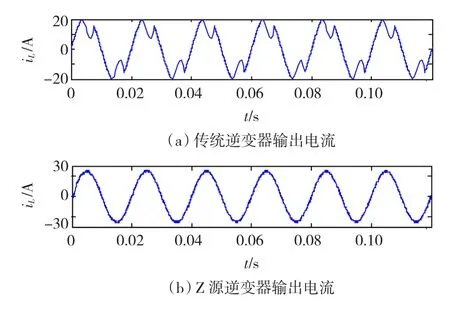
图9 直流输入电压为280 V时的输出电流波形Fig.9 The output current waveform when the DC input voltage is 280 V

图10为改变输出功率时的Z源并网逆变器输出电流波形，从图10中可以看出，并网电流能够迅速按指令变化并且达到稳态，由此可知系统的动态特性和稳态特性均较好。

图10 改变参考值后的电流波形Fig.10 The current waveform after changing the reference value

4 结语

本文提出一种用于Z源并网逆变器的间接单周电流控制方式。该控制方式的特点是无需电流检测环节，使控制结构十分简单，降低了控制成本。由于本控制方案是基于系统的状态平均模型而建立的，解决了传统的间接电流控制动态特性差的问题，同时结合单周控制，使系统具有良好的鲁棒性，能够及时对电压波动做出反应，理论分析与仿真结果验证了上述结论。这种控制策略实现方法简单，在中、小型功率的可再生能源发电并网中有一定的实用价值。

［1］HO B M T，CHUNG Shuhung.An integrated inverter with maximum power tracking for grid － corrected PV systems［J］.IEEE Transactions on Power Electronics，2005，20(4):953 －962.

［2］李立，黄松柏，汪洪亮.基于电压/电流控制模式的组合式三相逆变器［J］.电机与控制学报，2011，15(2):63 －70.LI Li，HUANG Songbai，WANG Hongliang.Combined three phase inverter operating in voltage or current control mode［J］.E-lectric Machines and Control，2011，15(2):63 －70.

［3］PRASAD B S，JAIN S，AGARWAL V.Universal single-stage grid-connected inverter［J］.IEEE Transactions on Energy Conversion，2008，23(1):128－137.

［4］HOLLAND Kent，PENG Fang Z.Control strategy for fuel cell vehicle traction drive systems using the Z-source inverter［C］//2005 IEEE Vehicle Power and Propulsion Conference，September 7 －9，2005，Chicago，USA.2005:639 －944.

［5］戴训江，晁勤.一种新颖的并网逆变器自适应电流滞环控制策略［J］.电力自动化设备，2009，29(9):85 －89.DAI Xunjiang，CHAO Qin.Adaptive current hysteresis control of grid － connected inverter［J］.Electric Power Automation Equipment，2009，29(9):85 －89.

［6］XUE Yaosuo，CHANG Liuchen，KJAER S B，et al.Topologies of single-phase inverters for small distributed power generators:an overview［J］.IEEE Transactions on Power Electronics，2004，19(5):1305－1314.

［7］彭方正，房绪鹏，顾斌，等.Z源变换器［J］.电工技术学报，2004，19(2):47 －51.PENG Fangzheng，FANG Xupeng，GU Bin，et al.Z-source converter［J］.Transactions of China Electrotechnical Society，2004，19(2):47－51.

［8］PARK Jong Hyoung，KIM Heung Geun，NHO Eui Cheol，et al.Grid-connected PV system using a quasi-Z-source inverter［C］//24th Annual IEEE Applied Power Electronics Conference and Exposition，APEC 2009，February 15 － 19，2009，Washington，USA.2009:925－929.

［9］王继东，朱雪玲，苏海滨.三相光伏并网Z－源逆变器的比例谐振控制［J］.电机与控制学报，2010，14(4):86 －91.WANG Jidong，ZHU Xueling，SU Haibin.Proportional－resonant control for Z-source inverter in three-phase PV grid-connected system［J］.Electric Machines and Control，2010，14(4):86 － 91.

［10］LOH Poh Chiang，GAJANAYAKE Chandana Jayampathi，VILATHGAMUWA D Mahinda， et al.Evaluation of resonant damping techniques for Z-source current － type inverter［J］.IEEE Transactions on Power Electronics，2008，23(4):2035 －2043.

［11］LIU Jingbo，HU Jiangang，XU Longya.Dynamic modeling and analysis of Z-source converter:derivation of AC small signal model and design-oriented analysis［J］.IEEE Transactions on Power Electronics，2007，22(5):1786 －1796.

［12］顾和荣，杨子龙，邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究［J］.中国电机工程学报，2006，26(9):108－112.GU Herong，YANG Zilong，WU Weiyang.Research on hysteresis-band current tracking control of grid-connected inverter［J］.Proceedings of the CSEE，2006，26(9):108－112.

［13］郑建勇，黄金军，尤鋆，等.基于电流滞环控制的Z源光伏并网系统研究［J］电机与控制学报，2010，14(5):61－67.ZHENG Jianyong，HUANG Jinjun，YOU Jun，et al.Research on Z source based current hysteresis control used in photovoltaic grid-connected system［J］，Electric Machines and Control，2010，14(5):61－67.

［14］陈宗祥，蒋赢，潘俊民，等基于滑模控制的Z源逆变器在单相光伏系统中的应用［J］.中国电机工程学报，2008，28(21):33－39.CHEN Zongxiang，JIANG Ying，PAN Junmin，et al.A Z-source inverter for a single-phase PV system based on sliding-mode control［J］.Proceedings of the CSEE，2008，22(21):33 －39.

［15］蒋立，郑建勇.Z源光伏并网直接电流单周控制系统［J］.电力系统自动化，2008，32(22):87 －90.JIANG Li，ZHENG Jianyong.A direct current one-cycle control method for Z-source grid-connected photovoltaic system［J］.Automation of Electric Power Systems，2008，32(22):87 －90.