基于流体传热理论永磁风力发电机温度场计算

李伟力， 袁世鹏， 霍菲阳， 张奕黄

(1.北京交通大学电气工程学院，北京 100044;2.哈尔滨理工大学电气与电子工程学院，黑龙江 哈尔滨 150080)

0 引言

风能作为清洁的可再生能源为人们所关注，风力发电技术也逐步成熟。随着对风力发电电机性能和成本的双重要求提高，电机的功率密度越来越大，电磁负荷和热负荷也越来越高，故温升也成为电机设计中需要考虑的问题［1－7］。特别是对于大功率永磁同步发电机，温升过高会使永磁体的磁通密度下降，影响电机性能的稳定，甚至会导致永磁体的不可逆退磁，故电机温度场计算尤为重要。

对于流体、传热等问题的分析，有限体积法有其独特的优势。有限体积法得出的离散方程，要求因变量的积分守恒对任意一组控制体积都要满足。

所以在电机温升计算中，有限体积法也渐渐为研究者所重视［8－12］。

在传统的研究方法中，大都把电机外环境的流场风速视为一个常数，而相对应的表面散热系数也视为常数，但没有将流动和传热过程进行耦合计算，给计算带来很大的偏差［8－9］。

本文在流体力学理论、传热学理论和有限体积法的基础上，首先，确定发电机热源及等效导热系数的计算方法，以及电机表面自然风的紊流模型。其次，计算了一台表面风冷式小型风力发电机的三维温度场，并通过与实验结果的对比，验证了该电机温度场计算模型的合理性。最后，利用相同方法对一台1.5 MW永磁同步风力发电机的三维温度场进行计算与分析，在此基础上，根据大功率永磁风力发电机的实际特点，仿真计算了在不同环境温度下以及不同风速状况下发电机的温度分布。

1 电机热性能参数的确定

对于全封闭表面风冷式结构电机，其内部无通风冷却系统，定子绕组内热量散热主要是经定子铁心由机壳传递给周围的空气和由铁心向气隙内放热。为了方便分析电机传热过程，可对电机内部条件作相应的假设和归算，这对建模和有限元分析具有很大的帮助。

1.1 热源的确定

电机运行过程中，必然要产生相应的损耗，这些损耗转换成热，通过电机各部件与周围环境进行热交换，最终达到热平衡。准确计算电机各部分损耗是准确计算电机温度场的前提。

半直驱风力发电机以同步转速旋转，主磁场在转子铁心的交变频率很低，转子铁耗非常小;且由于电机转速很低、频率低，无集电环、无通风系统、无阻尼绕组，故机械损耗与杂散损耗非常小，相对于铜耗与基本铁耗近似可以忽略。

通过设计值或实验值确定定子绕组铜耗。利用场路耦合方法计算定子各部位铁耗值:由电流幅值和内功率角，对电机内的电磁场进行数值计算;通过改变内功率因数角，将计算结果代入电机负载向量关系，以电压、功率、功率因数作为收敛目标进行迭代计算，即可确定电机的不同状态下的单元内磁密。定子铁心分成齿部与轭部，提取每个单元磁密，利用公式1［13］确定定子每个单元的铁耗，求和计算出定子总铁耗。

式中:n为剖分的单元数;p(W)为定子铁耗值;pe(W)为每个单元的铁耗值;Be(T)为定子铁心内单元的磁通密度;q为B=1 T、f=50 Hz时，硅钢片的单位损耗;Ge(kg)为单元硅钢片的重量;ka是铁损增加系数，定子齿部取1.5，定子轭部取1.3。

1.2 等效导热系数的确定

对于绕组内的铜导体与绝缘材料的复杂分布，为简化分析，对定子槽做如下假设:

1)浸渍状况良好，浸渍漆填充均匀;

2)铜线的绝缘漆分布均匀;

3)槽绝缘和铁心紧密结合在一起;

4)槽内各个导线的温差忽略不计。

根据以上假设，可将定子槽内的绕组、绝缘与气体等各种材料效成一个与槽等体积的绕组，其导热系数的计算可根据公式2确定［14－15］。

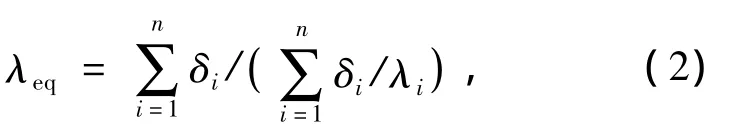
式中:λeq(W/m·K)为槽内材料的等效导热系数;δi(i=1，2，3，…，n)(m)为槽内各种材料的等效厚度;λi(W/m·K)为各种材料的导热系数。

计算定转子全域温度场时，需要对气隙进行特殊处理。转子的旋转带动气隙中空气的流动，使得定子与气隙之间以及转子与气隙之间主要以对流方式换热。为简化计算分析，引入有效导热系数λeff(W/m·K)，它是用静止流体的导热系数来描述气隙中流动空气的热交换能力。这样可以用导热方式换热的效果等价气隙中对流方式换热的效果。

由于气隙中的空气流动为紊流，这种状态下，气隙的有效导热系数可用下式计算［15］，即

1.3 耦合模型中流体的数学描述

由流体传热理论和采用有限体积法建立电机表面通风冷却过程的数学模型，流体流动过程通过以下方程组［11－12］进行描述和控制:

假设流体不可压缩，故流体密度为常值，流体质量守恒方程为

式中:ρ(kg/m3)为流体的密度;u(m/s)为流体的速度矢量;t(s)为时间。

流体动量守恒方程为

式中:F(N)为流体受到的质量力;p(N)为流体压力;μ为流体的粘性系数。

自然界的大气流动以湍流流动为最常见。采用标准k－ε模型能够很好的模拟一般的湍流［12］。标准模型使用湍流动能k和扩散因子ε的通用控制方程，即

式中:φ、V为通用变量;Γ为扩散系数;S为源项。

2 样机的三维温度场耦合计算与实验对比

2.1 实验样机的计算模型

以一台小型离网式永磁同步风力发电机为样机，建立该电机的三维温度场计算模型，描述了电机与大气流动的耦合传热过程。为了简化模型与计算难度，假设机壳表面通风条件一致;电机定子绕组端部等效成与定子槽内绕组等截面积的平行体;电机外围的大气为一层足够大的气层流域，边界为绝热面。其三维温度场的计算模型如图1所示，其中，面S1是自然风入风侧，面S2是出风侧，面S3即机壳外表面是电机的散热面。

实验电机主要参数为:额定容量400 W;额定风速8 m/s;定子外径0.15 m;转子外径0.0922 m;轴向长度0.06 m;永磁体厚度4.5 mm;定子槽数33;三相，极数10。

流体模型在求解温度中，除要满足方程(4)～(6)外，还须满足如下能量守恒方程

式中:U为流体的速度矢量;u、v、w为流体的速度分量;h为流体的比焓;T为流体温度;λ为流体的导热系数;Sh为流体的内热源;Φ为由于粘性作用机械能转化为热能的部分，称为耗散函数。

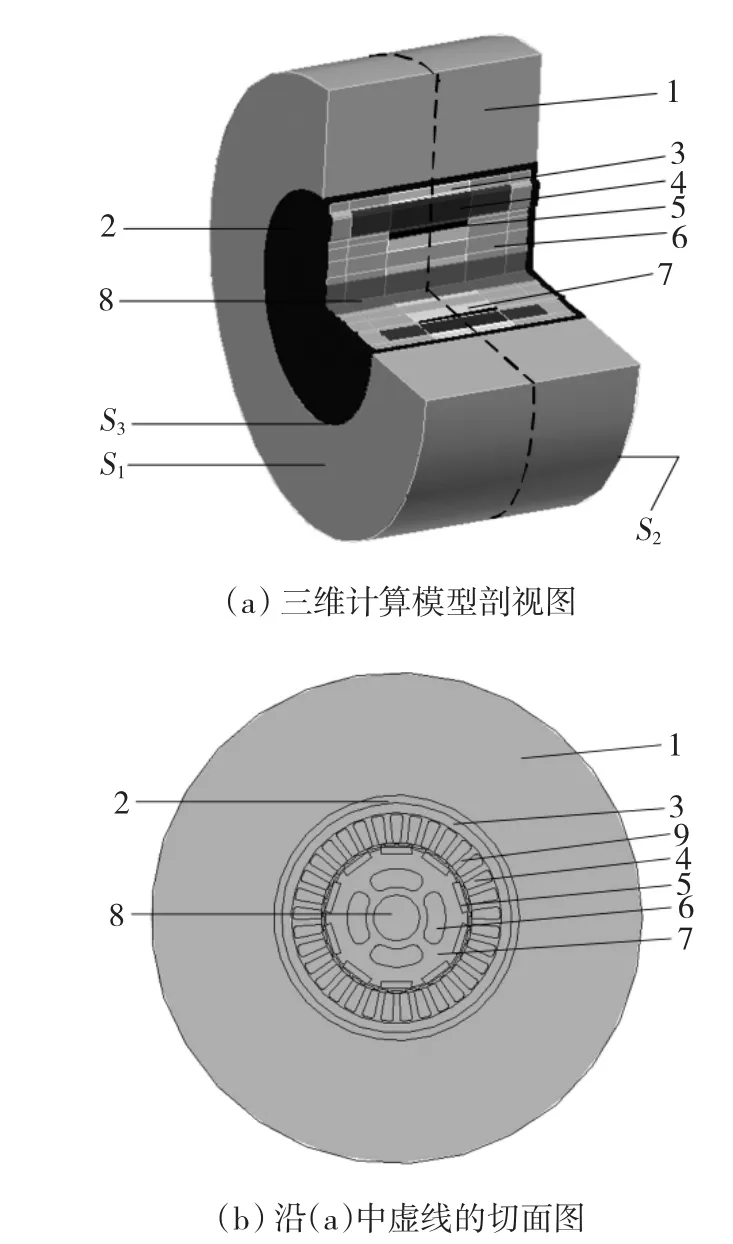
图1 实验电机三维温度场的计算模型Fig.1 The 3-D temperature field calculated model of the prototype

根据流动和传热特点，给出模型求解边界条件为:

1)电机自然风冷却，面S1定义为风速入口边界条件，根据外界条件设定入口风速的大小与温度;面S2定义为出流边界条件。

2)模型中的定子齿部、定子轭部以及定子绕组均给定为热源体。

在热源、固体的导热系数、边界条件和流体状态已知条件下，由流体传热理论来求解电机内的温度场。

2.2 计算结果与实验值对比

为了印证计算方法的可行性，本文利用电机的实验数据与计算的结果做对比验证。实验中机壳表面的风速由EY3－2A电子微风仪测定;采用热敏电阻测量电机内各部分的温度;用Raytek红外测温仪测量机壳的温度。

本文在不同负载情况和不同的风速情况下，进行温升实验，表1显示其中3种工况下实验数据［16］。根据测量结果，进行铜耗和定子各部位铁耗的计算。将各种损耗转换成热流密度施加于电机温度场模型中，依照上述的计算方法，进而可计算电机内温度分布。

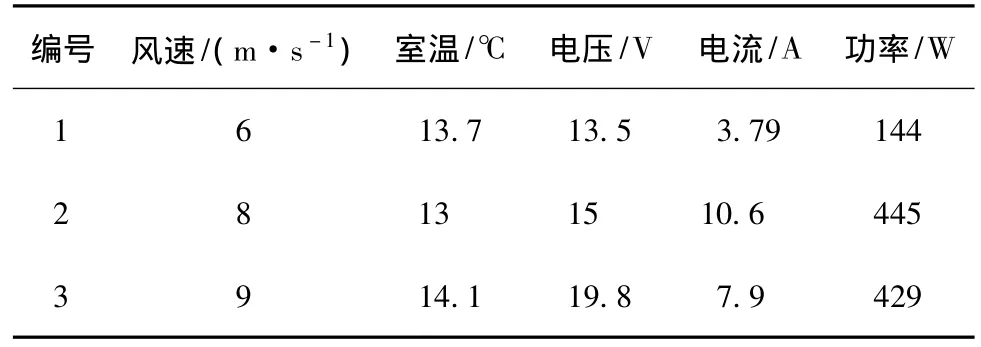
表1 3种不同工况实验数据Table 1 Test data at three different states

图2是第3种工况下，电机三维温度场沿中轴线的横切图与纵切图。表2是电机3个部位温度的测量值与计算值对照。

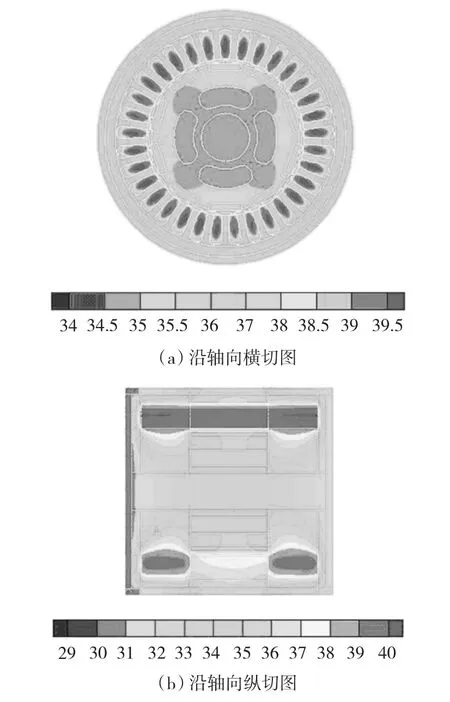
图2 样机温度场计算结果Fig.2 The calculated result of the prototype

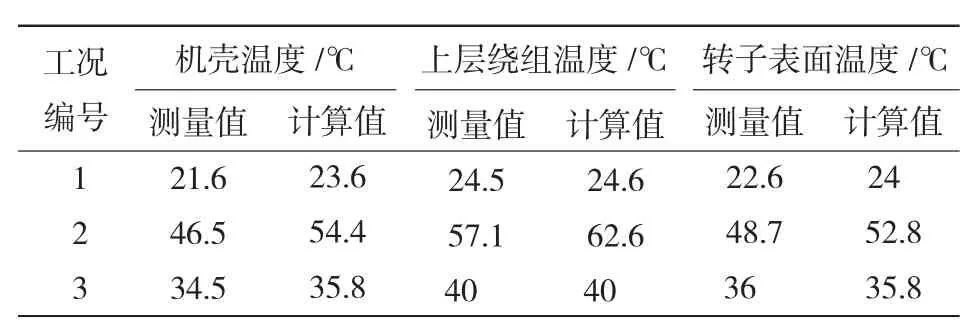
表2 计算值与实验值对比Table 2 Comparison in the calculated and measured results

3 1.5 MW永磁半直驱风力发电机三维温度场计算与分析

3.1 建立耦合计算模型

由表2可以看出，计算结果与实测值比较接近，说明计算方法可行。根据相同计算方法，本文对一台采取表面自然风冷却的1.5 MW永磁半直驱风力发电机进行三维温度场计算与分析。该风力发电机的主要参数为:额定容量1500 kW;额定转速150 r/min;额定电压690 V;定子外径2.2 m;额定风速15 m/s;轴向长度0.62 m;气隙长度7 mm;定子槽型11.5 mm×64 mm;永磁体厚度64 mm。

根据电机对称关系理论，取电机的一个单元进行三维温度场计算，其计算模型如图3所示，其中，面S1是自然风入风侧，面S2是出风侧，面S3即机壳外表面是电机的散热面。

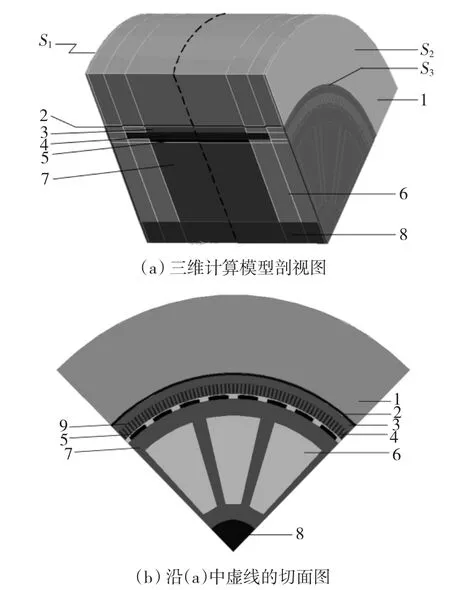
图3 1.5 MW PMSG三维温度场的计算模型Fig.3 The 3-D temperature field calculated model of the 1.5 MW PMSG

3.2 计算结果与分析

在额定风速下，风力发电机功率达到额定值，也即最大值。图4是在环境温度为20℃，额定风速15 m/s时，半直驱风力发电机三维温度场沿中轴线的横切面图与纵切面图。

图4 1.5 MW PMSG计算结果Fig.4 The calculated result of the 1.5 MW PMSG

由于定子绕组和定子铁心是电机的主要热源，转子侧损耗小，电机外表面是主要的散热途径，所以最高温度出现在上层定子绕组。考虑到端盖与轴具有一定的散热作用，转子铁心由外向内温度递减。

图5是定子绕组沿轴向的最高温度分布图。由于封闭式风冷的电机，内部无散热风沟，绕组端部散热条件差，温度较绕组中部要高。由于入风侧的散热条件好于出风侧的，所以上风侧的绕组端部温度会略低于下风侧的端部绕组。

图5 绕组轴向温度分布图Fig.5 The axial temperature distribution of windings

兆瓦级风力发电机的工作条件往往在野外或海上，四季温差和昼夜温差都比较大。一般考虑环境温度在－20～40℃，图6是发电机工作在额定状态下，不同环境温度时，电机额定状态下各部的温度变化图。

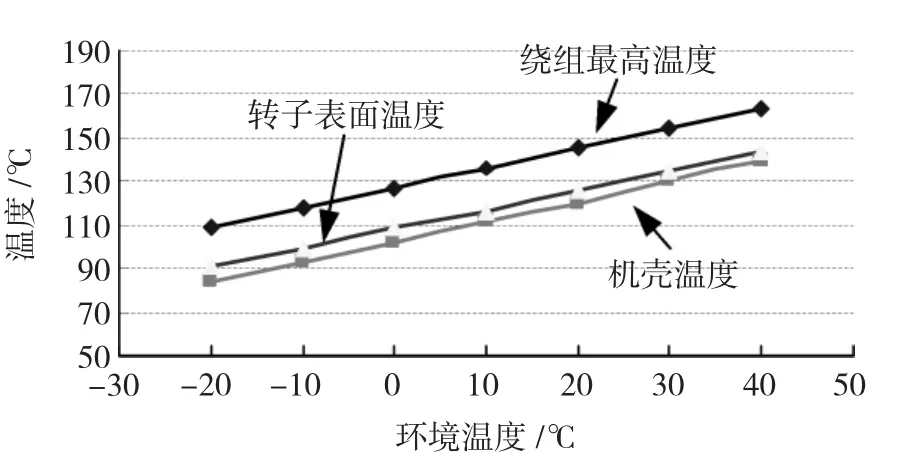
图6 不同环境温度下电机的温度Fig.6 The temperature of generator at different ambient temperature

风机的切入风速为3 m/s，切出风速为25 m/s，在低于额定转速时，假定风机运行在浆距角为0、最佳叶尖速比的状态下;高于额定风速时，变浆距机构发挥作用，使电机转速限制在额定值附近。故给定其渐变风风速与电机转速的关系［17］如图7所示。在额定转速以下，电机输出功率由式(8)［18］的比例关系确定。在额定风速以上时，电机以额定功率输出，表3是不同风速下的损耗分布。由此计算在20℃环境温度、不同风速状态下电机各部温度，如图8所示。

式中:Pm为风力机所捕获的能量;Cp为功率利用系数;ρ为空气密度;A为风叶扫过的面积;υ0为风速。

由于风机吸收的功率与风速的三次方成正比，所以在低于额定转速时，电机温度随风速的增大而快速增高;当超过额定转速后，电机恒功率输出，机壳表面风速增加，使其温度随着风速的增加而缓慢降低。

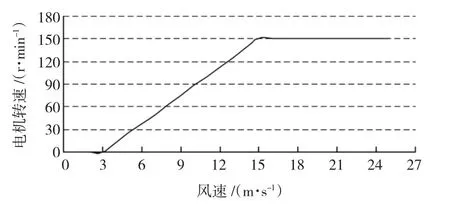
图7 给定风速与电机转速关系Fig.7 The given relation between wind speed and generator rotary speed

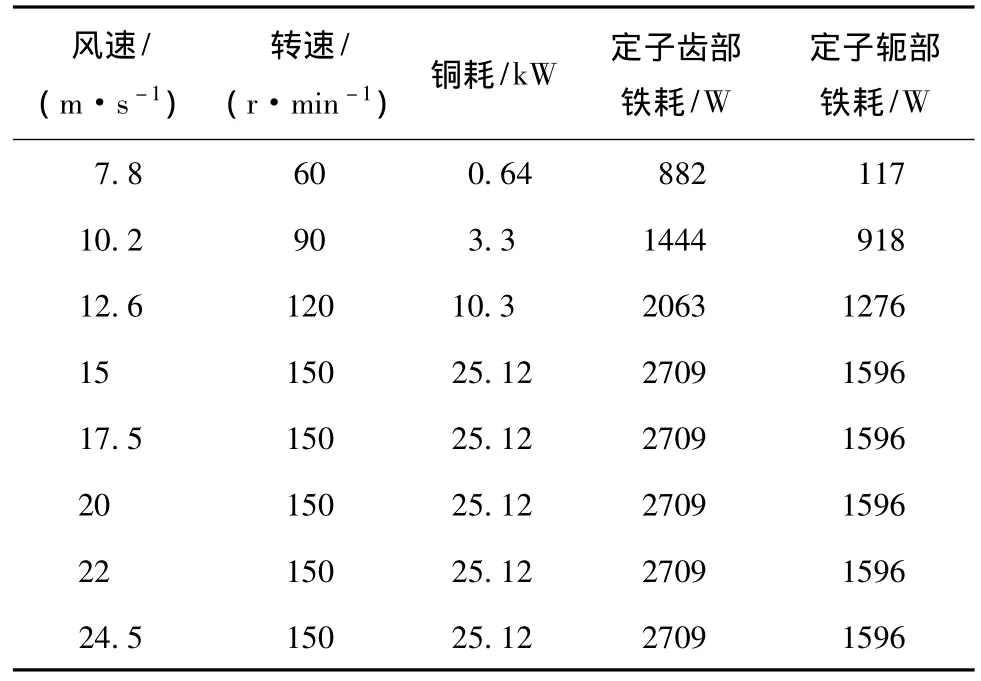
表3 不同风速下电机损耗Table 3 The loss distribution at different wind speed

图8 不同风速下电机温度Fig.8 The temperature of generator at different wind speed

4 结论

通过对实验样机温度场的计算结果与实验值对比，以及对1.5MW半直驱式永磁同步风力发电机的三维温度场计算，可以得出如下结论:

1)通过对小型实验样机三维温度场的计算与实验结果对比，验证了计算的准确性，说明文中所采取热源、等效散热系数的计算方法以及流体传热计算模型的可行性。为表面自然风冷却电机的温度场计算提供了参考。

2)通过三维温度场的计算可以得出自然风冷却电机沿轴、径向温度的分布规律。在径向上最高温度出现在定子绕组上层。在轴向上，由于端部散热能力较差，导致绕组端部温度要高于绕组中部，并且电机入风侧的温度要低略于出风侧的。

3)对于变速恒频的大型永磁同步风力发电机，在额定风速附近电机温度达到最高。低于额定风速时，电机温升随风速的增加而快速增大;高于额定风速后，电机温升随风速的增加而缓慢降低。

［1］张岳，王凤翔.直驱式永磁同步风力发电机性能研究［J］.电机与控制学报，2009，13(1):78 －82.ZHANG Yue，WANG Fengxiang.Performance research on permanent magnet synchronous generator directly driven by wind turbine［J］.Electric Machines and Control，2009，13(1):78 －82.

［2］姚若萍，饶方权.蒸发冷却水轮发电机定子温度场研究［J］.中国电机工程学报，2003，23(6):87 －90.YAO Ruoping，RAO Fangquan.Analysis of 3D thermal field in the stator of large hydro-generator with evaporation-cooling system［J］.Proceedings of the CSEE，2003，23(6):87 －90.

［3］温志伟，顾国彪.实心磁极同步电动机转子温度场计算［J］.大电机技术，2005(2):1 －5.WEN Zhiwei，GU Guobiao.Calculation of rotor temperature field for solid pole synchronous motor［J］.Large Electric Machine and Hydraulic Turbine，2005(2):1 －5.

［4］黄学良，胡敏强，周鹗.电机三维温度场新的有限元模型［J］.中国电机工程学报，1998，18(2):78 －82.HUANG Xueliang，HU Minqiang，ZHOU E.Novel FEM method to compute 3D thermal distribution of electrical machine［J］.Proceedings of the CSEE，1998，18(2):78 －82.

［5］BOGLIETTI A，CAVAGNINO A，LAZZARI M，et al.A simplified thermal model for variable-speed self-cooled induction motor［J］.IEEE Transactions on Industry Applications，2003，39(4):945－952.

［6］魏永田，孟大伟.电机内热交换［M］.北京:机械工业出版社，1998:251－344.

［7］GUO Jianzhong，GUO Hui，HOU Zhe.Rotor temperature monitoring technology of direct-drive permanent magnet wind turbine［C］//2009 International Conference on Electrical Machines and Systems，November 15 －18，2009，Tokyo，Japan.2009:1 －4.

［8］路义萍，马贤好，李伟力.空冷汽轮发电机转子风道结构对传热的影响［J］.中国电机工程学报，2007，27(17):61 －66.LU Yiping，MA Xianhao，LI Weili.The effect of geometry factors on heat transfer of rotor’s cooling duct of large turbo generator with air-coolant［J］.Proceedings of the CSEE，2007，7(17):61 －66.

［9］霍菲阳，李勇，李伟力，等.大型空冷汽轮发电机定子通风结构优化方案的计算与分析［J］.中国电机工程学报，2010，30(6):69－75.HUO Feiyang，LI Yong，LI Weili，et al.Calculation and analysis on stator ventilation structure of different optimum proposal in aircooled turbogenerator［J］.Proceedings of the CSEE，2010，30(6):69－75.

［10］孟大伟，刘宇蕾，张庆军，等.潜油电机整体三维温度场耦合计算与分析［J］.电机与控制学报，2010，14(1):52 －55.MENG Dawei，LIU Yulei，ZHANG Qingjun，et al.Calculation and analysis of 3D temperature of the submersible motor based on coupled field［J］.Electric Machines and Control，2010，14(1):52 －55.

［11］张梓雄，董曾南.粘性流体力学［M］.北京:清华大学出版社，1998:58－101.

［12］吴德铭，郜冶.实用计算流体力学基础［M］.哈尔滨:哈尔滨工程大学出版社，2006:117－266.

［13］汪耕，李希明.大型汽轮发电机设计、制造与运行［M］.上海:上海科学技术出版社，2000:148－151.

［14］XYPTERAS J，HATZIATHANASSIOU V.Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect［J］.IEEE Transactions on Energy Conversion，1999，14(4):996 －1003.

［15］HATZIATHANASSIOU V，XYPTERAS J，ARCHONTOULAKIS G.Electrical-thermal coupled calculation of an asynchronous machine［J］.Archiv Fur Electrotechnik，1994，77(2):117 －122.

［16］李伟力，仝世伟，程鹏.离网型永磁同步风力发电机电磁场和温度场数值计算与分析［J］.中国电机工程学报，2010，30(30):107－113.LI Weili，TONG Shiwei，CHENG Peng.Calculation and analysis of electromagnetic and temperature fields in off-grid type permanent magnet synchronous generator［J］.Proceedings of the CSEE，2010，30(30):107 －113.

［17］陈昆明，汤天浩，陈新红，等.永磁半直驱风力机控制策略仿真［J］.上海海事大学学报，2008，29(4):39 －44.CHEN Kunming，TANG Tianhao，CHEN Xinhong，et al.Control strategy simulation on half-direct permanent magnet wind energy conversion system［J］.Journal of Shanghai Maritime university，2008，29(4):39 －44.

［18］王承煦，张源.风力发电［M］.北京:中国电力出版社，2003:56－57.