木材干燥微波－真空木材干燥过程ARMA模型建立及其控制器仿真

孙丽萍， 曹军， 李志辉

(东北林业大学机电工程学院，黑龙江 哈尔滨 150040)

0 引言

微波-真空干燥是一项新的综合干燥方法，采用先进的测控手段，设计高精度、低成本、实时性强、稳定可靠的微波-真空木材干燥自动测试系统将推动木材干燥自动控制系统的发展［1-5］。文中针对花旗松的微波-真空干燥工艺，建立时间序列下的自回归滑动平均(auto-regressive and moving average，ARMA)数学模型，设计了一种fuzzy-PID自整定控制器，应用Matlab/SIMULINK工具对干燥窑常规PID控制和fuzzy-PID自整定控制进行仿真，fuzzy-PID自整定控制器的阶跃响应曲线具有上升快，稳态性能好，过渡过程时间短，超调量小等特点，能够提高木材干燥过程的控制水平。

1 试验方法

试验的材料为花旗松锯材，试验中微波加热采用了间歇辐射方式，微波辐射一段时间，再停止辐射一段时间，如此反复直至整个干燥过程结束。在干燥初期开启7 min，关闭3 min;干燥后期开启8 min，关闭2 min。为了保证干燥质量，试材的中心最高温度不能超过85℃。如图1所示，木材的中心温度能够维持在设定的55～65℃之间。

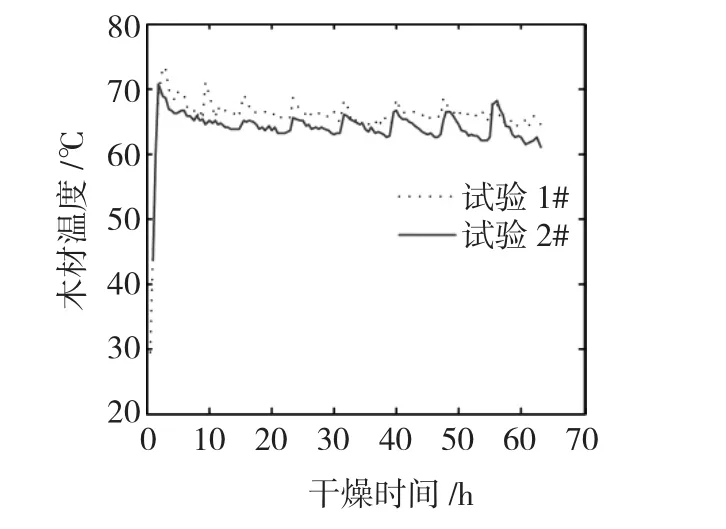
图1 干燥过程的温度曲线Fig.1 Temperature curve of wood drying process

图2 干燥过程的含水率曲线Fig.2 LMC curve of wood drying process

图2给出对应试材干燥过程的含水率(Lumber moisture content，LMC)变化曲线，试材的含水率下降速度基本相同，且呈等速下降趋势。由于在不同温度、压力、相对湿度条件下试材的含水率与时间的关系又有不同，需要进行大量的试验，并建立数据库，得到更合理的干燥工艺过程。

2 ARMA模型原理

ARMA模型是研究时间序列的重要方法，由自回归模型与滑动平均模型为基础“混合”构成。一般的系统方程写成ARMA模型的形式［6-8］为

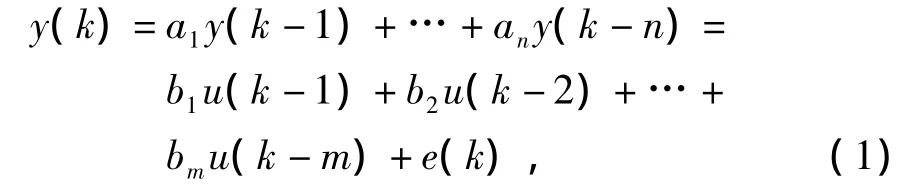
式中:u为系统输入;y为系统输出;e为测量噪声。其中n≥m，n为任意值。等式(1)可以以z域的形式写成

对于二阶ARMA模型，系统等式为

式中y(k)代表平均温度读数，平均含水率读数或者平均相对湿度读数;当输入u(k)代表加热器输入时，而且代表第一个子系统加热器输入或者第二个子系统的平均温度输入;e(k)是估计误差。令e(k)=0，等式(3)写成z域的形式为

式中相关的z域的转换方程为

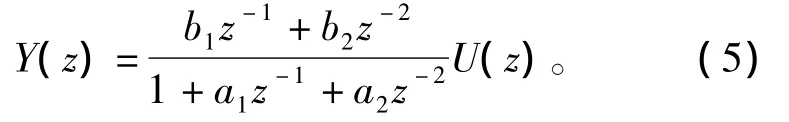
利用输入输出测量值进行系统(模型)辨识，向干燥窑内施加白噪声输入信号(一种形式的脉冲调宽信号)可以激活所有的系统动态模型。使用收集到的输入输出(I/O)数据，其中包含控制系统的动态信息，建立适合干燥窑系统不同过程的输入输出模型。估算出相关模型参数，在最小方差的意义上表示出最适合的数据。

鉴于干燥窑的复杂性，相比解析模型也就是模型辨识，要更多地进行动态实验模型的研究。

3 参数估计

在单输入单输出模型下，估计温度、含水率的模型参数。微波加热器的开/关控制信号由计算机给出，参数估计值符合加热器输入信号和每个输出变量大小之间的关系。参数估计过程中要选择能合理表示干燥过程的系统阶次。

将干燥窑模型分为两个子模型，分别称为加热-温度模型和温度-含水率模型，如图3所示。每个子模型都是单输入单输出(single-input-single-output，SISO)模型，加热-温度(第一个)子系统输入为微波加热控制的开关信号，温度传感器读数为输出信号;温度-含水率(第二个)子系统输入为温度传感器读数，干燥窑内相关传感器的含水率读数为输出信号。

图3中uh为微波加热器的控制信号(ON/OFF);yt为温度响应(加热-温度模型的输出);ym为含水率响应(温度-含水率模型的输出)。通过在Matlab中执行算法，根据干燥窑实时输入输出数据辨识系统模型的参数。

图3 模型识别框图Fig.3 Block diagram of model identification

3.1 SISO加热－温度模型

针对试验数据，给出试验1#温度响应的模型辨识结果，模型结构为二阶SISO系统，参数估计值如图4所示，迭代次数均为200次。下述模型分析所列结果图均采用同一组数据。

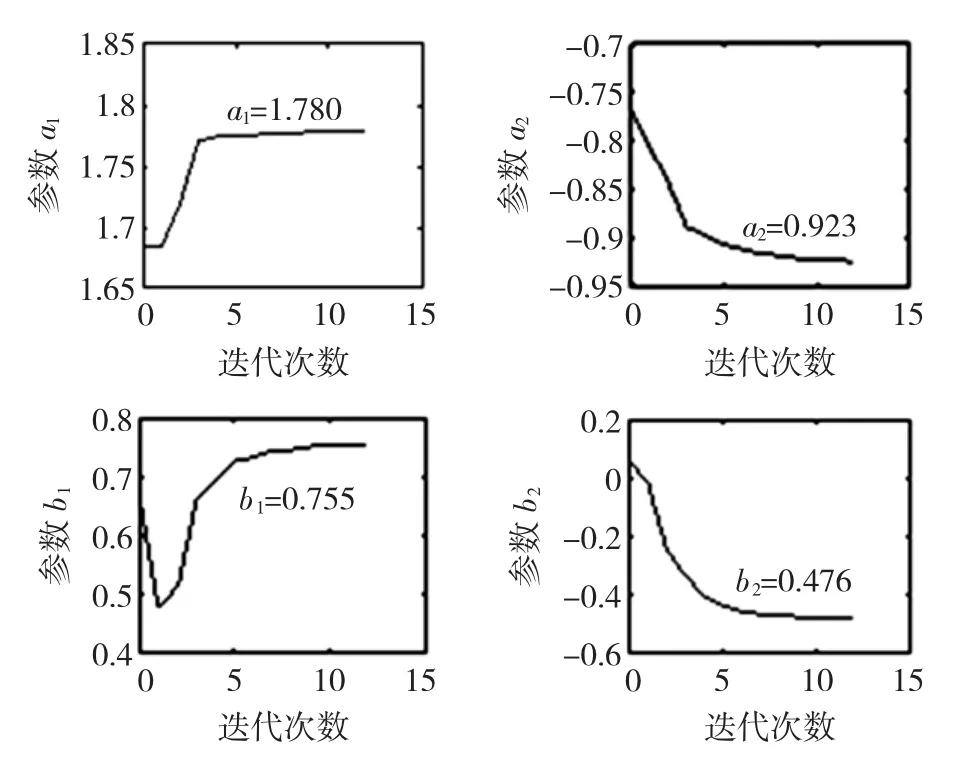
图4 二阶加热－温度模型的参数估计Fig.4 Parameter estimation for the 2nd order heat-temperature model

二阶SISO温度模型参数估计结果总结在表1中。估计结果表明参数a1和a2一致性较好，然而参数b1和b2则一致性较差，原因在于解析模型是基于不同试材，给定不同的温度、压力、相对湿度等初始条件，根据输入输出数据建立的，因此，模型参数在一定范围内摄动。

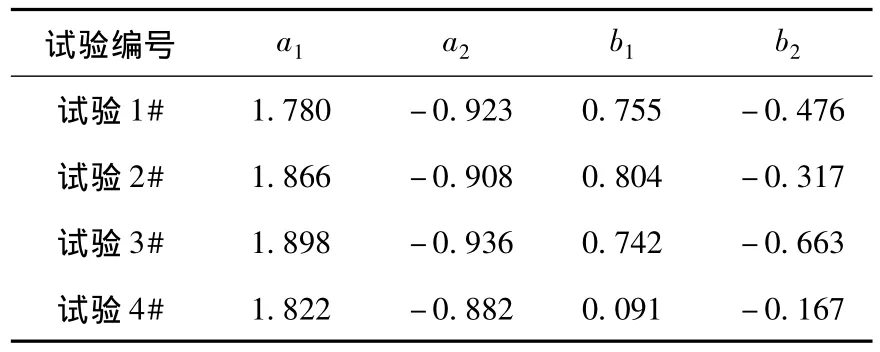
表1 二阶SISO加热－温度模型估计的参数值Table 1 Parameter value for 2nd order SISO heat-temperature model

3.2 SISO温度－含水率模型

上面建立了SISO系统的二阶温度-含水率模型，试材的含水率初始值为40%左右，迭代次数仍为200次。二阶温度-含水率模型的参数估计值如图5所示。

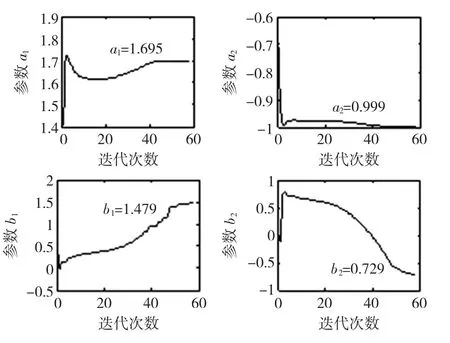
图5 二阶温度－含水率模型的参数估计Fig.5 Parameter estimation for the 2nd order temperature-moisture model

二阶SISO温度-含水率模型参数估计结果列入表2中。不论参数a1和a2还是参数b1和b2均表现出较好的一致性。结合对含水率实验数据的分析得知，在不同初始含水率条件下的试材，表现出等速干燥特点，外界因素对其影响较小。

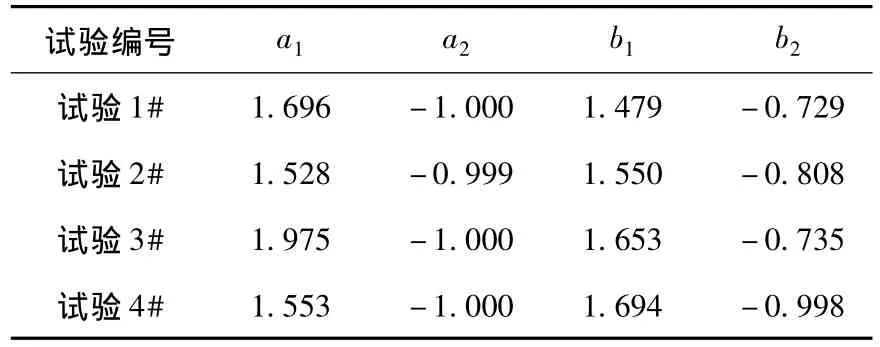
表2 二阶SISO温度－含水率模型估计的参数值Table 2 Parameter value for 2nd order SISO temperature-moisture model

4 模型确立

通过输入输出数据得到参数估计值，建立温度响应与含水率响应下的SISO状态空间二阶模型。模型参数估计时，微波加热器的控制信号为输入值，同样，将其应用到状态空间模型中，与实际干燥窑的实验响应比较，判断模型响应的准确性。模型的准确性使用方差描述，在许多实际问题中，研究随机变量和均值之间的偏离程度其。主要步骤是:1)使用相同的输入输出数据集合计算二阶模型参数;2)通过每两个模型的实际数据与模型响应得到方差值;3)通过式(6)和标准差计算均方差。

在有限测量次数中，均方根误差(root mean square error，RMSE)常表示为

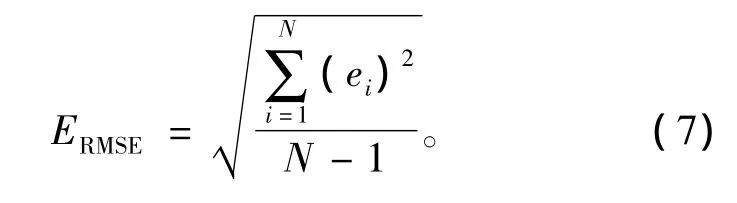
式中:ei为一组测量值与平均值的偏差，i=1，2，3，…，N;N为测量次数。

4.1 SISO加热－温度模型的确立

根据参数估计阶段加热-温度模型中4组试验，给出了干燥窑的实际响应曲线，并运用相同的输入输出数据集合得到的二阶模型响应曲线，同时可以求得模型的方差，绘制出的曲线如图6所示。

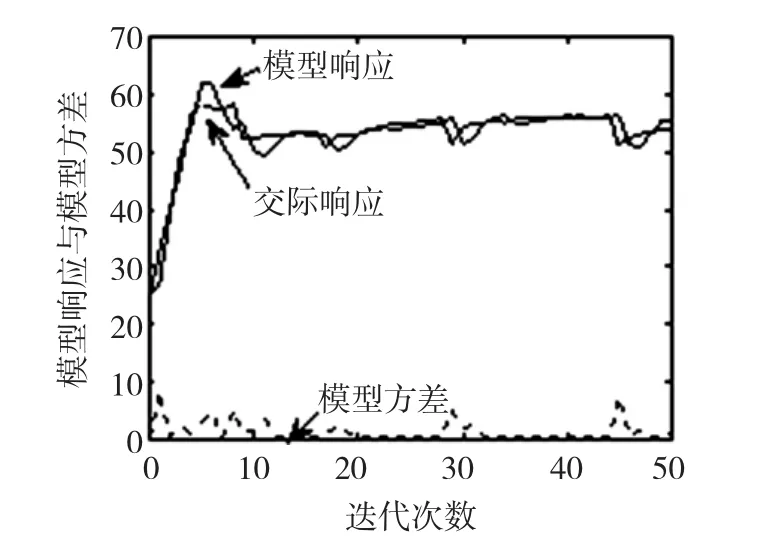
图6 二阶加热－温度模型的确立Fig.6 Validation of the 2nd order SISO heat-temperature model

每个试验中的RMSE和标准偏差(standard deviation，STD)如表3所示，可以看出每组试验的模型响应与实际响应之间的ERMSE和标准偏差S的误差都比较大。但是使用二阶SISO结构的加热-温度模型响应与干燥窑的实际响应曲线趋势相同，在模型响应初期都不同程度的高于实际响应。

表3 加热－温度模型的误差值Table 3 Error value for heat-temperature model

4.2 SISO温度－含水率模型的确立

根据试验数据确立二阶温度-含水率模型曲线和实际响应曲线，并给出模型响应与干燥窑的实际试验响应之间的方差，如图7所示。图中可以看出二阶温度-含水率模型响应比较接近实际响应，得到比较高的拟合度，干燥过程的含水率变化具有一定的线性特征。

图7 二阶温度－含水率模型的确立Fig.7 Validation of the 2nd order SISO temperature-moisture model

每个试验中的RMSE和标准偏差如表4所示，尽管模型的响应比较理想，但是个别试验的模型响应与实际响应之间的ERMSE和S的误差仍比较大，在现场控制的模型选择上不能满足每组试材的工艺要求，需要在最接近模型的基础上采用智能手段进行实时调整。

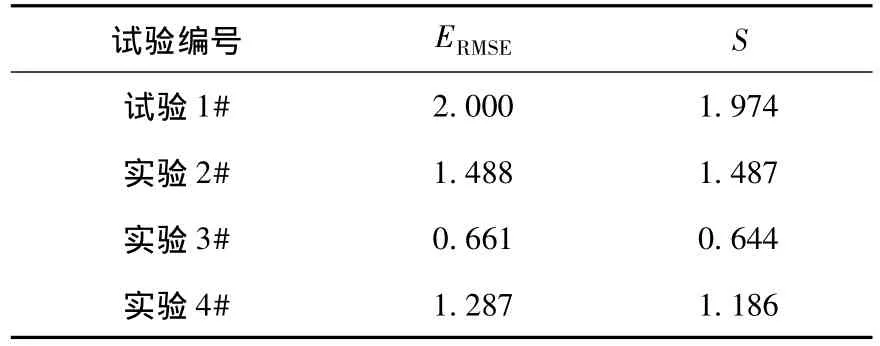
表4 温度－含水率模型的误差值Table 4 Error value for temperature-moisture model

5 模型指数

模型指数(model index，MI)称干燥窑时间响应与估计模型响应之间的RMSE的比值，用p表示。假定控制输入序列{u(1)，u(2)，…，u(N-1)，u(N)}，并将其应用到系统中，相应地系统实际响应序列为{y(1)，y(2)，…，y(N-1)，y(N)}，模型输出序列为{^y(1)，^y(2)，…，^y(N-1)，^y(N)}，估计误差值序列为{e(1)，e(2)，…，e(N-1)，e(N)}，平方差［9-12］表示为

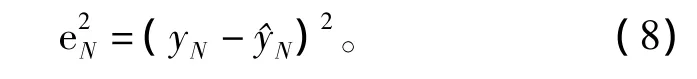
则均方差为

给出估计误差的均方根ERMSE为

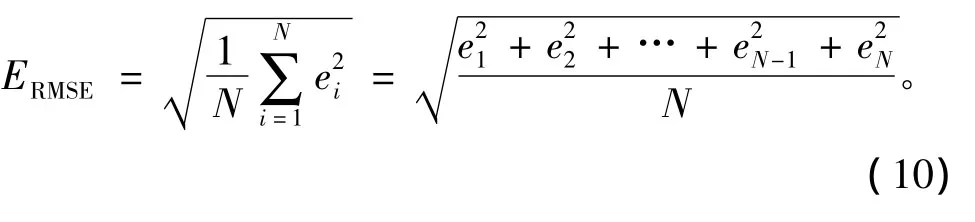
同样，实际响应的均方根ERMS0为

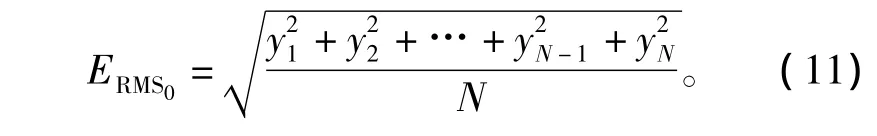
模型指数定义为

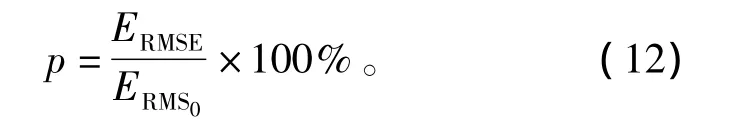
可以明显地看到模型指数是模型是否能表示实际系统的指标，它是一个百分比的形式。MI的值越大，表明实际响应与模型响应的估计误差越大。在上一节模型确立中对应的4个试验的模型指数如表5所示。

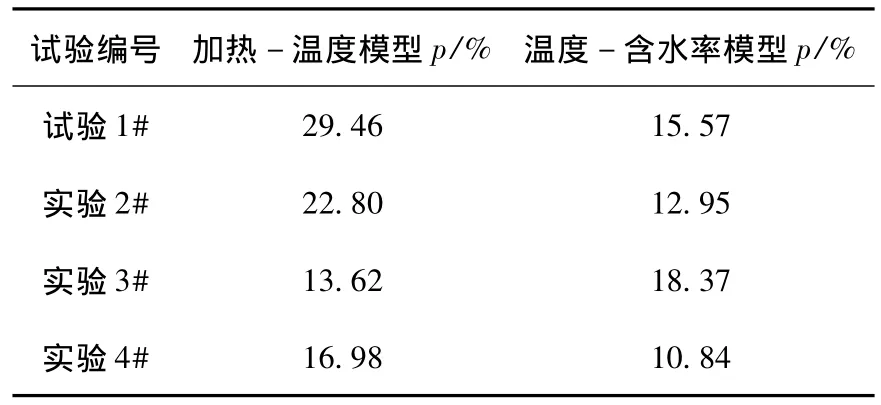
表5 模型指数Table 5 model index values

对比模型指数可以发现，其中温度-含水率模型的稳定性相对加热-温度模型较好，p在10% ～20%之间。而木材中心温度以及含水率的p变化受不同试材的微结构、初含水率等因素的影响较大，从而进一步说明木材干燥过程表现出很强的非线性。

常规控制手段中仍然需要有具体的模型结构，试验4#中温度-含水率模型最佳，然而对应的加热-温度模型较差，同时结合模型确立的分析结果，选用二阶平均模型作为常规PID控制的系统模型，根据模型估计的参数值及模型指数，最终模型参数如表6所示。

表6 两个子模型的ARMA参数Table 6 ARMA parameter values for two sub-models

因此加热-温度过程与温度-含水率过程二阶ARMA模型的仿真结果分别表示为

6 Fuzzy-PID自整定控制器设计与仿真

针对微波-真空干燥花旗松得到试验结果，通过Matlab/SIMULINK仿真工具，分别搭建PID仿真图和fuzzy-PID自整定仿真图，图8为fuzzy-PID自整定仿真图主程序。

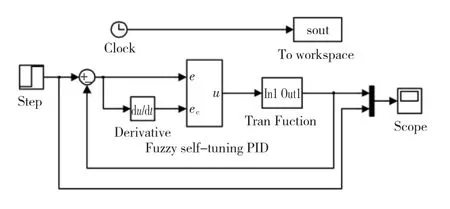
图8 木材干燥fuzzy－PID自整定仿真图主程序Fig.8 Simulation diagram of main programfor fuzzy self-tuning PID of wood drying

仿真研究中，为了验证控制器的效果，对某一阶段的干燥参数设定选用阶跃响应信号，如给定温度输入60℃，温度初始值45℃，含水率输入16%，含水率初始值18%。仿真时间设为100 min，采样时间为30 s，模型仿真结果分别如图9、图10所示。

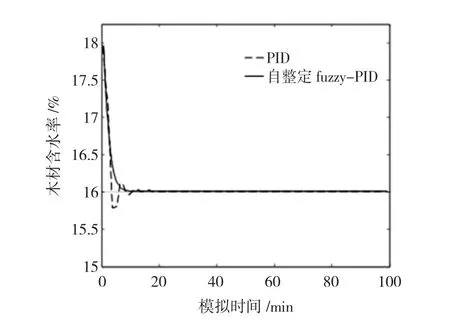
图9 木材干燥含水率仿真图Fig.9 Simulation diagram of LMC of wood drying

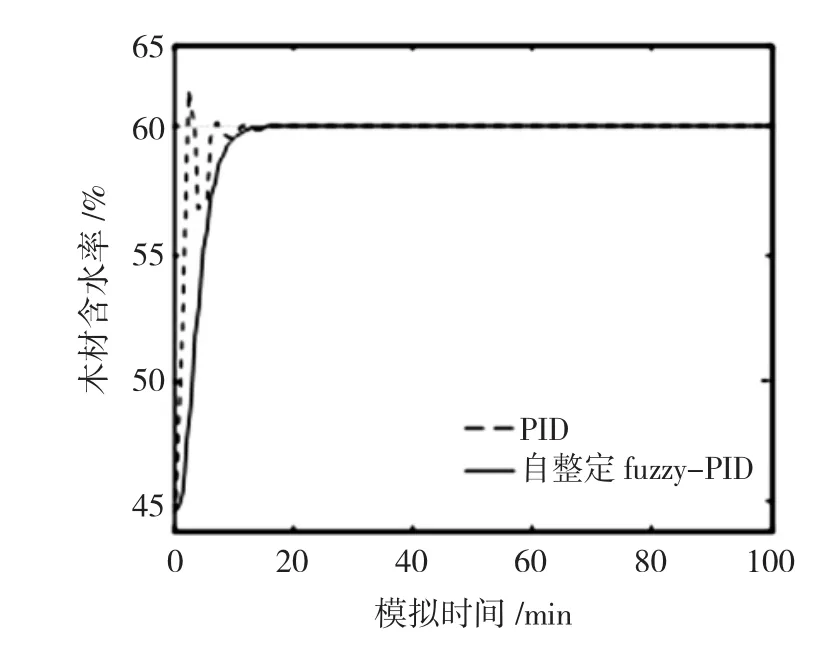
图10 木材干燥温度仿真图Fig.10 Simulation diagram of temperature of wood drying

仿真结果表明，fuzzy-PID自整定控制系统相对传统PID控制系统得到较好的结果，由于模糊控制器具有灵活性，通过对特定工艺过程使用专家知识，在复杂的系统中也能得到较好的效果。

木材干燥控制系统通常采用PID控制，传统的PID控制是依赖操作人员按照工艺参数凭经验的控制方法，缺乏充分的灵活性，存在着参数修改不方便、不能进行自整定等缺点。模糊自整定PID参数控制系统能在控制过程中对不确定的条件、参数、延迟和干扰等因素进行检测分析，采用模糊推理的方法实现PID参数KP、KI和KD的在线自整定，不仅保持了常规PID控制系统原理简单、使用方便、鲁棒性较强等优点，而且具有更大的灵活性、适应性、控制精度更佳。

7 结语

实现自动控制是木材干燥过程中的重要环节之一，微波真空干燥因其独特的优势拥有广泛的应用前景和使用价值。针对花旗松的微波-真空干燥工艺在时间序列下建立了ARMA数学模型，并对传统PID和fuzzy-PID自整定控制系统分别进行了动态仿真。通过比较分析可得出:传统PID控制有较大的超调量，动态调整时间长，但没有稳态误差;fuzzy-PID自整定控制器的阶跃响应曲线上升快，调节精度高，稳态性能好，过渡过程时间短。对花旗松微波-真空的干燥控制器模型的复杂性，只根据时间与温度及含水率的的曲线，近似得到其数学模型，在实际应用时还应考虑其他因素，例如微波加热功率、真空度等。

［1］过军，朱善国.微波真空干燥设备控制系统的数字化设计［J］.自动化仪表，2008，29(3):47-49.GUO Jun，ZHU Shanguo.Digitization design of control system for microwave vacuum drying equipment［J］.Process Automation Instrumentation，2008，29(3):47-49.

［2］林季孜.木材真空微波加热干燥技术研究［D］.台北:国立台北科技大学冷冻与低温科技研究所，2004:1-4.

［3］LEIKER M，ADAMSKA M A.Energy efficiency and drying rates during vacuum microwave drying of wood［J］.Holz Als Roh-und Werkstoff，2004，62(3):203-208.

［4］CUI Zhengwei，XU Shiying，SUN Dawen.Microwave-vacuum drying kinetics of carrot slices［J］.Journal of Food Engineering，2004，65(2):157-164.

［5］Püschner.Microwave Vacuum Drying for advanced Process Technology［R］.Schüttgut:P?schner，2002.

［6］肖化昆，狄争，钟江帆.一种基于ARMA的仿真控制系统设计［J］.微计算机信息，2006，22(16):119-121.XIAO Huakun，DI Zheng，ZHONG Jiangfan.A process simulation control system design based on ARMA［J］.Control and Automation，2006，22(16):119-121.

［7］PERE C，RODIER E.Microwave vacuum drying of porous media:experimental study and qualitative considerations of internal transfers［J］.Chemical Engineering and Processing，2002，41(5):427-436.

［8］SEYFARTH R，LEIKER M，MOLLEKOPF N.Continuous drying of lumber in a microwave vacuum kiln［C］//8th International IUFRO Wood Drying Conference，August 24-29，2003，Brasov，Romania.2003:159-153.

［9］LAURENT S，COUTURE F，ROQUES M.Vacuum drying of a multicomponent pharmaceutical product having different pseudopolymorphic forms［J］.Chemical Engineering and Processing，1999，38(2):157-165.

［10］CUI Zhengwei，SUN Lijuan，CHEN Wei，et al.Preparation of dry honey by microwave-vacuum drying［J］.Journal of Food Engineering，2008，84(4):582-590.

［11］LEIKER M，ADAMSKA M A，GÜTTEL R，et al.Vacuum microwave drying of beech:property profiles and energy efficiency［C］//Proceedings of the COST Action E155th International Conference on Wood Drying，April 22-24，2004，Athens，Greece.2004:128-137.

［12］蔡自兴，约翰·德尔金，龚涛.高级专家系统:原理、设计及应用［M］.北京:科学出版社，2005:57-72.