Linex损失下二项分布参数的 Bayes估计

谭 玲

（中国矿业大学 理学院，江苏 徐州 221116）

Linex损失下二项分布参数的 Bayes估计

谭 玲

（中国矿业大学 理学院，江苏 徐州 221116）

在 Linex损失函数下讨论了二项分布参数的 Bayes估计，当先验分布取 Beta分布和幂分布时分别给出了参数的 Bayes估计，多层Bayes估计，E－Bayes估计的精确形式，并证明了 Bayes估计的可容许性。

Bayes估计；多层 Bayes估计；E－Bayes估计；可容许性

0 引言

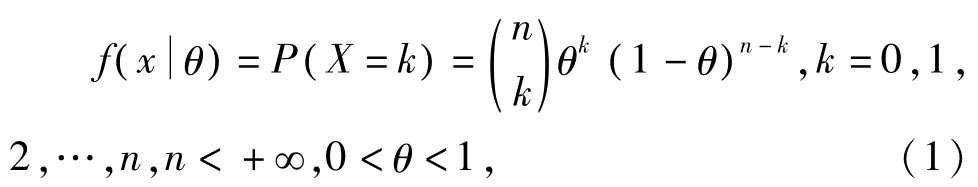
则称随机变量 X服从参数为 θ的二项分布。

自从 Linex损失函数被提出以来，许多学者对其进行了大量的研究，文献［1］研究了 Linex损失下Pareto分布族参数的经验 Bayes估计，文献［2］在Linex损失函数下研究逆高斯分布参数倒数的 Bayes估计，文献［3］研究了 Linex损失下 Rayleigh分布参数倒数的 Bayes估计，文献［4］研究了在Linex损失下指数分布刻度参数 EB估计的渐近最优性，本文在 Linex损失函数下研究二项分布参数的 Bayes估计。

定义［5］若随机变量 X的分布密度为

1 参数 θ的 Bayes估计

设 X服从二项分布，X1，X2，…，Xn是来自总体为 X的容量为 n的简单随机样本，x1，x2，…，xn为X1，X2，…，Xn的实现值，由（1）得X1，X2，…，Xn的联合密度函数为

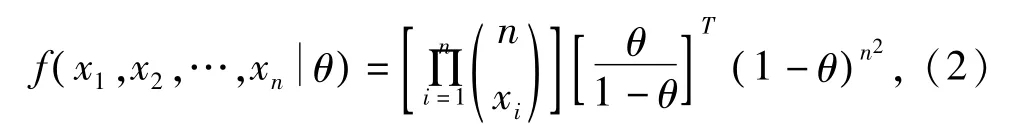
取 Linex损失函数为

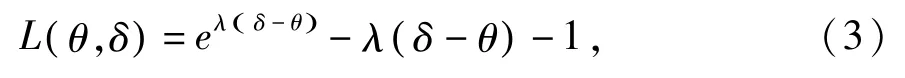
其中 λ为不等于零的常数，δ为 θ的估计。

下面讨论参数θ的Bayes估计，设θ先验分布G (θ)，且G(θ)有密度dG(θ)＝g(θ)dθ。

引理1［6］在Linex损失函数（3）下，对于 θ的任一先验分布 g(θ)，θ的Bayes估计为

定理1 在Linex损失函数（3）下，取 θ的先验分布为 Beta分布，记为βa，( )b，则二项分布参数θ的 Bayes估计为

证明：由于参数θ的先验分布为 Beta分布，所以 θ的先验概率密度函数为

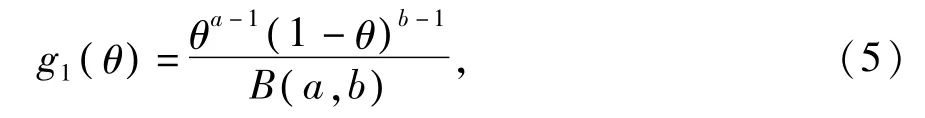
其中参数 a＞0，b＞0，

可得 θ的后验概率密度为

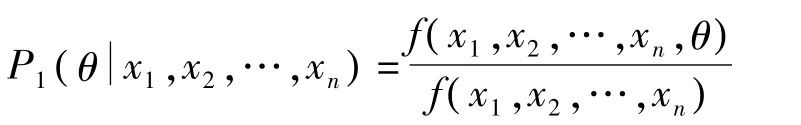
所以后验分布服从 Beta分布

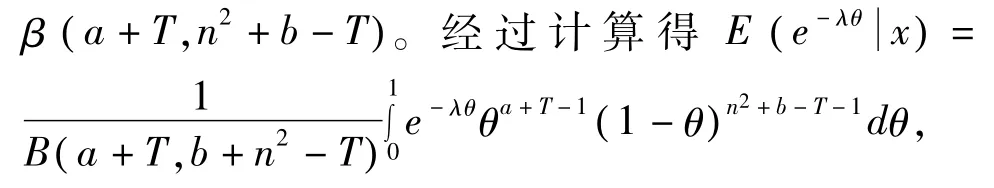
定理2 在 Linex损失函数（3）下，取 θ的先验分布为幂分布，则二项分布参数 θ的 Bayes估计为

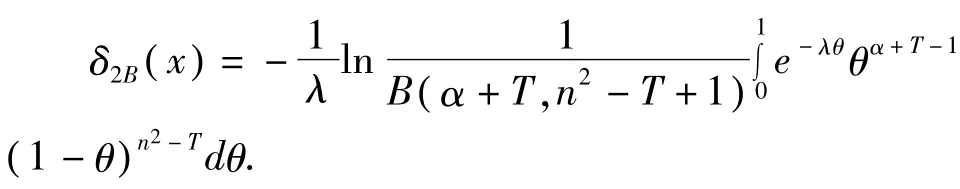
证明：因为参数 θ的先验分布为幂分布，所以 θ的先验概率密度函数为

其中0＜θ＜1，α＞0为超参数，

由（2），（7）可得 θ的后验概率密度为

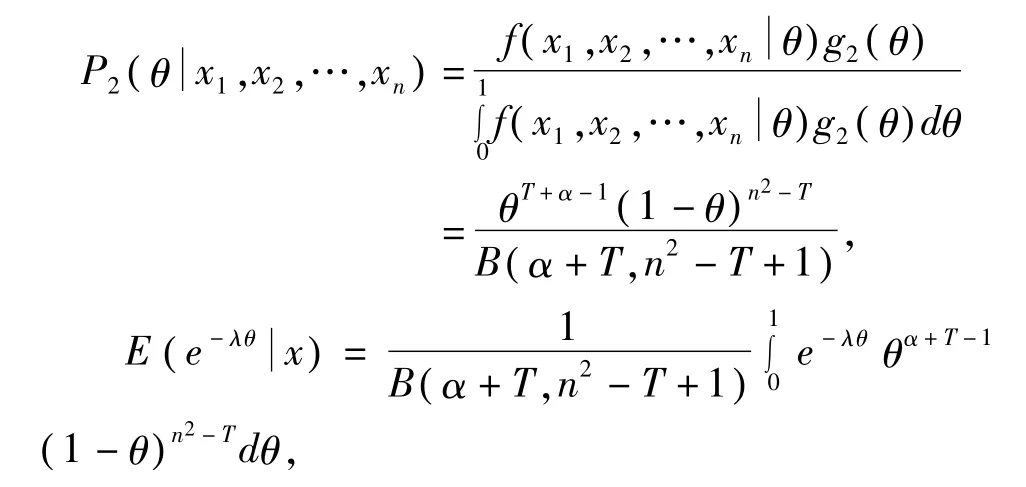
2 参数 θ的 Bayes估计的可容许性

为了证明参数θ的 Bayes估计的可容许性，下面给出一个引理。

引理2 在给定的Bayes决策问题中，假如对给定的先验分布 π (θ)，θ的 Bayes估计 δB(x)是唯一的，则它是容许估计。

定理3 对于参数θ任一先验分布，在 Linex损失函数下，参数θ的Bayes估计是可容许估计。

证明：由 Linex损失函数的表达式（3）可知该损失函数是关于 δ的凸函数，得参数 θ的Bayes估计必定是唯一的，由引理 2得 θ的 Bayes估计是可容许估计。

3 参数 θ的多层 Bayes估计

当 βa，( )b分布的超参数 a＞1且0＜b＜1时，Beta分布密度函数是参数 θ的增函数，a，b的先验分布分别取为

其中 c是一个常数，为了保证Bayes估计的稳健性，c的取值不宜过大。

通过下面的定理给出参数θ的多层 Bayes估计。

定理4 在Linex损失函数（3）下，对于第一层先验分布密度函数为（5）式，第二层先验分布为（8）式，二项分布参数 θ的多层 Bayes估计为

证明：由（5），（8）式得二项分布参数 θ的多层先验密度为

得 θ的后验概率密度函数为：

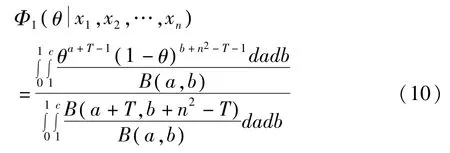
由（10）可计算出：

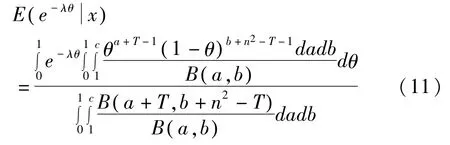
由（4）、（11）得参数 θ的多层Bayes估计为

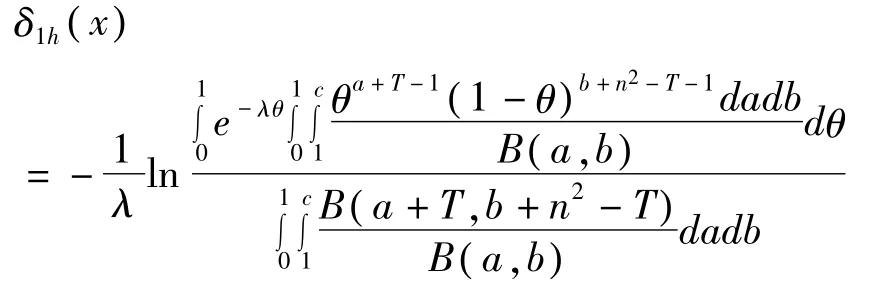
当 θ的先验分布为幂分布时，考虑到幂函数的性质及 Bayes估计的稳健性，α不宜过大，设其上界为 d，一般取 2≤d≤6，取超参数 α的先验分布为均匀分布

定理 5 在Linex损失函数（3）下，对于第一层先验分布为幂分布（7）式，第二层先验分布为（12）式，二项分布参数 θ的多层Bayes估计为

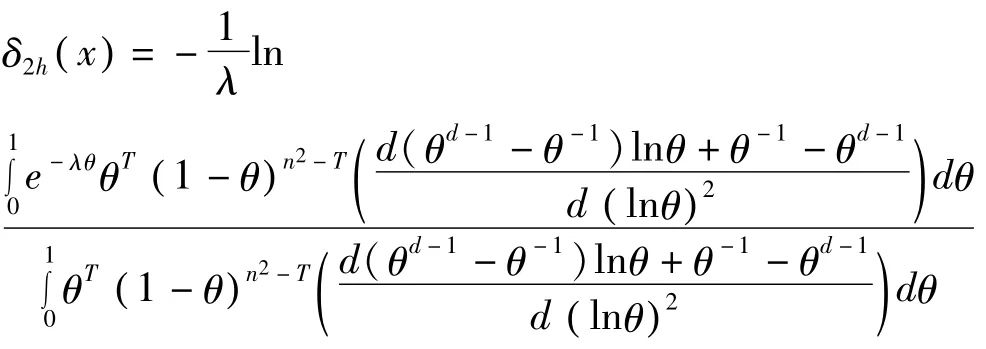
证明：由（7），（12）式得二项分布参数θ的多层先验密度为

得 θ的后验概率密度函数为：

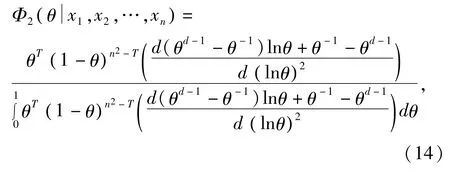
可计算出：

将（15）代入（4）式得参数 θ的多层 Bayes估计为

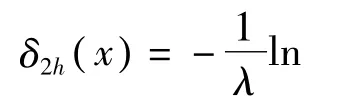
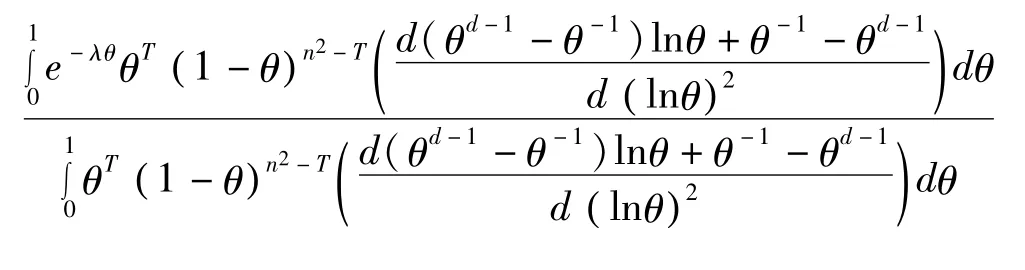
4 参数 θ的E－Bayes估计

为了给出参数θ的 E－Bayes估计的表达式，先给出 E－Bayes估计的定义。

定义［8］如果 δa，( )b是参数 θ的 Bayes估计，a，b为超参数，且 δa，( )b是连续的，则称

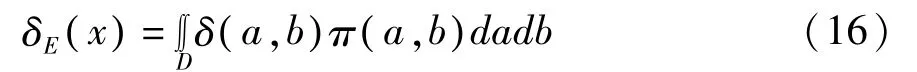
定理6 在Linex损失函数（3）下，二项分布参数 θ的先验分布为 Beta分布时，参数θ的 E－Bayes估计为

证明：由定理1可知参数θ的先验分布为 Beta分布时 θ的Bayes估计为

结合（8），（16）得参数θ的E－Bayes估计为

定理7 在Linex损失函数（3）下，二项分布参数 θ的先验分布为 Beta分布时，参数θ的 E－Bayes估计为

证明类似于定理 6。

［1］康会光，师义民.Linex损失下Pareto分布族参数的经验Bayes估计［J］.纯粹数学与应用数学，2001，17（2）：169－174.

［2］邓立凤，韦程东，苏韩.Linex损失下逆高斯分布参数倒数的Bayes估计［J］.上饶师范学院学报，2009，29（3）：15－18.

［3］陈志强，韦程东，韦莹莹.Linex损失下 Rayleigh分布参数倒数的 Bayes估计［J］.广西科学，2007，14（4）：362－364.

［4］刘荣玄，黄璇.在 Linex损失下指数分布刻度参数 EB估计的渐近最优性［J］.兰州理工大学学报，2009，35（2）：166－170.

［5］韦程东，韦师，陈志强.对称损失下二项分布参数的Bayes估计问题［J］.华中师范大学学报（自然科学版），2009，49（3）：367－372.

［6］康会光，赵小山，师义民.Linex损失下单边截断型分布族参数的EB估计［J］.应用数学，2001，14（3）：82－86.

［7］茆诗松，王静龙.高等数理统计学［M］.北京：高等教育出版社，1998：367－368.

［8］韩明.Pascal分布的参数估计［J］.纯粹数学与应用数学，2006，2（4）：510－514.

［责任编辑 贺小林］

The Bayesian Estimation of Binom ial Distribution Parameter Reciprocal Under Linex Loss

TAN LING
（School of Sciences，China University of Mining and Technology，Xuzhou 221116，China）

It discussed the Bayesian estimation of binomial distribution parameter under Linex loss function，given the precise form of Bayesian estimation，multi－layered Bayesian estimation and E－Bayesian estimation when prior distribution was taken to beta distribution and power distribution，finally，it proved the admissibility of Bayesian estimation.

Bayesian estimation；multi－layered Bayesian estimation；E－Bayesian estimation；the admissibility

O212.1

A

1004-602X（2011）02-0024-03

2011 -03 -19

谭玲（1987—），女，湖南湘潭人，中国矿业大学在读硕士研究生。