B－半强预不变凸函数及其性质

张文静，张庆祥

（延安大学 数学与计算机科学学院，陕西 延安 716000）

B－半强预不变凸函数及其性质

张文静，张庆祥

（延安大学 数学与计算机科学学院，陕西 延安 716000）

在 B－强预不变凸函数及半预不变凸函数的基础上定义了 B－半强预不变凸函数及其相关概念，并给出了一些性质。

B－半强预不变凸函数；半预不变凸函数；性质

凸性和广义凸性在数理经济、工程和最优化理论等方面发挥着巨大作用，因此，对凸性和广义凸性的研究是数学规划中最重要的内容之一。1981年，Hanson在文献［1］中提出了不变凸函数的概念，并得到了在不变凸性下 K－T条件是非线性规划问题有最优解的充分条件，这是一个非常重要的推广。1988年，Weir和 Mond在文献［2］中定义了一种广义凸函数，即预不变凸函数，并研究了它的性质以及在优化中的应用。1991年，Bector和 Singh在文献［3］中定义了 B－凸函数，讨论了它的一些性质。1993年，Bector等人在文献［4］中定义了B－不变凸函数，并讨论了B－凸函数和 B－不变凸函数的非线性规划最优解的充分条件及对偶性。1993年，Suneja等人在文献［5］中定义了B－预不变凸函数。2006年，余丽在文献［6］中定义了 B－强预不变凸函数，并得到了一些性质。1976年，Avriel在文献［7］中定义了半预不变凸函数。2003年，Yang等人在文献［8］中进一步讨论了半预不变凸函数的性质和它在多目标分式规划中的应用。

本文在 B－强预不变凸函数及半预不变凸函数的基础上定义了 B－半强预不变凸函数及其相关概念，并给出了一些性质。

注 如果 x，y∈Rn，那么我们规定

y＝z的⇔是：yi＝zi，i＝1，2，…，n

y＞z的⇔是：yi＞zi，i＝1，2，…，n

y≧z的⇔是：yi≧zi，i＝1，2，…，n

y≥z的⇔是：yi≧zi，i＝1，2，…，n；但至少存在一个1≦j0≦n，使 yi0＞zi0，即 y≠z。

1 预备知识

定义 1.1［11］设集合 K⊆Rn，如果存在一个向量函数 η：Rn×Rn×［0，1］→Rn，使得对∀x，y∈K，∀λ∈［0，1］，都有y＋λη（x，y，λ）∈K，则称集合K是关于 η的半不变凸集。

定义 1.2［7］设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，称 f在 y∈K点关于η为半预不变凸函数，若对∀x∈K及∀λ∈［0，1］，有f（y＋λη（x，y，λ））≤λf（x）＋（1－λ）f（y），且λη（x，y，λ）＝0.若对∀y∈K，f在y点关于η均为半预不变凸函数，则称f在 K上关于 η为半预不变凸函数。

定义 1.3［6］设集合 D⊆Rn是关于 η：Rn×Rn→Rn的不变凸集，称数量函数 f：D→R在 D上关于η，b是 B－强预不变凸函数，若存在一个常数β＞0，使得

其中 λb（x，y，λ）≥0，1－λb（x，y，λ）≥0，b（x，y，0）＝1＝b（x，y，1）。

2 主要结果

定义 2.1 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，称数量函数 f：K→R在 K上关于 η，b是B－半强预不变凸函数，若存在一个常数 β＞0，使得

其中 λb（x，y，λ）≥0，1－λb（x，y，λ）≥0，b（x，y，0）＝1＝b（x，y，1）。

定义 2.2 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，称数量函数 f：K→R在 K上关于 η，b是严格 B－半强预不变凸函数，若存在一个常数 β＞0，使得

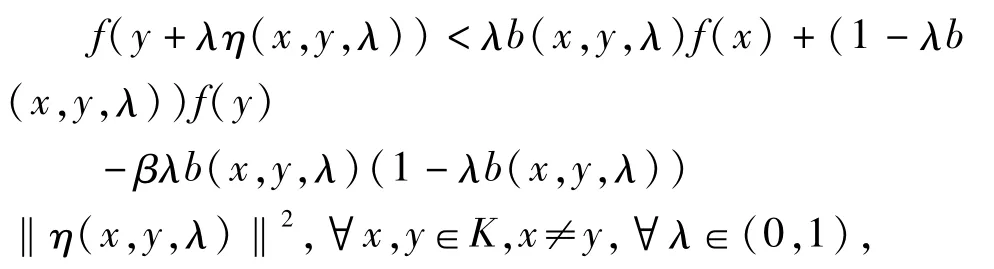
其中 λb（x，y，λ）≥0，1－λb（x，y，λ）≥0，b（x，y，0）＝1＝b（x，y，1）。

定义 2.3 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，称数量函数f：K→R在K上关于 η，b是半严格 B－半强预不变凸函数，若存在一个常数 β＞0，使得

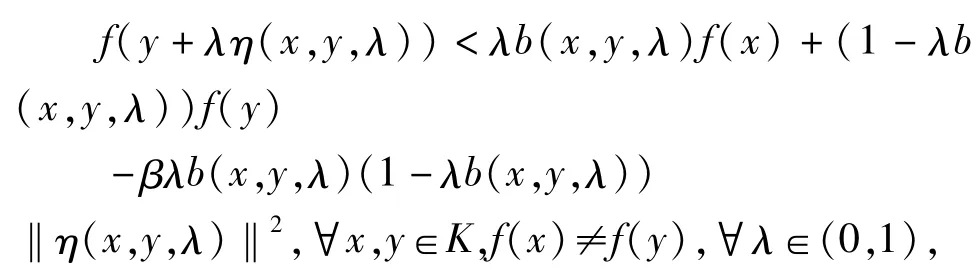
其中 λb（x，y，λ）≥0，1－λb（x，y，λ）≥0，b（x，y，0）＝1＝b（x，y，1）。

定理 2.1 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，若 f：K→R在 K上关于η，b是 B－半强预不变凸函数，k是任意常数，则 f＋k也是关于η，b的 B－半强预不变凸函数。

证明：因为f：K→R在K上关于η，b是B－半强预不变凸函数，故存在一个常数 β＞0，使得对∀x，y∈K，∀λ∈［0，1］，满足

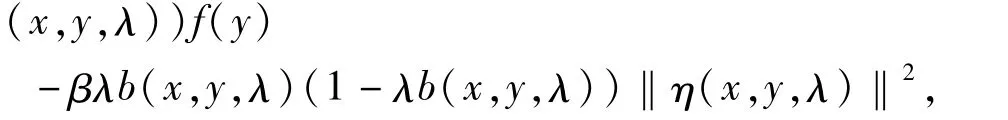
对上式两边同时加 k，于是有

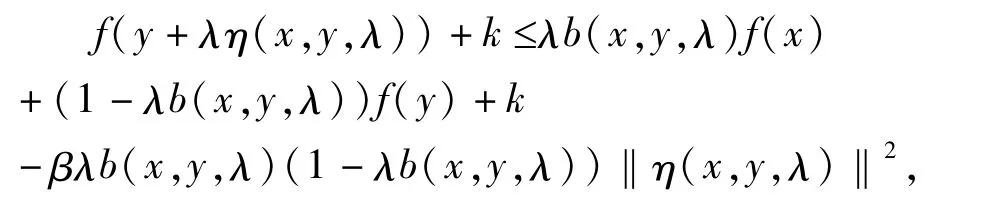
即

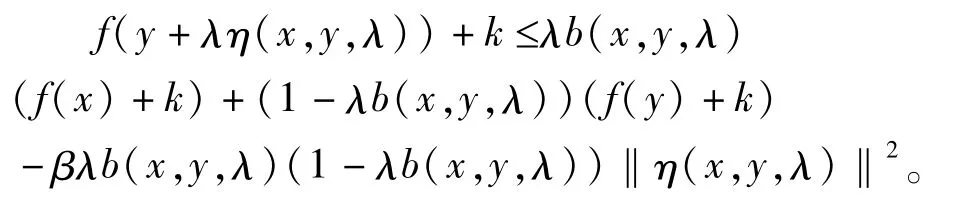
故f＋k也是关于η，b的B－半强预不变凸函数。

定理 2.2 设集合 K⊆Rn是关于η：Rn×Rn×［0，1］→Rn的半不变凸集，若f：K→R在K上关于η，b是 B－半强预不变凸函数，k＞0是任意常数，则kf也是关于 η，b的 B－半强预不变凸函数。

证明：因为 f：K→R在 K上关于 η，b是 B－半强预不变凸函数，故存在一个常数β＞0，使得对∀x，y∈K，∀λ∈［0，1］，满足

因为 k＞0，对上式两边同时乘以 k，得

又因为kβ＞0，故 kf也是关于 η，b的 B－半强预不变凸函数。

定理 2.3 设集合 K⊆Rn是关于η：Rn×Rn×［0，1］→Rn的半不变凸集，若fi：K→R（i＝1，2，…，p）在 K上关于 η，b是 B－半强预不变凸函数且在K上有上界，则函数f（x）＝max｛f1（x），f2（x），…，fp（x）｝在 K上关于 η，b是B－半强预不变凸函数。

证明：因为fi：K→R（i＝1，2，…，p）在K上关于η，b是 B－半强预不变凸函数，故存在一个常数 β＞0，使得对每一个i＝1，2，…，p，∀x，y∈K，∀λ∈［0，1］，满足

所以对每一个i＝1，2，…，p，有

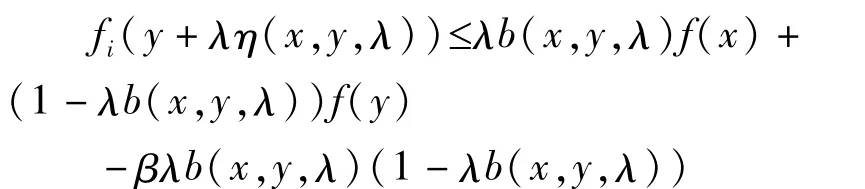
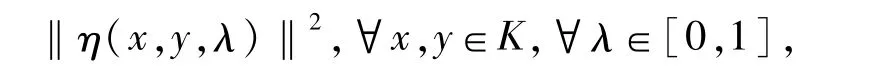
取上式左边的极大值，有

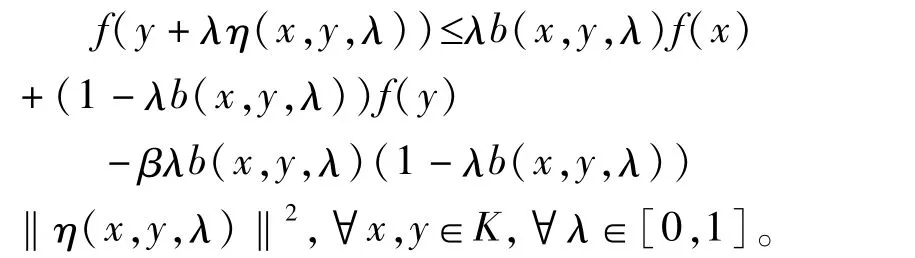
故 f在 K上也是关于 η，b的 B－半强预不变凸函数。

定理 2.4 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，若 fi：K→R（i＝1，2，…，p）在K上关于 η，b是半严格 B－半强预不变凸函数，则

f＝∑pi＝1kifi，∀ki＞0，i＝1，2，…，p，在K上关于η，b是半严格B－半强预不变凸函数。

证明：因为 fi：K→R（i＝1，2，…，p）在 K上关于η，b是半严格 B－半强预不变凸函数，故存在一个常数 β＞0，使得对∀x，y∈K，f（x）≠f（y），∀λ∈（0，1），有

因为对∀ki＞0，我们有

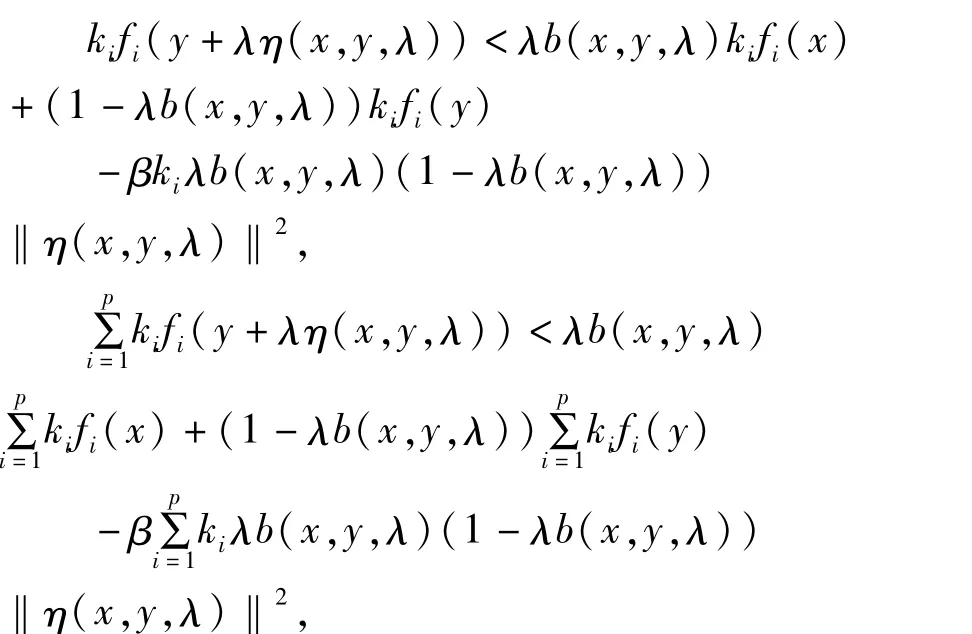
即

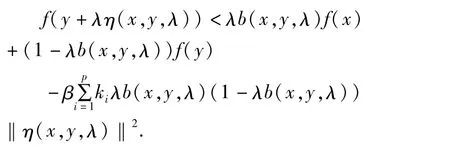
故 f在 K上也是关于 η，b的半严格 B－半强预不变凸函数。

定理 2.5 设集合 K⊆Rn是关于 η：Rn×Rn×［0，1］→Rn的半不变凸集，函数f：K→R在K上关于 η，b是 B－半强预不变凸函数，若是问题（P）的局部最优解，则也是问题（P）的整体最优解。

采用反证法，假设 x－不是问题（P）的整体最优解，则存在x*∈K，使得

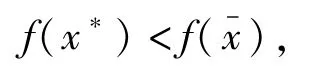
因为 K是半不变凸集，且f：K→R在K上关于η，b是B－半强预不变凸函数，则对∀λ∈［0，1］，有＋λη（x*，x－，λ）∈K，且

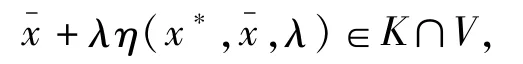
则（2）与（1）矛盾，故 x－也是问题（P）的整体最优解。

［1］Hanson M A.On sufficiency of Kuhn－Tucker conditions［J］.Journal of Mathematical Analysis and Applications，1981（80）：545－550.

［2］Weir T，Mond B.Pre－invex function in multiple objective optimization［J］.Journal of Mathematical Analysis and Applications，1988（136）：29－38.

［3］Bector CR，Singh C.B－Vex functions［J］.Journal of optimization Theory and Applications，1991（71）：237－254.

［4］Bector C R，Suneja K，Lalitha C S.Generalized B－Vex functions and generalized b－Vex programming［J］.journal ofOptimization Theory and Applications，1993（76）：561－576.

［5］Suneja SK，Singh C C.Bector R.Generalization of preinvex and B－vex functions［J］.Journal of Optimization Theory and Applications，1993（76）：577－587.

［6］余丽.B－强预不变凸函数［J］.宜春学院学报，2006（28）：7－8.

［7］Avriel M.Nonlinear programming：theory and methods［M］. New Jersey：Prentice，1976.

［8］Yang X M，Yang X Q，Teo K L.On properties of semipreinvex functions［J］.Bull Austral Math Soc.，1988（38）：177－189.

［9］林锉云，董加礼.多目标优化的方法与理论［M］.长春：吉林教育出版社，1992.

［10］秦春蓉.强预不变凸函数的性质［J］.重庆师范大学学报.2006，（23）：30－32.

［11］Yang X，Q，Chen G，Y.A Class ofnonconvex functions and prevariatinal inequa lities［J］.Journal of Mathematical Analysis and Applications，1992，（169）：359－373.

［责任编辑 贺小林］

B－strong Sem i－preinvex Functions and Its Properties

ZHANGWen－jing，ZHANG Qing－xiang
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

The definition and related concepts of B－strong semi－preinvex functionswas introduced on the basis of B－strong semi－preinvex functions and semi－preinvex functions，and some propertieswere concluded.

B－strong semi－preinvex functions；semi－preinvex funetions；poperties

O221.6

A

1004-602X（2011）02-0020-04

2011 -03 -28

陕西省教育厅专项科研基金资助课题（06JK152）

张文静（1985—），女，陕西延安人，延安大学在读硕士研究生。