三阶线性齐次微分方程的比较定理

周居政，秦宏立

（延安大学 数学与计算机科学学院，陕西 延安 716000）

三阶线性齐次微分方程的比较定理

周居政，秦宏立

（延安大学 数学与计算机科学学院，陕西 延安 716000）

在二阶线性微分方程 Sturm比较定理的基础上，利用 Picone恒等式，给出一类三阶线性齐次微分方程的 Sturm比较定理，所得结论推广了现有文献的结果。

三阶线性微分方程；Sturm比较定理；Picone恒等式；零点

0 引言

1836年瑞士数学家 Sturm首先提出了（p（t）x′（t））′＋q（t）x′（t）＝0的二阶线性齐次微分方程解的零点分布的Sturm分离定理和比较定理。此后，邓宗琦［1］研究了常微分方程边值问题 Sturm比较理论；庄荣坤等［2］研究了二阶非线性微分方程解的 Sturm比较定理；阎恩让［3］等讨论了二阶微分方程的比较定理；文献［4］中作者给出了三阶线性齐次微分方程解的Sturm比较定理。到目前为止，Sturm比较定理的数学思想不仅在二阶线性齐次微分方程和二阶线性非齐次微分方程中得到了发展和应用，甚至在高阶线性方程和非线性方程以及偏微分方程中都得到了发展和应用。本文考虑如下形式的三阶线性齐次微分方程（p（t）x″（t））′＋q（t）x′（t）＝0的Sturm比较定理。

1 预备知识

对如下形式的三阶线性齐次微分方程

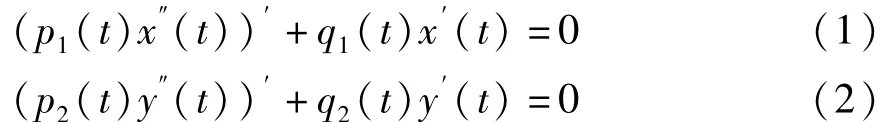
（此处 p1（t）≥p2（t）＞0，q1（t）≤q2（t），t∈［0，1］，p1（t），p2（t）∈C1（I），q1（t），q2（t）∈C（I），

I＝［0，1］）.

定义 1 设函数f（x）在解析区域D内一点a的值为零，则称a为解析函数 f（x）的一个零点。

定义2 设曲线 y＝f（x）在点（x0，f（x0））处有穿过曲线的切线，且在切点近旁，曲线在切线的两侧分别是严格凸和严格凹的，则称点（x0，f（x0））为曲线 y＝f（x）的拐点。

若对方程（1）式的两端同乘以 y′（t），对方程（2）式的两端同乘以 x′（t），便有

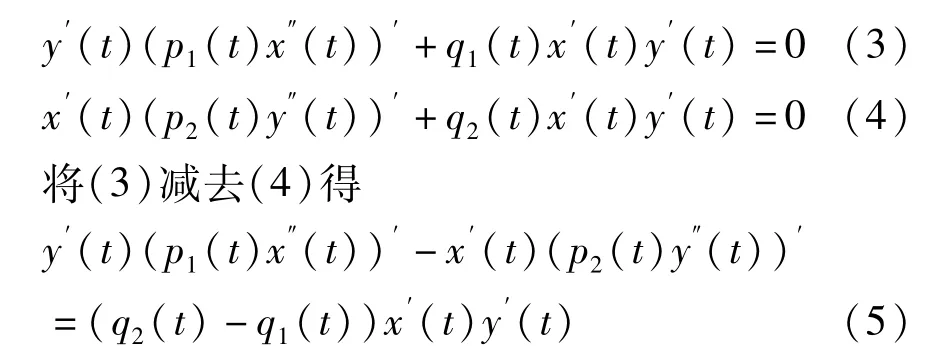
由于，（5）式的左端可以写为

从而，上述（5）式便可改写作

若对（6）式两端从0到1积分便得到

由于上式右端的第二个积分中有x″（t）y″（t）的因子。于是，由二阶 Picone恒等式的启发，我们有下列引理。

引理 设x（t）与y（t）分别是方程（1）与（2）的非平凡解，且 α，β∈I是 x（t）的两个相邻零点，x′（t）与y′（t）分别是方程（1）与（2）的非平凡解的导函数，若y′（t）≠0，t∈（α，β），则在［α，β］上成立恒等式

证明

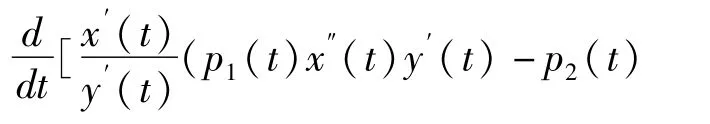
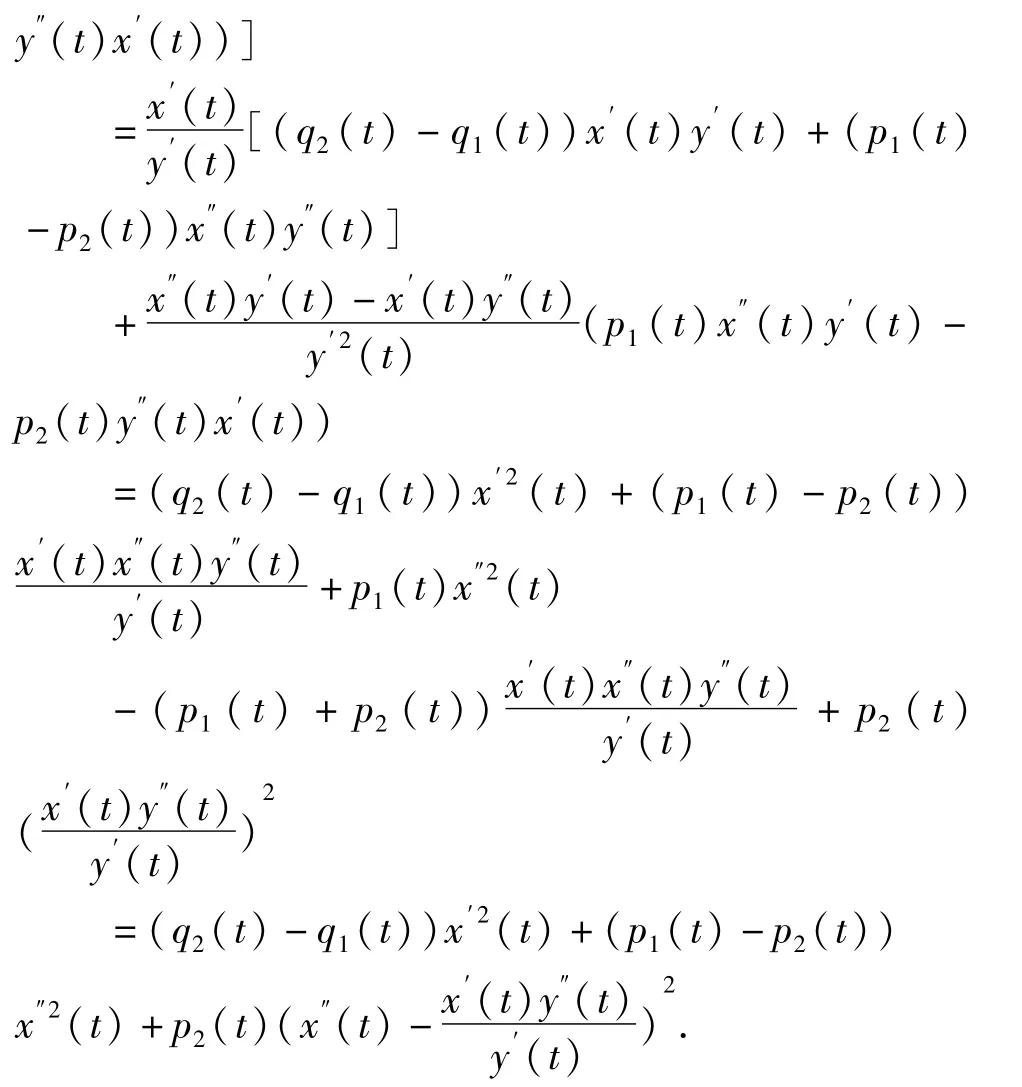
2 主要结果

定理 设方程（1）和（2）中的 p1（t），p2（t）∈C1（I），q1（t），q2（t）∈C（I），I＝［0，1］；又设方程（1）式的非平凡解x（t）的导函数 x′（t）的两个相邻零点为 α，β∈I，且 α，β为x（t）的拐点；如果

（i）p1（t）≥p2（t）＞0；

（ii）q1（t）≤q2（t），t∈I.则方程（2）式的每个解 y（t）的导函数 y′（t）在［α，β］上至少有一个零点。

证明 假设y′（t）在［α，β］上没有零点.可以令t∈（α，β）；x′（t）＞0，y′（t）＞0，

则对（7）式从α到β积分得到

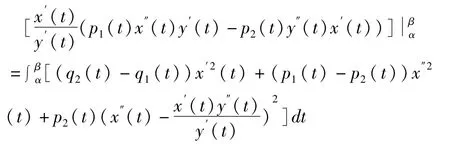
即

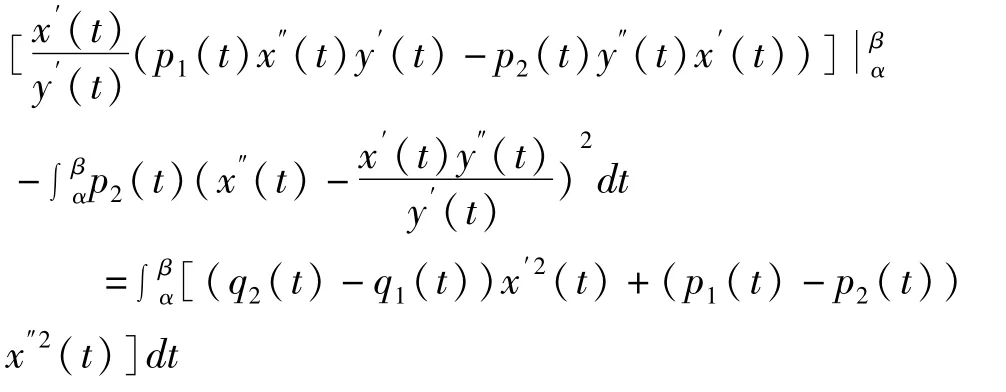
由于α，β∈I是x′（t）的零点，即x′（α）＝x′（β）＝0；而p2（t）＞0，于是有

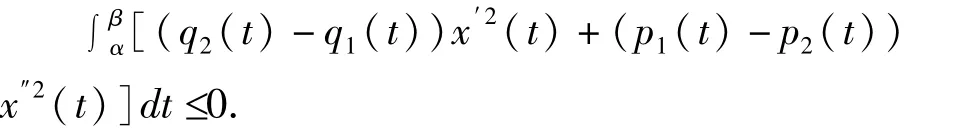
由此引出矛盾；除非p1（t）≡p2（t），q2（t）≡q1（t），此时就有

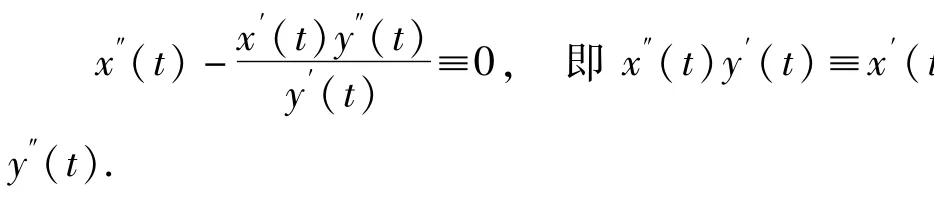
因此，x′（t）＝y′（t），即y′（α）＝y′（β）＝0，这又与假设相矛盾。

故定理得证。

［1］邓宗琦.常微分方程边值问题Sturm比较理论引论［M〛.武汉：华中师范大学出版社，1990.

［2］庄荣坤.二阶非线性微分方程解的导函数的 Sturm比较定理［J］.工程数学学报，2001（1）：131－134.

［3］阎恩让，王霞.二阶微分方程的比较定理［J］.宝鸡文理学院学报（自然科学版），1998（4）：14－17.

［4］薛巧梅，秦宏立，张荣荣.三阶线性齐次微分方程解的Sturm比较定理［J］.榆林学院学报，2009（4）：18－19.

［责任编辑 贺小林］

Third Order Linear Homogeneous Differential Com parison Theorem

ZHOU Ju－zheng，QIN Hong－li
（College of Mathematics and Computer Science，Yan an University，Yan an 716000，China）

In the second order linear differential equation Sturm comparison theorem＇s foundation，by using the picone identical equation＇s，a kind of third order linear homogeneous differential equation was given the Sturm comparison theorem.Some resultswere generalized.

third order linear homogeneous differential equation；sturm comparison theorem；picone identical equation＇s inspiration；zero point

O175.11

A

1004-602X（2011）02-0018-02

2011 -03 -28

周居政（1985—），男，陕西渭南人，延安大学在读硕士研究生。