一种提高内存使用效率的时域有限差分算法

张 品 陈亦望 傅 强

（解放军理工大学工程兵工程学院，江苏 南京 210007）

1.引 言

时域有限差分方法（FDTD）已经广泛应用于电磁散射计算领域［1－3］。然而，传统FDTD方法所需计算资源量非常大，并且受到CFL稳定条件的限制，使得计算效率不高，计算时间较长，这一切都给使用FDTD方法进行电磁仿真计算带来困难。为了突破CFL稳定条件的限制，Takefumi Namiki提出了交替隐式时域有限差分法（ADI－FDTD）［4－5］，提高了计算速度，但是计算公式较为复杂，占用内存较大。近来，J.Shibayama等人提出的局部一维时域有限差分法（LOD－FDTD）也被应用到电磁计算中［6－7］。由于 LOD－FDTD 方法比 ADI－FDTD 方 法的计算公式简单，占用内存较少，计算效率得到提升［6］。

虽然LOD－FDTD方法摆脱了CFL条件限制，具有更高的计算效率，但是由于其求解过程中仍然需要解方程组，所以LOD－FDTD方法计算所需内存量依然比传统FDTD方法要大，相对有限的计算机资源给LOD方法的应用带来了制约。

减缩时域有限差分法（R－FDTD）是一种有效减少内存使用量的方法［8］。R－FDTD方法依据麦克斯韦方程组中三个电场方程与三个磁场方程之间通过散度方程建立的相互联系，避免了部分场量值的存储，使得原本需要储存的麦克斯韦方程组6个方程量减少为4个方程量。循环使用一维数组储存场量代替二维数组储存（二维情况），或二维数组代替三维数组储存（三维情况），这样就达到了平均节约33%内存的目的［8－9］。

在文献［9］中，R－FDTD已经用于改进二维ADI－FDTD方法，但该文假设在无源区电场或磁场仍为零散度关系，这将导致大时间步长计算时计算的发散。不同于利用传统FDTD计算时电、磁场分量散度关系为零，经过研究发现，在无源场区环境下利用局部一维时域有限差分法（LOD－FDTD）计算时，电、磁场分量的散度非零，并推导了该散度关系的具体表达式。基于此散度关系，提出一种新的时域有限差分方法——局部一维减缩时域有限差分法（LOD－R－FDTD），并给出了具体计算格式。该方法使电、磁场的计算不仅能够摆脱CFL条件限制、减少计算时间，而且节省平均达1／3的内存使用量。通过数值仿真实验证明了新方法的准确性和有效性。

2.LOD－FDTD计算时电、磁场分量的空间散度

仅考虑二维TE波模型，但是同样可以推广到三维情况［10－11］。

2.1 二维TE波LOD－FDTD公式推导

对于二维TE波情况，有Ez＝Hx＝Hy＝0。Maxwell方程组在各向同性、无损耗介质空间的形式为

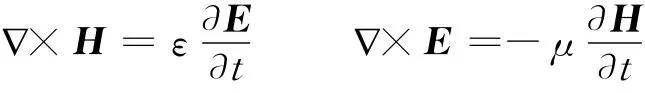
在直角坐标系中可表示为

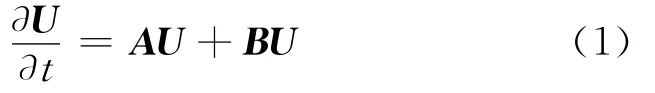
式中U＝ ［Ex，Ey，Hz］T；

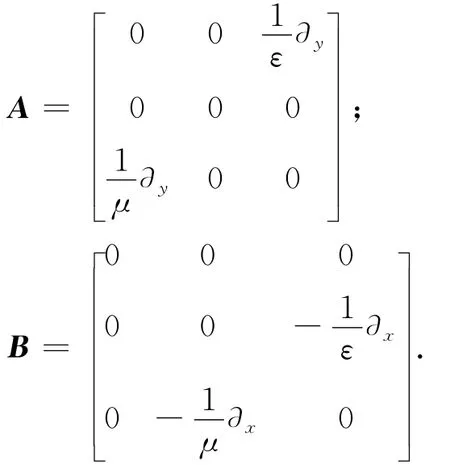
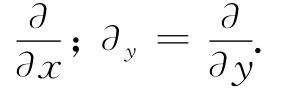
对式（1）应用近似：（∂U）／∂t≈ （Un＋1－Un）／Δt，Un＋（1／2）≈ （Un＋1＋Un）／2，得到Crank－Nicolson形式

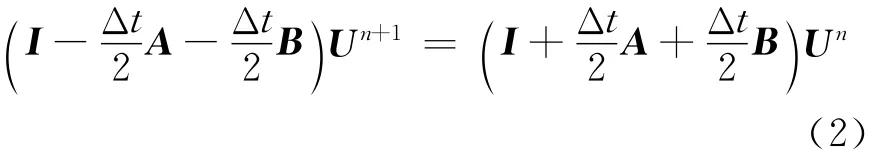
式中I为单位矩阵。式（2）近似表示为

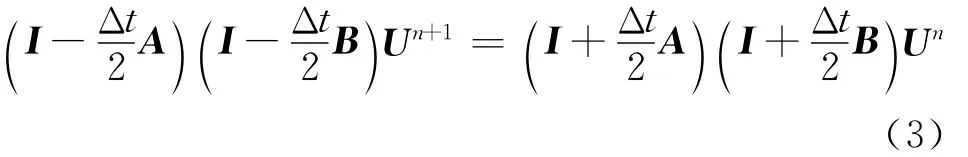
式（3）可通过两个时间步骤进行计算：

子时间步1：n→n＋1／2

子时间步2：n＋1／2→n＋1

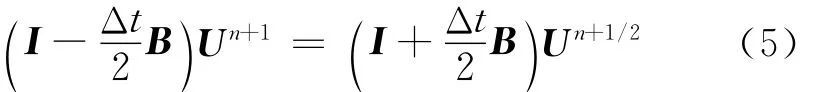
将各场分量代入式（4）和（5）得到

子时间步1：n→n＋1／2

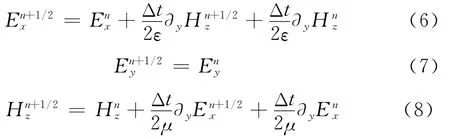
子时间步2：n＋1／2→n＋1

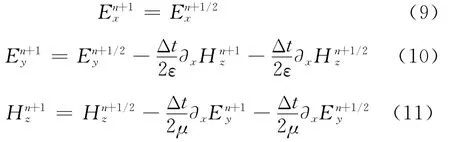
文献［12］已证明，以上方法无条件稳定。

2.2 LOD－FDTD计算时的电、磁场分量空间非零散度关系

基于经典电磁场计算理论，在无空间电荷的区域电、磁场散度为零［8］，即

将传统FDTD Yee's各场量计算式代入式（12）、（13），可证明当电、磁场的各场量采用传统FDTD格式计算时，式（12）、（13）的空间离散形式成立。但是，当采用 LOD－FDTD 法计算时，式（12）、（13）的空间离散形式不再成立。下面以TE波为例，推导LOD－FDTD算法下电、磁场分量的空间散度关系。

在时间步n＋1／2时，

对于电场散度有

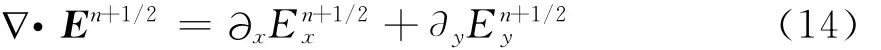
将式（6）和（7）代入式（14），有

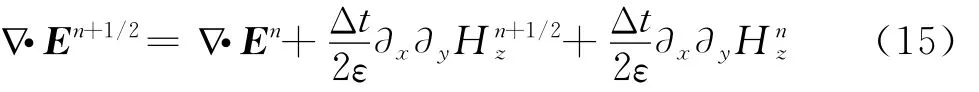
假设在n＜0的时间步，各场分量均为零，得到电场空间散度关系为

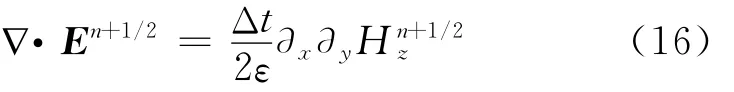
在空间网格（i，j）处，n＋1／2时间步的Ey由式（16）计算，具体形式为

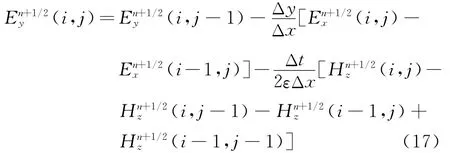
在时间步n＋1时，

对于电场散度有

将式（9）和（10）代入式（18），有

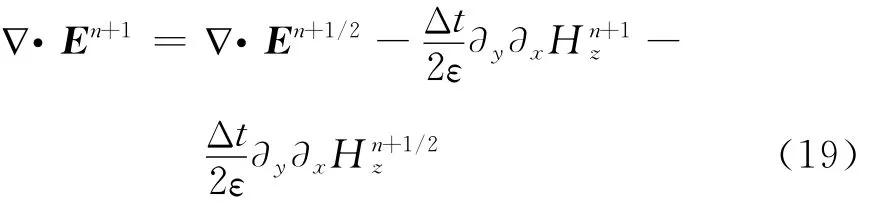
将式（16）代入式（19），得到电场空间散度关系为

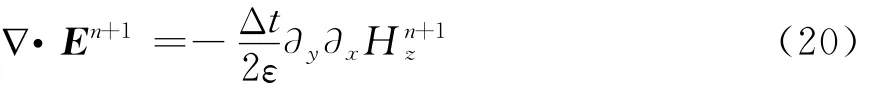
在空间网格（i，j）处，n＋1时间步的Ex由式（20）计算，具体形式为

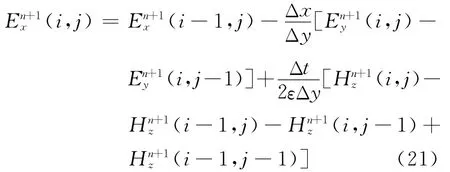
同理，对于二维TM波可得到类似的电、磁场散度的空间表达形式。

2.3 LOD－FDTD与R－FDTD结合

在二维情况下以TE波为例，设计算区域为Nx×Ny的无电荷矩形空间区域。采用LOD－FDTD计算时，所计算场量为Ex、Ey和Hz三个分量。在n＋1／2和n＋1时间步共需6个二维数组存储整个计算区域的分量值。将LOD－FDTD与R－FDTD结合，应用非零散度关系式，在n＋1／2时间步，在整个计算区域存储Ex、Hz分量，不在整个计算区域存储Ey分量，而仅用一维数组（i）循环存储j＝c（c＝1，…，Ny）的网格上的Ey分量；在n＋1时间步，在整个计算区域存储Ey、Hz分量，不在整个计算区域存储Ex分量，而仅用一维数组（j）循环存储i＝c（c＝1，…，Nx）的网格上的Ex分量。这样一来，仅需要4个二维数组存储整个计算区域的分量值，LOD－R－FDTD方法所需内存仅为 LOD－FDTD 所需内存的2／3。

理论上可以任意选定一个电场量不使用二维数组存储其在整个计算空间的数值，而是利用非零散度关系式（式（16）、（20））得到某个计算列上的数值，并存储在一维数组中，在随后的计算过程中沿着与此计算列垂直的方向循环更新。但是，如果在计算区域中选定空间距离最长的方向作为一维数组更新方向，则可以最大程度地节约内存。

仍以二维 TE波情况为例。使用 LOD－RFDTD算法，选定（i）、（j）两个分量不需要使用二维数组储存所有计算空间的场值，而仅需要一维数组储存分别沿x轴、y轴方向上不断更新的场值和.为了更清晰地描述该算法的计算过程，具体算法的伪代码见图1。

3.试 验

为了评估LOD－R－FDTD方法的有效性和准确性，本文采用提出的LOD－R－FDTD方法分别计算TE波的二维自由空间和三维自由空间传播情况，并将计算结果与传统FDTD以及LOD－FDTD方法的计算结果相比较。

3.1 二维TE波波导模型

平行波导模型如图2（a）所示。波导的两平行表面均为理想电导体（PEC边界条件）。在波导两端使用8层完美匹配层（PML吸收层）。计算空间共划分为75×20的网格，在自由空间网格大小为1.0mm×1.0mm.波导内有两个带有狭缝的薄膜层。电介质薄膜厚度为0.5mm，εr＝2.0，μr＝2.0，σ＝15.0S／m.狭缝宽度为0.3mm.薄膜处的网格大小为0.1mm×0.1mm.

使用传统FDTD方法时，由于CFL条件的限制，时间步长设为0.23ps.当使用LOD－FDTD和LOD－R－FDTD方法时，时间步长设为3.33ps.设左端电场垂直分量为激励源，右端电场垂直分量为输出信号观察点。激励脉冲波方程为

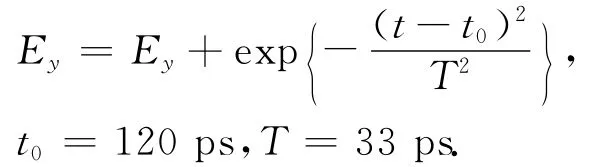
观察点处的振幅归一化输出信号如图2（b）所示。观 察 可 知 LOD－FDTD、LOD－R－FDTD 与 传 统FDTD方法的计算结果符合较好。LOD－R－FDTD与LOD－FDTD方法计算结果一致，说明LOD－RFDTD方法继承了LOD－FDTD的准确性。表1提供了不同方法仿真计算时使用计算资源的比较。使用LOD－R－FDTD 和 LOD－FDTD 方法的时间步长均为传统FDTD方法的5倍，dtLOD－R＝5dt.比较后可发现，使用LOD－R－FDTD方法的CPU计算时间降低为传统FDTD方法的72.7%。LOD－R－FDTD方法使用的内存为LOD－FDTD方法的78.9%。比较 结 果 表 明：LOD－R－FDTD 方 法 继 承 了 LODFDTD方法大时间步长的优点，减少了计算时间；同时也继承了R－FDTD方法的优点，大大减少了计算所需内存。

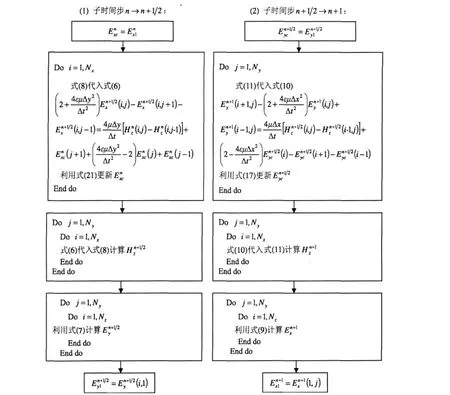
图1 LOD－R－FDTD算法伪代码

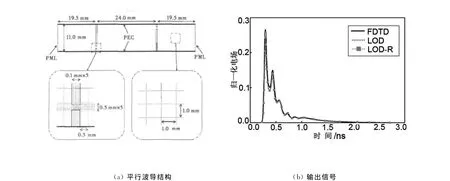
图2 二维TE波模型及计算比较

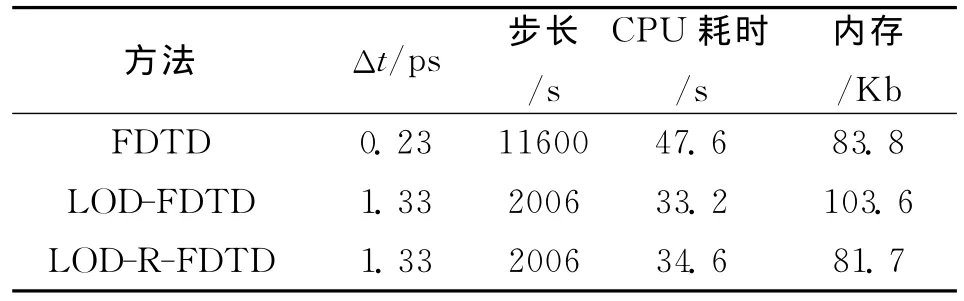
表1 不同算法间比较

3.2 三维计算模型

计算一个2cm×1cm×2cm的矩形真空腔体，网格设为Δx＝Δy＝Δz＝1mm，将计算空间划分为20×10×20个网格。时间步dtLOD－R＝5.8dtCFL.仿真时间长度为8000时间步。在4个腔体壁处采用8层PML吸收边界。图3为原始FDTD、LODFDTD和LOD－R－FDTD的时域电场波形。

由图3（a）可以看到：LOD－R－FDTD 方法是无条件稳定的。由图3（b）可知，LOD－R－FDTD方法与其他方法的计算结果具有较好的一致性。本例计算中 LOD－R－FDTD 计算所用内存比 LOD－FDTD计算所用内存节约了13.7%。

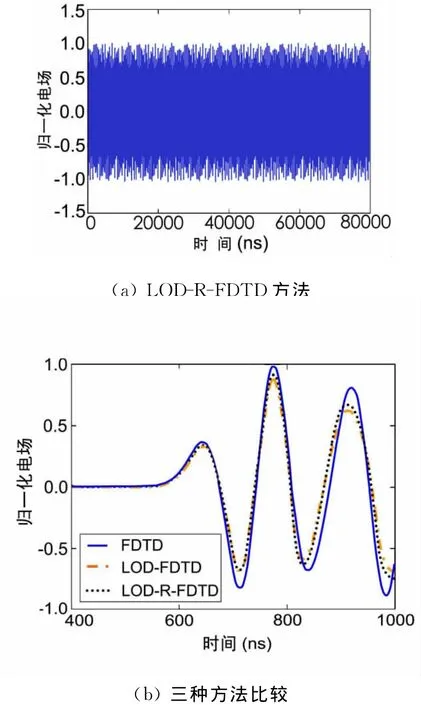
图3 电场时域图像

4.结 论

本文证明了即使在无源区域，局部一维时域有限差分方法（LOD－FDTD）的电、磁场量也不满足零散度关系，同时推导了该散度关系的具体表达式。基于推导出的非零散度关系，提出了一种新的局部一维缩减时域有限差分方法（LOD－R－FDTD），并给出了具体计算公式。通过二维、三维问题的实验计算，证明该方法不仅保留了LOD－FDTD的无条件稳定性、增大了时间步长、减少了总计算时间，而且使计算所需内存比LOD－FDTD减少平均可达1／3。该方法与LOD－FDTD的计算结果一致，具有良好的计算稳定性。提出的新方法可用于计算区域较大、计算内存相对有限的电磁计算问题。

［1］SINGH G，TAN E L，CHEN Z N.A split－step FDTD method for 3－D Maxwell’s equations in general anisotropic media［J］.IEEE Transactions on Antennas and Propagation，2010，58（11）：3647－3657.

［2］汤 炜，李清亮，焦培南，等.ADI－FDTD在二维散射问题中的应用［J］.电波科学学报，2003，18（6）：620－624.

TANG Wei，LI Qingliang，JIAO Peinan，et al.Twodimension scattering analysis using ADI－FDTD method［J］.Chinese Journal of Radio Science，2003，18（6）：620－624.（in Chinese）

［3］黄斌科，蒋延生，汪文秉.二维无条件稳定时域有限差分方法［J］.电波科学学报，2003，18（5）：534－539.

HUANG Binke，JIANG Yansheng，WANG Wenbing.Two－dimensional unconditionally stable FDTD method［J］.Chinese Journal of Radio Science，2003，18（5）：534－539.（in Chinese）

［4］NAMIKI T.A new FDTD algorithm based on alternating－direction implicit method［J］.IEEE Transactions on Microwave Theory and Techniques，1999，47（10）：2003－2007.

［5］ROUF H K，COSTEN F，GARCIA D G.Reduction of numerical errors in frequency dpendent ADI－FDTD［J］.IEEE Electronics Letters，2010，46（7）：489－490.

［6］SHIBAYAMA J，MURAKI M，YAMAUCHI J，et al.Efficient implicit FDTD algorithm based on locally one－dimensional scheme［J］. Electronics Letters，2005，41（19）：1046－1047.

［7］TAN E L.Acceleration of LOD－FDTD method using fundamental scheme on graphics processor units［J］.IEEE Microwave and Wireless Components Letters，2010，20（12）：648－650.

［8］KONDYLIS G D，FLAVIIS F D，POTTIE G J，et al.A memory－efficient formulation of the finite－difference time－domain method for the solution of Maxwell equation［J］.IEEE Trans.MTT，2001，（7）：1310－1320.

［9］LIU B，GAO B Q，TAN W，et al.A new FDTD Aalgorithm－ADI／R－FDTD［C］／／Electromagnetic Compatibility，2002 3rd International Symposium on，May 21－24，2002，IEEE 0－7803－7277－8／02：250－253.

［10］AHMED I，CHUA E K，LI E P，et al.Development of the three－dimensional unconditionally stable LODFDTD method［J］.IEEE Transactions on Antennas and Propagation，2008，56（11）：3596－3600.

［11］TANE L.Unconditionally stable LOD－FDTD method for 3－D Maxwell’s equations［J］.IEEE Microw.Wireless Compon.Lett.，2007，17（12）：85–87.

［12］刘国胜，张国基.高阶LOD－FDTD方法的数值特性研究［J］.电子与信息学报，2010，32（6）：1384－1387.

LIU Guosheng，ZHANG Guoji.Study for the numerical properties of the higher－order LOD－FDTD methods［J］.Journal of Electronics ＆ Information Technology，2010，32（6）：1384－1387.（in Chinese）