最高可用频率自适应预报算法研究

徐 彬 吴永宏 刘毅敏

（1.海军电磁频谱管理办公室，北京100841；2.中国电波传播研究所，山东 青岛266107）

1.引 言

最高可用频率指实际通信中能被电离层反射回地面的电波的最大频率[1]，若选用的工作频率超过它，则电波穿出电离层，不再返回地面；若选用的工作频率太低，电波传输损耗较大，通信效果较差[2]。将工作频率选定在最高可用频率附近通常会带来较好的通信效果[3]，因此预报最高可用频率对短波通信系统合理选取工作频率具有重要的意义。

通常，可以基于电离层模式进行最高可用频率的长期预报[4－6]，也可以基于电离层实际测量数据进行最高可用频率的短期预报。Zolesi等人利用有效太阳黑子数代替R12，进而确定F2层临界频率f0F2，然后结合电离层传播因子 M（3000）F2对链路的最高可用频率进行短期预报[7－10]。Pietrella等人 提 出 了ISWIRM 模 型 （Instantaneous Space Weighted Ionospheric Regional Model），该模型利用欧洲地区的4个探测站的实时数据预报F2层临界频率f0F2，仅适用于北纬35°到70°西经5°到东经40°所覆盖的区域[11]。黄德耀[12]和张训械[13]分别采用线性相关和神经网络方法预报最高可用频率。

Kalman滤波技术作为一种数学工具，从1960年提出以来得到了快速发展，在卫星导航、飞行器控制、数据通信等领域得到了广泛应用[14－17]。为了根据链路当前时刻的探测数据预报未来时刻的最高可用频率，本文在前人工作的基础上引入了Kalman滤波技术，设计了最高可用频率自适应预报算法，并用中国电波观测网的实测数据对该算法的性能进行了检验，取得了较好的效果。

2.Kalman滤波技术[9]

Kalman滤波模型用状态空间来描述数学公式，而且它的解也是递归计算的，可以不加修改地应用于平稳和非平稳环境，其状态方程为

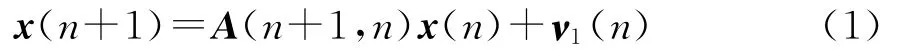
式中：x（n）为M×1维状态向量；A（n＋1，n）为M×M维转移矩阵；ν1（n）为M×1维高斯白噪声；n表示时刻。

测量方程为

式中：y（n）为N×1维系统输出向量；C（n＋1，n）为N×M维测量矩阵；ν2（n）为N×1维高斯白噪声；n表示时刻。

令Yn为y（1），y（2），…，y（n）张成的空间，新息α（n）＝y（n）－（n｜Yn－1），状态预测误差向量为ε（n，n－1）＝x（n）－（n｜Yn－1），Q2（n）为测量噪声向量ν2（n）的相关矩阵，Q1（n）为状态噪声向量ν1（n）的相关矩阵，状态预测误差相关矩阵为K（n，n－1）＝E[ε（n，n－1）εH（n，n－1）] ，对式（1）和（2）进行推导，可得状态向量的估计值为

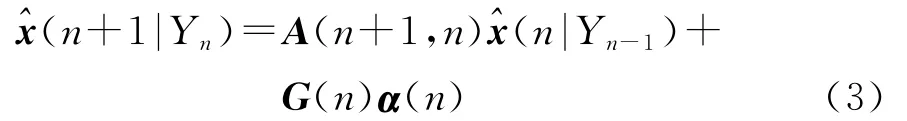
式中Kalman增益矩阵为

其中

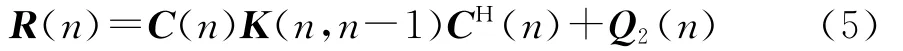
利用Riccati差分方程可得状态预测误差相关矩阵的递归计算表达式为

式中

通过分析式（1）～（7），可以看出转移矩阵A（n＋1，n）、测量矩阵C（n＋1，n）、测量噪声相关矩阵Q2（n）、状态向量噪声相关矩阵Q1（n）是已知的，配置好初始条件＾x（1｜Y0）、K（1，0）即可利用式（3）～（7）进行递归计算，估算状态向量x（n）。

3.最高可用频率自适应预报

电离层斜向探测设备每半个小时测量到一幅电离图，从该电离图可以读出最高可用频率，把读出的最大可用频率按时间进行排序，就形成了一个时间序列，实践证明该序列是一个平稳随机过程。因此，可以根据电波观测网测量的已知数据预报特定链路在未来时刻的最高可用频率。

若最高可用频率观测数据用y（n）来表示，利用平稳时间序列自回归模型可得

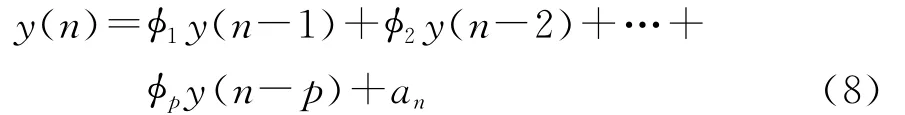
式中：φ1，φ2，…，φp为待定系数；an为高斯白噪声。

令Y（n－1）＝[y（n－1），y（n－2），…，y（n－p）] ，φ（n－1）＝[φ1，φ2，…，φp]T，则式（8）可变为

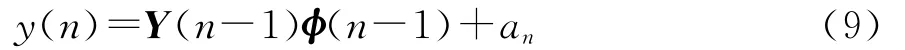
而且

将式（9）、（10）和式（1）、（2）进行对比，可得

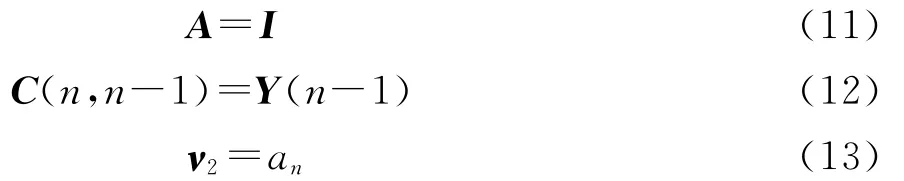
把式（11）～（13）代入式（3）～（7），可得这样式（14）～（17）就构成了递归求解算法，其计算流程如图1所示，图中测量噪声相关矩阵Q2和测量数据y（n）为已知参数（0）、K（0）为递归初始条件。也就是说，通过递归计算可以获得较为准确的向量＾φ（n），那么未来时刻最高可用频率的预测值为

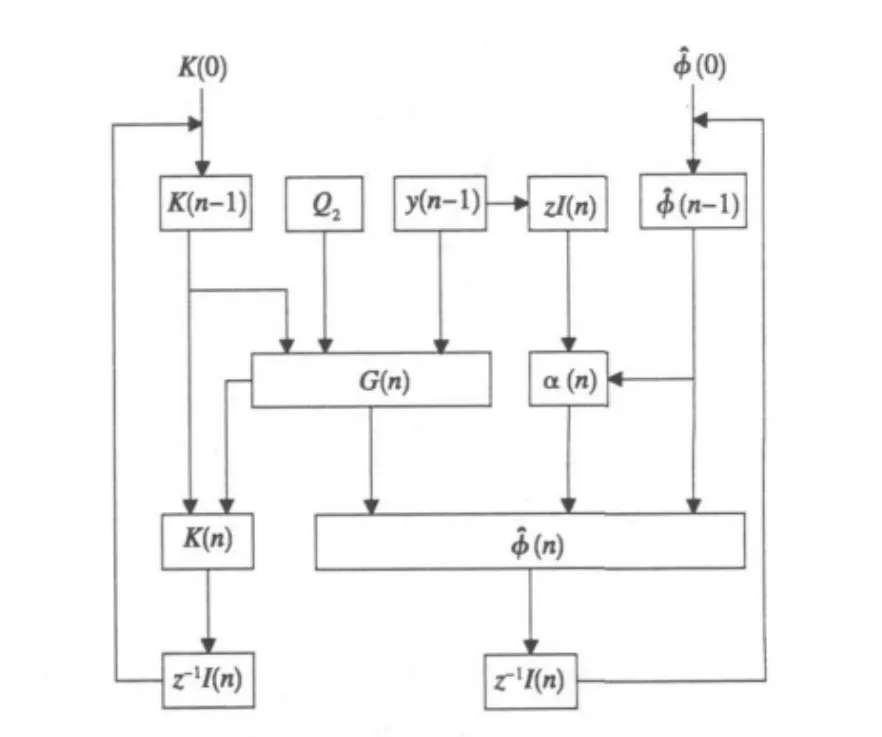
图1 自适应预报算法流程

把上述算法称为自适应预报算法，该算法可以根据实际测量数据的变化自动修正自回归模型的待定系数，然后对未来时刻的最高可用频率进行预报。

4.实测数据检验

我们收集了2010年5月到2010年10月中国电波观测网电离层斜向探测设备测量的北京－青岛链路电离图，从这些图中读取最高可用频率，然后用这些实测数据对自适应预报算法的性能进行检验。

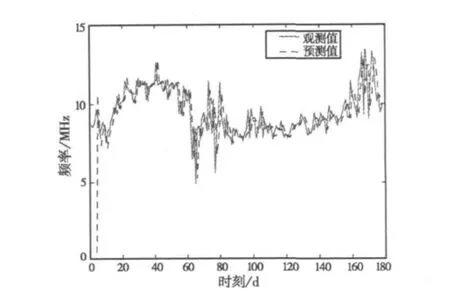
图2 自适应预报算法跟踪过程

令p＝2，测量误差相关矩阵Q2＝1，＾φ（0）＝[1，，利用自适应预报算法给出的结果如图2所示，图中直线为2010.5～2010.10期间每日13点对应的最高可用频率的观测值，点线为预报值，可以看出，自适应预报算法在第12个数值点附近就跟踪上了观测值，而且随后较准确地重现了观测值。

定义预报误差的均方差为

式中：i为预报值下标；N为预报值总数量；e（i）为预报相对误差，其表达式为

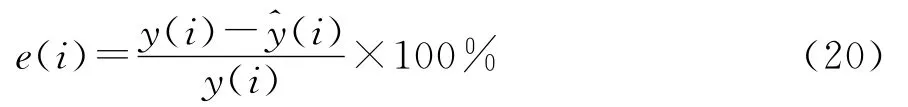
且y（i）为观测值（i）为预报值。

表1为根据自适应预报算法给出的一天中每个小时预报误差的均方差，表2为根据中国参考电离层模型给出的一天中每个小时预报误差的均方差，图3为这两个均方差的图形化显示。可以看出，与长期预报算法相比，基于实测数据的自适应预报算法可以给出更精确的结果。

表1 自适应预报算法给出的均方差

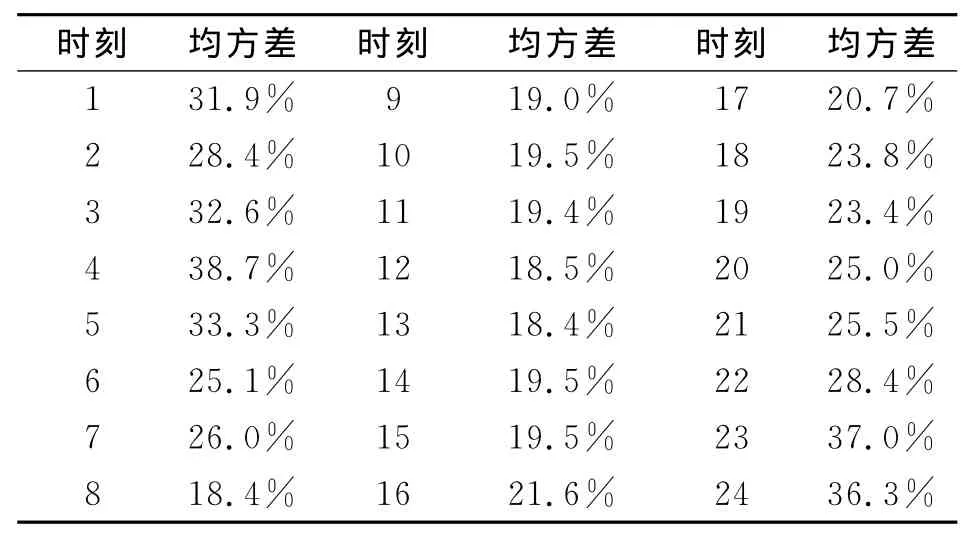
表2 长期预报算法给出的均方差

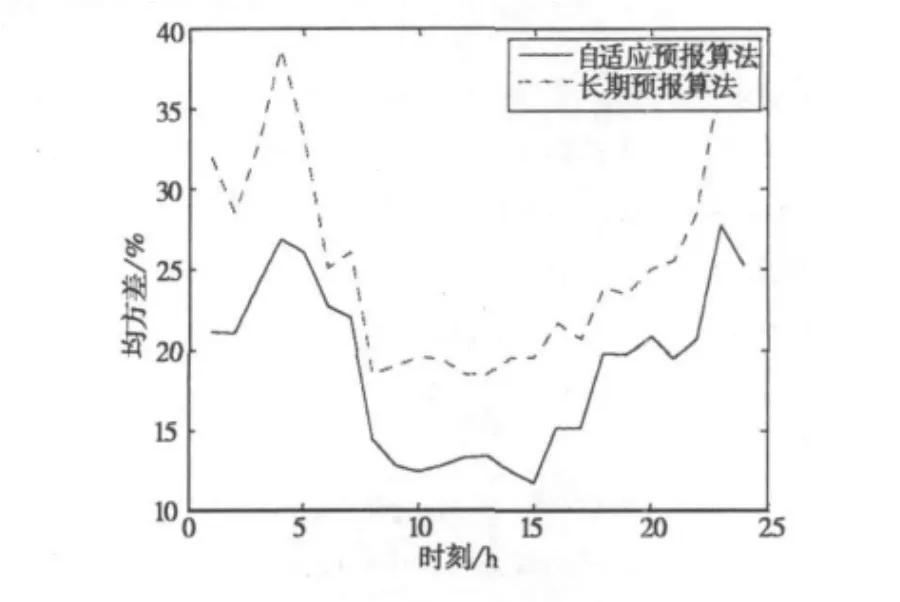
图3 一天中均方差变化曲线

5.结 论

本文从短波通信系统和短波链路需要预报或指配优质频率的工程实际出发，引入了Kalman滤波技术和最高可用频率观测数据自回归模型，利用Kalman滤波技术推导自回归模型中待定系数的求解方法，进而给出了最高可用频率自适应预报算法。利用中国电波观测网测量的北京－青岛链路数据对该算法的性能进行检验，结果表明最高可用频率自适应预报算法能够从人为设定的初值较快跟踪上自回归模型的待定系数，此后基于实际观测数据较准确地预报了未来时刻的最高可用频率，其预报误差的均方差远低于中国参考电离层模型给出的结果。

[1] 沈琪琪，朱德生.短波通信[M] .西安：西安电子科技大学出版社，1989.

[2] 熊年禄，唐存琛，李行健.电离层物理概论[M] .武汉：武汉大学出版社，1999.

[3] GOODMAN J M.HF communication：Science and Technology[M] .Van Nostrand，New York，1992.

[4] WANG Jian，FENG Xiaozhe，CHEN Li.Basic MUF observation and comparison of HF radio frequency prediction based on different ionosphere models[C] //9th International Symposium on Antenna，Propagation and EM Theory（ISAPE），2010，403－406.

[5] HF propagation prediction method[R] .ITU－R 533－7，2001.

[6] 中国参考电离层[M] .GJB1925－1994，1994.

[7] ZOLESI B，BELEHAKI A，TSAGOURI I，et al.Real－time updating of the simplified ionosphere regional model for operational applications[J] .Radio Science，2004，139（2），doi：10.1029/2003RS002936.

[8] TSAGOURI I，ZOLESI B，BELEHAKI A，et al.E－valuation of the performance of the real－time updated simplified ionospheric regional model for the European area[J] .Journal of Atmospheric and Solar－Terrestrial Physics，2005，67（12）：1137－1146.

[9] ZOLESI B，CANDER L R，De and FRANCESCHI G.Simplified ionospheric regional model for telecommunication applications[J] .Radio Science，1993，28（4）：603－612.

[10] LOCKWOOD M.A simple M－factor algorithm for improved estimation of the basic maximum usable frequency of radio waves reflected from the ionospheric F region[J] .IEE Proceedings－F：Communication，Radar and Signal Processing，1983，130（4）：296－302.

[11] PIETRELLA M，PERRONE L.Instantaneous space weighted ionospheric regional model for instantaneous mapping of the critical frequency of the F2 layer in the European region[J] .Radio Science，2005，40（1），doi：10.1029/2003RS003008.

[12] 黄德耀.短波电路最高可用频率准实时预报方法[J] .通信学报，1991，12（6）：105－107.HUANG Deyao.Quasi－real－time forecast method of the shortwave circuit MUF[J] .Journal on Communications，1991，12（6）：105－107.（in Chinese）

[13] ZENG Wen，ZHANG XunJie.Prediction of HF communication MUF in the region of south china sea[J] .IEEE Antennas and Propagation Magazine，1999，41（4）：35－38.

[14] CARMI A，GURFIL P，KANEVSKY D.Methods for sparse signal recovery using Kalman filtering with embedded pseudo－measurement norms and quasinorms[J] .IEEE transactions on Signal Processing，58（4）：2405－2409，2010.

[15] MURALI R.Data－based Techniques to Improve State Estimation in Model Predictive Control[D] .University of Wisconsin－Madison，October 2007.

[16] 郑宝玉，等译，Simon Haykin著.自适应滤波器原理（第四版）[M] .北京：电子工业出版社，2006.

[17] KALMAN R E.A new approach to linear filtering and prediction problems[J] .Journal of Basic Engineering，1960，82（1）：35－45.