高阶曲线矢量有限元方法实现及关键问题

尹文禄 杨 虎 肖 科 柴舜连 毛钧杰

（1.西南电子电信技术研究所，四川 成都610041；2.国防科技大学电子科学与工程学院，湖南 长沙410073）

1.引 言

有限元方法由于具有处理不均匀媒质和复杂几何体的能力，在电磁计算领域得到了广泛的研究与应用。如何构造基函数及提高其收敛速度，是有限元发展的一个重要方向。从20世纪80年代末起，各种高阶矢量元由于具有以较少的未知量获得较高精度的优点[1]，成为研究的热点方向之一[2－3]。其中，基于重心坐标的三角形、四面体单元能对任意复杂几何体进行精确、灵活的建模，且在未知量相同的情况下，计算精度远高于其它形式的基函数（如四边形、六面体等）[4]，因此应用最为广泛。针对 Nedelec隐式的构造方法[5]，各种四面体矢量基函数层出不穷，可分为两类：插值基[6]和叠层基[7]，文献[1] 、[8] －[9] 对各种形式的高阶四面体矢量元进行了系统构建、实现与性能比较，验证了满足相同函数空间的插值（或叠层）矢量基函数具有相同计算精度。

有限元法分析电磁问题存在两个近似：一是通过网格剖分对目标模型进行区域离散引起的模型误差，二是通过选取基函数来近似场分布带来的计算误差，问题求解精度取决于这两个近似误差的叠加效果。对于后一个近似，可采用各种高阶插值或叠层矢量基函数来提高场近似的精度；而对于前一个近似，当采用直线单元分析曲线边界时，对几何模型的近似程度决定了求解精度。随着高阶单元剖分尺寸增加，线性规则单元对曲边界不能很好地模拟。为了克服该缺点，各种曲线元被引入到高阶矢量元中，通过协变映射，将曲线单元映射为直线单元进行计算。目前，针对曲线矢量元实现的文献主要集中在四边形和六面体形式[10－12]，分析三角形和四面体的文献较少[13－14]。针对这个问题，在文献[14] 的基础上，进一步完善高阶四面体曲线矢量元的实现过程，并讨论了其实现流程及一些关键问题，最后通过数值实例验证了曲线矢量元极好的计算性能。

2.高阶曲线矢量元的实现公式

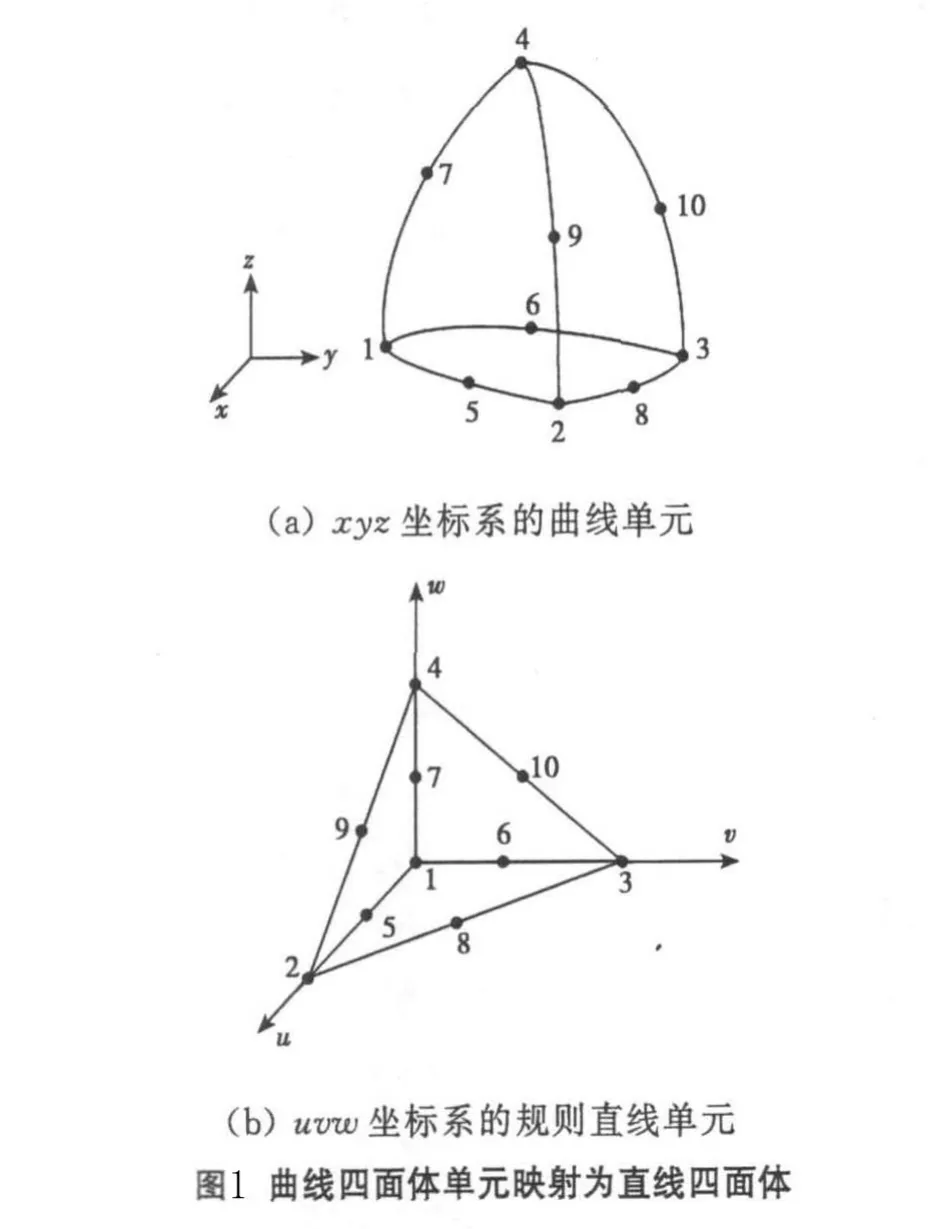
如图1所示，设真实的曲线不规则图形所在的xyz坐标系为全局坐标系，而映射后标准规则图形所在的uvw坐标系为局部坐标系，即原点为（0，0，0）的标准笛卡儿坐标系。

则曲线矢量元的实现过程分为以下几个步骤：

1）研究曲线坐标变换的相关公式，得到局部坐标系下两种类型单元矩阵的显式积分公式。

2）选择合适阶次的曲线映射函数，推导对应的曲线映射Jacobian矩阵。

3）选择合适的矢量基函数，推导该矢量元及对应旋度公式在局部坐标系下的表达形式。

4）选择合适的积分法则，数值求解曲线矢量元的单元矩阵。

5）组合单元矩阵并强加边界条件，得到整体矩阵并求解矩阵方程，对计算的数据后处理。

与直线形式的矢量元相比[1]，步骤①～④是曲线矢量元实现时所独有的。

2.1 三维协变映射

定义逆协变映射为F∶（x，y，z）→（u，v，w），对应的Jacobian矩阵J（F）为

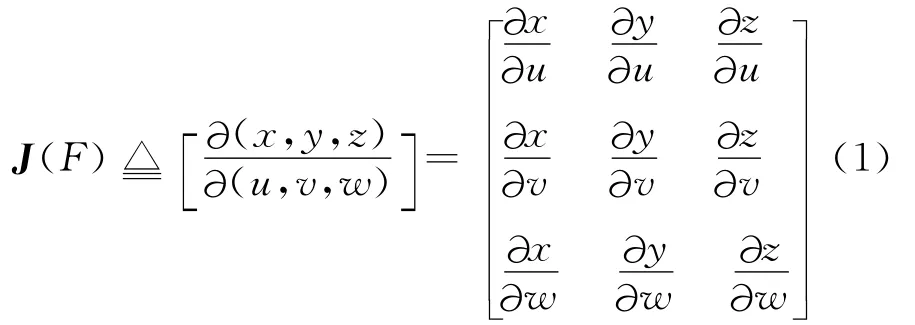
则协变映射为F－1∶（u，v，w）→（x，y，z）。此时，

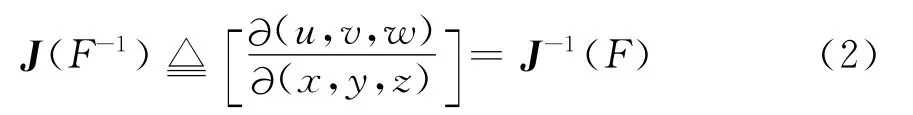
由JJ－1＝I，则det（J－1）＝1/det（J）。显然，在uvw坐标系计算偏导要比在xyz坐标系更容易，因为在该坐标系下曲线映射函数已知，可得到精确解析值；而在xyz坐标系下，网格单元通常是非规则的，对应积分非常繁琐。

设r为xyz坐标系从原点到任意点P（x，y，z）的矢量，由全微分的概念[15]，

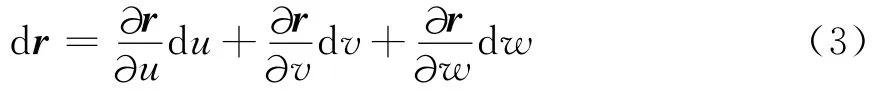
则uvw坐标系单位矢量定义为[16]

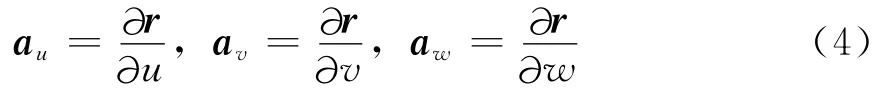
从而，互易单位矢量可定义为[16]

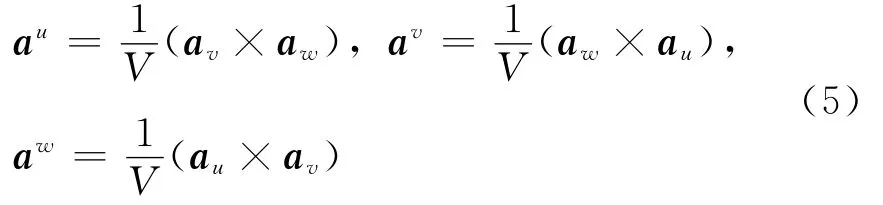
单位矢量和互易单位矢量满足双正交关系aiaj＝δij.

应用曲线坐标投影关系，任意矢量场W可用协变分量或逆协变分量表示[17]：

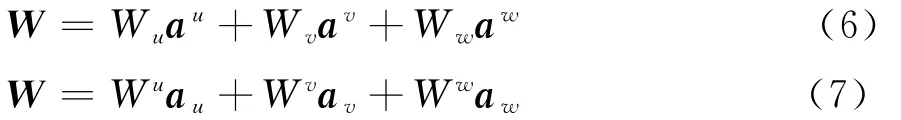
式中：Wu，v，w＝W·au，v，w为协变分量；Wu，v，w＝W·au，v，w为逆协变分量。显然，协变分量表示矢量场W的切向分量，逆协变分量表示W的法向分量。

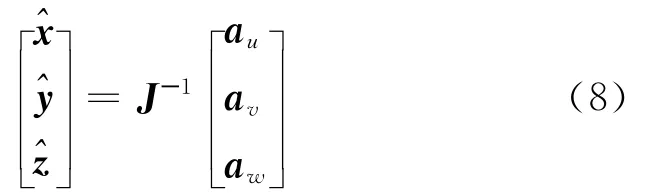
考虑到协变分量的定义，则协变分量之间的映射关系为

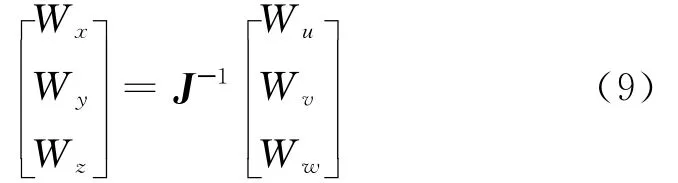
根据偏微分理论[18]，任意函数f的偏导分量之间的映射关系为

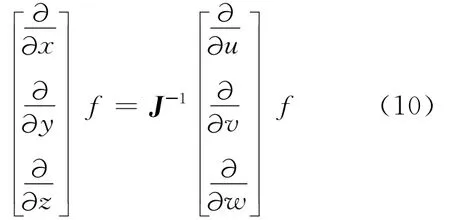
2.2 局部坐标系下曲线单元矩阵积分公式

将两种坐标系中各分量的映射关系式（8）至式（10）代入xyz坐标系下的旋度场可得

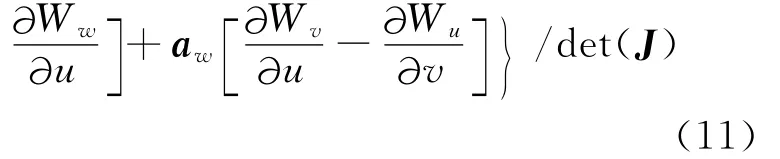
比较逆协变分量公式（7）与式（11），则可定义uvw坐标系下▽×W的逆协变分量

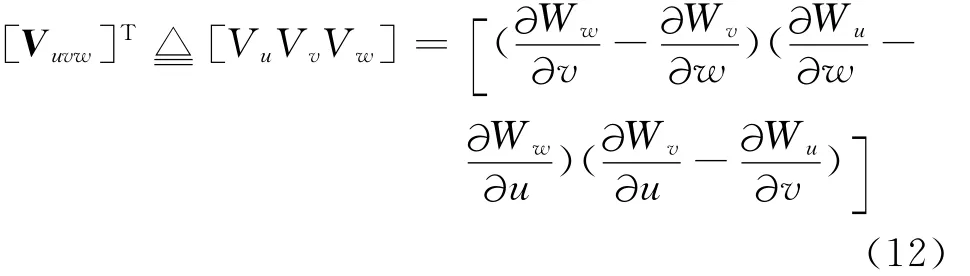
同理，定义xyz坐标系下▽×W的逆协变分量

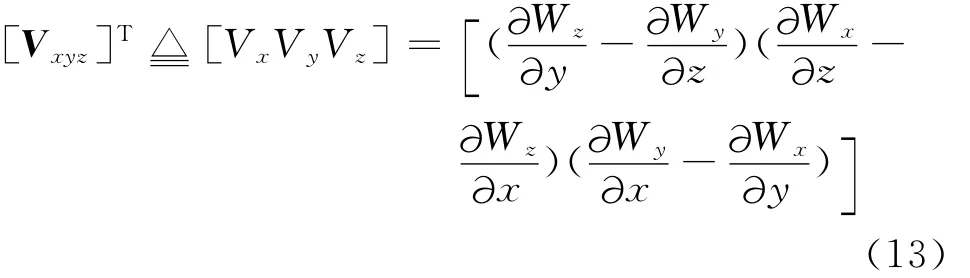
进一步推导可得两者之间存在以下关系

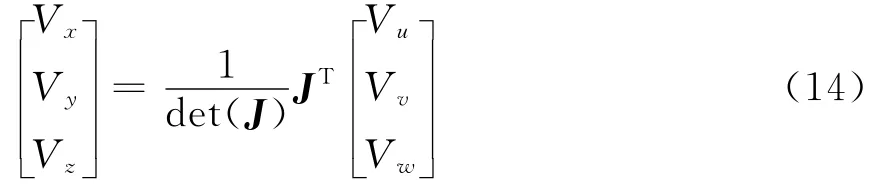
显然，与式（14）相比，文献[17] P119式（42）、文献[14] P441式（14）对应的公式都是不对的，缺少这一项。

据此，矢量有限元方法中单元矩阵所包含的两个积分公式可转换为uvw坐标系下的积分形式。

由三重积分的一般变量替换公式[18]

则单元矩阵

为了公式的简单起见，式（16）将Vuvw缩写为V.

对于早期大部分文献而言，公式推导都是假定单元结点顺序满足右手系关系，此时，det（J）恒为正。为了满足单元交界面处棱边方向的一致性（均从较小点指向较大点），采用文献[1] 提出的结点编码方法，即规定结点中的4个顶点（i1，i2，i3，i4）输出满足结点递增顺序（设i1＜i2＜i3＜i4），显然这将不满足右手系关系，因此J的行列式要加绝对值。

2.3 曲线映射函数选取及Jacobian矩阵确定

为了将xyz坐标系中的曲线单元映射为uvw坐标系下的规则直线单元，必须要定义相互之间的曲线映射法则。采用二阶Lagrangian多项式函数作为曲线映射函数，实现对曲边界的二阶近似。

对于n阶四面体结点单元，曲线映射函数定义为[4]

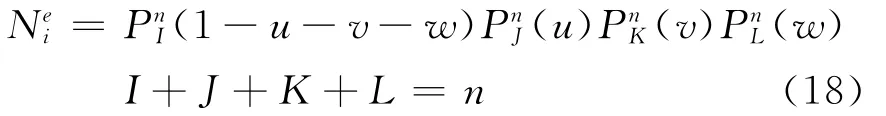
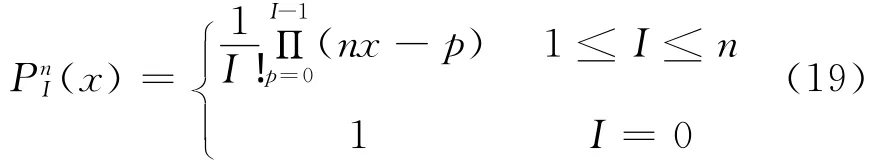
因此，二阶曲线映射函数的具体表达式如下[4]

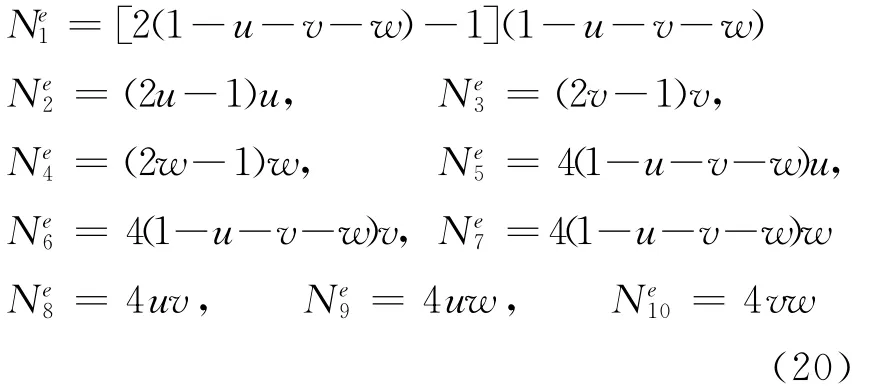
为了获得正确的曲线映射关系，要使单元结点输出格式满足正确的对应关系，如图1所示。

则xyz坐标系下的任意结点坐标采用uvw坐标系可表示为

式中 （xi，yi，zi）为xyz坐标系下的结点坐标。根据Jacobian矩阵定义式（1），则

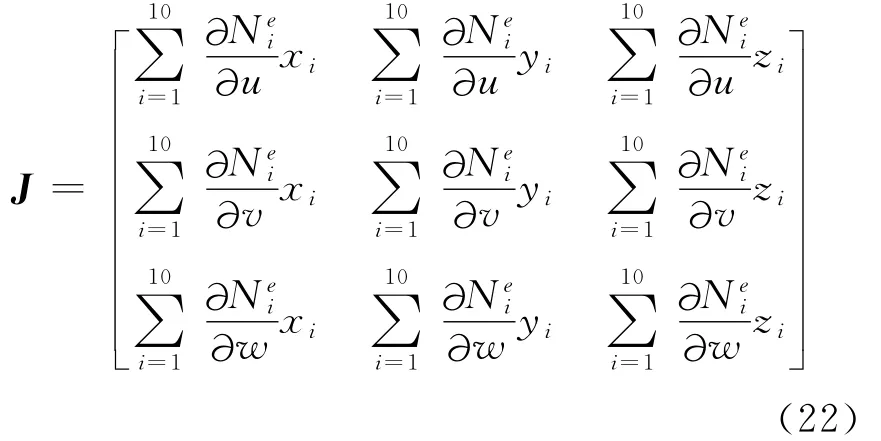
因此，只要计算出曲线映射函数对u、v、w的偏导数，则J矩阵就很容易计算得到。求出J后，由于J矩阵仅为3×3阶，因此可采用直接方法求解单元矩阵计算时所需的J－1、J－1T、det（J）。由于J矩阵与数值积分点的位置相关，因此在计算单元矩阵时必须在每一个积分点处都要进行计算。

2.4 矢量基函数及相关旋度的局部坐标表示

由文献[1] [9] ，只要满足相同的Nedelec函数空间，则基函数可获得相同的计算精度。因此，选取二阶非归一化Webb99叠层基[7]作为单元内场近似基函数。则第i条棱边上的边元基函数可表示为

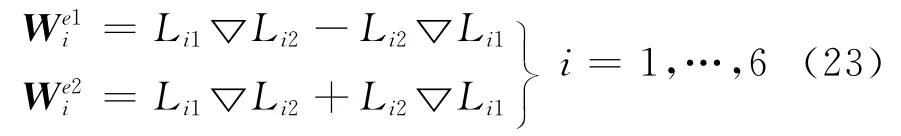
第i个面元基函数可表示为

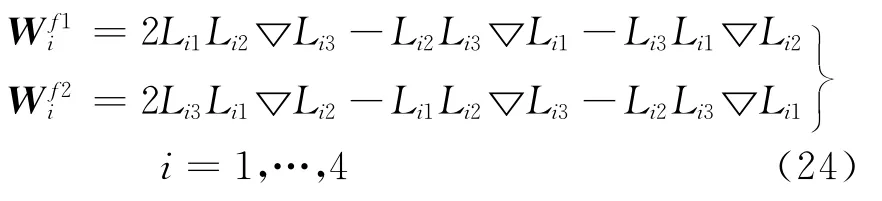
式中：Li为重心坐标。显然，采用基函数分类技术，二阶矢量基函数可分为四类：e1、e2、f1、f2。为了保证四面体单元之间切向场连续，采用文献[1] [19] 定义的二阶四面体矢量元的四类分量取法，即在每个面内（i1，i2，i3）（i1＜i2＜i3），棱边e1方向从较小点指向较大点，e2方向与之相反，f1在棱边i1－i2上，取点顺序为（i1，i2，i3）；f2在棱边i1－i3上，取点顺序为（i3，i1，i2）。

如图1所示，规则四面体棱边长度为1时，u、v、w分别表示重心坐标Li2、Li3、Li4，即

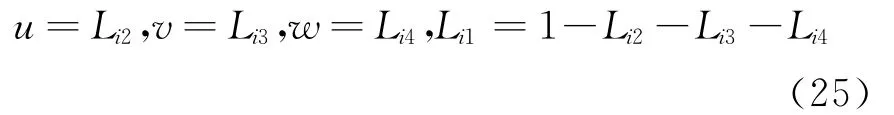
由梯度在曲线坐标系中的定义[16]，

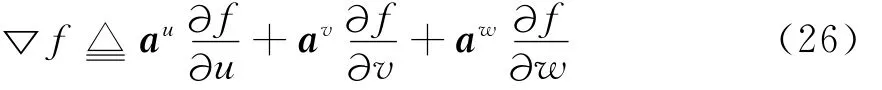
则式（5）定义的互易单位矢量可改写为

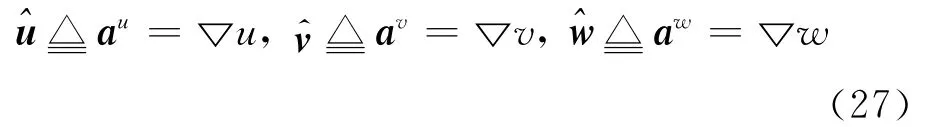
以e1的第一个分量（即对应棱边为i1－i2）为例，代入式（25）、式（27）可得

从式（28）可以看出，基函数的协变分量[Wu Wv Ww]1＝[1－v－wuu] 。由式（12），基函数旋度的逆协变分量 [Vu Vv Vw]1＝ [0－2 2] 。

采用相同的方法，对Webb99叠层基的其它基函数进行局部坐标表示，可得到基函数的协变分量、基函数旋度的逆协变分量（详细结果可参考文献[20] ，在此不再赘述）。需要指出的是，与文献[14] 推导结果不同的原因在于，文中采用的基函数对面元形式进行了归一化，同时f1、f2面元分量分别按（i1，i2，i3）、（i3，i1，i2）结点顺序进行选取，从而确保了面元选择的唯一性，便于程序实现与单元矩阵组合。

3.高阶曲线矢量元实现流程及关键问题

图2给出了采用固定阶曲线矢量元的程序实现流程。具体实现时，先通过合适的判别准则，得到曲线单元编号的数组；然后在计算单元矩阵时分别采用合适的积分公式进行处理。当单元为曲线单元时，采用高斯数值积分进行计算；当单元为直线单元时，则采用高斯解析公式进行计算。与直线型矢量元的实现过程相比[20]，除了要增加图2中虚线框所示的内容外，其它工作完全相同。

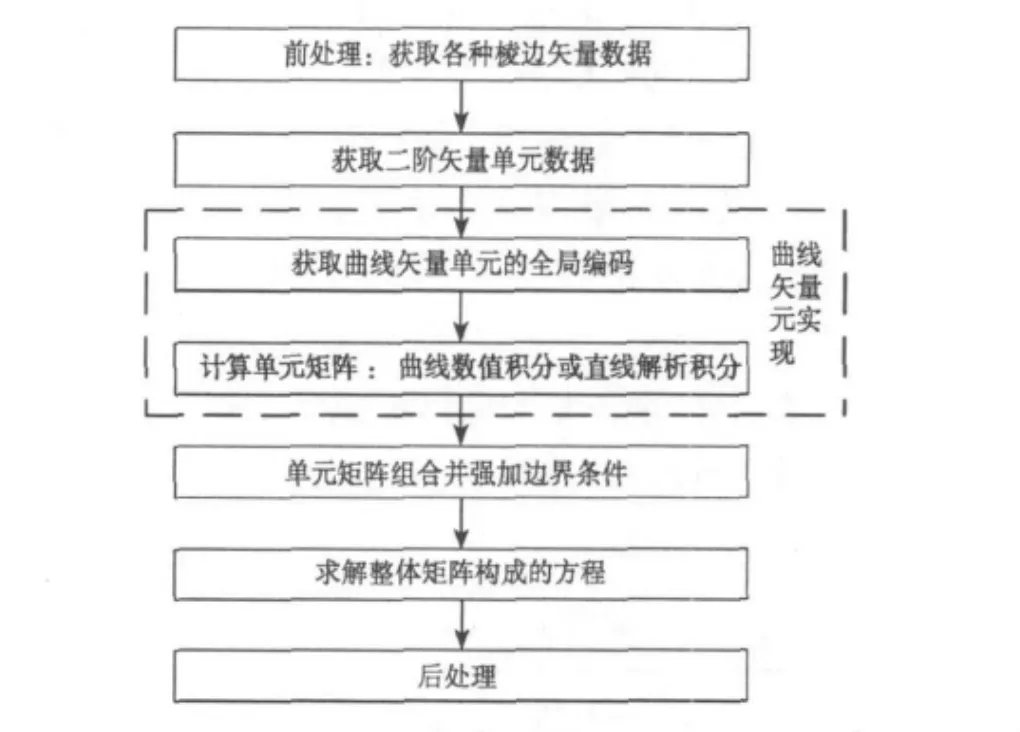
图2 二阶四面体曲线矢量元的实现流程

在混合阶矢量元的实现过程中，需要解决以下几个关键问题：

3.1 曲线矢量单元的判别

选择合适的判别准则，对每个剖分单元进行判断，若满足曲线单元条件（单元至少含有一条曲线即可），则取为曲线单元，否则为直线单元。

这是因为，采用高阶数值积分法则进行曲线单元积分时，极大增加了计算量。因此，为了降低计算成本，只在含曲边的区域（如曲线边界、不同媒质之间的曲交界面处等）上采用曲线单元，而在其它位置采用直线单元。由于曲线矢量元满足了相邻单元切向场分量连续（该条件即使在曲边上也是满足的），因此在不同单元形式的交界面处进行正常组合即可得到整体矩阵。

3.2 曲线单元矩阵的数值积分实现

在计算单元矩阵时，对每一个单元编号，先判断属于曲线元还是直线元，直线单元采用二阶矢量元高斯解析积分公式[8]进行计算。对于曲线单元而言，由于曲线映射函数Ni、基函数Wi都是u、v、w的函数，这导致了单元矩阵中的待积分系数（如J、J－1、V、W 等）都是函数矩阵，使得很难求出积分的解析表达式，从而只能通过数值积分来求解曲线单元矩阵。在有限元法中，由于被积函数复杂，一般采用高斯数值积分，即可用较少的积分点达到较高的计算精度，从而节省计算时间。

基于四面体单元的三维高斯数值积分公式为[4]

式中：F（L1i，L2i，L3i，L4i）表示被积函数；（L1i，L2i，L3i，L4i）表示积分点；Wi为加权因子；ns为积分点数；V为积分单元的体积。该积分公式一个重要性质在于[21]，如果被积函数多项式的阶数≤（1，2，3，4，5），那么，选择ns＝（1，4，5，11，14）则可精确求出积分。

具体而言，曲线单元矩阵高斯数值积分的实现流程如图3所示。

图3 曲线单元矩阵高斯数值积分的实现流程

当采用局部坐标分量表示单元矩阵积分点时，则

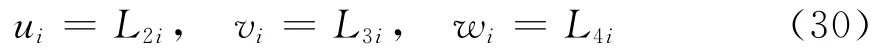
显然，积分点与L1i无关，因为L1i＝1－u－vw.当规则直四面体的棱边长度为1时，高斯积分对应体积V＝1/6。

本文研究表明，高斯积分点的数目与曲线映射函数的阶次无关，仅与基函数阶次有关。当采用n阶矢量基函数时，可获得2n阶计算精度，则对应高斯积分只要满足2n阶精度即可。如棱边元可获得2阶计算精度，因此采用2阶4点Gellert积分[21]即可获得精确结果；而二阶矢量元可获得4阶精度，因此采用4阶11点Gellert积分即可。当然，采用更高阶高斯积分同样可获得相同的计算精度，但无疑增加了计算代价。如采用6阶24点或8阶45点Keast积分[22]也可获得与4阶11点Gellert积分相同精度。需要指出的是，所有Keast积分与体积无关，因此被积函数不需乘以体积1/6；同时，8阶45点Keast积分的首个积分点权值应为－0.039327（即加一个负号），文献[23] 纠正了该错误。

4.数值结果

以下给出几个算例的计算结果，分别从计算精度、矩阵条件数等角度验证曲线矢量元较之直线单元具有更好的计算性能。其中，直线单元分别采用一阶非归一化棱边元、二阶非归一化Webb99叠层基；曲线单元在采用二阶曲线映射函数的基础上，基函数分别采用一阶非归一化棱边元、二阶非归一化Webb99叠层基。

4.1 验证结果

采用与文献[1] 相同的数值实验方法分析r＝1 m空气填充球腔的谐振本征值。在不同网格尺寸h的情况下，计算前八个非零本征值与解析解之间的归一化均方误差ε.以整体矩阵T为例，计算不同矢量元对应的矩阵条件数。其中，含边界棱边的单元采用曲线元，其余单元采用直线元。

图4绘出了归一化均方误差ε与网格尺寸h之间的关系。可以看出，分析曲线模型的精度主要受限于对模型曲边界的近似精度。在相同尺寸的前提下，若采用直线元分析曲线区域，高阶元只能达到低阶元的精度；若采用曲线元分析曲线区域，二阶元的计算精度远高于棱边元。值得一提的是，曲线二阶矢量元的收敛速度为O（h－2.07），而直线二阶矢量元分析直线模型时可达到 O（h－4）[1]。这是因为，二阶曲线映射函数虽比直线元更能提高近似曲线边界的精度，但不能准确模拟球边界，必须要提高曲线映射函数的阶次或采用Bezier四面体[24]等特殊曲线映射单元。

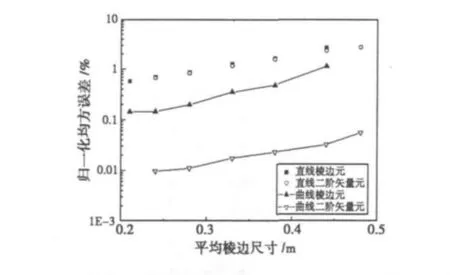
图4 球腔相对误差与平均棱边尺寸的关系

图5绘出了归一化均方误差ε与未知量数目之间的关系。可以看出，当分析曲线目标时，在相同未知量数目的前提下，采用高阶曲线矢量元精度远优于采用直线形式的高、低阶元或曲线单元形式的低阶元；而高阶直线元虽然在网格尺寸相同的情况下获得与低阶直线元相比拟的计算精度，但未知量数目急剧增加。这充分验证了，只能先采用曲线元对曲线模型进行高精度建模，高阶矢量基函数才能发挥以较少未知量获得较高精度的优点。

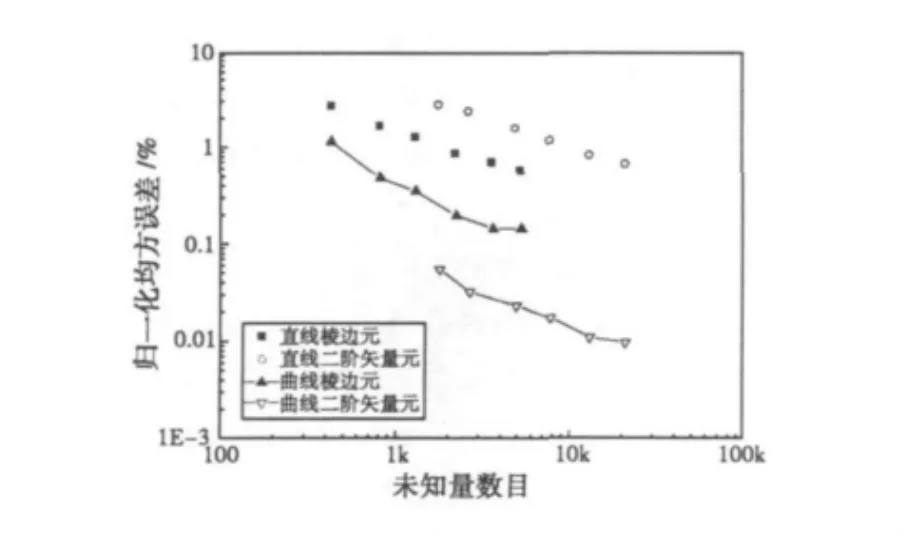
图5 球腔相对误差与未知量数目的关系

图6给出了在不同未知量数目情况下，采用直线、曲线矢量单元得到的整体矩阵T条件数。可以看出，不论采用曲线元还是直线元形式，只要基函数相同，则矩阵条件数几乎完全相同 （图中相同类型基函数的条件数曲线完全重合）。这意味着，在极大提高了计算精度的同时，曲线元形式并不影响计算效率。

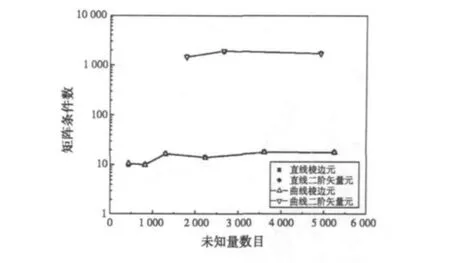
图6 矩阵条件数与未知量数目的关系

4.2 具体应用

为了进一步说明曲线矢量元在提高计算精度的能力，采用曲线矢量元分析图7所示的圆柱腔，在曲边界、内部填充媒质的曲交界面处采用曲线元，其余部分采用直线元。

如图8所示，采用各种直线、曲线形式的基函数对该腔体进行分析，得到不同未知量数目情况下的主模谐振频率的计算结果。其中，测量结果为6.943 GHz[25].

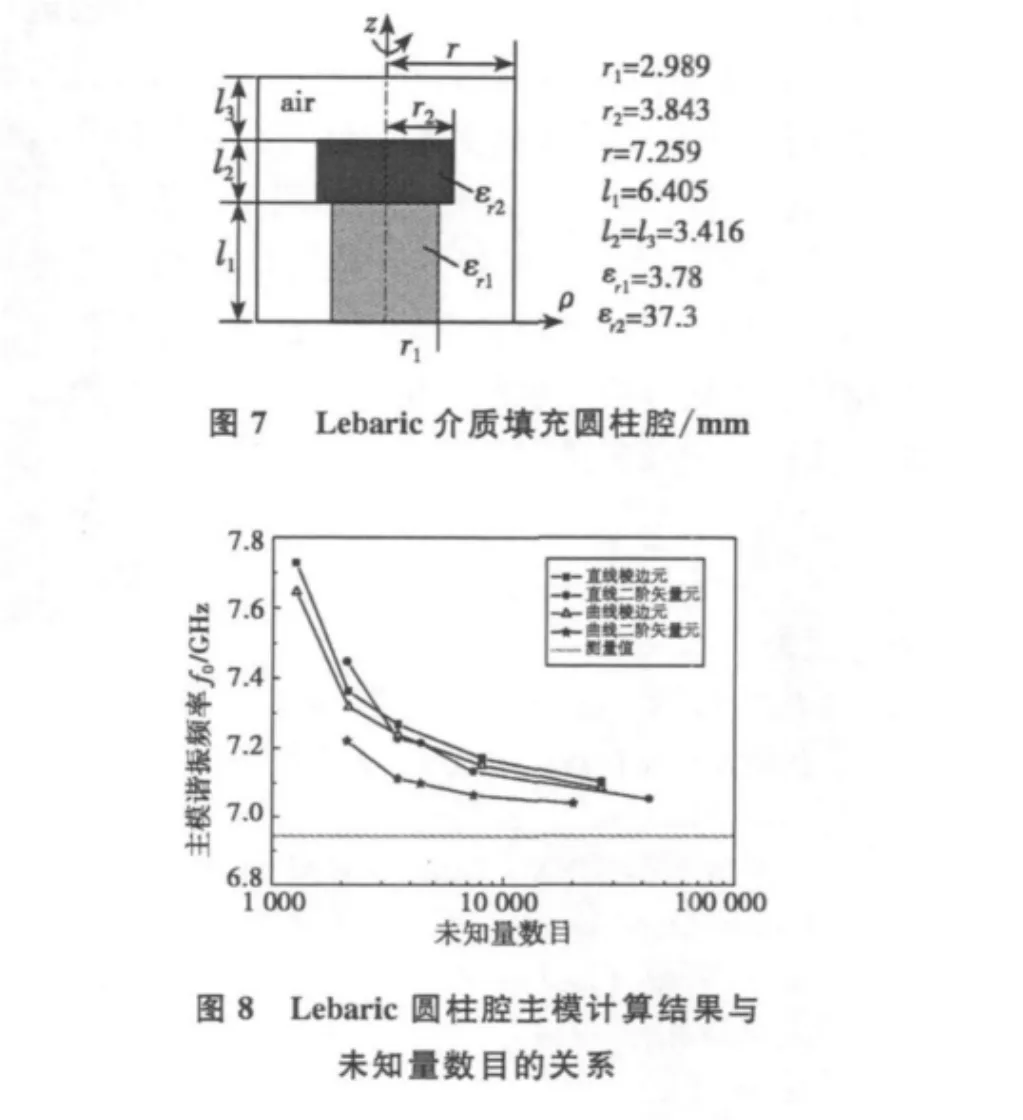
图9绘出了对Lebaric介质填充圆柱腔计算的主模谐振频率归一化均方误差ε与未知量数目之间的关系。可以看出，高阶曲线矢量元由于同时具有对曲边界模拟程度好、对场近似程度高的特点，因此获得了比其它形式矢量元更高的计算精度。

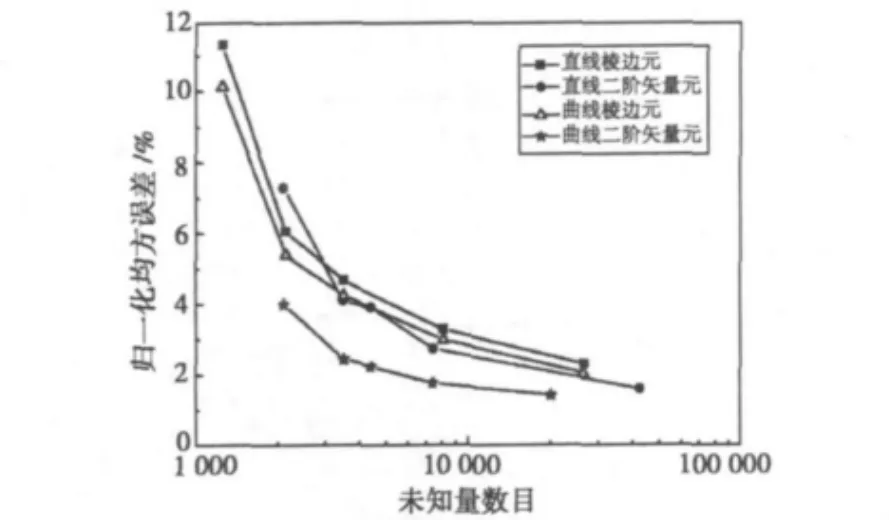
图9 Lebaric圆柱腔主模相对误差与未知量数目的关系

5.结 论

系统研究了曲线矢量元的实现过程，详细分析了实现过程中的关键问题及相关细节。具体而言，以二阶曲线映射函数结合二阶非归一化Webb99叠层基为例，系统而显式地研究了曲线矢量元的实现流程和关键问题 （如协变映射的概念、曲线单元矩阵的公式推导、曲线映射函数选取与Jacobian矩阵求解、矢量基函数及其旋度在局部坐标系中的展开、曲线单元矩阵的高斯数值积分技术等）。然后，通过分析r＝1 m球腔谐振本征值问题，从计算精度、条件数等方面对各种直线或曲线形式的高、低阶矢量元进行比较，得到了一些有益的结论。最后，将其用于分析复杂腔体问题，获得了极好的计算结果。上述分析方法和结论可直接推广到任意形式、更高阶曲线矢量元的研究与应用。

[1] 尹文禄，邓 聪，柴舜连，等.基于Nedelec条件的高阶矢量元构造与实现 [J] .微波学报，2009，25（3）：7－12.YIN Wenlu，DENG Cong，CHAI Shunlian，et al.Construction and implementation of higher order vector elements based on Nedelec constraints [J] .Journal of Microwaves，2009，25 （3）：7－12.（in Chinese）

[2] NOTAROS B M.Higher order frequency－domain computational electromagnetics [J] .IEEE Transactions on Antennas and Propagation，2008，56 （8）：2251－2276.

[3] 尹文禄，叶良丰，邓 聪，等.基于高阶四面体矢量元的大规模本征值求解 [J] .微波学报，2010，26（1）：12－18.YIN Wenlu，YE Liangfeng，DENG Cong，et al.Efficient solution of large－scale eigenvalue problems based on higher order tetrahedral vector elements[J] .Journal of Microwaves，2010，26 （1）：12－18.（in Chinese）

[4] JIN J M.The Finite Element Method in Electromagnetics[M] .2nd ed.New York：John Wiley and Sons，2002.

[5] NEDELEC J C.Mixed finite elements in R3[J] .Numerische Mathematik，1980，35 （9）：315－341.

[6] GRAGLIA R D，WILTON D R，PETERSON A F.Higher order interpolatory vector bases for computational electromagnetics [J] .IEEE Transactions on Antennas and Propagation，1997，45 （3）：329－342.

[7] WEBB J P.Hierarchal vector basis functions of arbitrary order for triangular and tetrahedral finite elements [J] .IEEE Transactions on Antennas and Propagation，1999，47 （8）：1244－1253.

[8] 尹文禄，邓 聪，杨 虎，等.高阶四面体矢量元的实现与性能比较 [J] .微波学报，2010，26 （3）：15－20.YIN Wenlu，DENG Cong，YANG Hu，et al.Implementation and performance comparison for higher order tetrahedral vector elements [J] .Journal of Microwaves，2010，26 （3）：15－20.（in Chinese）

[9] YIN W L，DONG J，CHEN L，et al.Systematic construction and performance comparison for higher order hierarchical tetrahedral vector elements[C] //International Conference on Wireless Communications and Signal Processing.Suzhou China，2010：1－4.

[10] CROWLEY C W，SILVESTER P P，HURWITZ H.Covariant projection elements for 3D vector field problems[J] .IEEE Transactions on Magnetics，1988，24 （1）：397－400.

[11] WANG J S，IDA N.Curvilinear and higher order＇edge＇finite elements in electromagnetic field computation [J] .IEEE Transactions on Magnetics，1993，29 （2）：1491－1494.

[12] PALMA M S，SARKER T K，CASTILLO L E G，et al.Iterative and Self Adaptive Finite Elements in Electromagnetic Modelling [M] .Boston：Artech House，1998.

[13] MARAIS N，DAVIDSON D B.Numerical evaluation of hierarchical vector finite elements on curvilinear domains in 2－D [J] .IEEE Transactions on Antennas and Propagation，2006，54 （2）：734－738.

[14] SWARTZ J P，DAVIDSON D B.Curvilinear vector finite elements using a set of hierarchical basis functions [J] .IEEE Transactions on Antennas and Propagation，2007，55 （2）：440－446.

[15] SILVESTER P P，FERRARI R L.Finite Elements for Electrical Engineers [M] .3rd ed.Cambridge：Cambridge University Press，1996.

[16] STRATTON J A.Electromagnetic Theory [M] .New York：McGraw－Hill，1941.

[17] ITOH T，PELOSI G，SILVESTER P P.Finite Element Software for Microwave Engineering [M] .New York：John Wiley ＆Sons，1996.

[18] 汪 浩.高等数学 （下册）[M] .长沙：国防科技大学出版社，1988.

[19] 尹文禄，邓 聪，赵 菲，等.高阶矢量有限元方法实现及关键问题 [J] .电波科学学报，2009，24（2）：349－353.YIN Wenlu，DENG Cong，ZHAO Fei，et al.Implementation for higher order vector FEM and some key issues [J] .Chinese Journal of Radio Science，2009，24 （2）：349－353.（in Chinese）

[20] 尹文禄.高阶矢量有限元方法在电磁领域中的研究及应用 [D] .长沙：国防科技大学，2010.YIN Wenlu.Study and Application on Higher Order Vector FEM in Electromagnetic Field [D] .Changsha，P.R.China：National University of Defense Technology，2010.

[21] GELLERT M，HARBORD R.Moderate degree cubature formulas for 3－D tetrahedral finite－element approximations [J] .Communications in Applied Numerical Methods.1991，7 （6）：487－495.

[22] KEAST P.Moderate－degree tetrahedral quadrature formulas [J] .Computer Methods in Applied Mechanics and Engineering，1986，55 （3）：339－348.

[23] SAVAGE J S，PETERSON A F.Quadrature rules for numerical integration over triangles and tetrahedra[J] .IEEE Antennas and Propagation Magazine，1996，38 （3）：100－102.

[24] MARTINI E，SELLERI S.Innovative class of curvilinear tetrahedral elements [J] .IEE Electronics Letters，2001，37 （9）：557－558.

[25] LEBARIC J E，KAJFEZ D.Analysis of dielectric resonator cavities using the finite integration technique [J] .IEEE Transactions on Microwave Theory and Techniques，1989，37 （11）：1740－1748.