海浪对水下甚低频最小频移键控信号解调的影响

陆 洪 潘威炎

（中国电波传播研究所，山东 青岛266107）

1.引 言

按照ITU的规定，甚低频（VLF）是指3～30 k Hz的频率范围，它对应的自由空间波长为10～100 km.由于地面与电离层对于VLF波都有良好的反射特性，以及地面与电离层之间的距离与VLF波长可比拟，VLF波在地面与电离层之间被来回反射导引地传播，一般称这种传播方式为地—电离层波导传播。对于VLF波而言，地面与电离层可理解为良好的反射壁，VLF波在其中传播损耗很小，一般每千千米的衰减率约为1～3 dB；VLF电波亦能渗透一定深度的海水，它在海水中的衰减率约为4～6 dB/m，利用VLF信号进行通信是世界各国海军用作对潜通信指挥的主要技术手段。VLF电波从发射台到水下潜艇的接收天线之间的传播路径很长，涉及的介质包括地面及浅层的土壤、大气层、电离层以及海水。电波经长距离传播后，不可避免地产生失真和畸变，从而使它携带的信息在解调时产生误码。当潜艇在水下接收VLF信号时，由于海浪起伏，使水下接收的VLF信号的幅度与相位随海浪起伏产生相应的周期性变化，一般VLF通信在水下的可接收深度为水下十多米，VLF波在海水中的波长也只有十多米，而海浪的起伏一般可达几米，因此，水下的VLF信号无论从幅度与相位的角度上，其变化都是显著的[1]。由文献[2] [3] 可知，在水下接收点平均深度和电波频率不变的情况下，海浪波动对水下接收点电磁场的影响取决于海浪的波高。

在已知海水的水文状况（海水导电率）等条件下，建立海水中VLF传播信道模型，针对VLF通信系统中常用的MSK调制信号，用计算机仿真方法计算各种海浪等级及信噪比条件下，水下MSK信号差分解调的误码率，分析通信误码率与海浪浪高、信噪比等参数的关系。

2.海水中VLF传播信道模拟

对水下的接收系统，一般采用交叉磁棒天线接收水平磁场，或采用拖曳电极天线接收水平电场。按照VLF电波传播规律，水下的水平电磁场可表示为

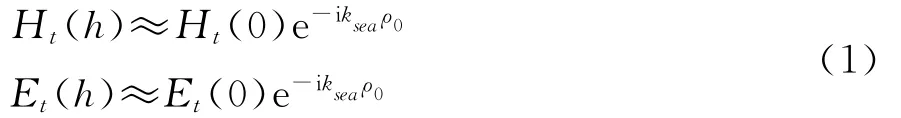
式中：Ht（h）、Et（h）分别表示水下离海面深度为h的接收点的水平磁场与电场；Ht（0）和Et（0）分别表示海面上的水平磁场和电场。式中：ksea表示海水中VLF波的传播波数，其表达式为

ρ0是从海面到水下接收点的最短传播距离，它的大小随着海浪的起伏而变化。海浪波形及水下接收点示意如图1。

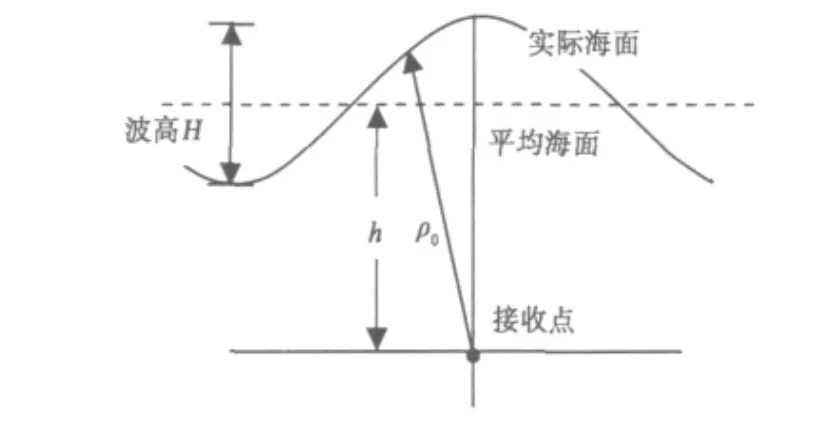
图1 海浪波形示意图

相邻波峰与波谷的垂直距离为波高H，水下接收点至海面的最短传播距离ρ0可表示为

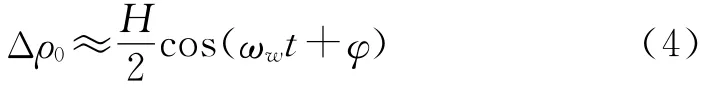
式中：ωw为海浪变化的角频率；φ为初始相位，它是（0，2π）内均匀分布的随机变量，海浪的周期范围为0.5～20 s.海浪的波高与周期有一定的对应关系，不同海域其关系不同，以我国南洞庭湖为例，其海浪的平均波高与平均周期之间的对应关系为[4]

从严格意义上讲，水面上电磁场的幅度与相位是变化的，从时间域上，由于电离层的随机变化，会使得海面上各处的电磁场亦产生相应的变化。但电离层的随机变化相对于海浪的周期而言，是缓变的，在分析海浪对水下接收信号的影响时，我们可以认为这种变化可以不予考虑。另一方面，水面上相邻各点，电磁场亦是有变化的，但由于VLF波在空气中的波长有10 km以上，所以，在几个海面海浪波长范围内，它的幅度与相位亦可看作是常数。水下接收到的单频电场信号可表示为

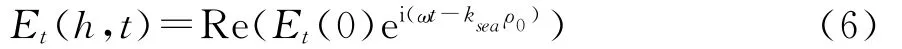
水平磁场也有类似的表达式。由式（6）可将电场水平分量表示为

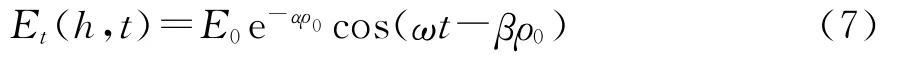
式中：E0为海面上电场的振幅，α、β与ksea间的关系如式（2）。海水中的传播波数ksea对于不同频率的电波，它的实部与虚部都是变化的，从严格意义上讲，海水是一种频率色散介质。当VLF信号用于通信时，它不可避免地需要调制，因此，它不是严格的单色波，在海水中传播，信号波形会因为色散而产生畸变。但在实际应用中，由于VLF通信系统的发射天线带宽的限制，VLF通信信号的带宽一般在100～200 Hz之间，常用的VLF通信信号的载频大约在20 k Hz以上，相对带宽小于1%，故VLF信号是一种窄带信号，加之潜艇在水下接收深度不大，考虑海浪对信号解调的影响时，忽略海水中由频率色散引起的信号畸变影响。

3.水下接收的MSK信号

MSK信号的表达式为[5]

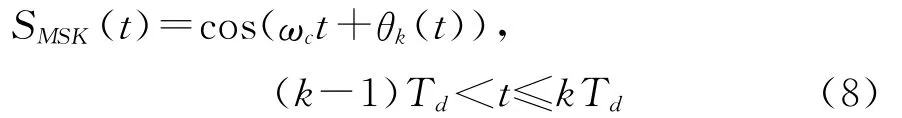
式中

ωc＝2πfc为载波角频率；ak＝±1，分别表示二进制信息1和0；Td为码元宽度；fd＝1/Td为码元速率；φk为第k个码元的初始相位，它在一个码元宽度内是不变的。θk（t）为第k个码元的附加相位。由于MSK信号是相位连续的，前一码元末尾的总相位等于后一码元开始时的总相位，即θk－1（k Td）＝θk（k Td），于是有

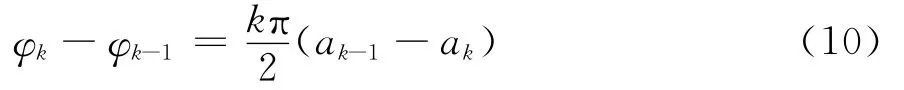
由式（8）可以看出，当ak＝－1时，码元频率ω0＝ωc－π/2Td；当ak＝＋1时，码元频率ω1＝ωc＋π/2Td即在一个码元宽度内MSK信号是一个余弦信号。

由第2节的讨论可知，MSK信号经海水传播后，水下ρ0处接收的信号s（t）可表示为

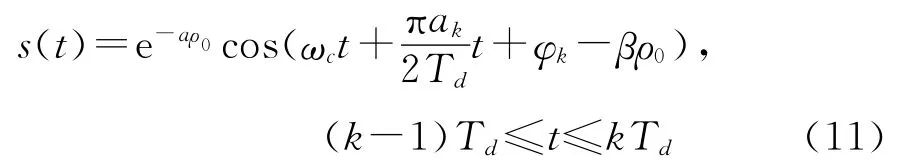
式中：α和β分别为载波对应的衰减常数和相移常数。由于大气噪声、接收设备与天线热噪声的存在，水下接收机接收的电磁信号还应包含噪声，送入解调器的信号为

式中：n（t）是中心频率为ωc的带限高斯白噪声，其均值为0，方差（功率）为，表达式为

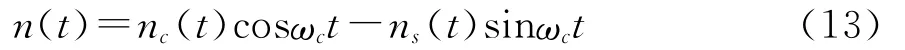
nc（t）、ns（t）与n（t）具有同样的均值和方差。

4.仿真模型

采用差分方法对接收的MSK信号进行解调。系统仿真框图如图2所示。

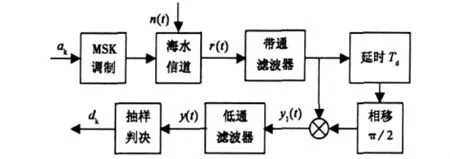
图2 系统仿真模型

MSK调制信号经海水信道后送入接收端。首先对接收信号进行带通滤波，滤除带外噪声；然后将滤波后的信号延时一个码元时间Td并相移π/2后与自身相乘；最后对相乘后的信号y1（t）低通滤波滤除高频分量得到y（t），对y（t）进行抽样判决输出解调码元dk，通过比较ak与dk来确定其是否为误码。

由于ρ0的变化相对于信号来说是非常缓慢的，可以认为在2个码元宽度内无变化，由式（11）、（12），在无噪声时

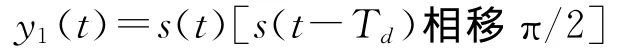
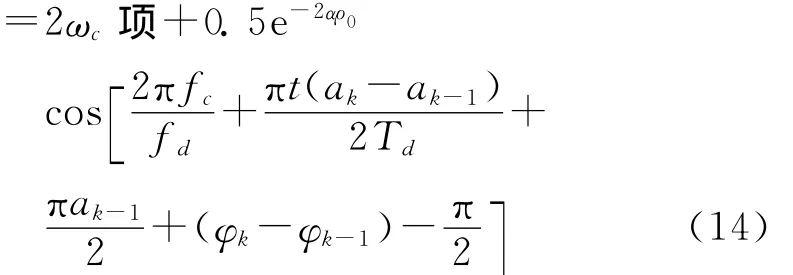
将y1（t）滤除2ωc项，并使载波频率fc为码元速率fd的整数倍，并考虑式（10），可得

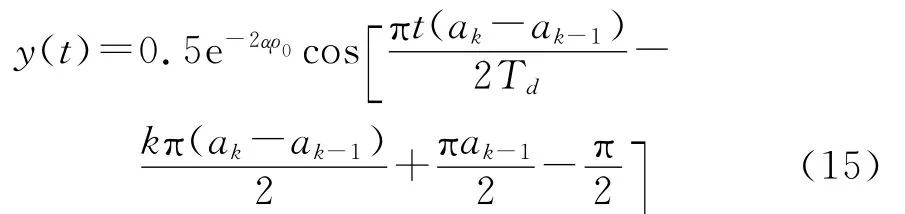
对y（t）在t＝k Td处进行抽样可得

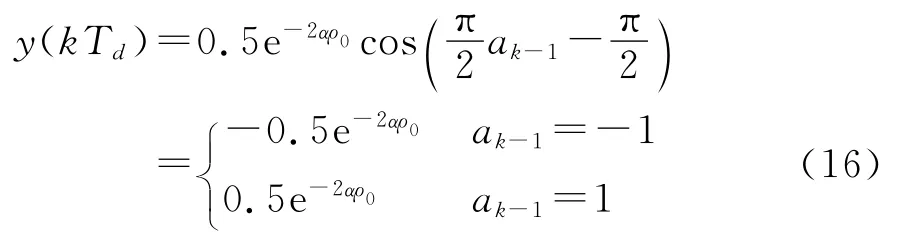
判决准则为

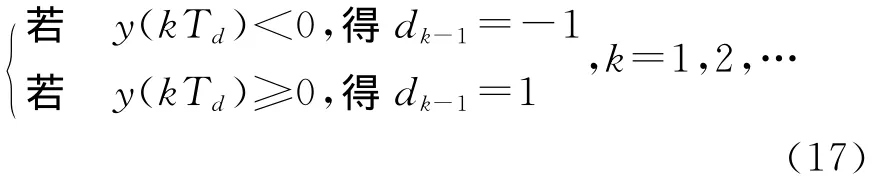
通过比较ak－1与dk－1来确定其是否为误码。仿真中用蒙特卡洛方法对系统的误码性能进行分析。在仿真中每200个码元一组进行调制、传输和解调，并判断是否为误码，更新总误码个数和总码元个数，再对下一组200个码元进行调制、传输和解调。当总误码个数达到70个或总码元数达到106个，则停止运算，计算出对应信噪比下的误码率。

5.仿真结果及分析

用第4节所述方法对不同波高情况下的误码率进行了仿真计算。仿真中假定海浪波高与周期满足式（5）关系。所取波高分别为0.05 m（微波）、1 m（轻浪）、2 m（中浪）、3 m（大浪）、4.5 m（巨浪）和6 m（巨浪）。计算中所取参数为载频fc＝10 k Hz，码元速率fd＝100 bps，采样频率fs＝50 k Hz，海水导电率σ＝4 S/m，接收点深度10 m.仿真结果如图3示。

图3 误码率随信噪比的变化曲线

由图3可以看出当波高为0.05 m（海面平静）时信噪比为8.5 dB即可达到10－4误码率；若要达到相同的误码率，波高为3 m、4.5 m和6 m时信噪比需要分别提高到13.4 dB、17.5 dB和22.3 dB.

由上述结果可以看出：浪高一定时，误码率随着信噪比的增加而下降；相同的信噪比条件下，浪高越小误码率越低。

6.结 论

本文建立了海浪影响下的VLF传播信道模型，通过仿真计算分析了各种海浪等级及信噪比条件下，水下MSK信号差分解调的误码率，得到了海浪影响下的信噪比—误码率曲线。通过对这些曲线的分析，得出了海浪对水下甚低频MSK通信解码影响的一些有用结论，可为水下甚低频MSK通信提供一定参考。另一方面，海浪的变化是极其复杂的，除了浪高与周期外，还有波长、波速等其它要素，文中把海浪简化为具有一定振幅和运动周期的余弦曲线，与真实的海浪波形有一定差异，在实际应用中应综合考虑各种因素。

[1] 潘威炎.长波超长波极长波传播[M] .电子科技大学出版社，2004.

[2] 王永斌，陈卫东，杜 义.海浪对水下电磁场幅值影响的分析[J] .热带海洋通讯，2005，24（1）：38－40.WANG Yongbin，CHEN Weidong，DU Yi.Effect of ocean wave on magnitude of underwater electromagnetic field[J] .Journal of Tropical OceanoGraphy.2005，24（1）：38－40.（in Chinese）

[3] 虢应华，王永斌.海浪对水下电磁场相移统计特性影响分析[J] .无线电工程，2008，38（2）：44－45.GUO Yinghua，WANG Yongbin.Analysis of effect of sea wave on underwater electromagnectic wave phaseshift statistical characteristics[J] .Radio Enfineering，2008，38（2）：44－45.（in Chinese）

[4] 赵利平，连石水，沈 浩，等.南洞庭湖风浪波高和周期的分布[J] .长沙理工大学学报（自然科学版），2005 2（3）：16－21.ZHAO Liping，LIAN Shishui，SHEN Hao，et al.Distribution of height and period of wind waves in south dongting lake[J] .Journal of Changsha University of Science and Technology（Natural Science）.2005，2（3）：16－21.（in Chinese）

[5] 张 辉，曹丽娜.现代通信原理与技术[M] .西安电子科技大学出版社，2002.