有限元＼边界元混合算法分析波导裂缝阵列天线

孙 良 刘其中 邹艳林

（西安电子科技大学天线与微波技术国防科技重点实验室，陕西 西安710071）

1.引 言

波导裂缝阵列天线具有辐射效率高，口面分布易于控制，结构紧凑等许多优点，是雷达和通讯领域最常用的天线之一。国内外许多学者对波导裂缝阵列天线做了大量研究。Khac在七十年代初首先采用矩量法对单个纵缝进行了分析计算[1]，由于他选用分域基点选配方法，计算比较冗繁。之后Lyon和Sangster采用全域基伽略金法对单缝进行了计算[2]。在文献[3] 中，Elliott把缝阵的设计归结为两个基本的方程，通过迭代可以完成对小型缝阵的设计，但这种方法无法考虑波导内部裂缝之间的互耦及波导壁厚的影响，而这些因素对天线的性能有着较大的影响。Hamadallah[4]，Gulick 和 Elliott[5]，Yee[6]，李建瀛，等[7－8]，丁君，等[9]，Mondal，et al.[10]等都基于矩量法对波导裂缝天线阵列做了深入的研究分析。

有限元法特别适合于分析结构复杂以及不同媒质中的电磁问题，但是它需要在远离分析目标的地方设置吸收边界，所以它与矩量法一样难以解决电大尺寸问题。而有限元－边界元混合方法（FE－BI）能够把边界直接放置到分析目标的边界，这就大大降低了计算量，从而能够以有限的内存来精确分析大尺寸目标。

裂缝波导阵列的结构及其馈电网络虽然较为复杂，但是实际上，我们可以将其视作分布式的腔体来整体考虑。由于FE－BI法分析特殊结构大尺寸目标的有效性，采用它来分析计算波导裂缝天线阵列。在本文的分析中，以此为出发点建立了理论分析模型，波导裂缝阵列天线的计算被分成了两部分：体部分（波导内部及裂缝）和面部分（与裂缝上表面相关的部分），分别用有限元法和边界元法对这两部分进行分析。求解矩阵方程之后就可以由裂缝上的等效磁流计算得到波导裂缝阵列天线的远场方向图。通过对本文方法的数值计算结果与测试结果的比较，验证了本文方法的有效性。

2.理论方法

对于无限大地面上的三维腔体的散射问题，可以在腔体内部和口面上的电场建立泛函[11－12]，即

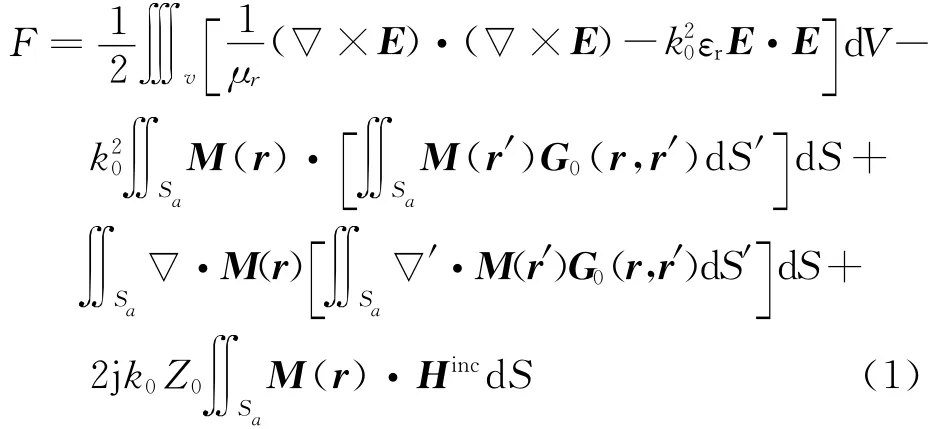
这里的V表示腔体的体积；Sa表示腔体口面的面积；M（r）表示口面上的等效磁流；Hinc是入射平面波的磁场；k0是自由空间的波数；Z0是自由空间的波阻抗；G0（r，r′）表示自由空间的格林函数。其中

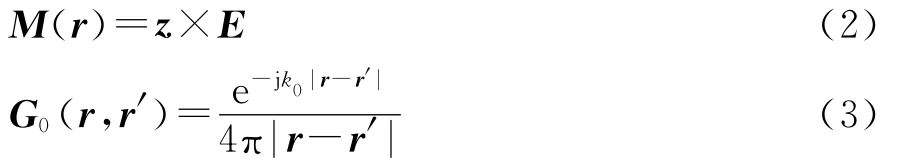
对式（1）中的泛函求驻点，把等效磁流用基函数展开并求解矩阵方程即可得到等效磁流。

把式（1）分解成与体部分（波导内部及裂缝）和面部分（与裂缝上表面相关的部分）：首先利用有限元法对体部分进行分析

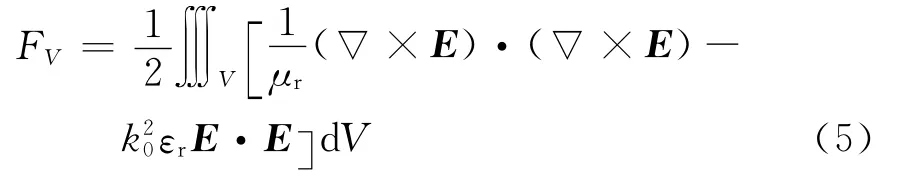
为了离散FV，可以把腔体V划分成若干小的体积单元（四面体或长方体），使用矢量基函数对腔体V内的电场进行展开然后求解。采用四面体单元来离散所研究的裂缝阵列天线的体部分。在每个体积单元（第e个单元）中，把电场展开为

对于每一个小的体积单元（小四面体），

式中Nv＝6，是四面体棱边的数目。

对于面部分（与裂缝上表面相关的部分），使用边界元法来分析

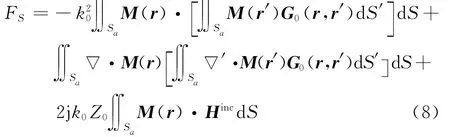
为了离散这些面积分，用三角形面元对式（2）中裂缝表面处的电场E进行展开，这样就能与选择的体单元的一个面相重合。引入下面的展开式

基函数Si的表达形式可参考文献[13] 。

然后对F（E）取变分，并使其为零。

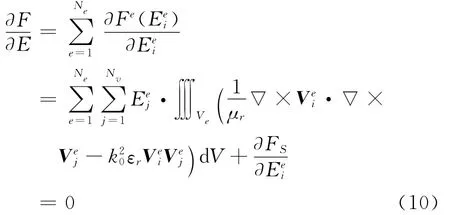
把公式（10）进一步细化即可建立一个求解电场展开系数的矩阵方程，由此即可得到波导裂缝上的等效磁流，根据等效磁流就可以通过计算得到波导裂缝阵列天线的远场方向图。

3.结果及分析

采用前面介绍的理论模型，用TE10模来激励波导。本文首先计算了文献[4] 中介绍的一个刻有7个缝的单根波导阵列天线。选用的波导型号为WR62（15.80 mm ×7.90 mm），其几何结构如图1所示。波导的壁厚t是1.0 mm.缝宽w是1.0 mm，缝的间隔ds为14.52 mm（1/2波导波长），缝的偏移量d为2.1 mm，裂缝长度l为9.99 mm.为了验证本文方法的正确性，我们把使用FE－BI法分析裂缝天线得到的计算结果与文献[4] 中的测量结果做了比较。图2中给出了在14.03 GHz频点上裂缝阵列天线的H面（yoz面）方向图。可以看出，计算结果与测量结果基本吻合，验证了本文方法的有效性。但是，在副瓣水平上，二者之间存在一定的差别，这是因为计算模型假设波导裂缝开口位于无限大导体平面上，没有考虑波导宽边的边缘效应。由于宽边纵缝波导的裂缝距离波导的边缘比较远，所以这种计算模型的精度是能够满足工程应用需求的。

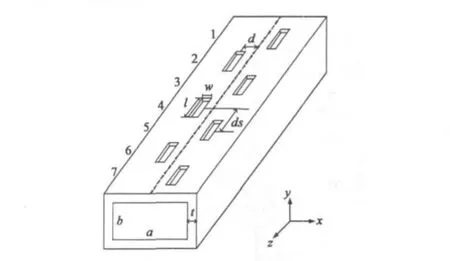
图1 开7个缝的单根波导的几何结构

第二个算例是8根波导组成的平面阵列，每个线性阵列单元都刻有6个纵向辐射裂缝，如图3所示。波导的尺寸是21.26 mm×5.08 mm，波导的壁厚t是0.81 mm，缝宽w是3.175 mm，缝的间距ds为22.28 mm，波导间的间距为1.02 mm.表1中给出了缝的偏移量和裂缝长度。在图4和图5中分别给出了在9.75 GHz频点上阵列天线E面（xoy面）和H面（yoz面）辐射方向图的计算值和测量值。计算值与文献[6] 中的测量值基本吻合，再次验证了本文方法的正确性和有效性。

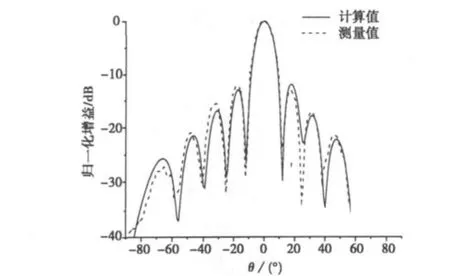
图2 开7个缝的单根波导的H面方向图

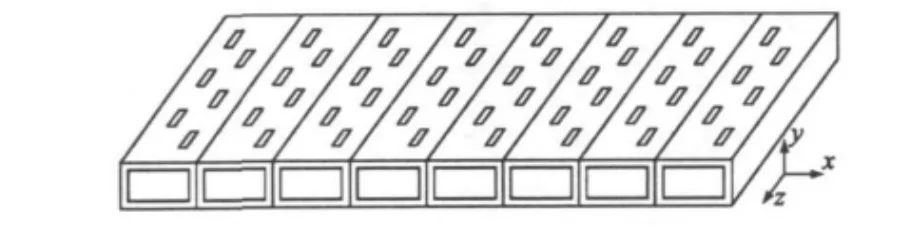
图3 6×8的波导阵列几何结构

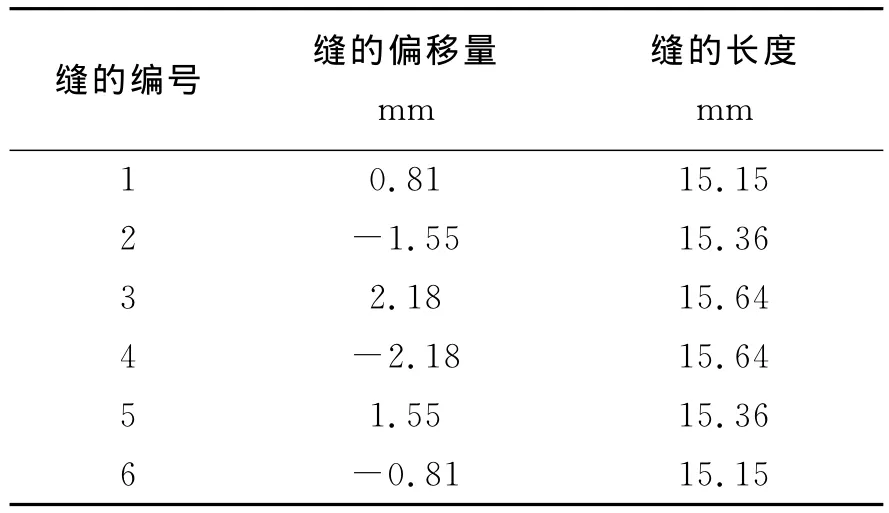
表1 偏移量和缝的长度

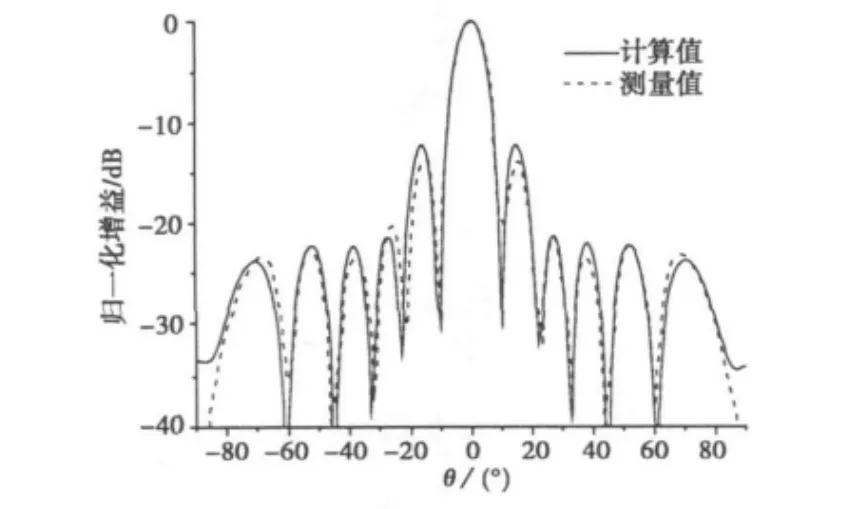
图4 6×8的波导阵列的E面方向图

图5 6×8的波导阵列的H面方向图

4.结 论

在本文中，我们将有限元－边界元法（FE－BI）引入到波导裂缝阵列天线的计算中，有效地解决了分析这类天线所需计算资源过大的问题。在建立理论分析模型的基础上，分别计算了单根波导裂缝天线和大型波导裂缝阵列天线，计算结果和测量结果吻合良好，验证了该方法分析波导裂缝阵列天线的可行性和有效性。

[1] KHAC T V.Solutions for some waveguide discontinuities by the method of moments[J] .IEEE Transactions Microwave Theory and Techniques，1972，20（6）：416－418.

[2] LYON R W，SANGSTER A J.Efficient moment method analysis of radiating slots in a thick－walled rectangular waveguide[J] .IEE Proceedings H Microwaves，Optics and Antennas，1981，128（4）：197－205.

[3] ELLIOTT R S，KURTZ L A.The design of small slot arrays[J] .IEEE Transactions Antennas and Propagation，1978，26（2）：214－219.

[4] HAMADALLAH M.Frequency limitations on broadband performance of shunt slot arrays[J] .IEEE Transactions Antennas and Propagation，1989，37（7）：817－823.

[5] GULICK J J，ELLIOTT R S.The design of linear and planar arrays of waveguide－fed longitudinal slots[M] .Ann Arbor Mich：UMI，1987.

[6] YEE H Y.The design of large waveguide arrays of shunt slots[J] .IEEE Transactions.Antennas and Propagation，1992，40（7）：775－781.

[7] 李建瀛，梁昌洪.矩形波导纵缝阵列的矩量法分析与设计[J] .电波科学学报，1998，13（4）：428－432.LI Jianying，LIANG Changhong.Moment method a－nalysis of rectangular waveguide longitudinal slot arrays[J] .Chinese Journal of Radio Science，1998，13（4）：428－432.（in Chinese）

[8李建瀛，梁昌洪.波导窄边等长双裂缝功率耦合机构实验研究 [J] .电波科学学报，1998，13（1）：52－54.LI Jianying，LIANG Changhong.Study of waveguide narrow wall equilong double－slots power couple structure[J] .Chinese Journal of Radio Science，1998，13（1）：52－54.（in Chinese）

[9] 丁 君，王旭刚，侯新宇，等.平面波导缝隙阵列的散射特性分析与计算[J] .电波科学学报，2008，23（6）：1051－1055.DING Jun，WANG Xugang，HOU Xinyu，et al.Scattering properties calculation and analysis of planar slotted waveguide array[J] .Chinese Journal of Radio Science，2008，23（6）：1051－1055.（in Chinese）

[10] MONDAL P，CHAKRABARTY A.Slotted waveguide antenna with two radiation nulls[J] .IEEE Transactions Antennas and Propagation，2008，56（9）：3045－3049.

[11] JIN J M，VOLAKIS J L.A finite element－boundary integral formulation for scattering by three－dimensional cavity－backed apertures[J] .IEEE Transactions Antennas and Propagation，1991，39（1）：97－104.

[12] JIN J M，LOU Z，LI Y J，et al.Finite element analysis of complex antennas and arrays [J] .IEEE Transactions Antennas and Propagation，2008，56（8）：2222－2240.

[13] RAO S M，WILTON D R，GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape[J] .IEEE Transactions Antennas and Propagation，1982，30（3）：409－418.