基于小波影响锥的天波雷达瞬态干扰抑制方法

周忠根 水鹏朗

（西安电子科技大学雷达信号处理国家重点实验室 陕西 西安710071）

1.引 言

天波超视距雷达（OTHR）工作在高频（HF）波段（3～30 MHz），不仅具有探测隐身目标的潜力，而且具有探测视距以外远程目标的能力。然而，极强的地（海）杂波和大量的外部干扰会严重地影响天波超视距雷达（OTHR）的性能。OTHR的外部干扰种类繁多，其中瞬态干扰主要是由流星余迹回波、闪电回波和人为的脉冲噪声引起的[1－2]。流星余迹回波是指流星余迹对OTHR反射的电磁波。一般流星分为流星雨和突发性的流星，流星雨只在一年中的某些时刻发生，而且会有预报。突发性的流星则经常出现，因此，OTHR中的流星余迹回波通常是指突发性的流星余迹产生的雷达回波，持续时间大约为零点几秒到几秒。在舰船检测的条件下，流星余迹回波的持续时间远小于相干积累时间，因此，在时域上可将其看作瞬态干扰。闪电回波的持续时间大约为200～400 ms，因此，在飞机检测（相干积累时间约为2～3 s）和舰船检测（相干积累时间约为10～50 s）时，闪电回波在时域上都属于瞬态干扰。瞬态干扰只对回波信号造成局部污染，即瞬态干扰只在若干个重复周期内出现，其持续时间短。但此类干扰强度大，在频域有很宽的谱，会掩盖目标信号。在频域这些干扰的存在会增加噪声基底，通常比OTHR的内部噪声高20～40 d B，从而导致雷达的检测性能极大地下降。因此长期以来，瞬态干扰抑制就是OTHR研究的一个热点问题。

目前，已有一些文献提出了各自的瞬态干扰抑制方法[2－10]，这些方法[2－6]原理基本类似。 一般分两步处理：首先，在时域确定瞬态干扰的位置，然后将干扰所在的数据点置为零；最后通过插值重构丢失的数据。对于数据重构，一般采用自回归（AR）模型的方式进行，其计算复杂度比较高，而且为保证预测误差达到最小，模型的阶数还须精心选择。目标的检测性能在很大程度上依赖于瞬态干扰抑制后的信号重构的质量。特别是当一个相干积累时间内存在多个瞬态干扰的情况下，如果将所有的瞬态干扰都挖除，那么剩余的数据量可能较少。这样利用AR模型对瞬态干扰挖除后的时段作数据重构时，将无法达到较好的重构效果，进而影响目标检测性能。文献[6] －[9] 提出利用小波变换来进行瞬态干扰抑制，主要基于以下原理：相对于地（海）杂波以及目标回波而言，瞬态干扰在短时间内包含了很强的能量，在时域上表现为突变（奇异）的特性。而小波变换可以有效地检测出信号的奇异点，因此，可以利用小波变换直接对时域信号的突变点进行检测。当瞬态干扰所在的时域位置确定后，该时段的数据将被挖除并重构。在利用小波变换检测信号突变点的基础上，提出了一种基于小波影响锥的瞬态干扰抑制方法。该方法利用离散平稳小波变换确定信号的奇异点（瞬态干扰），然后将每一奇异点对应的影响锥内的小波细节系数置零，即去除瞬态干扰。最后通过逆离散平稳小波变换重构数据。该方法无需抑制杂波，也不需要通过插值来重构数据。它在小波分解和重构中同时完成瞬态干扰的检测和数据重构，其计算量少，易于工程实现。对天波雷达实测数据处理表明该方法可以有效地抑制瞬态干扰。

2.基于小波影响锥的瞬态干扰抑制方法

2.1 信号奇异点的定位方法

通常用Lipschitz指数来描述函数的局部奇异性。设信号在点x0的邻域具有下列特性

其中

式中：h是一个充分小量；pn（x）是f（x）在x0点作Taylor级数展开的前n项，则称f（x）在x0点的Lipschitz指数为α，或称f（x）在x0点是Lipschitzα的。Lipschitz指数越大 ，函数越光滑。如果f（x）在x0点的Lipschitz指数小于1，则称f（x）在x0点是奇异的。Lipschitz指数与小波变换有密切的关系。若f（x）在x0点的邻域是Lipschitzα的，则存在K＞0，使得

即

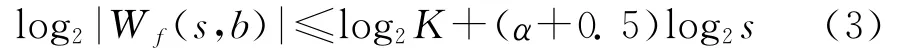
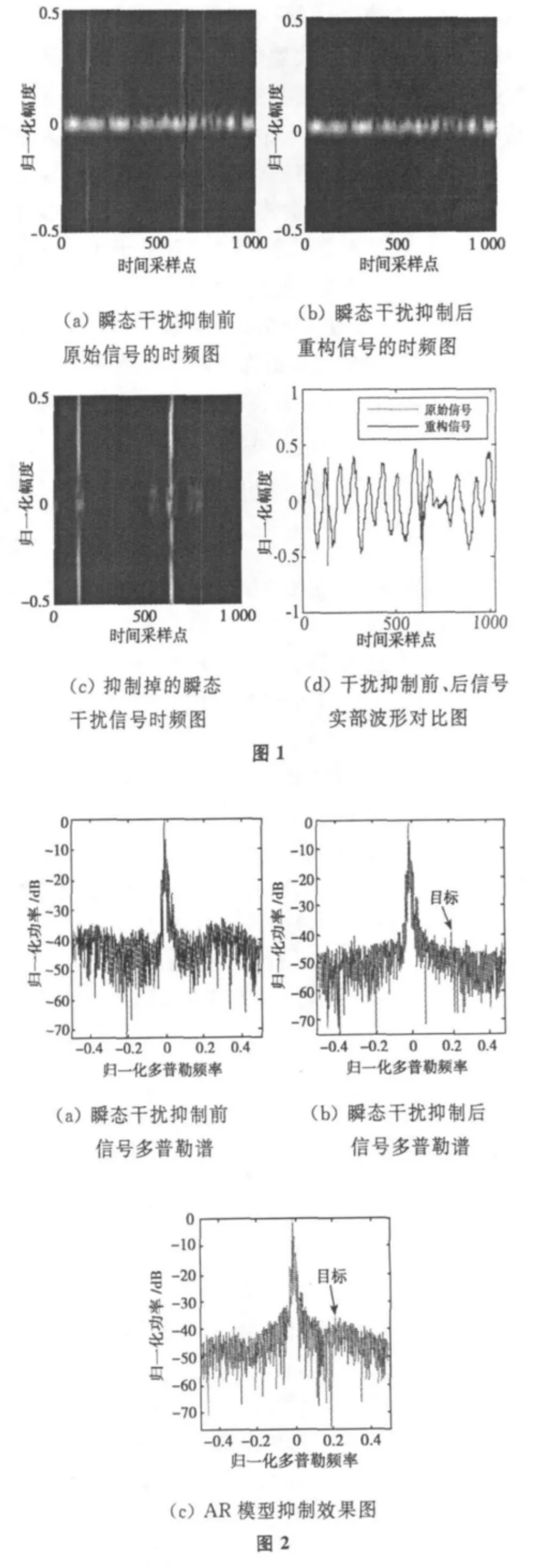
令

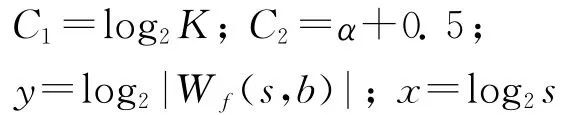
上式简化为

则可以利用一元线性回归方法解出C1，C2及K和α.

2.2 影响锥定义

设小波函数ψ具有紧支集[－C，C] 。在尺度－时间平面上，点v的影响锥是所有点（u，s）的集合，使得v含于的支集内。由于ψ（（t－u）/s）的支集为[u－Cs，u＋Cs] ，于是v的影响锥为｜u－v｜≤Cs.对一个连续信号进行小波变换，分解到各个尺度上的小波系数可以认为是由信号的不同点以及其前后的数据共同作用、影响区域相互叠加而成的。因此，某点的影响锥内的数据不仅反映了该点本身的特征，同时也反映了该点处信号前后数据变化的情况，这有助于确定该点的特性。

2.3 基于小波影响锥的瞬态干扰抑制方法

考虑到瞬态干扰通常只存在于一到两个距离或方位单元上，通过比较相邻多个单元的噪声基底就可以确定瞬态干扰存在的距离或方位单元，接下来需要进行瞬态干扰的抑制。由于瞬态干扰在时域上存在的时间远短于雷达相干积累时间且能量集中，因此，通常是在时域上进行瞬态干扰的检测和抑制。文献[6] －[9] 先利用小波变换来检测瞬态干扰（奇异点）的位置，然后把该时段的数据挖除且重构。同样利用小波变换检测信号突变点，提出了一种基于小波影响锥的瞬态干扰抑制方法。该方法利用离散平稳小波变换确定信号的奇异点（瞬态干扰），然后将每一奇异点对应的影响锥内的小波细节系数置零，即去除瞬态干扰。最后通过逆离散平稳小波变换重构数据。下面给出基于小波影响锥的瞬态干扰抑制方法的具体步骤：

1）对某一个距离单元的回波信号X＝｛x（1），x（2），…，x（N）｝，把X分成实部Xr和虚部Xi，选择合适的尺度（一般取值为4～6之间，处理实测数据时取为4。取值依据是由瞬态干扰的特点得出来的。瞬态干扰在时域上能量集中，持续时间短，其支集长度不会太长。通过分析实测数据，发现瞬态干扰经小波变换后在4～6层之间的支集长度与瞬态干扰的支集长度匹配得较好。），分别对实部Xr以及虚部Xi进行一维离散平稳小波变换得到Xrswt和Xiswt.这样，X的一维离散平稳小波变换为

2）估计奇异点的位置和各个尺度上奇异点的影响锥范围：

对Xswt的小波细节系数，在尺度J＝0上，求出它的模极大值和极大值所在位置。然后在这些极大值点上，对每一点利用前面所述的线性回归方法确定该点的Lipschitz指数α，由α值的正负来确定该点是否是奇异点（瞬态干扰的Lipschitz指数是负数，回波信号的Lipschitz指数是正数[6]）。如果是奇异点，就以奇异点的位置为基准，找出该点的影响锥范围。不妨设点v0是奇异点，所选用的小波函数必须是紧支撑的，其紧支集为[C1，C2] ，则在J（J＝1，2，3，4）尺度上点v0的影响锥范围为

式中：sJ＝2J是尺度系数。该范围与点v0是否是奇异点、小波函数的支集长度和小波尺度系数有关，而与瞬态干扰类型没有关系。

3）在每一个尺度上，分别把Xrswt和Xiswt中各个奇异点影响锥范围内的小波细节系数置为零，得到和，即

4）最后，分别对和作逆离散平稳小波变换重建信号，得到去除瞬态干扰后的回波信号，记为.

3.实测天波雷达数据处理

对采自OTHR的实测数据中含有瞬态干扰的某距离－方位分辨单元的回波信号先分成实部和虚部，分别进行一维离散平稳小波变换。实测数据中回波信号长度为1024，在小波变换中小波函数选db3小波，其支集长度为6。尺度取值4。然后按算法步骤2）来估计奇异点的位置和各个尺度上奇异点的影响锥范围。这里只给出较明显的第一处瞬态干扰的奇异点位置v0＝135，137，140。它们在各个尺度上的影响锥范围可用式（6）分别计算出来。

为了进一步说明提出的算法对实测数据的抑制效果，分别画出了原始信号、重构信号以及瞬态干扰的短时傅里叶变换时频图。图1（a）是瞬态干扰抑制前原始信号的时频图，可看出有两处瞬态干扰，这两处干扰的强度跟杂波的强度相比稍弱一些。图1（b）是瞬态干扰抑制后重构信号的时频图，可看出瞬态干扰完全得到了抑制。图1（c）是抑制掉的瞬态干扰信号的时频图，从图中可看出能检测到瞬态干扰信号并能确定它们的位置。该实测数据包含了两处较明显的瞬态干扰信号，一处大约在第120到第145个采样点之间，另一处大约在第630到第650个采样点之间。这也可从图1（a）和（d）看出来。图1（d）是瞬态干扰抑制前原始信号和干扰抑制后重构信号的实部波形对比图，幅度进行了归一化处理。综合图1（a）、（b）、（c）、（d），说明基于小波影响锥的方法对瞬态干扰抑制是有效的。

为检测算法的有效性，在实测数据里人为添加了一个归一化频率为0.216，信杂比为－40 dB的复正弦弱信号目标。分别利用基于小波影响锥的瞬态干扰抑制方法和传统的AR模型对其处理，结果如图2所示。由于目标幅度小于瞬态干扰幅度，在图2（a）的多普勒分布图上目标被瞬态干扰所掩盖。图2（b）为基于小波影响锥的瞬态干扰抑制方法处理后信号重构的多普勒谱图，可见目标很明显突出来了，瞬态干扰的抑制效果明显。图2（c）是用AR模型来恢复挖除数据后的多普勒图，这时目标突出不明显。另外，AR模型的数据重构效果跟模型阶数的选择有关。因此，须有一个判断准则来估计模型的阶数，比如可采用最后预测误差准则（FPE），使其一步预测的平均误差最小。对比图2（b）和图2（c）的处理效果可知：基于小波影响锥的瞬态干扰处理方法抑制效果更好。

4.结 论

提出了一种基于小波影响锥的天波超视距雷达瞬态干扰抑制方法，该方法避免了杂波抑制和插值重构，运算量小，实用性强。它在小波分解和重构中同时完成瞬态干扰的检测和数据重构，不需分两步完成。对天波雷达实测数据处理表明：该方法可以有效地抑制瞬态干扰。

[1] LIU Tao，GONG Yaohuan，WANG Jie，et al.OTHR impulsive detection in strong clutter background[C] //International Conference on Communications，Circuits and Systems，Milpitas，CA，23－25 July 2009：410－413.

[2] 邢孟道，保 铮，强 勇.天波超视距雷达瞬态干扰抑制[J] .电子学报，2002，30（6）：823－826.XING Mengdao，BAO Zheng，QIANG Yong.Transient interference suppressing in OTHR[J] .Acta Electron.Sinica，2002，30（6）：823－826.（in Chinese）

[3] 陈希信，黄银河.基于矩阵奇异值分解的高频雷达瞬态干扰抑制[J] .电子与信息学报，2005，27（12）：1879－1882.CHEN Xixin，HUANG Yinhe.A SVD－based approach of suppressing transient interference in High－Frequency radar[J] .Journal of Electronics ＆ Information Technology，2005，27（12）：1879－1882.（in Chinese）

[4] LIU Tao，WANG Jie，CHEN Xiaoxu，et al.OTHR impulsive interference characteristics and detection based on AR model[C] //2009.International Conference on Communications，Circuits and Systems，Milpitas，CA，23－25 July 2009：810－814.

[5] 王 阶，刘 涛，陈晓旭，等.天波超视距雷达流星余迹瞬态干扰抑制方法[J] .电子测量与仪器学报，2009，23（10）：67－71.WANG Jie，LIU Tao，CHEN Xiaoxu，et al.Method of meteor trail impulsive interference suppression in OTHR[J] .Chinese Journal of Radio Science，2009，23（10）：67－71.（in Chinese）

[6] 权太范，李健巍.高频雷达抗瞬时干扰研究[J] .现代雷达，1999，21（2）：l－6.QUAN Taifan，LI Jianwei.A study on high frequency radar suppressing sudden interference[J] .Modern Radar，1999，21（2）：l－6.（in Chinese）

[7] 强 勇，侯 彪，焦李成，等.天波超视距雷达抑制流星余迹干扰方法的研究[J] .电波科学学报，2003，18（1）：23－27.QIANG Yong，HOU Biao，JIAO Licheng，et al.An approach of suppressing meteor trail interference in over－the－horizon radar[J] .Chinese Journal of Radar Science，2003，18（1）：23－27.（in Chinese）

[8] GODFREY S E.The removal of transients from OTH radar signals via wavelets[C] //1994 Conference Record of the Twenty－Eighth Asilomar Conference on Signals，Systems and Computers，Pacific Grove CA USA，1994，Oct.－Nov，1080－1084.

[9] 黄 亮，文必洋，邓 巍.高频地波雷达抑制瞬态干扰研究[J] .电波科学学报，2004，19（2）：l66－170.HUANG Liang，WEN Biyang，DENG Wei.Suppressing instantaneous interference of high frequency ground wave radar[J] .Chinese Journal of Radar Science，2004，19（2）：l66－170.（in Chinese）

[10] 苏洪涛，保 铮，张守宏.自适应地波超视距雷达高频通信干扰抑制[J] .电波科学学报，2003，18（3）：270－274.SU Hongtao，BAO Zheng，ZHANG Shouhong.A－daptive HF－communication interference mitigation in HF－GWR[J] .Chinese Journal of Radar Science，2003，18（3）：270－274.（in Chinese）