改善单相矩阵变换器失真的电路仿真*

王建华， 高海生

(华东交通大学电气与电子工程学院，江西南昌 330013)

0 引言

在当前，现代电力电子技术、微电子技术及电动机控制技术的进步使得交流调速用变频传动技术得到了巨大发展，加强了交流传动在电力传动领域中的主导地位，因此变压变频电源－脉宽调制(Pulse Width Modulation，PWM)变频器成为炙手可热的电子产品。这种变频器的主电路几乎都是“交－直－交”变换。在赢得可观效益的同时，这种变频器也带来了谐波污染、功率因数低、直流滤波电容寿命有限等不良影响。在这种情况下，从事电力电子技术研究开发的人们开始探讨各种新的变频电源，矩阵变换器应用而生。矩阵变换器是一种崭新形式的、具有通用性的电力电子变换器，可以实现对交流电诸要素如相位、幅值、频率等进行交换。目前研究的矩阵变换器多集中在三相，但是由于目前偏远地区、小型工业部门和家庭等小容量电力用户，基本采用单相供电;甚至在轨道交通的电力牵引中也采用单相供电［1］，所以本文主要针对单相矩阵变换器输出波形失真改进进行相关的理论研究。

1 单相矩阵变换器拓扑结构与仿真

单相矩阵式变换电源的电路拓扑结构［2］如图1所示。图中S11～S22为4只理想的双向开关，由2只绝缘栅双极晶体管(Insulated Gate Bipolar Transistor，IGBT)与二极管反并联构成，通过一组开关函数将输入的工频交流电转换成输出电压和频率可调的单相交流电。

通过能量守恒的原则和对单相矩阵变换器的理论研究，可得出输出电压与输入电压之间的关系如下:

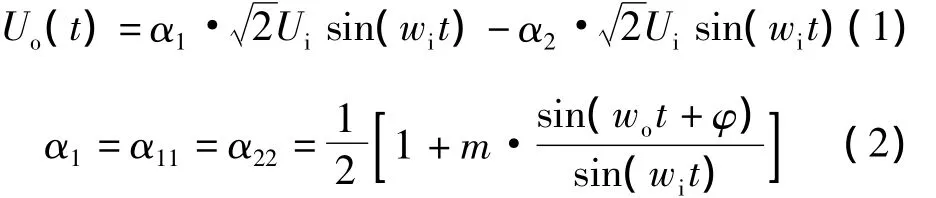
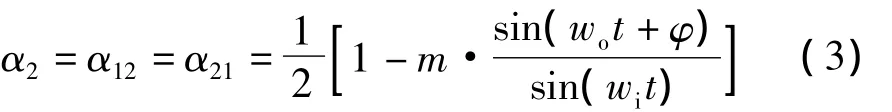
式中:m——电压传输比，m=Uo/Ui;

α11——双向开关 S11的占空比，其他以此类推。

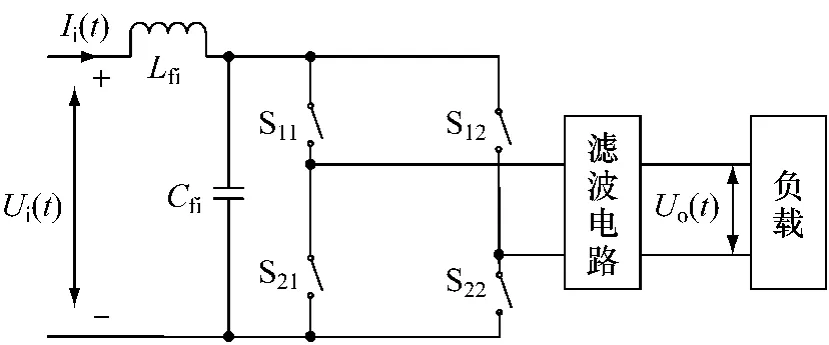
图1 单相矩阵变换器拓扑结构

实时求解式中m的变化，并用αij控制对应的矩阵开关Sij在每个周期内的占空比，即可实现AC-AC转换。

采用MATLAB仿真软件从传递函数角度去反映单相矩阵变换器的解析特性，可得到占空比和输出波形如图2、图3所示。

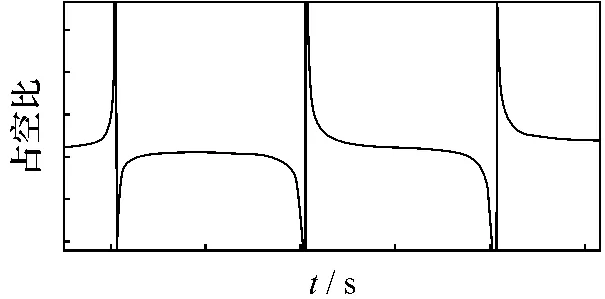
图2 占空比α11波形图

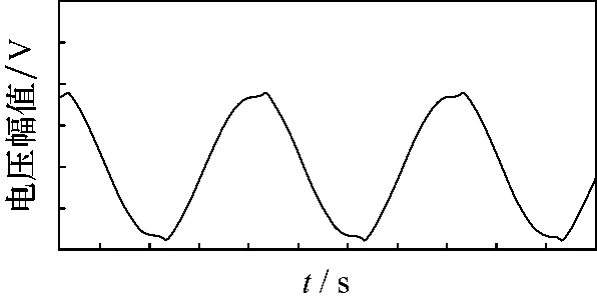
图3 单相矩阵变换器输出波形

2 输出波形失真原理的分析

通过对单相矩阵变换器的仿真研究发现:单相矩阵变换器能实现交流到交流的变频与变压的功能。输出波形在一个周期内出现了两次“内凹”的失真，而且每次都是在输出波形峰值处。该失真与输入电压过零有关，对照仿真的α瞬时波形图，其瞬时值超出约束条件，出现α＞1和α＜0就会出现失真［3］。因此要想办法去改进波形，消除失真，最终得到完美的波形。要想达到这个目的，首先要分析出产生输出波形失真的原因。

单相矩阵变换器输出波形失真主要从以下两个方面进行分析。

(1)从输入电压/输出电压的波形来分析。

输出电压Uo(t)波形不失真时应始终在输入电压Ui(t)包络线范围之内。从图4波形中可看出输出电压波形出现失真的区间正是输出电压超出输入电压的包络线的区间。

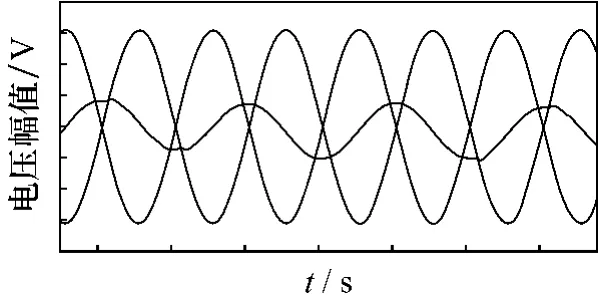
图4 单相矩阵变换器输入/输出波形图

(2)从能量角度去分析。从能量守恒原则得知:当输入电压Ui(t)过零时，输出电压Uo(t)必为零。当wo、wi不相关时，此时期望输出Uo'(t)(通过矩阵开关调制，期望矩阵变换器输出无失真正弦电压)并不一定为零，此时矩阵变换器能够实际传输的能量少于通过输出期望波形计算所必须的能量。因此产生输出波形失真。

单相矩阵变换器出现失真的原因就是输入的瞬时能量达不到期望的输出能量，所以要想改变输出波形的失真，就要使输出波形出现失真时的输入能量增加，使其达到期望的输出能量即可。

3 改进后的电路结构原理图

单相矩阵变换器输出波形出现失真的原因在于输入能量瞬时值达不到理论计算所需的期望输出能量值，因此只有在单相矩阵变换器的拓朴结构上有所改变，才可能减小和消除输出波形失真［4］。

波形失真与α的大小有关，当实时运算得0＜αij＜1范围时，期望输出波形一定低于输入波形的包络线。电源经调制函数控制下的开关矩阵向负载提供能量。矩阵开关和负载直接从电源得到能量，保持正弦输出，无需辅助环节的帮助也能保持理想的正弦波形的期望输出，同时将输入的部分能量存储于一个能量补充元件中，在本文中，能量补充元件采用的是电容。

当αij≥1和αij≤0时，期望输出波形一定超出输入波形的包络线。为了解决波形失真的问题，将存储能量元件中的能量释放出来，以补充能量的不足。

根据上述思路，画出具有校正波形失真的电路结构如图5所示。

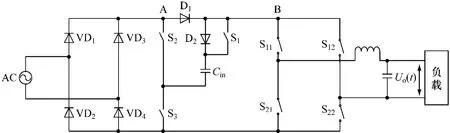
图5 改进后单相矩阵变换器的电路结构

该电路由三部分组成:二极管组成的整流电路;Cin的吸收和释放能量的电路;双向开关矩阵电路。整流电路采用桥式整流，将输入的交流正弦波变为直流的脉动波形，单向脉动输入可以使用单极性电容，减少装置体积，提高功率密度。如果不采用桥式整流，则需要两组由电容吸收和释放能量的电路。Cin的吸收和释放能量的电路主要用于改善和弥补单相矩阵变换器输出波形的失真。从图中可看出，它由三个开关S1、S2和S3，两个二极管D1、D2和能量吸放电容Cin组成。根据期望输出波形与输入波形电压相对大小，将电容的吸收和释放能量的电路分为3个工作区间，储能元件处于充电－保持－放电的循环状态，如图6所示。

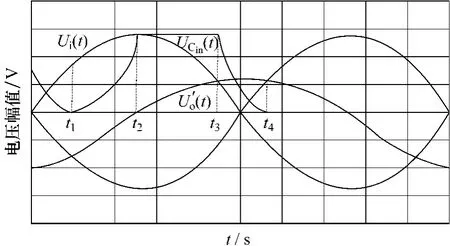
图6 储能电容电压UCin(t)充放电电路图

当Uo'(t)≤Ui(t)时，电容吸收能量(t1～t2)和电容能量保持(t2～t3)，对应的开关S3闭合、S2断开。

当Uo'(t)＞Ui(t)时，电容放电，提供能量，校正波形的失真。对应的开关S1、S2闭合，开关S3断开。电容Cin与电源串联，两者提供的能量之比取决于它们的电压之比。

在校正波形失真的单相矩阵变换器中有两类控制信号。

(1)根据能量控制环节采样，在电容充电和保持时间内利用式(2)、式(3)计算出电容充放电中的电路的控制开关S1、S2、S3的占空比。在这区间内输入和期望电压的关系应保持在Uo'(t)≤Ui(t)，如图6 所示，占空比0 ＜αij＜1，对应的开关S3闭合，开关S1、S2断开。当输入电压和期望输出电压关系为Uo'(t)＞Ui(t)时，占空比αij＜0 和 αij＞1，对应的开关 S1、S2闭合，S3断开。

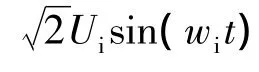
这时应用式(4)、式(5)来计算双向开关的占空比控制开关矩阵。通过斩波调制生成输出波形Uo(t)，此时通过该电路的校正，实际输出Uo(t)值应近似等于期望输出Uo'(t)值。

4 仿真结果

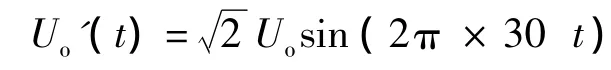
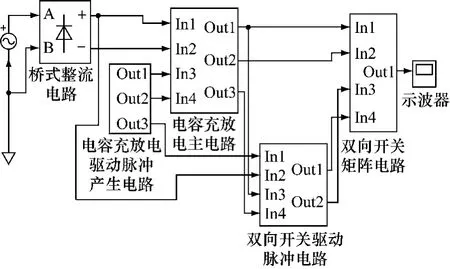
图7 改进后的单相矩阵变换器的数学模型

从图7来看，模型中总共包括了5个子系统，桥式整流电路、电容充放电主电路、双向开关矩阵电路、电容充放电驱动脉冲产生电路、双向天关驱动脉冲电路，其中的桥式整流电路将输入的交流电压源整流成单相脉动波形，电容充放电主电路用来模拟电容充放电，双向开关矩阵电路用来模拟主电路中的四个双向开关。对于这个模型最关键的还是驱动脉冲的生成。这个电路中总共有两部分，一部分就是要产生驱动电容充放电电路中的开关的驱动脉冲，也就是图中的电容充放电驱动脉冲产生电路环节，其作用就是要产生所需要的脉冲，脉冲产生的一个关键依据就是输入电压和输出电压的差值，通过上面的分析知道，当输出电压小于输入电压时，开关S3导通，S1、S2截止，所以要给S3一个开通脉冲而给S1、S2一个截止脉冲。当输出电压大于输入电压时，开关S3截止，S1、S2导通，所以要给 S3一个截止脉冲而给S1、S2一个开通脉冲。另一部分驱动脉冲是针对主电路双向开关的。下面给出了期望输出

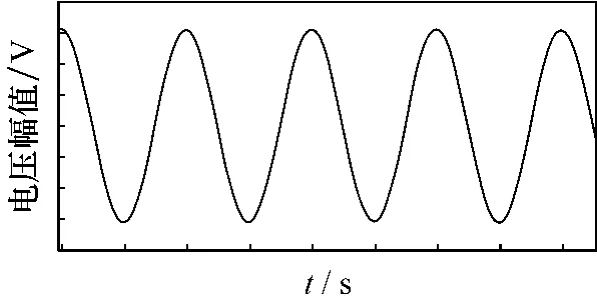
图8 输入波形图

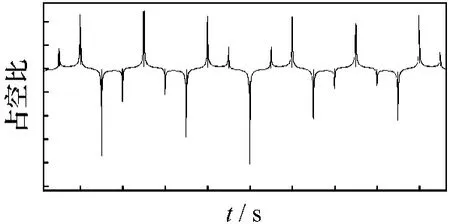
图9 占空比波形图

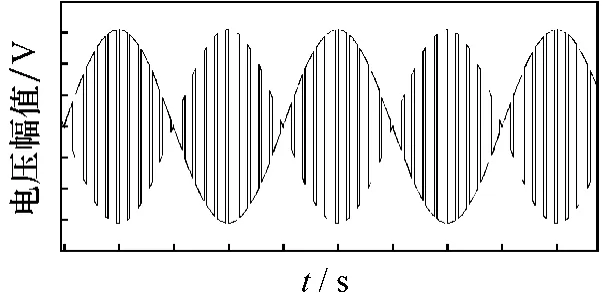
图10 滤波前的输出电压波形图

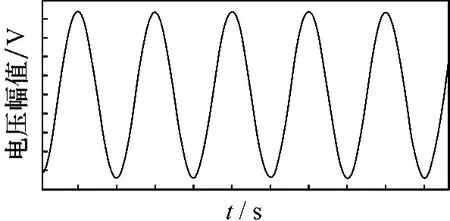
图11 滤波后输出电压波形图

从波形图中可看出，曲线比较光滑，基本接近理想的正弦波，与给定的期望输出电压波形接近，达到了预期的效果。单相矩阵变换器拓扑结构简单，理论上，一定范围内的输出电压，整个范围内的输出频率连续可调，输出波形完美，并能够完全传递电源电压。另外，它本身不产生谐波污染，同时又能够对电网进行无功补偿，其总体性能高于其他变换器。在日益关注可持续发展问题，大力推行电力环保、绿色电源的今天，研究与开发这种变换器就特别具有现实意义，发展前景良好。

［1］陈伯时.矩阵变换器的发展与展望［J］.电工技术，2003(1):57-58.

［2］王勇.矩阵变换器的空间矢量调制［J］.系统集成及应用研究，2005:34-50.

［3］康现伟.基于双空间矢量调制的矩阵变换器的研究［D］.武汉:华中科技大学，2006.

［4］万衡.单相矩阵式变换器的研究与应用［D］.南昌:华东理工大学，2001.

［5］蔡文.基于MATLAB单相－单相(MC)的研究［J］.驱动与传动，2004:122-124.

［6］洪乃刚.电力电子和电力拖动控制系统的MATLAB仿真［M］.北京:机械工业出版社，2006.

［7］陈武，王付胜，张兴，等.基于新型调制策略的三相-单相矩阵变换器研究［J］.电力电子技术，2010，44(10):29-31.

［8］李鹏程，吴雷，袁碧金.矩阵式三相/单相电源研究［J］.现代电子技术，2010，33(8):205-207.