基于强跟踪滤波算法的异步电机参数自适应无速度传感器控制*

陆 可

(西南交通大学电气工程学院，四川成都 610031)

0 引言

现代工业控制中，异步电机以其结构简单、运行可靠、价格低廉、维护方便等优点得到了广泛应用，而其固有的强耦合、非线性、多输入、多输出等特性使其成为一类重要的非线性控制系统。目前，对于异步电机控制的研究主要集中在磁场定向控 制［1］、直 接 转 矩 控 制［2］、反 馈 线 性 化 控制［1，3］、滑模控制［4］及无源性控制［1］等方法上，它们的共同点就是力求转矩和磁链的独立控制，从而实现异步电机的线性化控制。

在异步电机无速度传感器控制系统中，除了采用一定的控制方法外，电机参数的准确与否是影响其控制性能的主要因素。但是，异步电机在运行过程中，参数随着工况和环境的变化表现出时变性，在利用定参数模型进行计算时，必然会引入误差，导致控制性能变差。因此，电机参数的在线辨识得到了广泛研究，其中大多数方法都是利用约束条件，简化模型结构，减少测量变量，得到电机参数;也有利用模型参考自适应［5-6］、观测器估计［7-8］(Luenberger、Kalman 等)、人工智能［9－11］(包括神经网络、模糊逻辑、遗传算法等)等算法实现电机参数的在线辨识。

此外，还有难点来自于未知的负载扰动，以及在极低速和零速时的转速估计问题［12］。因此，需要设计一种估计方法，能同时估计电机转速、转子磁链、负载转矩和电机参数，并能解决零速附近的转速估计问题。文献［7］在异步电机四阶模型的基础上，引入机械和转矩方程，同时为了在线辨识转子电阻，增加负载转矩和转子电阻为状态变量，建立异步电机的七阶扩展状态方程，并利用扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法，实现异步电机状态和转子电阻的同时估计。

EKF算法是一种常用的状态估计方法，但存在两大缺陷:(1)关于模型不确定性的鲁棒性差，造成状态估计不准，甚至发散等现象;(2)当系统达到平稳状态时，算法将丧失对突变状态的跟踪能力。针对上述两个问题，周东华在EKF算法的基础上提出了强跟踪滤波(Strong Track Filter，STF)［13－14］算法，利用正交性原理，增加渐消因子，使算法始终保持对系统状态的准确跟踪，从而有效弥补了EKF算法的缺陷。因此，本文利用STF算法替代EKF算法对电机状态和参数进行估计，并通过仿真对两者的估计性能进行了比较。

1 异步电机数学模型

在静止αβ坐标系下，异步电机的四阶离散化模型可描述为

状态 向 量 x(k)= ［isα(k)isβ(k)ψrα(k)ψrβ(k)］T，输出向量 y(k)=［isα(k)isβ(k)］T，输入向量 u(k)=［usα(k)usβ(k)］T，系数矩阵分别为

式中:us、is——定子电压、电流;

ψr——转子磁链;

Rs、Rr，Ls、Lr——定、转子电阻、电感;

Lm——励磁电感;

ωr——转子角速度;

T——采样周期。

τr——转子时间常数，τr=Lr/Rr;

σ——漏感系数，σ =1－Lm2/LsLr;

为利用STF算法对电机转速、负载转矩和转子电阻进行估计，根据文献［7］在原四阶模型的基础上引入机械和转矩方程，并增加状态变量ωr、TL和 Rr，则扩展后的状态向量 x(k)=［isα(k)isβ(k)ψrα(k)ψrβ(k)ωr(k)TL(k)Rr(k)］T，输入和输出向量不变。同时，修改系数矩阵为

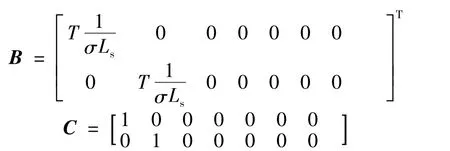
式中:TL——负载转矩;

J——转子及其所连接负载的转动惯量;

np——极对数。

2 STF算法

根据上述异步电机的非线性模型，可利用STF算法对其状态进行估计。按照实际系统模型，在式(1)和式(2)的基础上增加噪声项，重写状态方程为

式中，状态噪声w和测量噪声v均为高斯白噪声，并具有如下统计特性:E［w(k)］=E［v(k)］=0，E［w(k)w(j)T］=Q(k)，E［v(k)v(j)T］=R(k)，E［w(k)v(j)T］=0。其中，Q(k)为对称非负定阵，R(k)为对称正定阵。初始状态x(0)为高斯分布的随机向量，且满足如下统计特性:E［x(0)］=x0，E［x(0)－x0］［x(0)－x0］T=P0，并且 x(0)与 w(k)，v(k)统计独立。

根据文献［13］，带多重次优渐消因子的STF算法的迭代步骤如下:

(1)令k=0，设置初始值x(0|0)、P(0|0)，以及噪声协方差阵Q、R。

(3)由式(9)计算出测量残差γ(k+1);由

式(10)计算出其协方差阵V(k+1)。式中ρ为遗忘因子，0 ＜ρ≤1，一般取 ρ=0.95。

(4)由式(11)～式(15)计算出渐消矩阵LMD(k+1);式(11)中，β≥1为弱化因子，用于削弱渐消因子的调节作用，避免可能造成的过调节，使状态估计更加平滑;式(12)和式(14)中，ai为预先确定的常数，根据系统的先验知识可大致确定:

(5)由式(16)计算出状态误差协方差阵预测值P(k+1|k);由式(17)得到增益矩阵K(k+1)。

(6)由式(18)和式(19)更新状态及其误差协方差阵的估计值(k+1|k+1)、P(k+1|k+1)。

(7)k+1→k，转向(2)，继续循环。

3 仿真结果比较及分析

为检验STF算法的估计性能，下面通过图1所示的异步电机无速度传感器矢量控制系统对其进行仿真研究，并与EKF算法在估计精度和跟踪速度等方面进行比较。算法仿真采用Simulink实现，利用S-Function分别编写基于STF和EKF算法的估计模块。图中ASR、ATR和AψR分别为转速、转矩和磁链PID调节器，实现带转矩内环的转速和磁链闭环控制。仿真所用电机为三相四极笼型交流异步电机，星型联接，其参数如下:PN=2.2 kW，UN=380 V，fN=50 Hz，nN=1 440 r/min，J=0.01 kg × m2，Rs=1.7 Ω，Rr=2.0 Ω，Ls=166 mH，Lr=168 mH，Lm=159 mH。为了避免各物理量的数值差异导致数值计算的不稳定，本文在仿真中将各物理量均转换成标幺值进行计算。

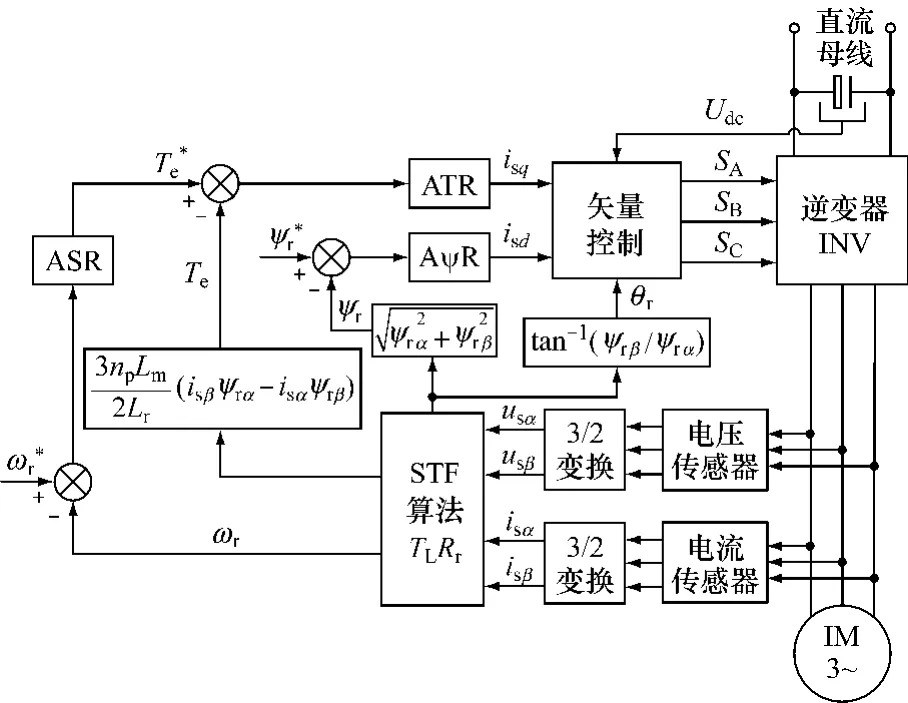
图1 无速度传感器矢量控制系统

在EKF和STF算法中，系统初始状态误差协方差阵P(0|0)、噪声协方差阵Q、R的取值对算法的性能有一定的影响。为了减小算法的计算复杂度，P(0|0)、Q和R的取值均为正定的对角阵。根据Kalman滤波算法，Q和R的取值应分别依照状态和测量噪声的统计特性获得。但是，实际系统中噪声的统计特性并不一定能得到，因此，Q和R的最优取值经常是通过经验和多次试验后反复调整得到的。本文综合考虑算法的动态响应、收敛速度、稳态精度等因素，通过多次调整得到最优取值为 P(0|0)=10－7I(7)，Q=10－7I(7)，R=10－5I(2)。为了保证 EKF 和 STF算法在相同的条件下进行比较，两者的P(0|0)、Q和R取值相同，且状态向量的初始值均为零。为了综合比较EKF和STF算法在各种工况下的估计性能，设计仿真过程如表1所示。

表1 仿真过程描述

图2分别给出了转子电阻((a)、(b))、电机转速((c)、(d))、负载转矩((e)、(f))和转子磁链((g)、(h))的估计值及其对应误差值的仿真波形，其中REF表示实际值或给定值，EKF和STF分别表示对应的估计值。下面针对EKF和STF算法的估计性能进行比较分析。

(1)转子电阻。由图2(a)、(b)可见，STF算法能有效估计转子电阻，当转子电阻发生突变时，STF算法的动态调节时间在2 s以内。0～15 s内的稳态误差约为5%，在最后5 s的零速阶段，稳态误差达到了50%，这与零速时激励信号不够充分有关。从转速、负载转矩及转子磁链的估计结果来看，由于STF算法对于系统的不确定性具有较强的鲁棒性，因此这些误差是在可以接受的范围之内。但是EKF算法无法正确估计转子电阻，对于转子电阻的突变不能做出灵敏响应，而是需要一个较长的估计过程，这将影响算法对于转速、负载转矩和转子磁链的估计性能，导致产生较大的误差。

图2 基于EKF和STF算法的仿真结果

(2)电机转速。由图2(c)、(d)可见，电机在加速和减速过程中，STF算法均能很好地跟踪转速的阶跃变化。在状态突变初由于转子电阻估计未稳定，因此转速估计有明显误差。当转子电阻被准确估计后，转速就能快速达到准确值。其动态响应时间也在2 s以内，并且在高速时稳态误差达到1%以内，低速和零速时也在2%左右。EKF算法的转速估计性能相对较差，主要是由于转子电阻的估计误差较大。相对于STF算法，EKF算法估计转速的动态过程较长，约需要4 s，稳态精度较低，误差达到了10%，甚至更大，不能满足控制要求。

(3)负载转矩。由图2(e)、(f)可见，和转速估计性能类似，由于转子电阻的准确估计，STF算法对于负载转矩也有满意的估计结果，动态过程在2 s以内，且稳态精度很高，误差几乎为零，这也保证了零速时的转速估计具有较高的精度。EKF算法在估计负载转矩时同样具有较高的稳态精度，但动态时间很长，需要4 s以上，这严重影响了转速的估计性能。

(4)转子磁链。由图2(g)、(h)可见，转子磁链给定值为1 Wb，转速和负载转矩的突变引起了转子磁链扰动，STF和EKF算法均能跟踪这些扰动。但是，相比之下，STF具有更理想的估计性能，STF算法的动态过程保持在2 s以内，而EKF则约需4 s。同时，两者都具有较高的稳态精度，稳态误差均在1%以内，保证了磁场的准确定向。

综上所述，STF算法对突变状态具有强跟踪能力，能快速且准确地跟踪转子电阻的突变，从而保证了转速、负载转矩和转子磁链的精确估计，满足矢量控制的要求。EKF算法对突变状态的跟踪能力则较差，因此在估计性能上不如STF算法。此外，负载转矩的估计使得算法在零速附近也具有满意的估计性能。

4 结语

本文利用STF代替EKF算法实现异步电机的状态估计和转子电阻辨识，通过仿真比较了STF和EKF算法的估计性能。仿真结果表明，STF算法能有效辨识转子电阻的变化，从而保证电机转速、负载转矩和转子磁链的准确估计;STF算法在估计精度、跟踪速度和动态响应等方面均优于EKF算法;电机模型中机械和转矩方程的引入，以及负载转矩作为状态变量进行估计，使得电机在极低速和零速下运行时，算法也能得到理想的转速估计性能。目前，主要解决了转子电阻的辨识问题，但是定子电阻及电感参数在电机运行过程中同样具有时变性，并且更加复杂，需要进一步研究和试验。

［1］Bujag G S，Kazmierkowski M P.Direct torque control of PWM inverter fed AC motors a survey［J］.IEEE Trans on Industrial Electronics，2004，51(4):744-757.

［2］Takahashii I，Noguchi T.A new quick-response and high-efficiency control strategy of an induction motor［J］.IEEE Trans on Industry Application，1986，22(5):820-827.

［3］Novotnakr T，Chiasson J，Bodson M.High-performance motion control of an induction motor with magnetic saturation［J］.IEEE Trans on Control System Technology，1999，7(3):315-327.

［4］Sabanovica A，Izosimov D B.Application of sliding modes to induction motor control［J］.IEEE Trans on Industry Application，1981，IA-17(1):41-49.

［5］冬雷，李永东，王文森，等.矢量控制中感应电动机转子电阻的自适应辨识［J］.电工技术学报，2002，17(4):13-17.

［6］金海，黄进.基于模型参考方法的感应电机磁链的自适应观测及参数辨识［J］.电工技术学报，2006，21(1):65-69.

［7］Barut M，Bogosyan S，Gokasan M.Speed sensorless direct torque control of IMs with rotor resistance estimation［J］.Energy Conversion and Management，2005，46(3):335-349.

［8］黄志武，桂卫华，年晓红，等.一种新型的基于观测器的无速度传感器感应电动机定子电阻辨识方案［J］.电工技术学报，2006，21(12):13-20.

［9］汪镭，周国兴，吴启迪.基于Hopfield神经网络的线性系统参数辨识方案及在鼠笼式电机传动系统参数辨识中的应用研究［J］.中国电机工程学报，2001，21(1):9-11.

［10］Karanayilb B，Rahman M F，Grantham C.Stator and rotor resistance observers for induction motor drive using fuzzy logic and artificial neural networks［J］.IEEE Trans on Energy Conversion，2005，20(4):771-780.

［11］黄开胜，童怀，郑泰胜，等.遗传算法在异步电动机动态模型参数识别中的应用［J］.中国电机工程学报，2000，20(8):37-41.

［12］Holtz J.Sensorless control of induction machines-With or without signal injection［J］.IEEE Trans on Industrial Electronics，2006，53(1):7-30.

［13］周东华，叶银忠.现代故障诊断与容错控制［M］.北京:清华大学出版社，2000.

［14］周东华，席裕庚，张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器［J］.自动化学报，1991，17(6):689-695.