小型独立系统中同步发电机的数字仿真

陈成功， 史伟伟， 李金华

(1.上海交通大学电子信息与电气工程学院，上海 200240;

2.中船重工711研究所，上海 201108)

0 引言

在船舶、自供电工矿企业等小型独立系统中，同步发电机作为系统电能的来源，其动态运行特性是整个系统分析的基础和核心。因此，在对小型独立系统进行仿真分析时，建立合适的同步发电机数学模型，对系统的仿真精度和动态性能分析有着重要影响。

由于同步发电机自身的特点，用于仿真的同步发电机数学模型一般由建立在dq坐标系下的方程组进行描述，dq坐标系与转子保持同步，这样可以消除方程组中的变系数，大大减少仿真模型分析和计算的难度。常见的同步发电机仿真模型是一个七阶模型，又称为基本模型，模型由五阶的电路方程和两阶的转子运动方程所组成［1］。基本模型是同步发电机仿真中应用非常多的一种模型［2-3］，这是因为其他仿真模型都是在基本模型的基础上，根据不同的假设条件推导而来的。因此，基本模型在所有仿真模型中具有最高的仿真精度，理论上最接近同步发电机动态运行特性，但是同时模型的阶数也最高。对于一个含有上百台发电机的多机电力系统，若再加上其励磁系统、调速机和原动机的动态方程，将会出现“维数灾”，给分析计算带来极大的困难［4］。因此，在实际工程问题中，常会采用不同程度简化的导出模型，在满足不同场合仿真需要的同时，减少仿真所需的计算量和时间。导出模型又称为实用模型，按照阶数的不同，可分为六阶至三阶等不同形式，阶数越低，仿真精度相对也越差。文献［4，5］详细介绍了各阶导出模型的推导过程，文献［6］则对不同阶次的导出模型进行了分析和比选，并对六阶和两阶模型进行了三相短路故障的暂态稳定性仿真。

1 数学模型的确立

小型独立系统在系统内发电机台数不多、系统构成不是很复杂的情况下，可选用阶数较高的模型，能保证一定的仿真精度。但在大多数情况下，考虑到电机的暂态过程中，相比于几秒甚至十几秒的机械过渡过程和百毫秒级的励磁绕组暂态，忽略定子绕组的暂态过程，对系统中其他部分仿真结果的影响非常小，所以一般选用五阶以上的模型就足够满足仿真的精度要求。

小型独立系统仿真中对所建的同步发电机模型的另外一个要求是能灵活地改变电机模型的输入输出量，以便于不同情况下的仿真要求，采用七阶基本模型很难做到这一点。在使用绕组电流作为输入量、电压作为输出量时，仿真环节中会出现微分项，容易导致不期望的仿真结果出现。

综上考虑，在对几种模型进行比较分析之后，决定采用忽略定子绕组暂态的5阶模型来作为同步发电机的数学模型，即认为在仿真过程中，定子电压方程中pΨd=pΨq=0。简化的同步发电机5阶模型可由式(1)～式(7)表示如下［4］:

式(1)～式(7)中的参数采用标幺值表示同步发电机惯用参数，优点是可以直接和工厂设计参数相匹配，而无需再进行换算。

式中:ud、uq——发电机定子 d、q 轴端电压;

id、iq——发电机定子 d、q 轴电流;

Ef——定子励磁电动势;

E'q，E″q——电机 q 轴电动势，超瞬变电动势;

E″d——d 轴超瞬变电动势;

Xd——d 轴同步电抗;

X'd，X″d——d 轴瞬变、超瞬变电抗;

Xq，X″q——q 轴同步、超瞬变电抗;

T'do——d轴开路暂态时间常数;

T″do，T″qo——d、q 轴开路超瞬变时间常数;

H——电机惯性时间常数;

ω——电机电角速度;

Tm——输入机械转矩;

δ——q轴领先同步旋转坐标系实轴x的角度。

需要注意的是，式(1)～式(7)表示的模型并不是一个严格的5阶模型，为了公式的简化和便于分析，在公式的推导过程中，对式(3)、式(4)做了一些近似处理，这样也便于后面的进一步推导和仿真模型的建立。

本文中数字仿真采用MATLAB/Simulink的基本模块实现，考虑到MATLAB求解状态空间表达式的强大运算能力，将式(1)～式(5)变形如下:

其中式(8)为状态方程，式(9)为输出方程，状态量为 x=［E'qE″qE″d］T，输入变量为 u=［Efidiq］T，输出量为 y= ［uduq］T。由式(8)、式(9)表示的状态空间方程和式(6)、式(7)一起，构成了同步发电机的5阶数学模型。

下面推导以［Efuduq］T作为输入量，［idiq］T作为输出量的同步发电机5阶模型的状态空间表达式。

式(8)、式(9)可记为

由式(9)有:

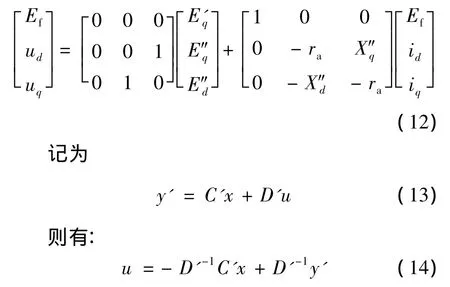
代入式(10)有:

由式(14)有:

由式(15)有:

式(16)、式(17)即为以 [Efuduq]T作为输入量，[idiq]T作为输出量的同步发电机5阶模型的电路方程。

有了上述两种不同形式的电机模型5阶方程，可以满足小型系统中大多数仿真问题的需要。

2 仿真模型的建立

表1为本次仿真所选的电机技术参数。

表1 同步发电机电抗和时间常数

根据式(8)、式(9)计算得到各系数矩阵如下:

通过以上系统矩阵，构建同步发电机的电路计算模块。

出于仿真的需要，同步发电机的仿真模型除了根据状态空间表达式建立电路计算模块和根据运动方程建立的转矩计算模块之外，还需要增加一些辅助模块，以方便与外部网络进行连接和控制。同时，在同步发电机模型内增加励磁系统模块，目的是变负载仿真时维持发电机端电压恒定，以及多机并联仿真时调节无功功率的输出。文献［7］介绍了同步发电机调压系统的几种数学模型，文献［8］则根据传递函数模型对励磁系统进行了建模与仿真。本文采用的励磁系统基于PI调节器，并使用限幅模块以限制励磁电压的幅值。图1为在Simulink中根据式(8)、式(9)所构建的同步发电机模型的内部结构图。

图1 同步发电机的Simulink模型

同步发电机仿真模型外部端口如图2所示。发电机输入共四个量，从上到下分别是转速、控制信号、负载电流和励磁电压增量;输出有三个量，从上到下分别是电机定子端电压、定子电流和电机转矩。控制信号端口输入布尔量0和1可控制发电机的运行和断开，励磁电压增量端口用于并网和多机并联仿真时调节发电机模型输出的无功功率。

图2 发电机仿真模型外部端口

3 仿真试验

小型系统中同步发电机所涉及的仿真内容非常多，主要包括短路故障仿真、突加突卸负载仿真、多机并联仿真等。限于篇幅，本文只对单机运行加载和减载的过程进行仿真。

图3和图4为同步发电机单机起动运行到断开过程的仿真结果。发电机接近同步转速后，约0.5 s时开始加励磁电压，发电机励磁磁场逐渐建立，空载端电压逐渐升高到额定电压。当励磁系统控制端电压达到额定电压以后，1.5 s时接入80%额定负载(阻感性)，电压跌落，在励磁系统的调节下又逐渐恢复到额定值，此时电流为额定电流的0.8倍。2.5 s时断开负载，电流变为0，电压经调整后仍保持额定电压。

从图中不难看出，励磁绕组磁场建立的过程持续了几百毫秒，相比之下，接入负载时定子端电压跌落的时间则短得多。因此，忽略定子绕组的暂态过程，对百毫秒级以上的动态过程以及整个系统的仿真结果影响非常有限。

图5和图6为仿真同步发电机运行过程中突加突卸负载时定子电压、电流波形。3 s时同步发电机稳定运行，所带负载为额定负载的40%，4 s时突加1倍负载，1 s后负载减回40%。

从电压、电流波形变化趋势看，突加突卸负载的仿真结果同样与实际情况相吻合。

图3 单机起动运行到断开过程的定子端电压

图4 单机起动运行到断开过程的输出电流波形

图5 突加突卸负载过程的定子端电压

图6 突加突卸负载过程的输出电流

4 结语

本文根据小型独立系统仿真的特点，选择5阶数学模型构建同步发电机的仿真模型。这样做的优点是能根据实际的仿真情况，灵活改变仿真模型的输入输出量，同时保证模型的仿真精度。最后通过在仿真软件中对所建模型进行单机运行仿真，并取得预期的仿真结果，验证了模型的正确性和实用性。限于篇幅，对小型系统中同步发电机单机并网与多机并联等典型问题动态特性的进一步仿真将另文讨论。

［1］贺益康.交流电机的计算机仿真［M］.北京:科学出版社，1990.

［2］Liu Xue Zhi，Liu Di Chen，Huang Yong.Simulation of three-phase short-circuit at the terminals of synchronous machine［J］.Electrical Machines and Systems，2008(12):115-117.

［3］李岩，苏学军.同步电机动态运行特性仿真研究［J］.电机技术，2001(4):3-5.

［4］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［5］韩富春，闫根弟.暂态稳定数字仿真中发电机数学模型的研究［J］.太原理工大学学报，2005(1):75-78.

［6］申健，金钧.电力系统仿真分析中几种同步发电机数学模型的比选［J］.电气技术，2007(9):48-51.

［7］黄曼磊，李殿璞.船舶电站同步发电机调压系统的数学模型［J］.哈尔滨工程大学学报，2004(6):305-308.

［8］罗国云，严东超，张海荣.同步发电机励磁调节系统建模与仿真［J］.微特电机，2003(3):19-20.