邻域灰度与空间特征相结合的互信息配准方法研究

魏玉兰 颜云辉 李 兵 张 尧 李 骏

东北大学,沈阳,110004

0 引言

图像配准就是对取自不同时间、不同传感器或者不同视角、同一场景的两幅或者多幅图像匹配的过程,它被广泛地应用于遥感图像、医学影像、三维重构、机器视觉等诸多领域中[1]。图像配准按照配准过程可分为基于特征的图像配准和基于灰度的图像配准。一般说来,基于特征的方法具有需要人工干预、特征点获取比较困难等缺点。除此之外,通过图像分割等技术来确定图像的特征也存在较大的问题。因为图像分割的精确度和评价标准还没有得到很好的解决,加上操作者的水平和主观因素的影响,给配准结果带来很大的不确定性。基于灰度的配准方法是直接利用整幅图像的灰度度量两幅图像之间的相似性,然后,采用搜索方法寻找相似性度量的最大值点或最小值点,从而确定两幅图像之间的变换模型参数的方法。常见的算法有最大互信息法、相关法、条件熵法、联合熵法等。基于灰度的配准方法只对图像的灰度进行处理,可以避免主观因素的影响,配准结果只信赖于配准方法本身,同时可以避免因图像分割给配准带来的额外误差,并能实现完全自动的配准。最大互信息法几乎可以用于任何不同模态图像的配准,它是一种自动的、基于像素灰度的方法,不需要选择标志点或提取图像特征,不需要假设图像中各像素的灰度值之间存在某种线性关系,因而得到了广泛应用,成为当前图像配准领域的研究热点。但基于灰度的配准方法也存在一些缺点,如计算量大、配准时间长、对噪声敏感、忽略了图像的空间相关信息等。

本文提出的方法旨在解决互信息对噪声敏感及忽略了图像的空间信息会引起配准误差两方面的问题。因为互信息量对噪声、采样点个数比较敏感,当图像空间分辨率比较低,有噪声影响和图像部分缺损时容易出现误配,所以很多学者提出了改进方法。Studholme等[2]提出的归一化的互信息方法解决了对图像间覆盖程度较敏感的问题,但该方法仍然忽略了图像的空间与方向信息。Pluim等[3]提出了将互信息量与图像梯度相结合的方法,在一般情况下能够达到较好的效果,但由于图像梯度本身对噪声十分敏感,当图像中存在一定的噪声时,该方法的配准成功率就变得比较低。Rueckert等[4]提出了一种扩展的互信息框架,将二阶熵形式的互信息成功地应用到了非刚体的配准中,由于计算二阶联合熵时要用到四维联合直方图,因此运算量非常大。本文考虑到像素点与其邻域内不同方向上的点的关系,将空间信息引入到配准的过程中,从而克服了前面提到的问题,消除了噪声对图像配准效果的影响,达到了较好的配准效果。

1 基于互信息的图像配准方法

互信息技术是最近几年提出的解决多模态图像配准的一种有效方法[5-7]。互信息是信息统计学中的一个重要概念,用来描述两个系统之间的统计相关性。互信息理论中的一个重要概念是熵[8-9],是由Shannon最早提出的。熵是一个统计量,它衡量了变量的任意性。一个随机变量,它的任意性越大,熵就越大。两个随机变量之间的相关熵就称为互信息。互信息I(U,V)是对随机变量U和V之间统计依存程度的信息度量,主要描述两组图像信息间相关的程度。对同一位置处的两组图像而言,对应的像素对之间的灰度在统计学上并非独立,而是相关的,这是互信息匹配的基础。互信息具有对称性和非负性,当且仅当U和V独立时,互信息为零,也就是说：U和V独立,互信息为零,同时U和V是不相关的,相关系数也为零;但U 和V不相关,相关系数为零时,并不代表U和V是独立的,可能两者的灰度存在非线性联系,这时互信息不会是零,这就是互信息相对于其他测度的优势。对于两幅待配准的图像,如图1所示,圆代表了图像的熵,两圆合并区域为联合熵,重叠部分就为互信息。图中明确地给出了三者之间的关系,互信息综合了图像的熵、联合熵,其形式为两者的差,即

式中,H(A)和H(B)分别为图像A和图像B的熵;H(A,B)为图像 A、B的联合熵。

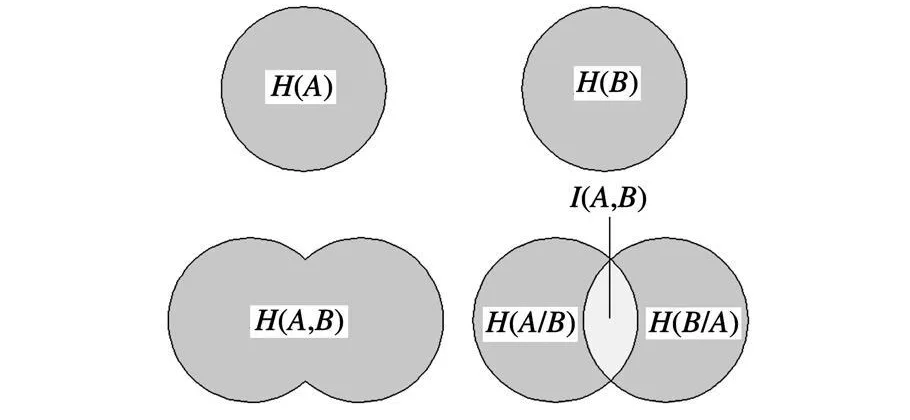
图1 互信息示意图

互信息随着两幅图像相匹配区域的大小而变化。相匹配的区域越大,则它们的联合熵越小、互信息越大。当两幅图像达到最佳匹配时,它们对应像素的灰度互信息达到最大。也就是说,可以通过寻找两幅图像的最大互信息值来判断两幅图像是否配准。

图像A的熵可表示为

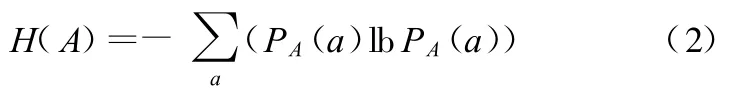
式中,a为图像A像素的灰度值;PA(a)为灰度值出现的概率。

由熵的定义可知,熵的大小并不依赖于灰度本身,而只依赖于这些灰度出现的概率。显然平移、旋转等刚性变换只是改变了像素点的空间位置,并没有改变像素点灰度值的大小,也就没有改变灰度值出现的概率,从而对熵并没有影响。

图像A、B的联合熵可由下式计算得出：

式中,b为图像B像素的灰度值;PA,B(a,b)为图像 A、B的联合概率密度。

将式(2)和式(3)代入到式(1)中可得图像A、B的互信息为

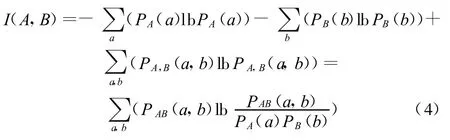
基于互信息的配准方法可视为一个寻优过程,其基本思想是通过寻找一组空间变换参数,使得其中一幅图像经过空间变换后与另一幅图像达到空间一致,此时互信息值达到最大,数学表达式为

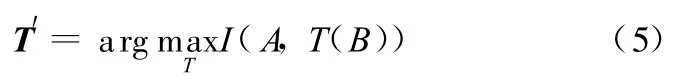
式(5)表示首先对浮动图像B按T进行空间变换,得到变换后图像T(B),然后计算参考图像A与变换后图像T(B)之间的互信息值I,通过优化算法寻找变换矩阵T′使得此时的互信息值I(A,T(B))达到最大,即实现配准图像A和B的目的。

2 邻域灰度与空间特征相结合的互信息配准方法

目前己有不少文献表明互信息配准法存在配准鲁棒性问题,容易导致误配,其原因主要是：①待配准图像由于部分图像缺失或发生形变,导致包含的有效信息大大减少;②算法运行中往往通过少采样来减小数据量,这样必然降低图像空间分辨率和减少图像所包含的信息量;③当图像噪声较大时,图像间的相关性较弱,寻优过程落入局部最优而非全局最优[10]。

利用本文提出的方法计算互信息时,参与运算的不再是图像中每个像素的灰度值,而是运用邻域内像素之间的几何距离关系及灰度变化关系来修正原中心像素的灰度值。采用离中心像素几何距离近且灰度值相似的像素的加权平均值代替原中心像素灰度值,这样既利用了像素的灰度变化信息又利用了图像像素之间的空间信息,可有效避免噪声对配准结果的影响。

结合邻域灰度与空间特征的各信息熵计算公式如下：

根据式(6)～式(8)可得出结合邻域灰度与空间特征的互信息(region intensity and spatial mutual information,RISMI)为

式中,a′和b′为图像A、B结合了邻域信息以后的灰度值;PA′(a′)与 PB′(b′)是图像 A、B 中结合邻域信息后灰度值为a′、b′的像素出现的频数;wa、wb分别为图像A和B在邻域内各像素的权值,PA′B′(a′,b′)为图像 A′、B′的联合概率密度。

wa、wb分别由两部分组成,一部分为邻域内像素与中心点像素距离关系权值w[7]d,另一部分为邻域内像素与中心点像素间灰度差值所决定的权值 wa r 和 wb r。wa r、wb r、wd、wa、wb 的计算方程分别为

式中,i、j分别为中心像素与邻域像素之间的水平距离及垂直距离;d为邻域内像素与中心像素之间的距离,且为d=1时的像素总个数;n2为时的像素总个数。

在式(14)中,如果d选取过大将导致在计算a′和b′时过多地引入灰度值和与其无联系的像素,不仅影响了配准精度,增加了计算量,还影响了配准速度。由于相邻像素灰度值之间存在着联系,离中心像素越近的像素其灰度值与中心像素的联系越紧密,因此在计算时将邻域内各像素与中心像素之间的距离大小作为权系数w d的设定依据,离中心像素距离越近权值越大。

权值war和wbr分别表达图像A和B在邻域内各像素与中心像素的灰度变化关系。当中心像素位于背景区域时,中心像素与邻域内各像素灰度接近,权值较大,此时wa r和wb r对原中心像素灰度值影响较小;当中心像素位于背景与目标之间的边缘上时,和值的变化直接反应了图像A和B的边缘灰度变化。

邻域内像素之间的空间距离权值wd和灰度变化权值w a r和w b r的引入,使得在配准过程中,不仅考虑了两副图像之间的灰度关系,同时兼顾了空间位置关系及灰度变化特征对互信息的影响,从而克服了因噪声及图像缺失对配准结果的影响,大大提高了互信息配准的鲁棒性。

3 实验结果及分析

3.1 配准结果分析

为了验证本文方法的有效性,对采集到的带钢表面明暗域缺陷图像进行配准实验,配准图片如图2所示。其中,图2a为采用面阵CCD,光源与CCD成35°时采集到的明域缺陷图像,图2b为光源与CCD成10°时采集到的暗域缺陷图像。两副图像来源于同一个CCD,采集同一位置处的带钢表面缺陷,唯一不同的是光源与CCD的角度不同,因此,此时的两副图像是完全配准的。为了证明本文提出方法有优越性,将明域图像作为参考图像,即空间位置不变,首先对暗域图像进行某一参数的变换(旋转10°,水平和垂直方向各平移5个像素),然后将其与明域图像进行配准。

图2 配准图像

分别采用文献[3]中提出的归一化互信息(normal mutual information,NMI)及文献[8]中提出的互信息与梯度相结合的梯度互信息(gradient mutual information,GMI)和文中的RISMI测度进行配准,配准后的结果如表1所示。

表1 NMI、GMI与 RISMI配准结果对比

参考值是指明域缺陷图像的空间变换参数,从表1可以看出,三者的配准结果都非常接近于精确值,但以RISMI和GMI为相似性测度的配准方法要更加精确一些,这是因为RISMI包含了邻域内各像素的空间位置信息与灰度变化信息的作用,GMI充分考虑了梯度对配准结果的影响。

3.2 对高斯噪声鲁棒性分析

为了验证本文提出方法对高斯噪声的鲁棒性,在图2原始图像的基础上,分别加上均值为0、方差为0.01的高斯噪声,如图3所示。

图3 加高斯噪声配准图像

分别采用 NMI、GMI和 RISMI方法进行配准,配准数据如表2所示。

表2 NMI、GMI与RISMI配准结果对比(加噪声后)

从表2中的数据我们可以看出,当图像中含有高斯噪声时,经过改进的结合邻域灰度与空间特征的互信息配准方法配准的结果更接近最优值。GMI的配准结果精度明显下降,这主要是因为梯度对噪声比较敏感,噪声越大配准结果越不准确,因此该方法对噪声的鲁棒性较低。传统的NMI方法,由于噪声的存在,使得配准结果陷入局部最优,造成误配准。实验结果充分证明,改进的RISMI测试具有更高的抗高斯噪声干扰性,且配准精度更高。

4 结束语

基于归一化互信息的配准方法适应多模态图像之间的自动配准,具有无需先验知识、配准精度高等优点;但其主要问题是当配准图像存在高斯噪声时,容易陷入局部最优,造成误配准。通过将互信息与空间邻域内各像素的空间位置信息与灰度变化信息相结合,不仅利用了图像的灰度信息,还充分利用了图像的空间信息。实验结果表明该方法比传统的互信息方法具有更好的鲁棒性,在图像含有高斯噪声的情况下,仍可得到比较理想的配准效果。

[1] 陈显毅.图像配准技术及其MATLAB编程实现[M].北京：电子工业出版社,2009.

[2] Studholme C,Hill D L G,Hawkes D J.An Overlap Invariant Entropy Measure of 3D Medical Image A-lignment[J].Pattern Recognition,1999,32(1)：71-86.

[3] Pluim J PW,Maintz JB A,Viergever M A.Mutual Information Matching in Mult-iresolution Contexts[J].Image and Vision Computing,2001,19(1/2)：45-50.

[4] Rueckert D,Clarkson M J,Hill D L G,et al.Nonrigid Registration Using Higher-order Mutual Information[C]//Proc.SPIE Medical Imaging 2000：Image Processing.San Diego,2000：438-447.

[5] Wachowiakm P,Smolikova R,Peters T M.Multiresolution Biomedical Image Registration Using Generalized Information Measures[C]//Proc.MICCAI 2003.New York,2003：846-853.

[6] Maes F,Vandermeulen D,Suetens P.Medical ImageRegistration Using Mutual Information[J].Proceedings of the IEEE,2003,91(10)：1699-1721.

[7] Josien P,Antoine J,Max V.Image Registration by Maximization of Combined Mutual Information and Gradient Information[J].IEEE Trans.on M edical Image,2000,19(8)：809-814.

[8] 叶中行.信息论[M].北京：高等教育出版社,2003.

[9] 毛璐璐,徐刚锋,陈显波.基于互信息与梯度融合的多源图像匹配技术研究[J].红外技术,2009,31(9)：532-536.

[10] 刘青芳,李月娥.基于改进的互信息结合边缘互方差的医学图像配准方法研究[J].测试技术学报,2009,23(6)：535-539.