V带疲劳寿命最长的全局优化设计

张少军 万 中 刘光连

中南大学,长沙,410083

0 引言

V带传动具有结构简单、运行平稳、低噪声、能缓和载荷冲击、传递功率较大、能实现过载保护、生产成本低以及制造和安装容易等一系列优点,所以广泛应用于各类机械中[1-2]。对V带工作能力的考虑主要包括两个方面,即V带传动能力和V带的寿命。二者密切相关且相互矛盾,若提高V带的传动能力,则V带的寿命就会降低;反之亦然[3]。从V带传动实际使用情况来看,对于长期连续运转的V带,寿命是主要要求;而间歇工作的V带,传动能力则上升为主要要求。如何根据所需传递功率、主动轮转速等条件使设计出的V带传动系统中V带疲劳寿命最长,这对于节约资源、降低成本、提高系统可靠性具有积极意义。

为了实现V带传动的优化设计,国内外学者进行了诸多研究。文献[4-6]对已有理论和方法作了较系统和全面的阐述。此外,还有一些软件公司开发了专门的V带设计软件(如Ciclo VBelt)。最近的研究成果可参看文献[7-8]。文献[7]用改进的遗传算法对带传动多目标进行了优化,文献[8]对V带轮的疲劳寿命进行了优化。不过,在已有的文献中,尚未见到关于V带疲劳寿命最长的全局优化设计问题的讨论,而是较多关注于对V带传动能力[9]、带轮体积[10]等的优化,或仅限于对V带疲劳寿命优化的原理性探讨[11-12],或者对所建立的优化模型采用一些经典的局部优化算法(如罚函数方法)求解。本文在建立V带疲劳寿命最长优化设计模型的基础上,通过深入分析目标函数和约束条件的性质,在给定的设计条件下提出全局优化方法。

1 V带疲劳寿命最长优化模型

假设V带型号确定,小带轮(即主动轮)转速n1(r/min)和传动比i给定,要通过选取设计变量V带节线长(简称带长)L(mm)、小带轮直径 d1(mm)和单根V带所要传递的功率P(k W)来使得V带疲劳寿命T(h)最长。

由实验可知,V带最大应力δmax与它的总循环次数N有如下关系：

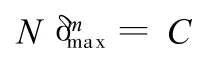
式中,C为实验常数,由传动带的材质、结构和尺寸决定;m为曲线指数(一般为6～11)[11],当V带型号确定且 N可能的变化范围不是很大的情况下,可近似地视m为一恒定值(如 N为108～109时,m取11.1)[13]。

由上式出发,根据V带传动的应力分析[14],可推导出特定参数情况下单根V带在两轮间传动时所能传递的最大功率P0为

式中,v为带速,m/s;Eb为V带弯曲弹性模量,MPa;y0为V带外层至中性层距离,mm;Ki为传动比系数;ρl为V带线质量,kg/m;A为V带横截面积,mm2;μV为V带与带轮槽间的当量摩擦因数;α为小带轮包角,rad。

假设单根V带所要传递的功率P在其所能传递的极限功率范围内,由于V带疲劳寿命随传动带的初张力F 0增加而显著降低[15-16],为保证所需传递的功率又不出现打滑现象,且V带疲劳寿命T最长,这时需将初张力调整到刚好满足所需传递功率要求,也即此时单根V带所要传递的功率P就等于它所能传递的最大功率P 0。

设设计变量 x=(x1,x 2,x3)T=

根据实际生产工艺和工程要求,V带传动设计必须考虑基本约束条件如下：

(1)中心距设计约束：

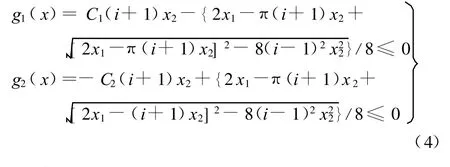
(2)V带的带速限制：

(3)单根V带传递功率限制：

(4)小带轮直径设计约束：

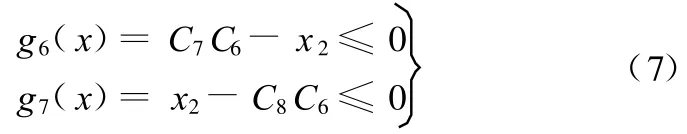
(5)V带节线长设计约束：

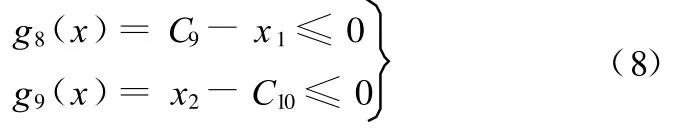
(6)小带轮包角设计约束：

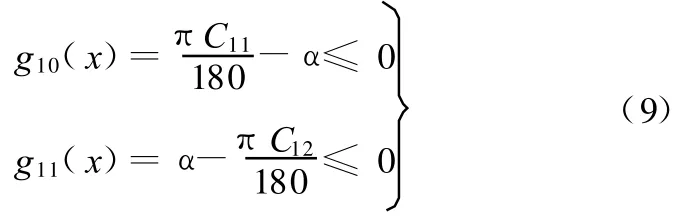
其中,C1～C12为约束条件中的常系数,具体数值见表1。

表1 V带优化模型中的常系数列表

因此,V带疲劳寿命最长优化设计模型为

以往的V带传动优化设计中,常常利用一些经典的算法(如罚函数方法)[17]求解式(10)。其主要缺陷在于：①没有更深入地分析该问题目标函数的性质和可行域的结构,因而采用的算法未必是计算效率最高的;②如果式(10)不是凸规划问题,采用任何经典的优化算法都不能从理论上保证所求得的解是该问题的全局最优解。本文的主要工作就是要在深入分析式(10)结构性质的基础上,提出针对该问题的高效算法。

2 目标函数的性质和可行域的结构

为了设计最有效的求解上述优化问题(式(10))的算法,首先证明一下目标函数的一些结论。

定理1 目标函数T(x 1,x2,x3)关于第一个变量x1在区间(0,+∞)内单调递增,关于第三个变量x3在区间(0,+∞)内单调递减。

证明：目标函数T(x1,x2,x3)关于第三个变量x3在区间(0,+∞)内单调递减是显然的。由式(3)不难证明α关于变量x 1在区间(0,+∞)内的单调递增。由式(2)也可证明目标函数T是关于α在区间(0,+∞)内的单调递增函数。根据复合函数及其导数的性质,容易证明目标函数T关于变量x 1在区间(0,+∞)内单调递增,因此定理的结论成立。

设单根V带所要传递的功率不小于Pmin。由于x 3在优化模型中相对独立,且T关于变量x 3在(0,+∞)内单调递减,因此可首先取定 x3=P min,这样模型中就只剩下 x1、x2两个待设计变量。

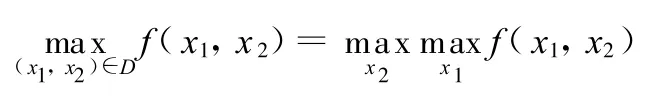
证明：首先

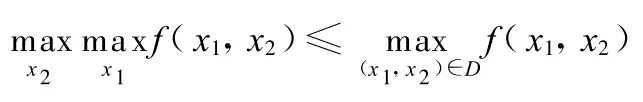
是显然的,我们只要证明

成立。

对任意给定的x2,令

因为D是单连通的有界闭集,所以I(x2)是有界闭区间,记此区间的右端点为r(x2)。

因为f是D内的连续函数,且关于x1单调递增,所以对任意点(x 1,x2)∈D,有

又记

则集合P x2(D)是D在x 2轴上的投影。因为D是单连通有界闭集,所以Px2(D)是 x2轴上的有界闭区间。

因为 f是D内的连续函数,所以 h是有界闭集P x2(D)上的连续函数,且存在最大值点x*2。

由式(11)和 h的定义知,对任意点(x1,x2)∈D,有

所以

尽管优化模型(式(10))中的目标函数在区域R2

+内无界,但定理2对我们在下节提出求解式(10)的最有效的全局优化方法有很多帮助,因为后面我们将证明该问题的可行域是有界闭凸集。因此,根据定理2,我们能够提出优化模型(式(10))的全局最优解满足的条件。下面证明目标函数在一般情况下不是凹函数,从而原问题不能用凸规划方法求解。因此可以肯定,以往研究工作中采用经典的局部优化算法不能从理论上保证求得的解是原问题的最优解。

定理3 目标函数T不是凹函数。

证明：事实上,若取定B1=711.017,B2=10.507,B3=94.157,B4=0.55×10-6,i=3.65,m=11,则当 x1=2000、x2=154时,T的 Hesstan阵

是不定矩阵。因此,目标函数一定不是凹函数(任何点处Hessian阵为负定矩阵)。

接下来,我们研究优化问题(式(10))的可行域结构。为此,我们把约束条件式(4)～式(9)作如下简化：

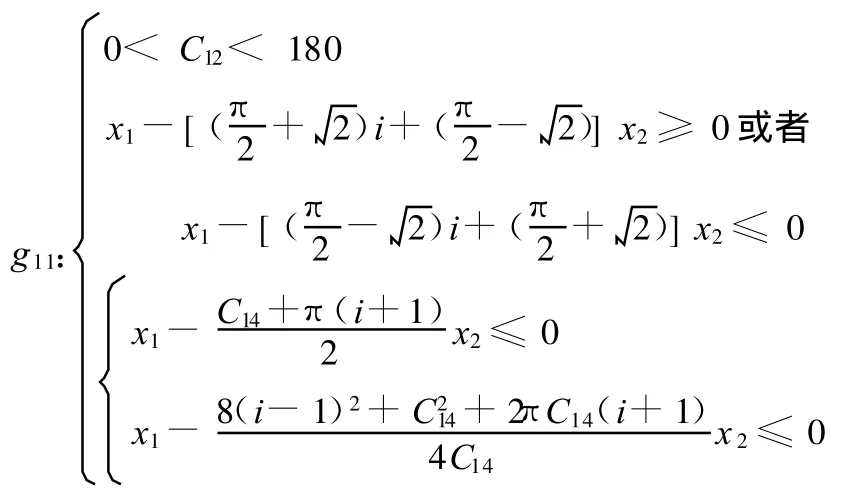
或取C12=180,此时由g1约束式和i≥1可知原g11约束恒成立。

将 g3、g4 、g6、g7 约束式合并为

将g8、g9约束合并为

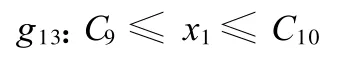
以上 g1、g2、g5 、g10、g11、g12 、g13 构成了总的约束条件,它们均为线性约束,因此我们可得如下结论：

定理4 优化模型的可行域Ix={(x1,x2)∈R2

+|(x1,x2)满足条件式(4)～式(9)}是有界闭凸集(此时x3取为定值P min)。

3 全局优化算法

基于定理1、定理2和定理4,我们提出如下计算优化模型全局最优解的高效算法(我们称之为最优值线段算法)：

(1)把式(10)(此时x3取为定值Pmin)中每一个约束条件归为如下三类之一：①x1≤kx 2,k＞0;②x 1≥kx 2,k＞0;③a≤x1≤b,c≤x2≤d,a、b、c、d均为大于零的常数。

(2)取k1=min{k|k是第 ①类约束的斜率},k2=max{k|k是第②类约束的斜率}。一般地,k1≥k2。设直线x 1=k1 x2与直线x1=a交点的纵坐标为ea,与 x1=b交点的纵坐标为eb。直线x1=k2x2与直线x1=α交点的纵坐标为ga,与x1=b交点的纵坐标为g b。则

①当ea＞d时,问题无解;②当ea≤d且eb≥d时,可直接得到该问题的全局最优解x*=(x*1,x*2)=(k1 d,d);③当eb＜d且g b≥c时,则在直线段x 1=b,(max{c,eb}≤x 2≤min{d,gb})上寻找最优解,此时将x1=b代入到目标函数,则原优化问题可归结为一元连续可微函数在有界闭区间上的全局优化问题,再利用有效的全局优化方法,如覆盖法[18],就能得到原问题的全局最优解;④当gb＜c时,该问题无解。

4 设计实例

试以V带疲劳寿命最长为目标设计一V带传动系统。其中主动轮转速n1=1460r/min,传动比i=3.65,用普通B型V带传动,其单根V带传递功率P不小于P min=3.50k W。

查表[19]得普通 B型 V带参数：ρl≈0.17kg/m,A=142.96mm2,y0=4.1212mm。Eb=55.7MPa,K i=1.1373,μV=0.51,C ≈1.8099×1014。优化模型中各系数值如表 2所示。

表2 设计实例的模型系数值列表

首先选定 x3=3.50kW。经计算得：B2=24.4824,B3=30.8592,B4=0.5312×10-6。

通过整理各约束条件得到总的可行域Ix为

图1 实例中可行域Ix的图形

此优化问题可行域的特点符合最优值线段算法(2)中的情形 ②。由最优值线段算法可知,T(x)的全局最大值解必然就是图1中的点C,即全局最优解x*=(4018.322,154,3.50)T。设此问题中m取值为11.0,则V带疲劳寿命最长的全局最优值 Tmax≈61923h。

在已有的文献中,尚未见到关于V带疲劳寿命最长优化设计问题的具体研究,所以无从比较。但在文献[20]中计算得到的普通B型V带在额定功率工作时的预期疲劳寿命约为24 000h,远低于本实例中得到的B型V带疲劳寿命最长的全局最优值。这也反映了本文优化模型和优化方法的有效性。

工程实际中由于工作空间或机械整体尺寸的限制,有时还要求中心距a≤a max,其中a max为一常数,这相当于在原模型中增加约束条件：

即

以上为一线性约束和非线性约束的组合。当曲线

为可行域Ix沿坐标x 1增大方向一侧的全部或部分边界时,可行域就不一定是凸集。但此时并不妨碍上述最优值线段算法的使用。若可行域最右侧边界全部由该二次曲线组成,则可按最优值线段算法(2)中情形 ②的处理方法来计算最优解,最优解为

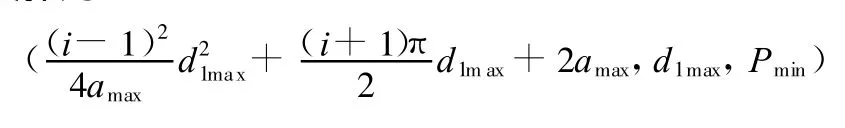
其中,d 1max为小带轮直径在可行域范围内能取到的最大值。若可行域最右侧边界只是一部分由该二次曲线组成,则可按(2)中的情形 ③来计算。

5 结束语

本文建立了以V带疲劳寿命最长为目标的优化设计模型。深入研究了该模型中目标函数的凸性、单调性等特性,证明了其可行域是有界闭凸集。以此为基础提出了求解该模型的一种全局优化解法——最优值线段算法。最后的实例说明了该模型和全局优化方法的有效性和实用性。

[1] Gerbert B G.Some Notes on V-belt Drives[J].ASME Journal of Mechanical Design,1981,103(1)：8-18.

[2] Shieh C J,Chen W H.Effect of Angular Speed on Behavior of a V-belt Drive System[J].International Journal of Mechanical Sciences,2002,44(9)：1879-1892.

[3] 刘雍德.V带传动设计方法探讨[J].湖北汽车工业学院学报,1997(3)：1-4.

[4] Sharma CS,Purohit K.Design of Machine Elements[M].New Delhi：Prentice Hall of India,2003.

[5] Hamrock B J,Schmid S R,Jacobson B O.Fundamentals of Machine Elements[M].2nd Edition.New York：McGraw-Hill Science,2004.

[6] Bhandari V B.Design of Machine Elements[M].New Delhi：Tata McGraw Hill Publishing,2007.

[7] 宋俐,魏锋涛,刘伟.基于改进遗传算法的带传动多目标模糊优化设计[J].机械传动,2006,30(5)：28-30.

[8] Shim H J,Kim J K.Cause of Failure and Optimization of a V-belt Pulley Considering Fatigue Life Uncertainty in Automotive Applications[J].Engineering Failure Analysis,2009,16(6)：1955-1963.

[9] 龚小平,仝崇楼,刘永强,等.V带传动可靠性优化设计[J].现代机械,2002(1)：50-52.

[10] 严寒冰,原思聪,季文祥.基于遗传算法及MATLAB的 V带传动优化设计[J].机械,2008,35(9)：23-25.

[11] 刘金石.按工作寿命优先或最大转矩优先设计V带传动[J].四川工业学院学报,1992,11(1)：13-18.

[12] 刘雍德.不同预期寿命时V带传动额定功率计算方法的研究-对IS05292-1980计算方法的改进[J].中国机械工程,1996,7(增刊)：90-92.

[13] Spotts M F.Design of Machine Elements[M].6th Edition.Englewood Cliffs：Prentice-Hall Inc.,1985.

[14] 罗善明,余以道,郭迎福,等.带传动理论与新型带传动[M].北京：国防工业出版社,2006.

[15] 刘明洁,赵洪志,陈福恩.预测V带寿命的研究[J].农业机械学报,1994(增刊)：123-128.

[16] 刘雍德.V带的寿命计算[J].湖北汽车工业学院学报,1997(4)：1-4.

[17] 陈立周.机械优化设计方法[M].北京：冶金工业出版社,2005.

[18] 李董辉,童小娇,万中.数值最优化算法与理论[M].北京：科学出版社,2010.

[19] 机械设计手册编委会.机械设计手册：带传动和链传动[M].北京：机械工业出版社,2007.

[20] 杨宗栋,曹助家.普通V带传动的预期寿命[J].东北重型机械学院学报,1989,13(4)：56-63.