基于参数灵敏度的结构性能优化
2011-05-31李初晔王卫朝
李初晔 王卫朝 马 岩
北京航空制造工程研究所,北京,100024
0 引言
完整的结构优化设计过程包括尺寸优化、形状优化和拓扑优化几个不同阶段和层次。尺寸优化是在保证零件拓扑结构不变的前提下优化截面面积、筋板厚度等参数;形状优化是在保证设计域内的拓扑结构关系保持不变条件下,寻求最理想的边界和几何形状;拓扑优化可以在给定的设计空间中确定最优的材料分布,设计最优的零件几何、框架、加强筋布局,减少非关键区域的材料分布。连续体结构的拓扑优化包括结构边界形状的优化,通过去除材料,可在结构内部形成孔洞,拓扑优化比形状优化具有更大的自由度和开放性,而且不局限于参数形式,因此拓扑优化是高层次的优化,难度也最大,被公认为是结构优化领域最具挑战性的研究课题之一[1-2]。
从尺寸优化、形状优化到拓扑优化的这一过程提供了新产品在设计中的优化策略:①首先根据产品的工作范围确定设计空间,选择能完全覆盖零件设计区间的简单初始形状进行无参数化的拓扑优化,根据各截面的优化结果组合产生最佳的轮廓形状和孔洞分布模型;②根据拓扑优化结果修改零件初始结构,并进行参数化定义,产生拓扑优化结构;③在设计目标约束下采用尺寸优化对拓扑优化结构的设计参数进行调整;④根据尺寸优化结果对拓扑优化结构进行修改,产生最终优化结构零件。
本文采用一种基于参数灵敏度的振荡优化方法,通过令所研究结构的质量上下波动,在变形极小化目标控制下使结构参数不断发生变化,最终得到质量不变、性能更优的新结构,通过与有限元分析软件结合,这一过程很容易通过程序实现,而且能够快速收敛。
1 变量定义及有限元模型参数化
图1所示为高速铣床的横梁结构,外观的七面体结构是通过拓扑形状优化产生的,在结构细化阶段,通过参数优化确定最佳尺寸组合,使在滑板铣头组合重力和切削力作用下变形最小,并具有较高的初阶固有频率。
在方案设计阶段,横梁的外观尺寸L、W、H是根据加工零件特点初步确定的参数,H 1、W1在拓扑优化阶段可以初步确定其与 H、W的比例,H1、W1可以作为确定量,也可作为优化变量来定义。控制结构的变量分为形状变量和厚度变量,通称为结构参数。
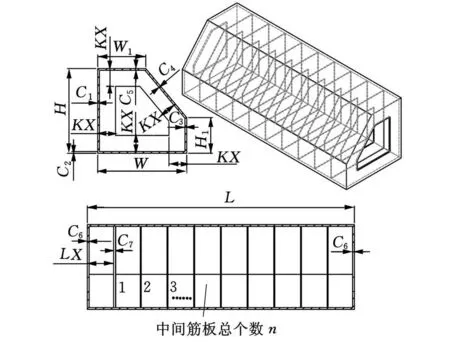
图1 横梁外观和尺寸变量
形状 变量为 H1、W1、KX 、n,厚度 变量为C1~C7。
要对结构进行性能优化,将有限元模型参数化是首要前提,因为只有带参数的结构模型才能通过参数提取,分析参数变化对目标的影响,最终达到参数优化的目的。
2 变量对结构性能的灵敏度分析
结构参数变化对质量、变形、应力和频率等性能参数皆有影响,但不同部位的形状和尺寸参数对结构性能的影响程度不同[3],通过单变量改变结构参数的大小,总结归纳对结构整体性能的重要程度,为书写方便将参数用x1~x11表示。
横梁最大变形U为结构参数的函数,U=u(x 1,x2,…,x 11),任意一组变量增量d x1,d x2,…,d x11引起的最大变形改变量d U可以表达为
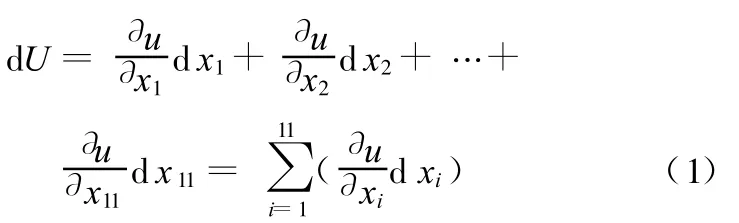
其中,∂u/∂xi为对变量xi求偏导数,称为变量 xi对函数U的灵敏度,记为ξi。如果要分析某一变量(如xk对函数U的影响),应将其余的变量固定,因此上式中除了d xk外,其他变量的增量均为0,式(1)变为

得到xk的灵敏度
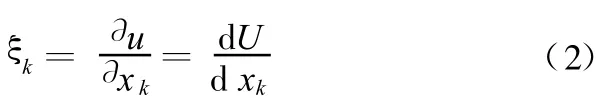
对于复杂的结构,不可能写出变形与变量之间的函数关系式,因此式(2)只有理论意义。有限元分析为我们提供了求解灵敏度的工具,比如要求解变量xk对结构变形的灵敏度,先计算出变量为xk时的变形量u1,再计算出xk增加一个单位(d xk=1)时的变形量u2,则

u1、u2可以通过两次有限元计算得到,灵敏度为“正”表明函数随该变量的增大而增大,灵敏度为“负”表明函数随该变量的增大而减小。
表1的数据反映了变量对优化目标的影响程度,通过灵敏度分析,得到以下四点结论:
(1)变量对变形的影响程度从大到小依次是:x8(-),x11(-),x4(-),x10(-),x7(-),x3(-),x9(-),x6(-),x5(-),x1(-),x2(+)。各变量后面的“-”号表示增大该变量变形减小,“+”号表示增大该变量变形增加。
(2)变量对结构应力的影响程度从大到小依次是:x11(+),x4(-),x8(-),x5(+),x7(-),x9(-),x10(+),x6(+),x2(+),x 1(+),x3(-)。各变量后面的“-”号表示增大该变量应力减小,“+”号表示增大该变量应力增加。

表1 各变量灵敏度综合一览表
(3)变量对结构质量的影响程度从大到小依次是:x11(+),x10(+),x5(+),x4(+),x7(+),x8(+),x6(+),x9(+),x3(+),x2(+),x 1(+)。各变量后面的“+”号表示增大该变量质量增加。
(4)变量对结构频率的影响程度从大到小依次是:x11(+),x10(+),x3(+),x8(-),x 7(-),x4(-),x9(+),x6(+),x5(+),x1(+),x2(+)。各变量后面的“-”号表示增大该变量频率减小,“+”号表示增大该变量频率增加。
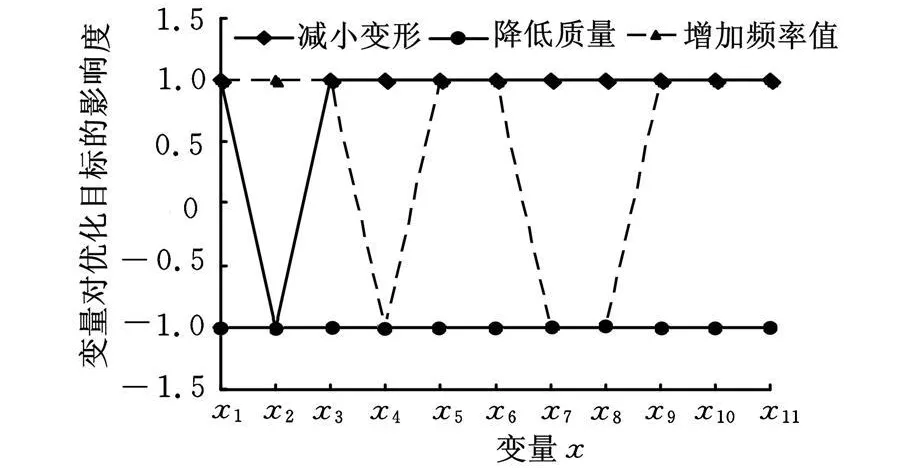
图2 变量对优化目标的影响综合
结构优化的目的是:减小变形(提高静刚度),增大固有频率(提高动刚度),减小结构质量[4-5],如果某变量的改变同时能实现上面三个目标,那么此变量在优化过程中为优先调整的变量,但从图2所示的变量对优化目标的影响综合来看,一个变量最多能使两个目标情况变好,但同时会使另一个目标变坏 ,比如增大 x1、x3、x5 、x6、x 9、x10、x11会达到减小变形、提高频率的目的,但会使质量增加;减小 x4、x 7、x8会达到提高频率、降低质量的目的,但会使变形增加,结构优化过程就要使各目标合理地达到平衡。从控制变形提高结构静刚度方面考虑,应采取的措施是:减小 x2,增加x8、x11 、x4、x 10、x7、x3、x9 、x6、x5、x1,变量的增减幅度与该变量对变形的灵敏度有关,灵敏度大的改变幅度大些,假设采用线性增减规律:

通过变换式(1)可得
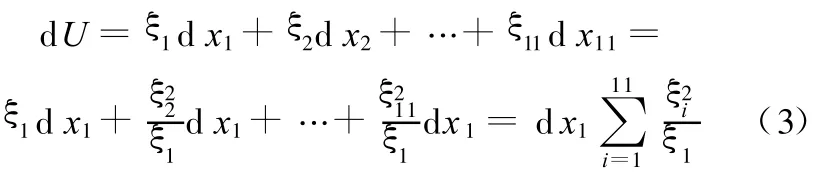
得到

因此,若已知变形控制量d U,通过上式可得到变量的允许改变量,对结构频率和质量的控制采用同样的方法进行分析。图3反映了结构变形、质量和频率变化时各变量的变化趋势。

图3 变量的变化趋势分析
3 单位质量的灵敏度分析
仅分析变量对目标的灵敏度似乎不能准确定义参数对目标函数的影响程度,因为某个变量对变形的灵敏度可能较大,但如果对质量的灵敏度同样很大,则该变量对控制变形不一定是关键变量,因为它本质上是通过增加结构质量来达到控制变形的目的的。基于这方面的考虑,定义变量xi的形质灵敏度Γi为变形灵敏度(ξi)和质量灵敏度(ζi)的比值

同理,定义变量xi的频质灵敏度Ψi为频率灵敏度λi和质量灵敏度ζi的比值:
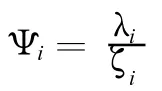
变量xi的形质灵敏度的意义是:xi代表的部分结构单位质量的改变对变形产生的影响,因此形质灵敏度反映了单位质量的材料增减对变形的影响程度,比变形灵敏度指标更能揭示变量对变形的影响。为减小结构变形,假设变量按形质灵敏度的大小采用线性增减规律:

经变换式(1)可改写为

得到

因此基于形质灵敏度又定义了一组变量增量d x1,d x2,…,d x11,表2的分析数据表明,同样使结构变形减小25%,采用形质灵敏度定义的变量增量使结构质量由2.803t增加到3.184t,增加了13.6%,采用变形灵敏度定义的变量增量使结构质量增加到3.371t,增加了20.2%,因此形质灵敏度用于结构性能优化更有效率。基于形质灵敏度和变形灵敏度,当变形减小25%时各变量的变化趋势分析图如图4所示,变量x11为横梁中间加强筋个数,为离散变量,计算时四舍五入取整数。
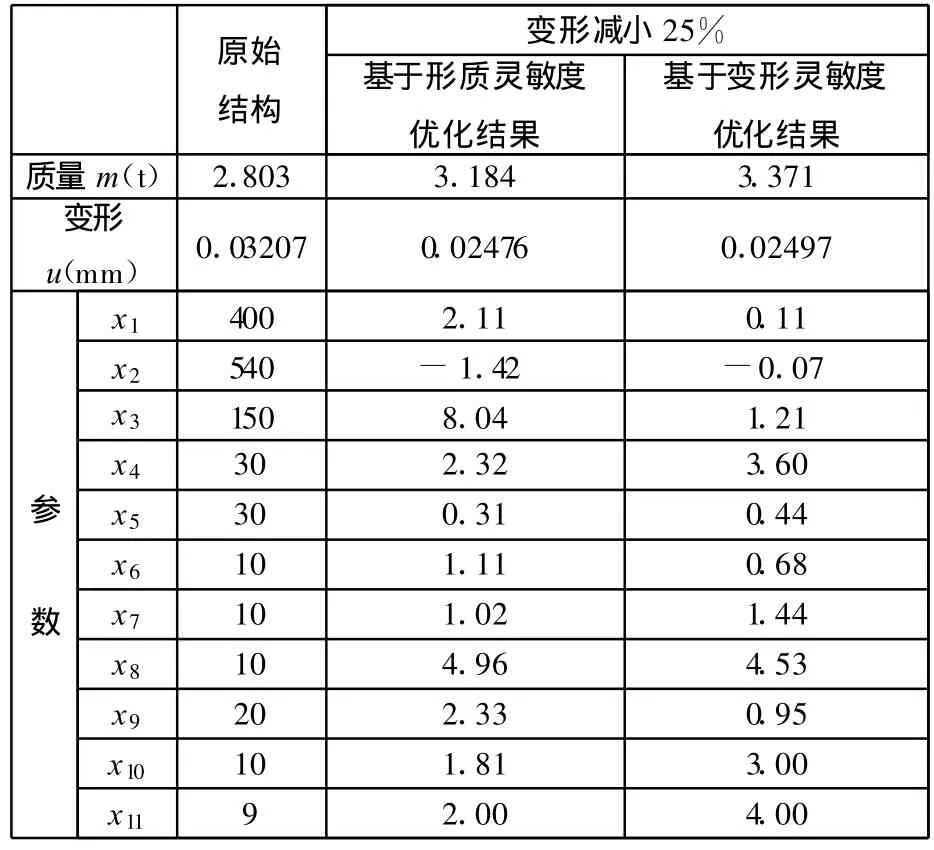
表2 采用两种灵敏度指标控制变形综合一览表
4 基于变量灵敏度的结构优化
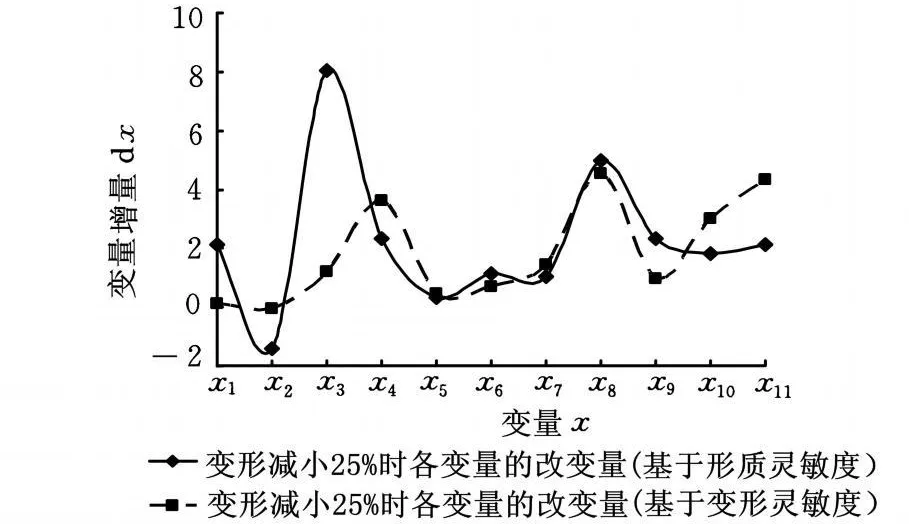
图4 两种灵敏度指标下变量的变化趋势
结构优化大多以控制变形为主,过程表现为在不增加结构质量的前提下,使变形极小化[6-7]。变量的形质灵敏度在减小质量和减小变形方面具有更高效率,对于一组初始变量x1,x2,…,xn,变形和质量的函数为

结构变量的形质灵敏度、变形灵敏度和质量灵敏度分别为 Γi、ξi、ζi,质量增量为

第一步先使质量增加d m,为限制变形的增加,变量按形质灵敏度的大小采用线性增减规律:
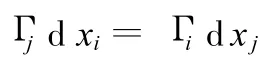
式(6)可改写为
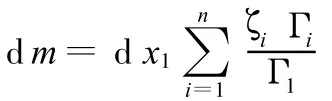
得到
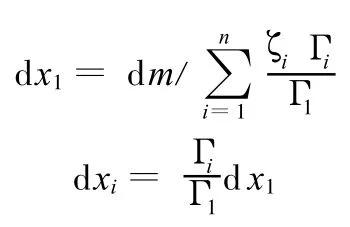
将这一步得到的增量组记为daxi:

变形增量

第二步使质量减小d m,恢复到原始水平,为限制变形的增加,变量按形质灵敏度的大小采用线性反比增减规律:
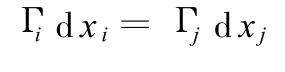
式(6)可改写为
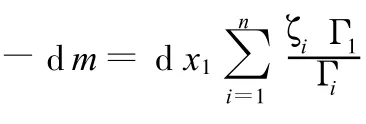
得到变量增量
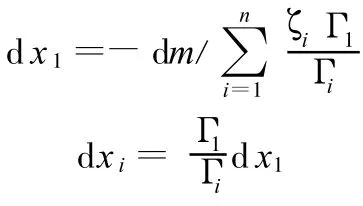
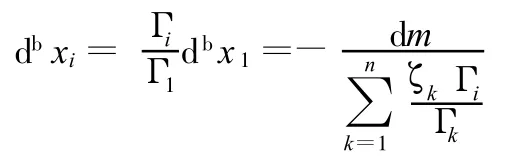
变形增量:

经过两步变换,结构质量保持不变,结构参数变为

结构变形为

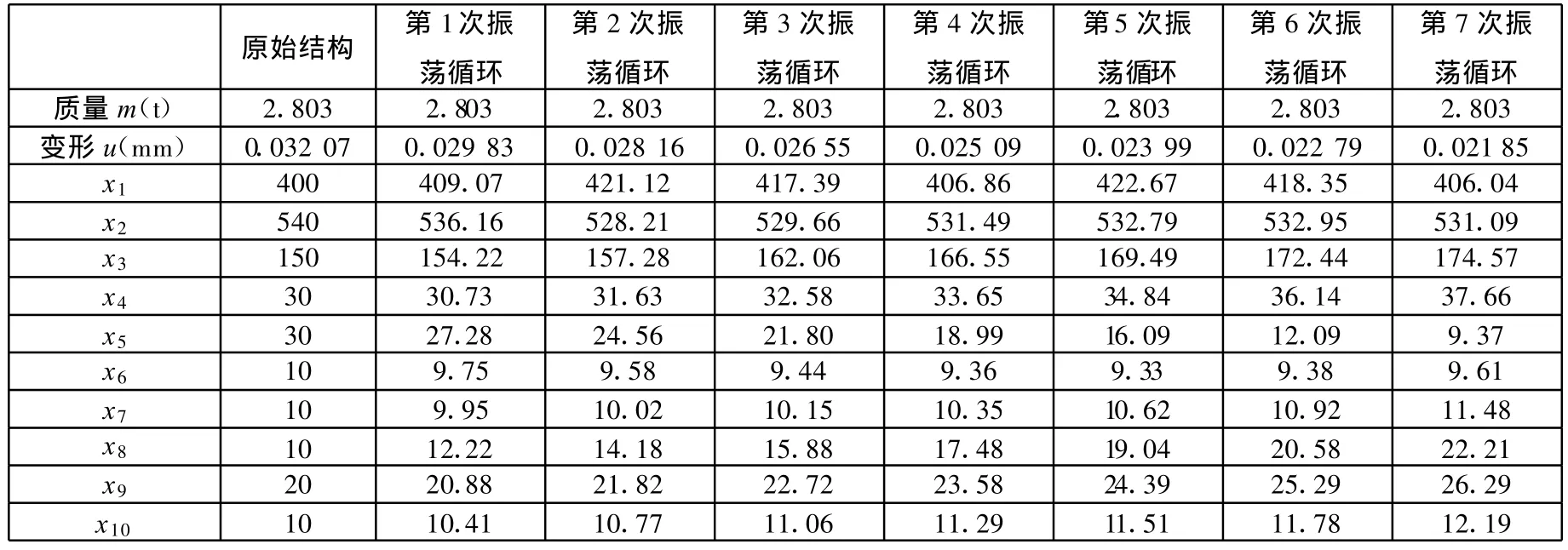
表3 7次振荡循环变量和目标信息综合一览表

图5 7次振荡循环下变量的变化趋势分析
5 基于参数灵敏度优化程序的一些验证模型
5.1 验证模型1
对于二元函数

变量的初始值x1=15,x2=-3。
在函数T保持不变的前提下,计算函数U的极值。
初始变量下函数 T的初值为
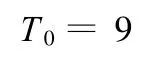
函数U的初值为

设定的函数T振荡百分比为1%,经过93次循环优化计算,得到当x1=-0.68,x2=4.84时函数U取得极小值,此时T=9,U=99.69。
5.2 验证模型2
设定变量的初始值:x1=8,x2=13,x3=22。
在S保持不变的前提下计算函数V

图6 验证模型2图例
由于结构参数随质量变化采用不同的增减规律,所以daxi+dbxi不等于0,经过参数变换产生新的结构,与原始结构相比,结构质量未变但变形已经减小。
下一个循环是将得到的新结构作为初始结构,计算产生新的形质灵敏度Γi、变形灵敏度ξi和质量灵敏度ζi指标,进行同样的两步操作,当两次循环得到的变形差小于预先设定的收敛精度时计算终止。这一优化方法通过令质量上下波动,在变形极小化目标控制下使结构参数不断发生变化,最终产生质量不变、性能更优的新结构,因此可称为振荡循环优化。表3中的数据经过7次振荡循环,横梁结构质量未发生变化,但最大变形从0.032 07mm减小到0.021 58mm,优化效果非常明显,图5所示为各变量在优化过程中的变化趋势曲线,从图5中看出,变量 x1、x3、x5变化最剧烈。的极值。函数S的初值S0=1132。函数V的初值V0=2288。
设定函数S振荡百分比为2%,经过25次循环优化计算得到,当 x1=13.62、x2=13.65、x3=13.90时,函数V取得极大值,此时S=1130,V=2584。
将面积和体积函数反过来,即在体积不变条件下求表面积的极值时,循环振荡的次数处于不确定状态,可见在体积一定的条件下表面积的极值会趋向无穷大。
5.3 验证模型3
如图7所示,从O点等角度发出n条线段,连接端点a1,a2,…,an构成封闭图形,第i个三角形的信息如下:
顶点角


图7 验证模型3图例
底边长

面积

整个封闭图形面积

整个封闭图形边长
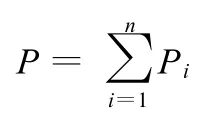
因此,我们构造了两个函数S、P。现在来计算:在保证封闭图形长度P不变的前提下,寻求面积函数S的极值条件。
假设n=10,则图形的控制变量为r1、r2、…、r10共10个,设定变量的初始值为:r 1=8,r2=8,r3=9,r4=11,r5=10,r6=9,r7=9,r8=10,r9=11,r10=9。
函数P的初值为

函数S的初值为

设定的函数P振荡百分比为0.1%,经过67次循环优化计算,当 r1=9.17、r2=9.18、r 3=9.34 、r4=9.58 、r5=9.82 、r 6=9.96 、r 7=9.94 、r8=9.78、r9=9.53、r10=9.30时函数S 取得极大值,此时 P=59.11,S=268.85。
对于外凸多边形,在边长总和给定的条件下,当ri相等时面积存在极大值:
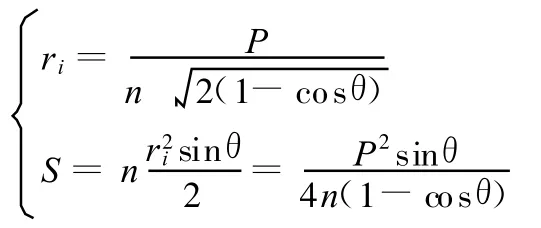
因此,r i=9.567,面积的极大值为S=269。优化解与理论解的误差为0.06%。
6 结束语
优化技术的广泛采用让设计具有了更大的创造性,对提高产品性能、创新设计思路、降低产品的价格有巨大作用,并且使CAE应用达到一个新的高度。振荡循环优化方法易于编程实现,可以应用于各种参数化有限元分析领域,笔者最早将其应用于多连杆机构的优化设计中,相信该方法是对其他优化方法的一个有益拓展和补充。基于参数灵敏度的快速优化算法,经一些数学模型和实际工程应用检验,分析结果是可信的,因此本课题从理论上是可行的。
[1] 唐文艳,顾元宪.遗传算法在结构优化中的研究进展[J].力学进展,2002,32(1):26-40.
[2] 荣见华,姜节胜,胡德文,等.基于应力及其灵敏度的结构拓扑渐进优化方法[J].力学学报,2003,35(5):584-591.
[3] 王成端,杨肃.动态优化中的灵敏度分析研究[J].计算结构力学及其应用,1991,8(1):77-83.
[4] 钱令希.工程结构优化设计[M].北京:水利电力出社,1983.
[5] 隋允康,金雪燕.应力和位移约束下的板壳结构截面优化[J].力学学报,2004,36(6):701-708.
[6] 王晓明,刘震宇,郭东明.基于均匀化理论的微小型柔性结构拓扑优化的敏度分析[J].中国机械工程,1999,10(11):1264-1267.
[7] Pettit R G,Wang J J,Toh C.Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs[M].Hampton:Langley Research Center,2000.
