最优化方法在开发可充电式混合动力车中的应用

顾纪超 周钰亮 李光耀 董佐民 干年妃

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082 2.维多利亚大学,维多利亚,V 8N 3P6

0 引言

牵引控制策略系统直接面对驾驶员的命令和动力系统,是连接驾驶员和动力系统的纽带,在混合动力车中具有举足轻重的作用。主要表现为：牵引控制系统接受驾驶员关于力矩的命令并决定将合适的力矩传递到包括内燃机(ICE)和电动机在内的动力系统中。

理想的牵引系统控制器不但要满足驾驶员关于力矩的命令,还要使能量消耗最少。对于大多数混合动力车的动力传动系统来说,很难甚至不可能只凭借经验就设计出满足所有目标的牵引系统。

确定理想的牵引系统控制器可选择基于优化的方法。这种方法通过将控制器问题转化成带有目标函数和约束的优化问题,使用优化方法得到所需要的参数。目前优秀的建模和仿真工具以及高效的优化方法使解决这样的问题成为可能。

本文选用了几种目前流行的方法——遗传算法(genetic algorithm,GA)[1]、粒子群算法(partical swarm optimization,PSO)[2],以及新近开发的全局最优化方法——基于混合元模型的自适应全局最优化(hybrid and adaptive metamodeling,HAM)方法[3],以期能找到最合适的优化方法,即用最少的时间找到满意的结果。

1 E-REV式混合动力车概述

本文应用一种基于最优化方法的技术来开发E-REV(extended range electric vehicle)式混合动力车的牵引控制系统。E-REV定义了一种在有限范围内带有全电动汽车功能、在扩展范围内带有混合动力车功能的汽车[4]。本文所研究的E-REV电动车以2009SaturnVUE为基本平台,混合动力系统集成一个GM 2-Mode传动系统[5]、一个 Ecotec内燃机(internal-combustion engine,ICE)[6]、一个125k W 的电动机,以及一个高容量电池。汽车的动力系统包含一个内燃机和三个电动机,它们在电池的不同状态下运行。前轮采用带有两个电动机(motbor/generatorA&B)和一个Ecotec 2.4L发动机的2-mode传动系统驱动。后轮采用一个单独安装在后驱动轴上的电动机驱动。当车辆行驶在路上时,前轮牵引和后轮牵引交互使用。在一个全负荷电池驱动下,汽车首先在电动模式下运转60～100km,然后,电池荷电状态(state of charge,SOC)值变小,ICE来提供另外的能量。初步的研究主要致力于解决电动模式下的问题 。

2 优化方法介绍

2.1 遗传算法

遗传算法(GA)是基于遗传学和自然选择机制的搜索算法。Holland通常被认为是遗传算法的创始人,他提出了基础的遗传算法理论[7]。遗传算法的搜索过程包含选择、交叉和变异。目前,遗传算法已经被应用到很多领域中。

2.2 粒子群算法

粒子群算法(PSO)是最近开发出来的全局最优化算法,它起源于自然现象中的粒子群运动。Kennedy等[2]受到自然界中生物的社会行为的启发后研究了飞鸟的行为,于1995年提出了这种算法。粒子群算法有很多优点：使用的函数很简单,易于实现、应用、扩展和杂交化。

2.3 基于混合元模型的自适应全局最优化(HAM)方法

基于混合元模型的自适应全局最优化(HAM)方法是最近为解决计算集中的黑匣子问题而开发的一种只应用近似模型的独立搜索方法。当多个近似模型使用一定数目的样本点同时拟合同一个曲面时,它们所拟合出的曲面很可能出现相同的部分。经过筛选,从这些相同的部分中选择一部分函数值较小的样本点参与近似模型的自适应重建。为了提高样本点的多样性,在其他部分也选取一定数量函数值样本点参与近似模型自适应重建。随着样本点数的增多,近似模型在关注区域的准确程度也随之提高,得到的结果也就越来越接近全局最优值,直至满足收敛条件。

HAM方法将多个具有代表性的近似模型有机结合在一起,充分利用了近似模型的优势,同时将单个近似模型的不利影响降到最低,最大限度地扩展了算法的适用范围。同时,能够从备选的近似模型中自动选择最适合解决未知问题的近似模型进行计算,具有一定的智能。此外,重点空间的定义提高了算法的精度和效率。其主要步骤如下：

(1)生成初始点,并调用计算集中的目标函数计算这些“昂贵”的样本点的 函数值。初始样本点的个数通常比较少,这些点应用“空间覆盖”方法选取,并计算其函数值来构造元模型 ˆf(x)、(x)和(x),这三个元模型分别为Kriging模型[8-9]、径向基函数[10]和二阶多项式响应面[11]。这三种元模型各具特点,经过有机组合,使算法的适用范围大大增加。三种元模型的可能组合方式有7种,会产生7个子空间。如果平均从每个子空间中选取一个样本点,那么每次迭代就会选取7个左右的样本点。为了平衡初始点和第一次迭代的样本点的比率,初始点的数目与每次迭代所选取的数目要相同。为了避免四舍五入会增加选取样本点数目的问题,初始点的数目定义为8。

(2)选取大量的样本点,并用三个元模型分别计算。在这一步中会使用拉丁超立方采样方法(latin hypercube design,LHD)生成大量的样本点,其函数值用元模型计算。由于元模型具有计算快速的特点,所以这些点又叫做“便宜”点。这些点的计算量很小,所以数目可以定义得非常大,推荐为104。

(3)根据函数值给这些样本点排序。这些“便宜”点根据元模型计算得到的函数值升序排列,并根据所参与计算的元模型的不同将它们分成不同的组。前m个函数值最小的点将被选出来放到不同的组中,即 ˆf(x)选择的m个点放到A组中,ˆg(x)选择的m个点放到B组中,ˆh(X)选择的m个点放到C组中。

(4)将上一步选出的点分组。将这些点根据出现在不同的组的数目分成7个部分：E=A∩B∩C,F=A∩B,G=B∩C,H=A∩C,I=A-F,J=B-G,K=C-H。从以上 7个部分中选择大约共7个新的样本点,并调用目标函数计算,成为新的“昂贵”点。

(5)计算每个部分的权值。每个部分将根据点的数目以及重要程度定义权值作为在其中选取样本点数目的依据。权值的和为1。

(6)选择新的“昂贵”点。每个组中根据权值的不同会选出一些点,这些点将和以前的“昂贵”点一起参与元模型的重建。

(7)重复迭代直到算法收敛。将所有的“昂贵”点合并到一起,重新构建元模型,并重复步骤(2)～(6)直到满足收敛条件。此方法的详细介绍可见文献[3]。

3 优化问题定义及结果

3.1 牵引控制系统开发流程

本文主要应用最优化方法开发混合动力车中的牵引控制系统,基于最优化方法的牵引控制系统开发流程见图1。

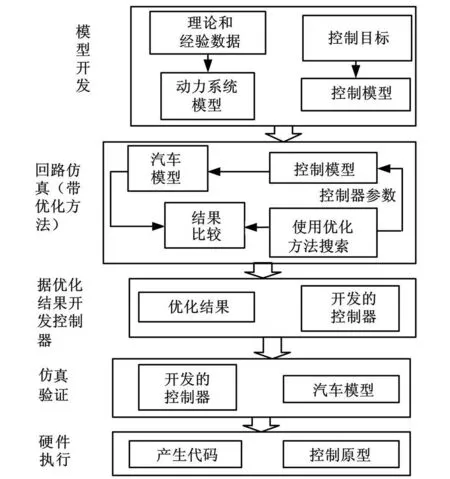
图1 牵引控制系统开发流程

3.2 问题定义

汽车的仿真模型在MATLAB和dSpace环境中开发,汽车部件的模型由原仪器制造商提供。应用建立的高精度仿真模型,汽车的性能可以通过仿真得到,电子控制元件进行编程操作也可以通过仿真进行。

当在电动汽车模式下运行时,2-mode混合动力车选择从 2-mode传动系统(发动机不参与)和后牵引电机处获取功率。从2-mode系统和后牵引电机得到的混合功率要满足驾驶员的力矩命令。为定义优化问题,首先定义一个关于汽车速度(X轴)和需要的功率(Y轴)的表格,表格中的每个点代表一种操作条件,对应一个力矩值,通过得到合适的力矩来得到电机的最优效率。在这个表格中,速度的范围为：-0.5～54km/h,每隔1.8km/h取一个点;功率的范围定义为：-65～93.75k W,每隔1.25k W取一个点。整个表格一共32行,128列,4096个点,即需要进行4096次优化。优化问题由以下的函数定义：

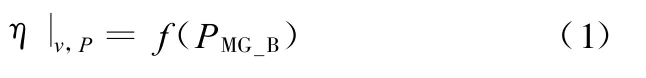
其中,η为电力/机械功率转换效率。v和P分别为汽车速度和需要的功率。P MG_B为需要从建立的2-mode传动系统中的其中一个电机处得到的功率。函数的结果通过运行回路中的模型得到。汽车系统中有大量的设计约束。由于在仿真时,如果不满足约束,模型就不会有结果,只输出一个NAN(not a number),所以在优化这一步中并不需要定义约束。

首先采用局部最优化方法解决式(1)定义的优化问题,然而,结果并不能令人满意,主要有两个原因：①当初始点改变时,结果也随之改变,这就意味着这个问题并不是一个单峰值问题;②基于梯度的方法经常出现错误,而不能完成对这个问题的优化,主要是因为在这个问题中,一些点处的梯度值很难获得,可见基于梯度的局部最优化方法不能应用于当前的问题中。

3.3 优化结果

此模型应用遗传算法[12]、粒子群优化算法[13]和HAM 方法进行优化,以得到最好的结果,为后续工作选择最合适的方法。遗传算法的代码可以从MATLAB最优化工具箱中得到[12],粒子群优化算法的代码可以从网页上下载[13]。这三组结果中每个点的最优结果组成一个准最优结果,即准最优结果中的每个点的结果都是这三组结果中最小的。结果质量和计算时间见表1。结果质量代表每个方法得到的结果与准最优结果的平均偏差,即数值越小,越接近准最优结果。与准最优结果比较的统计结果见表2,其中Mean表示与准最优结果的偏差值,N表示结果的个数。

表1 优化结果

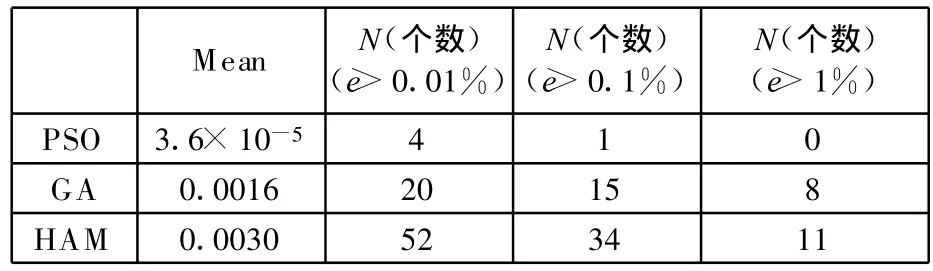
表2 与准最优结果比较的统计结果

从表2可以看出,使用PSO方法得到的结果最精确,与准最优结果最接近。设所得结果与准最优结果偏差为e,在这120个点中,只有1个点的结果与准最优结果偏差大于0.1%以上,绝大部分结果与准最优的偏差小于0.01%。使用遗传算法得到的结果精度介于PSO算法和HAM算法之间,HAM方法得到的结果精度最差,但是与遗传算法得到的结果精度相似,与准最优结果的平均偏差也只有0.0030,足够满足需要。就计算时间来说,PSO方法所用的时间远远大于遗传算法和HAM方法所用的时间,而HAM方法用的时间最短,只有PSO方法使用时间的1.6%、遗传算法使用时间的5.5%。遗传算法使用的计算时间介于PSO算法和HAM算法之间。当只优化120个点的较粗糙的模型时 ,PSO算法要花费549min的时间,而HAM算法只需要14.4min就可以完成优化,遗传算法也需要240min。可见,HAM方法在精度和效率之间取得了很好的平衡,在满足精度要求的条件下,获得了足够准确的结果。

3.4 仿真结果

将优化结果集成到控制器模型中,就可以通过仿真模型将需要的结果输出来。为了进行比较,将创建另一个使用简单控制规则的模型,这个模型均匀地将功率分配给每个电动机。仿真使用NYCC(New York city cycle)驱动循环。

使用简单规则和基于优化的规则的电机/发电机B的效率比较如图2所示。

图2 电机/发电机 B的效率比较

仿真结果表明,基于优化的控制器模型较大幅度地提高了能量使用效率,在原模型平均效率约为82%的基础上,大约平均提高了3%～5%。

与之相同,图3比较了后牵引电机的能量使用效率。使用基于优化的控制器模型的效率同样得到了提高。

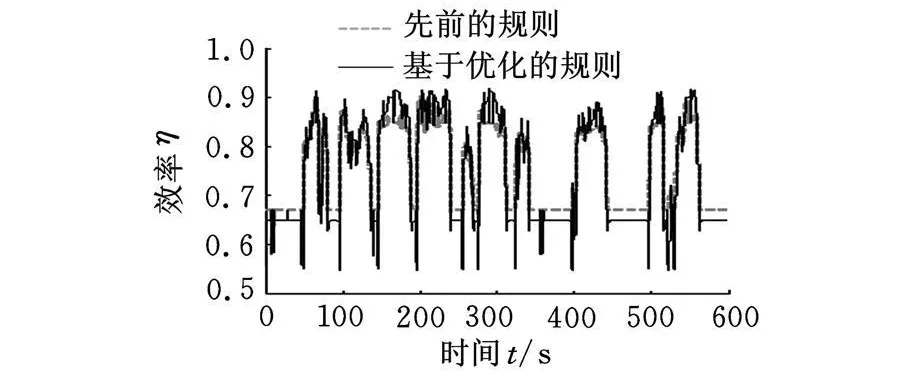
图3 后牵引电机效率比较

4 结束语

本文应用多种全局最优化方法对牵引控制系统进行了优化,相对于先前应用简单的规则,应用基于优化的规则,整个模型的效率以及后牵引电机的效率都得到了提高。

在所应用的三种方法中,PSO方法虽然得到的结果最为精确,但是所用的计算时间使其难以继续应用于后续工作;遗传算法得到的结果精度稍差于PSO方法,居于第二位,同样满足要求,所用的计算时间也少于PSO方法,但是所用的计算时间同样难以接受;HAM方法综合考虑精度和效率,在精度和效率之间取得了很好的平衡,用远远少于PSO和遗传算法的计算时间得到了相似精度的结果,后续的工作中将应用HAM方法。

[1] Goldberg D E.Genetic Algorithms in Search,Optimization and Machine Learnin[M].New Jersey：Addison-Wesley,1989.

[2] Kennedy J,Eberhart RC.Particle Swarm Optimization[C]//IEEE International Conference on Neural Networks.Perth,1995：1942-1948.

[3] Gu J,Li G Y,Dong Z.Hybrid and Adaptive Metamodel Based Global Optimization[C]//Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.San Diego,2009：751-756.

[4] Morris R.Chevrolet Volt-GM's Concept Electric Vehicle——Could Nearly Eliminate Trips to the Gas Station[J].Battery Power Products and Technology,2007,11(2)：1.

[5] Jost K.GM's Hybrid SUVs：Best AEI Engineered Vehicle 2008[J].Automotive Engineer,2008,33：65-70.

[6] General M.CPGM2_10E0G6MA J1349 Certified Power Engine Data for GM LE9 Ecotec as Used in 2010 Pontiac G6,2010 Chevrolet Malibu,2010 Saturn Aura,LE9 Ecotec Engine Operating on E0-Level 2[S].Detroit：SAE,2009.

[7] Holland J H.Adaptation in Natural and Artificial Systems[M].Boston：MIT Press,1975.

[8] Cresssie N.Spatial Prediction and Ordinary Kriging[J].Math.Geol.,1988,20(4)：405-421.

[9] Simpson T W,Allen JK,Mistree F.Spatial Correlation Metamodels for Global Approximation in Structural Design Optimization[C]//Presented at the Proceedings of DETC98 1998 ASME Design Engineering Technical Conference.Atlanta,1998：ASME DETC98/DAC-5613.

[10] Hardy R L.Multiquadratic Equations of Topography and Other Irregular Surfaces[J].J.Geophus.Res.,1971,76：1905-1915.

[11] Box G E P,Wilson K B.On the Experimental Attainment of Optimum Conditions[J].Journal of royal Statistics Society,1951,13：1-45.

[12] Mathworks.Matlab 7.7 User Guide：Optimization Toolbox[M].MA：the Math Works,Inc.,2008.

[13] Birge B.PSOt-a Particle Swarm Optimization Toolbox for Matlab[EB/OL].http：//ieeexplore.ieee.org/xpls/abs_ all.jsp? arnumber =1202265&tag=1