具有稳定相位中心的三馈点圆极化微带天线
2011-05-29张福顺焦永昌
林 晨 张福顺 朱 杨 张 凡 焦永昌
(西安电子科技大学天线与微波技术重点实验室,陕西 西安 710071)
1.引 言
一般实现圆极化天线的基本原理就是产生两个空间上正交的线极化电场分量,并使二者振幅相等,相位相差90°。而如何满足这个圆极化的条件,不同的天线有不同的实现方式。常见的微带天线激励圆极化的方法,主要分为单馈和双馈。单馈的微带圆极化天线主要通过破坏平衡性来实现圆极化波的产生,而双馈则按照圆极化波产生的三个要素进行设计,即空间正交、幅度相等、相位相差90°。单馈微带圆极化天线[1-2]固有的窄带特性限制其只能工作在局部频点。双馈方式[3-4]具有相对较宽的阻抗和轴比带宽,得到了广泛的应用。
历年来对微带天线的研究重点都在改善带宽、提高增益上,对其相位中心的稳定性研究甚少。随着GPS、北斗、测向等多种先进无线电系统的广泛应用,以及定位及测向精度的提高,天线相位中心的位置[5-7]及其稳定性对系统测试精度的影响已不可忽略,因此,设计具有稳定相位中心的天线,以及标定相位中心稳定性日益受到人们的重视[8-10]。本文正是基于这些应用提出了一种三馈点圆形微带天线,通过均匀对称馈电方法改善了相位中心的稳定性。笔者从理论上推导出三馈点圆形微带天线获得圆极化的馈电条件。与传统双馈设计相比,新的结构对相位方向图的周向对称性有了极大的改善,保证了相位中心的稳定。本文研究了该天线的工作机
理和性能,给出了仿真和实验结果。
2.天线设计与仿真结果
2.1 天线结构设计
天线的相位中心稳定度与天线的形式和馈电方式相关。一般来说,天线的对称性越好,馈电点数目越多,馈电点越对称,其相位中心的稳定度越高。因此,为解决双馈点天线相位中心不稳定的问题,提出了一种新颖的三馈点天线。图1给出了三馈点微带天线的结构图。如图所示,天线采用半径为Rp的圆形微带贴片作为辐射器,并具有三个关于圆心对称的馈电点,从而保证了相位中心稳定和良好圆极化所需要的对称性。天线的三个馈电点均匀地分布在半径为D的圆周上。为展宽阻抗带宽,设计采用厚度较大(H= 4 mm),介电常数较低(εr=2.65)的介质基板,其损耗角正切值为0.003。天线的金属地板同样采用圆形,其半径为Rg.圆形微带天线工作在主模(TM11模),中心频率为f0= 2.45 GHz.使用圆形微带贴片设计经验公式[11],计入边缘效应,可得到实际的物理尺寸。背馈式馈电通过传输线法[11]可估算出馈电点的位置。
经计算天线工作于频率f0时,贴片半径Rp= 20.3 mm,馈电点位置D= 5.5 mm(单个馈电点)。利用基于有限元法的软件高频电磁仿真软件(HFSS)对贴片单元(三个馈电点)进行仿真分析, 微调谐振频率和输入阻抗。调整后天线实际尺寸: 贴片半径Rp= 21.2 mm,馈电位置D= 8.0 mm,基板半径Rs= 30.0 mm,地板半径Rg= 40.0 mm.图2给出了天线各端口反射系数的仿真结果。从图中可以看出:在频段2.38 ~ 2.53 GHz内,天线三个端口的反射系数曲线基本一致,且均小于-10 dB.
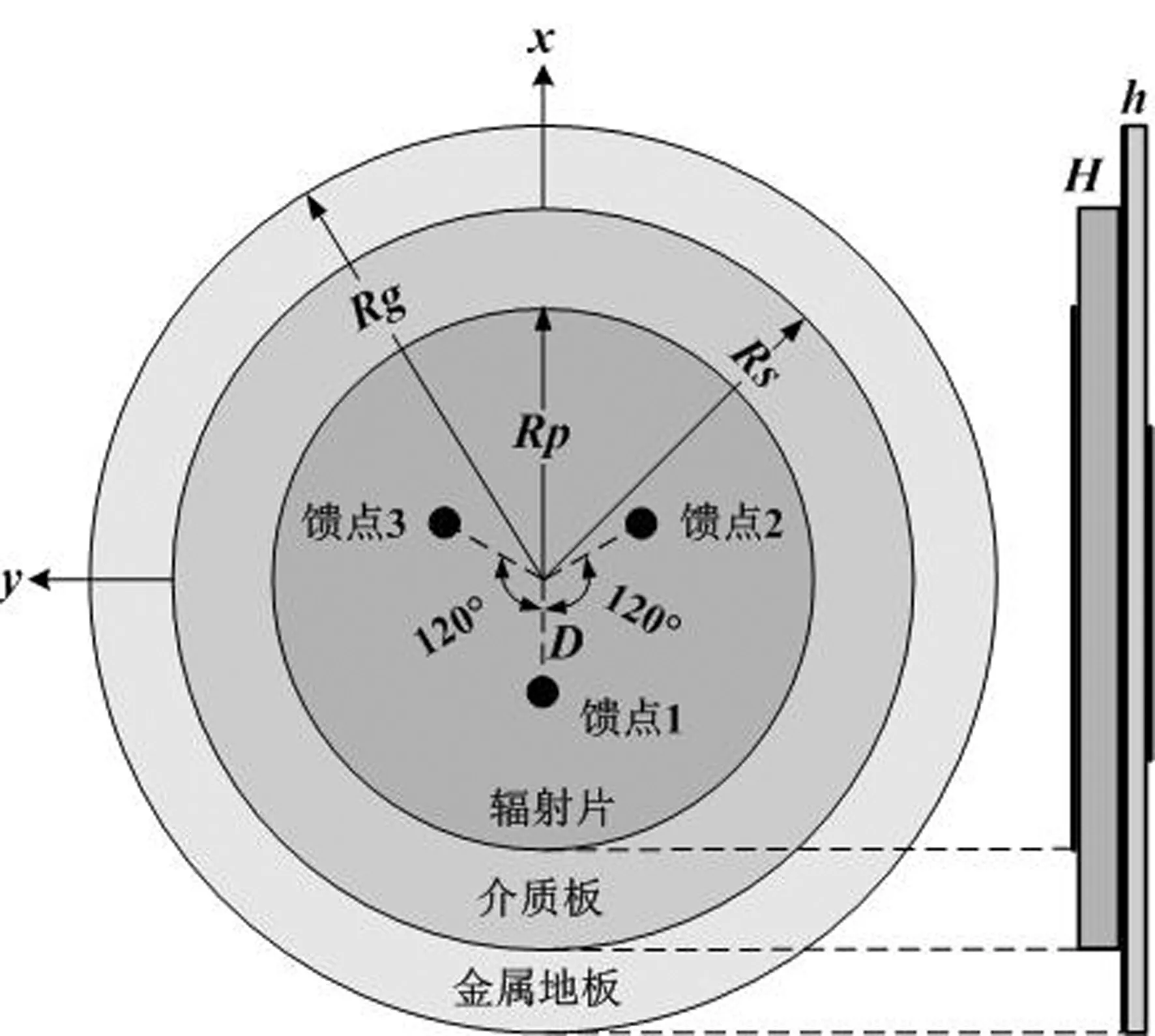
图1 三馈点圆形微带天线结构示意图
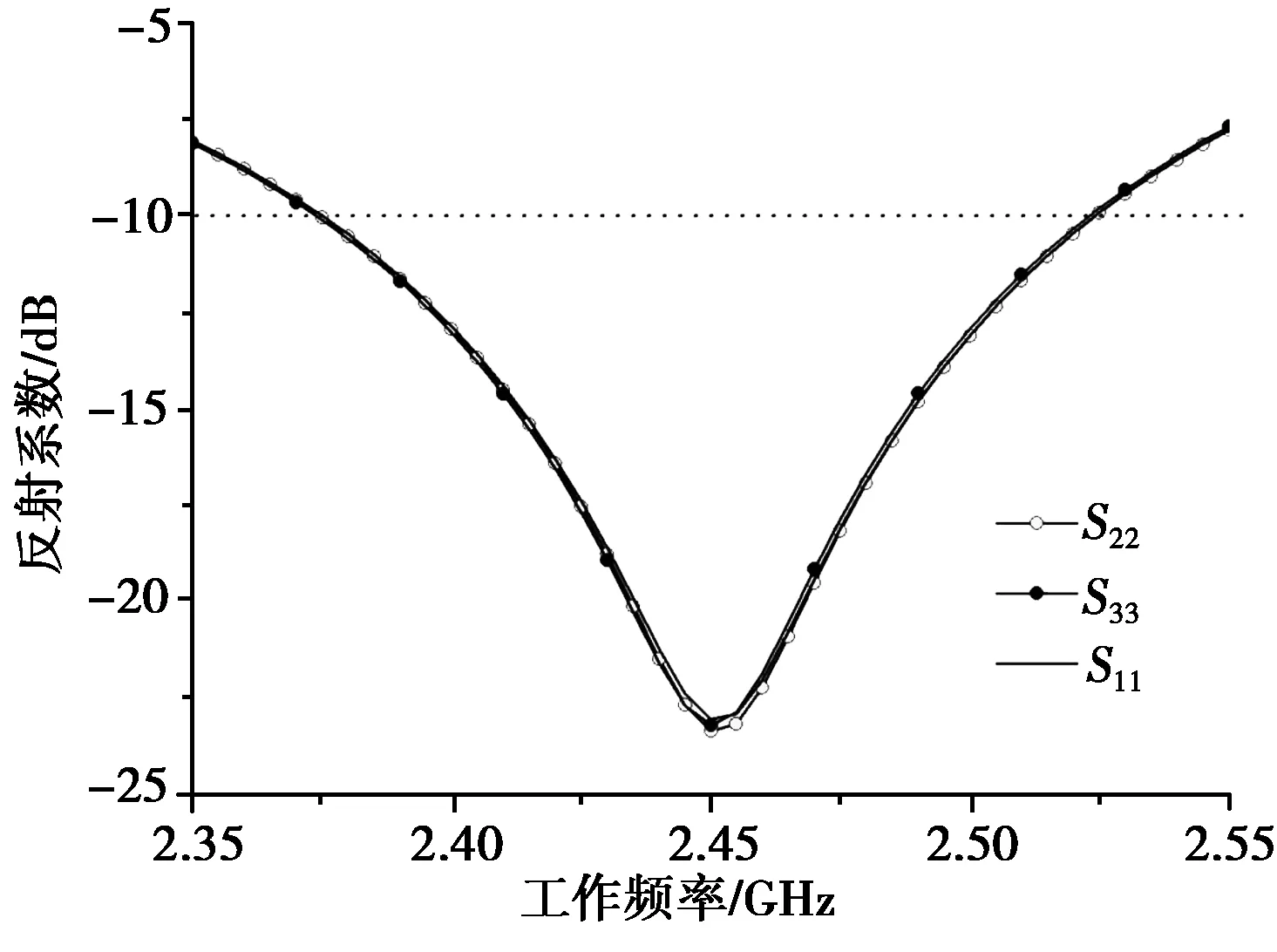
图2 天线各端口反射系数仿真结果
2.2 馈电方法分析
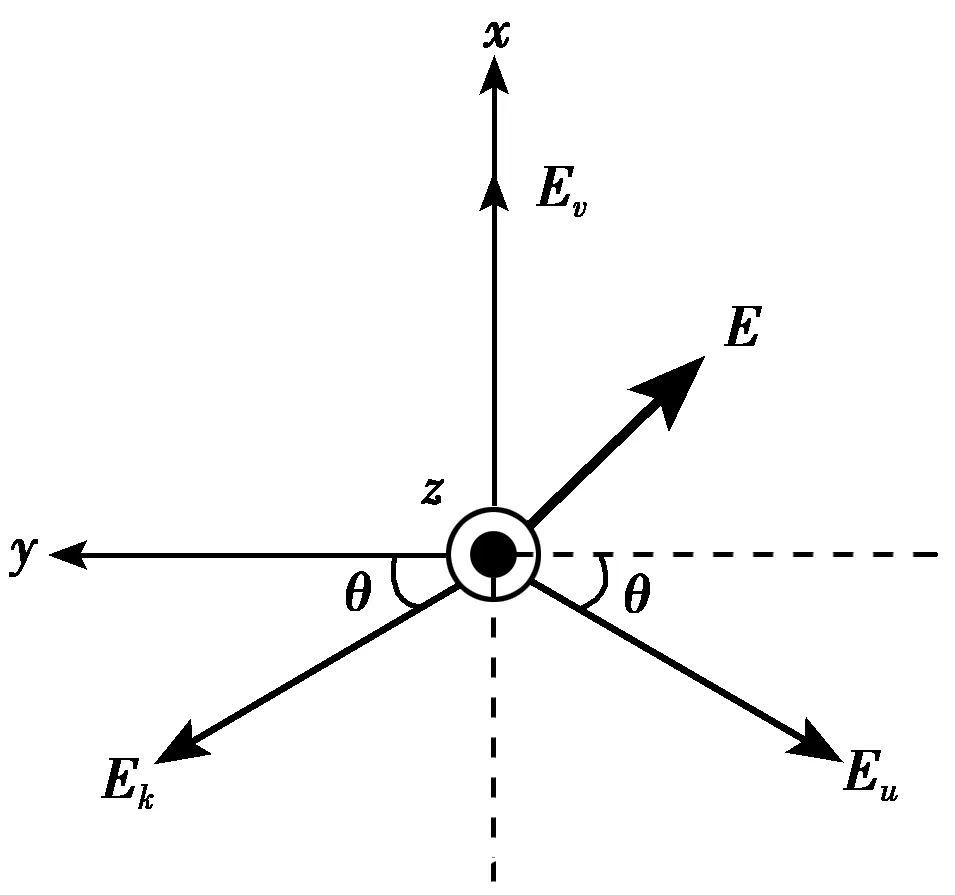
图3 电场矢量分布示意图
其电场作为时间和位置的空间函数,可分别写成
Eu=E1sin(wt-βz-φ)
(1)
Ev=E2sin(wt-βz)
(2)
Ek=E3sin(wt-βz+φ)
(3)
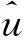
E=Ev+Eu+Ek
φ)cosθ-E1sin(wt-βz-φ)cosθ]
(4)
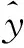
Ex=E0[sin(wt)-sin(wt+φ)sinθ-sin(wt-φ)sinθ]
(5)
Ey=E0[sin(wt+φ)cosθ-sin(wt-φ)cosθ]
(6)
展开式(5)和式(6)有
Ex=E0[sin(wt)-2sin(wt)cosφsinθ]
(7)
Ey=E0[2cos(wt)cosθsinφ]
(8)
由Ex和Ey的关系分别有
(9)
(10)
合并式(9)和式(10),消掉wt,整理得出
(11)
由式(11)可以看出,当两个分母相等时,合成场矢量的轨迹是一个圆,获得了圆极化特性。即φ和θ需要满足如下方程
(1-2cosφsinθ)2=(2cosθsinφ)2
(12)
根据天线馈电点位置可知θ=30°,并带入到公式(12),解得相位差φ=∓120°,分别对应右旋和左旋极化波。
在HFSS中采用三个理想的等幅激励源对天线馈电进行仿真验证。当激励源之间的相差从90°变化到150°时,分别计算了天线在频带2.0 ~ 3.0 GHz内的轴比。如图4所示,当相差为90°时,天线在频带内的轴比均大于4 dB;随着相差增大,轴比变好,且相差为120°时其达到最好值;当相差进一步增大时,轴比则开始变差。仿真结果验证了理论推导的正确性。
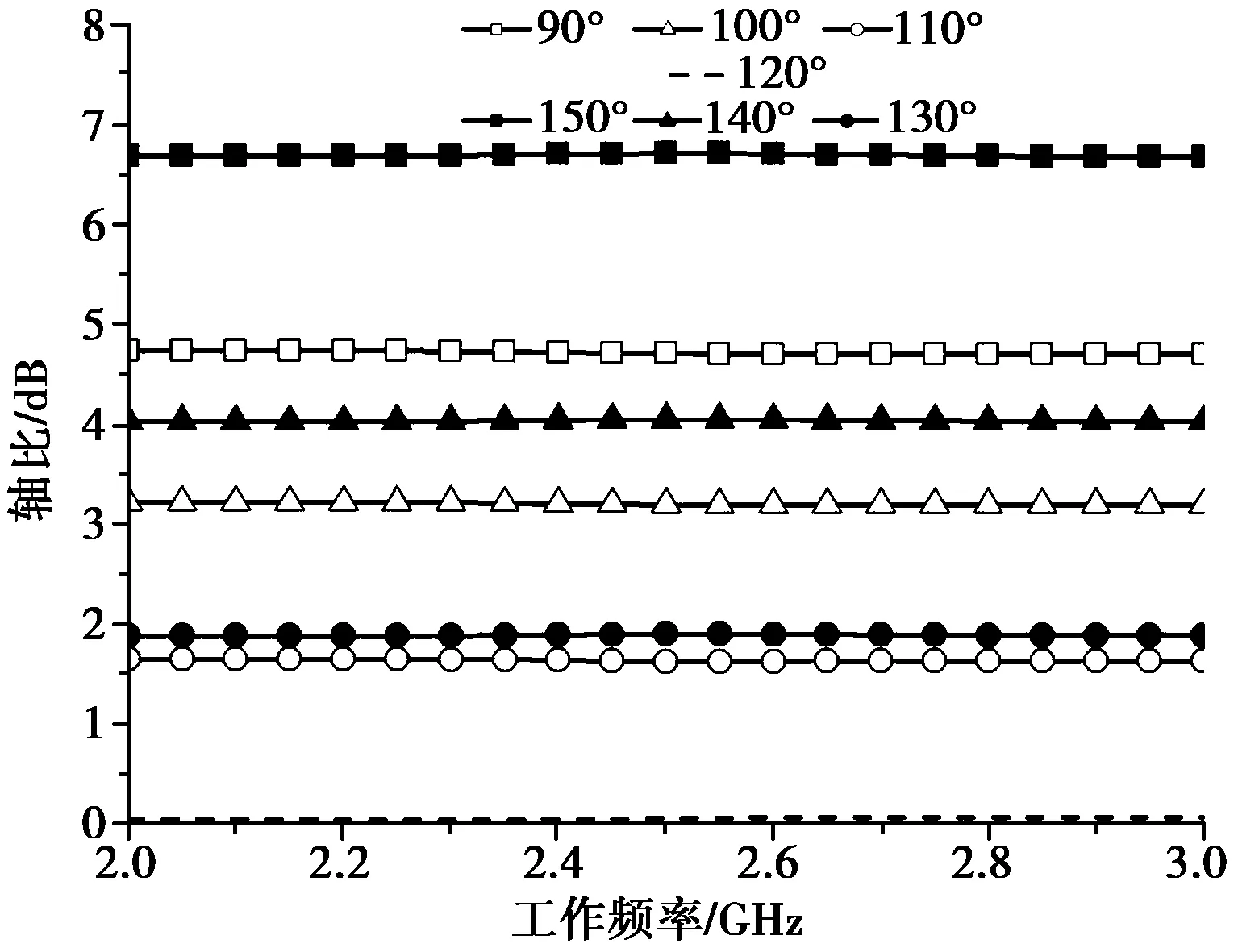
图4 天线轴比随相位差变化仿真结果
2.3 馈电网络结构设计
根据理论分析结果,设计天线馈电网络,提供三个幅度相等,相位相差120°的激励。为便于工程实现,设计了一个常用的一分三Wilkison功率分配器。如图5所示,三条电长度分别相差1/3波长(f0= 2.45 GHz)的微带线分别连接到功率分配器的各输出端口,实现超前或滞后120°的相位差。功率分配器采用较薄(h=1 mm)的圆形介质基板(εr=2.65),安装于微带天线下方并与其共用一个金属地板。
在仿真中,用功率分配器代替理想激励源对天线馈电,其电性能仿真结果如图6所示。从图6(a)中可以看出:天线反射系数S11< -10 dB的带宽为550 MHz(2.18 ~ 2.73 GHz)。图6(b)给出天线轴比曲线图,其3 dB轴比带宽为470 MHz (2.24 ~ 2.71 GHz)。由于微带线实现120°相差的带宽具有窄带特性,天线无法获得很宽的轴比带宽。
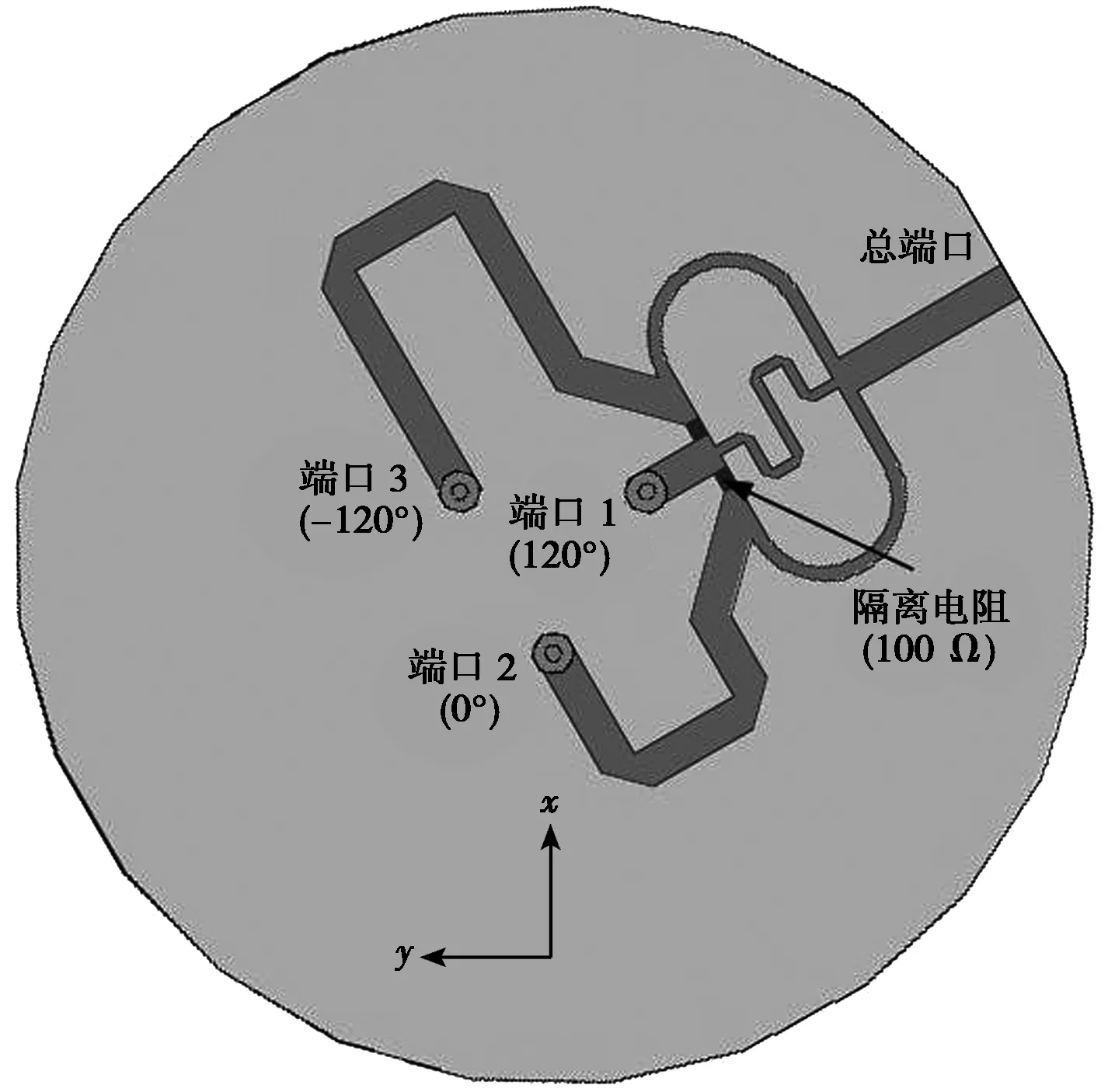
图5 Wilkison功率分配器结构示意图
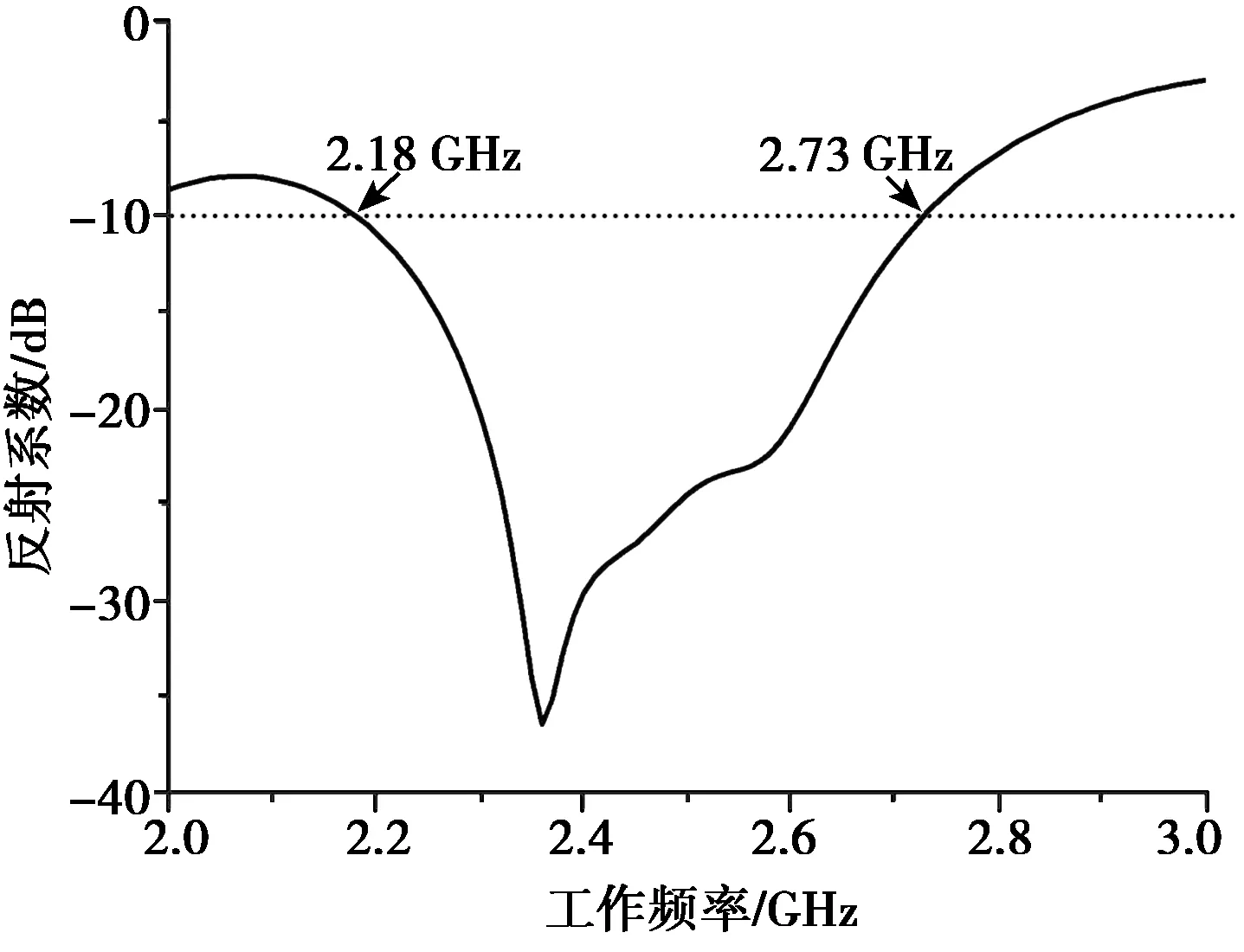
(a) 天线反射系数仿真结果
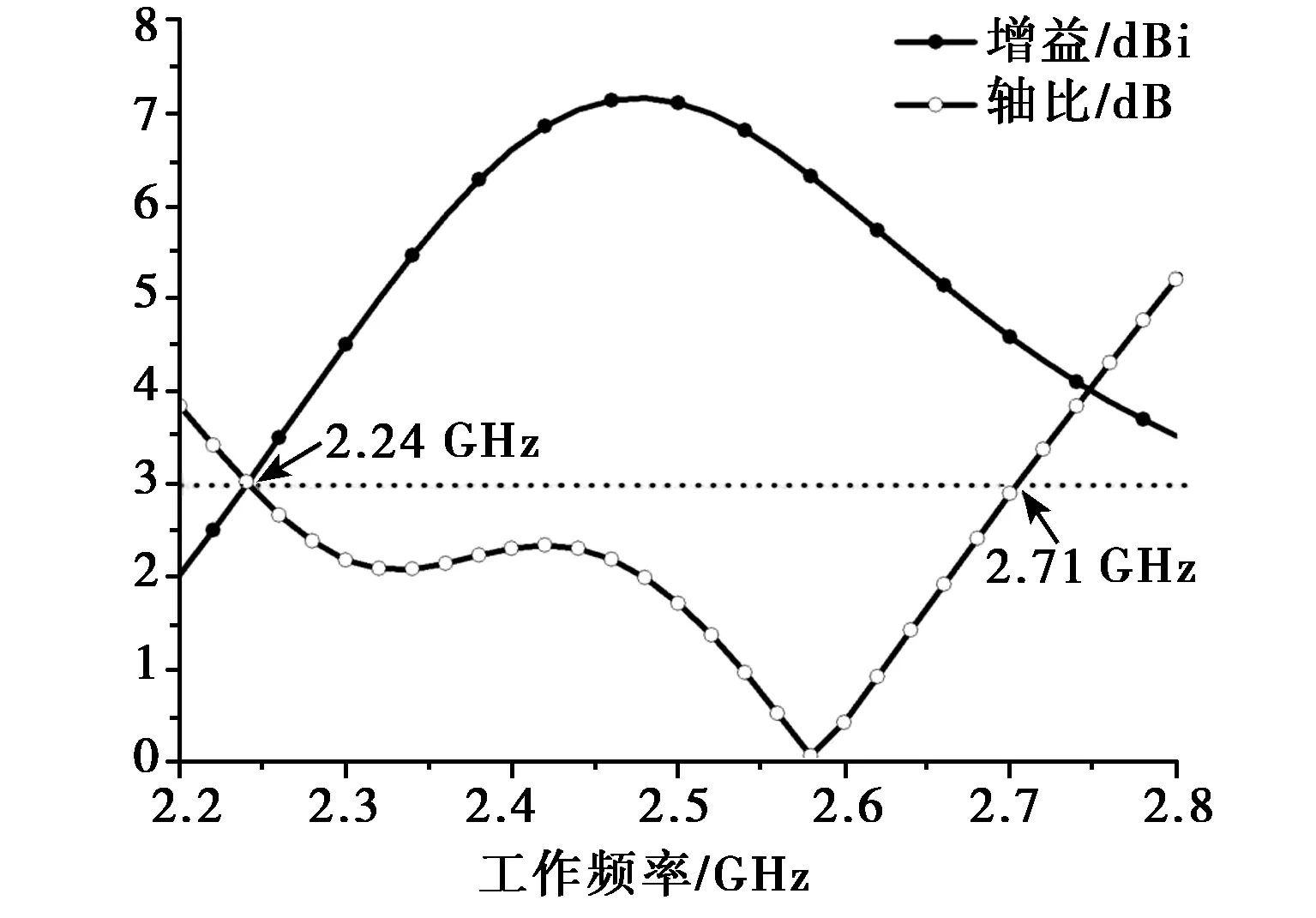
(b) 天线轴比和增益仿真结果图6 三馈点微带天线电性能仿真结果
2.4 天线相位中心标定
通常只能在天线主波束的一定角度范围内,近似找到一点,使得远场相位方向图的相位波动最小,这个点称为天线的视在“相位中心”。天线的相位中心稳定度是表征天线各个切面相位中心离散程度的量,是包含天线各个切面的相位中心点的球体的最小半径[9],其球心可以近似认为是视在相位中心。虽然天线本身的设计已经保证了较高的相位中心稳定度,但仍需通过试验或仿真的方法将相位中心稳定度标定出来。天线相位中心稳定性的标定方法有三种[12]:仿真计算、微波暗室测量和接收机系统测试。前两种方法得到的是天线的绝对相位中心,后一种方法得到的是天线的相对相位中心。本文采用第一种方法对天线的相位中心进行标定。
在最小二乘意义下[13],采用解析法计算出该天线和双馈点天线各个切面的相位中心和稳定度,结果见表1和表2。其中,参考点(0,0,0)位于天线地板圆心,天线phi隔30°取一个面,theta在±50°范围内每隔1°取一个点。对比结果可以看出:三馈点天线的相位中心稳定度小于1 mm,相位波动小于3.5°,均明显优于双馈方式。
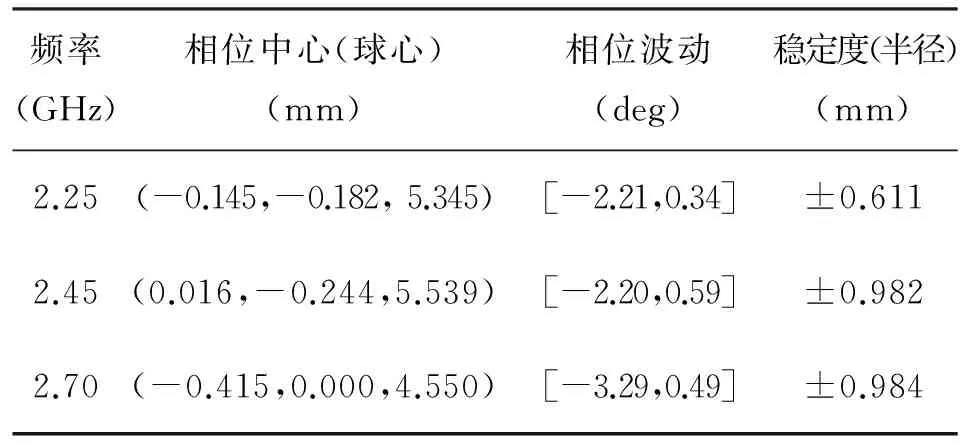
表1 相位中心稳定度计算结果(三馈点)
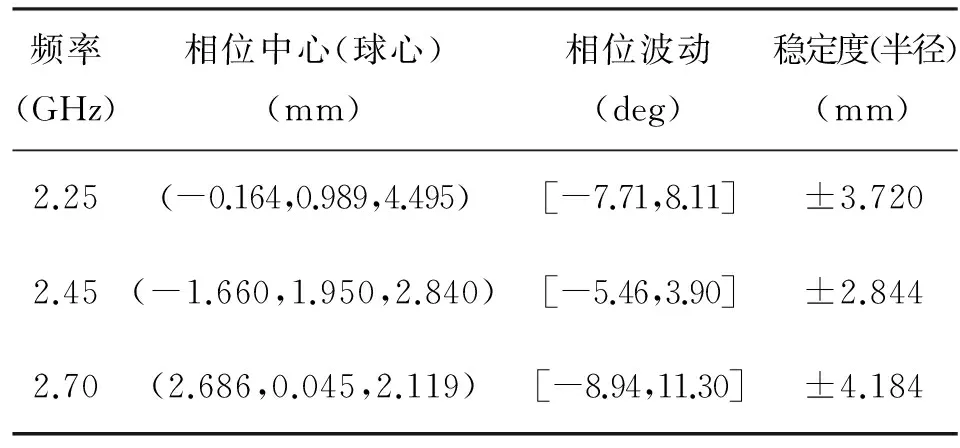
表2 相们中心稳定度计算结果(双馈点)
但是在实际应用中,需要在波束空间内确定一个稳定的相位中心。而包含各个切面相位中心的最小半径球体的球心,并不能代表同时考虑整个波束空间的相位中心。为了描述这种波束空间内的天线相位中心,需要引入平均(视在)相位中心的概念。平均相位中心的含义为:整个天线波束空间内的实际等相面如果用一个理想等相球面来拟合,拟合残差的平方和最小,则拟合球面的球心即为天线的平均相位中心。
采用解析法计算天线的平均相位中心过于复杂,而通过优化算法对天线平均相位中心进行标定则相对简单。平均相位中心的标定是通过计算立体角内各点相位,优化天线在参考坐标系中的位置进行的。其一般步骤如下:
1) 仿真软件计算得到天线在参考坐标下立体角内各点相位;
2) 通过优化算法更新机制,得到一组天线相对参考坐标的新位置;
3) 根据相位方向图变化规律,计算得到天线在某新位置下立体角内各点相位;
4) 根据视在相心的定义,对每新位置求出线性最小二乘意义下的相位最平坦值[13](适应度值);
5) 重复步骤2)~4),直到天线在立体角内每个切面的相位方向图近似为直线。
利用HFSS软件仿真得到天线立体角内各点相位。同样,参考点(0,0,0)位于天线地板圆心,天线phi隔30°取一个面,theta在±50°范围内每隔1°取一个点。表3给出了通过优化算法得到天线的平均相位中心,图7则给出了按0°方向修正后的相位方向图。从仿真数据可以看出:在平均相位中心上,相位波动小于1.2°。因此,对比表1中最小半径球心上的相位波动,平均相位中心更适合作为整个波束空间的相位中心。
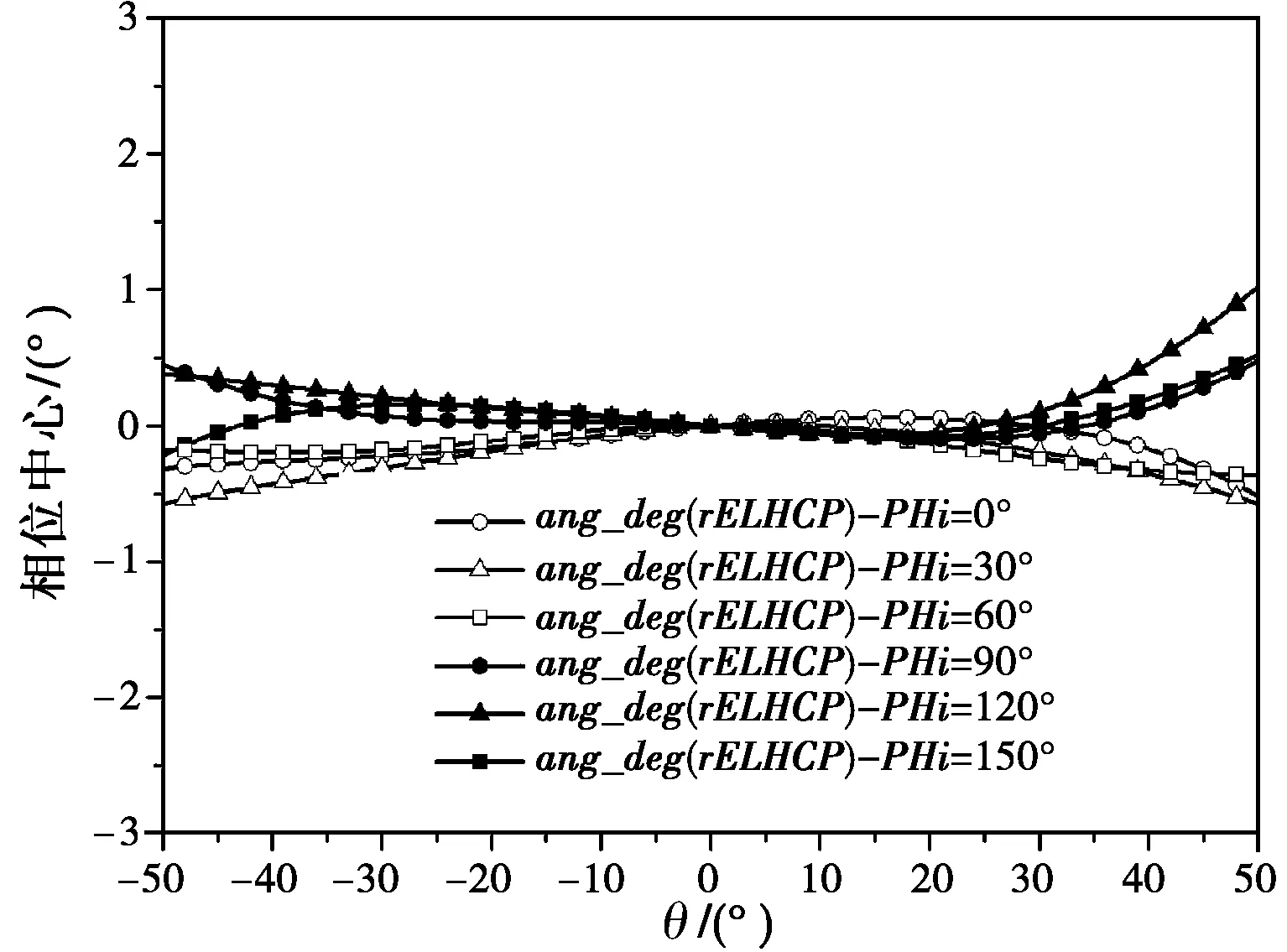
(a) f = 2.25 GHz
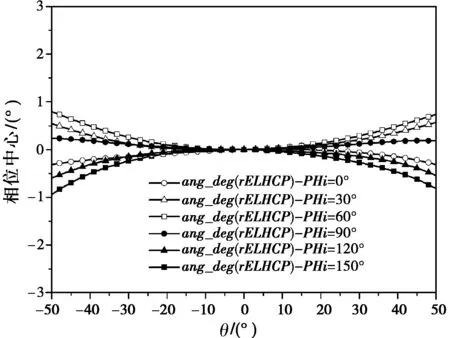
(b) f = 2.45 GHz
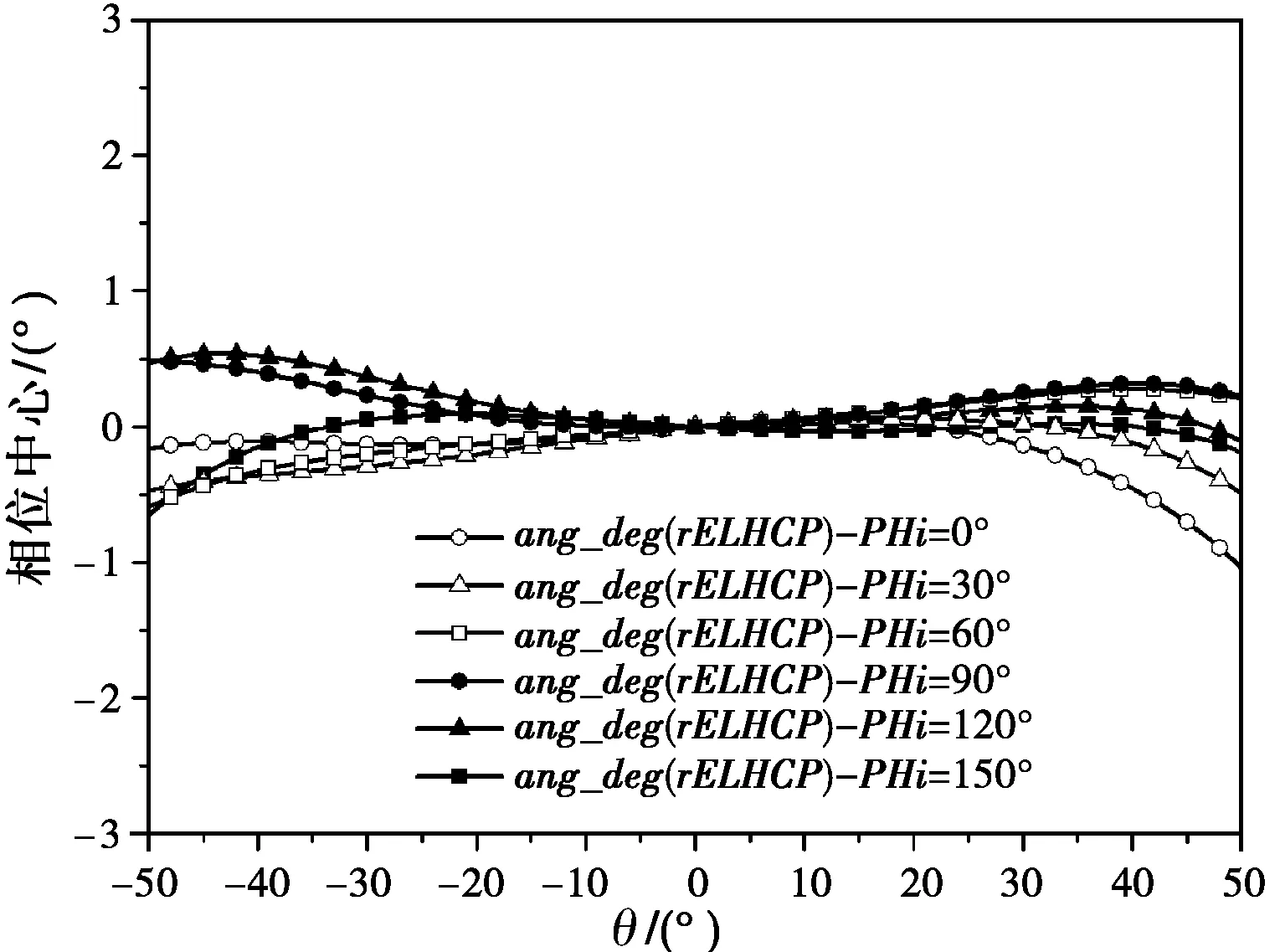
(c) f = 2.70 GHz图7 天线各频率修正相位方向图
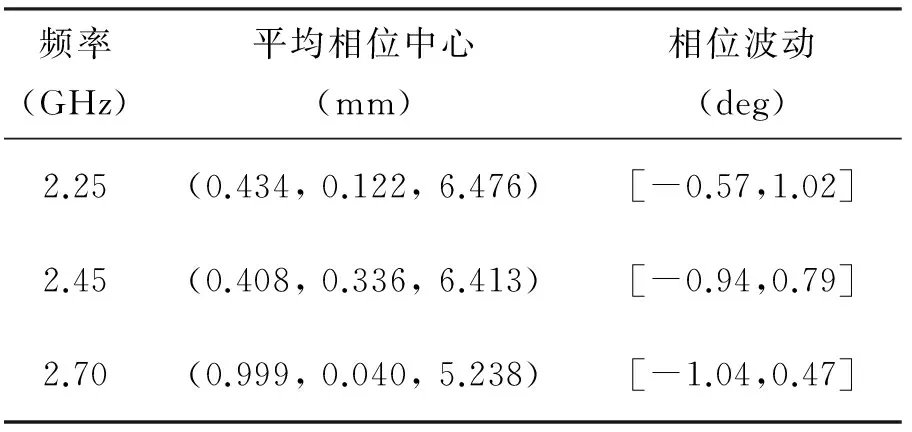
表3 平均相位中心优化计算结果(三馈点)
3. 实验结果
在仿真的基础上,制作了实物并进行了相关测试。图8给出了天线实物的正面和背面,正面中心部分为圆形辐射片,并利用三个直径1.6 mm的金属铜柱,垂直地穿过介质基板和金属地(由隔离孔隔开),连接辐射片和功率分配器输出端口。使用矢量网络分析仪(WILTRON37269A)测试天线的反射系数曲线,结果如图9所示。对比仿真和实测结果可以看出:除了实际测试结果偏向低频外,两者基本吻合。测试结果偏低频的原因:1)印制板介电常数的本身误差,2)加工制作的精度误差,3)测量本身引入的误差。仿真和实物的偏差可通过后期对实物的修正加以解决。图10给出了天线xoz面和yoz面辐射方向图的实测结果。图11给出了天线增益和轴比的实测结果。

图8 三馈点微带天线实物照片
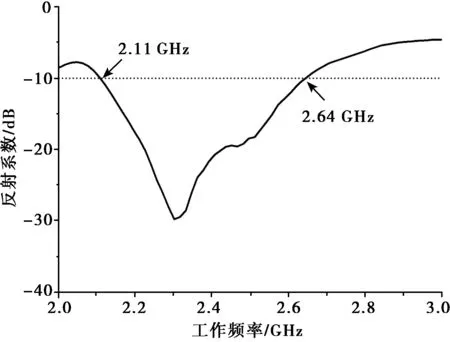
图9 天线反射系数实测结果
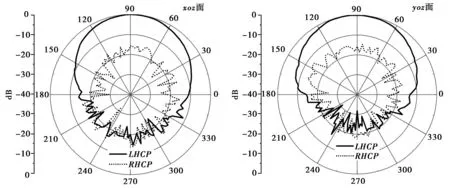
(c) 2.65 GHz图10 天线辐射方向图实测结果
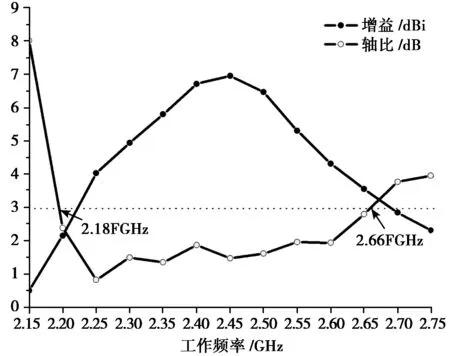
图11 天线增益与轴比实测结果
4. 结 论
本文提出一种新颖的三馈点微带天线。该天线在一定带宽内实现了圆极化特性,并有较高的相位中心稳定度。优化计算结果表明:在整个工作带宽内,天线相位中心的稳定度在1 mm内。同时,本文还给出了三馈点天线能获得圆极化辐射的理论推导。利用电磁场仿真软件HFSS对天线模型进行了仿真,并制作了天线初样产品,仿真结果和实测结果一致性较好,验证了理论推导和天线设计的正确性。因此,该天线结构可以应用在定位及测向系统的终端设备中。
[1] CHEN H M, WANG Y K, LIN Y F, et al. Microstrip-Fed Circularly Polarized Square-Ring Patch Antenna for GPS Applications[J]. IEEE Trans on AP, 2009, 57(4): 1264-1267.
[2] TONG K F, WONG T P. Circularly Polarized U-Slot Antenna[J]. IEEE Trans on AP, 2007, 55(8): 2382-2385.
[3] MAK K M, LUK K M. A Circularly Polarized Antenna With Wide Axial Ratio Beamwidth[J]. IEEE Trans on AP, 2009, 57(10): 3309-3312.
[4] WONG K L, CHIOU T W. Broad-band single-patch circularly polarized microstrip antenna with dual capacitively coupled feeds[J]. IEEE Trans on AP, 2001, 49(1): 41-44.
[5] 金元松,董明玉,何绍林,等.对数周期偶极子天线的可变相位中心[J].电波科学学报, 2001, 16(3):323-328.
JIN Yuansong, DONG Mingyu, HE Shaolin, et al.The variable phase center of the log-periodic dipole an-tenna[J]. Chinese Journal of Radio Science, 2001, 16(3): 323-328. (in Chinese)
[6] 唐 璞,李 欣,王 建,等.计算天线相位中心的移动参考点法[J].电波科学学报, 2005, 20(6): 725-728.
TANG Pu, LI Xin, WANG Jian, et al. Calculation of phase center for the antenna with the method of mov-ing reference point[J]. Chinese Journal of Radio Sci-ence, 2005, 20(6): 725-728. (in Chinese)
[7] 金元松,任晓飞,冀海鸣,等.对数周期偶极子天线全空间可变相位中心[J].电波科学学报, 2007, 22(2): 229-233.
JIN Yuansong, REN Xiaofei, JI Haiming, et al. Var-iable phase center of the log-periodic dipole antenna in full space[J]. Chinese Journal of Radio Science, 2007,22(2): 229-233. (in Chinese)
[8] DOZAR D M, DUFFY S M. A dual-band circularly polarized aperture-coupled stacked microstrip antenna for global positioning satellite[J]. IEEE Trans on Antennas and Propagation, 1997, 45(11): 1618-1625.
[9] 丁克乾,何炳清. 一种星载高相位中心稳定度双频GPS天线[J]. 遥测遥控, 2007, 28(11): 182-186.
DING Keqian, HE Bingqing. A dual band GPS antenna with high stability of phase center used on satellites[J]. Journal of Telemetry, Tracking and Comman, 2007, 28(11): 182-186. (in Chinese)
[10] 何炳清, 丁克乾. 天线相位中心的推算及标定[J]. 遥测遥控, 2009, 30(6): 66-69.
HE Bingqing, DING Keqian. Calculation and measurement of antenna phase center[J]. Journal of Telemetry, Tracking and Comman, 2009, 30 (6): 66-69. (in Chinese)
[11] 钟顺时. 微带天线理论与应用[M]. 西安:西安电子科技大学出版社, 1991.
[12] 张福顺, 张进民. 天线测量[M]. 西安:西安电子科技大学出版社, 1995.
[13] 陈 曦, 傅 光, 龚书喜, 等. 阵列天线相位中心的计算与分析[J]. 电波科学学报, 2010, 25(2): 330-335.
CHEN Xi, FU Guang, GONG Shuxi, et al. Calculation and analysis of phase center on array antennas[J]. Chinese Journal of Radio Science, 2010, 25(2): 330-335. (in Chinese)
