基于经验模态分解的大地电磁资料人文噪声处理

蔡剑华 ，汤井田，王先春

(1. 湖南文理学院 物理与电子科学系，湖南 常德，415000；2. 中南大学 地球科学与信息物理工程学院，湖南 长沙，410083)

在电磁探测方法中，人文噪声严重地影响了阻抗响应参数的稳定估计。人文噪声由人工电磁场(如电力传输系统、有线广播、电器设备)与电信工程中的电磁辐射以及其他人类活动产生的噪声、车辆运行等造成，其特点是噪声能量大(正常信号的数倍)，频率集中在有限频带内，结果使得估算的视电阻曲线和相位曲线十分发散，难于构造出解释曲线[1]。随着人类活动的增强，这类噪声的影响越来越大。大量研究人员对去噪进行了研究，提出了诸如小波变换、高阶统计量等一系列方法[2-5]。在此，本文作者把最新发展的经验模态分解应用到大地电磁资料的人文噪声处理中，对实测大地电磁信号中几种常见的人文干扰进行消噪处理，讨论其去噪的方法和效果。

1 经验模态分解

经验模态分解又叫Huang变换。它将信号分解为含有不同时间尺度且满足以下 2个定义条件的 1组IMF(Intrinsic mode function )[6]：(1) 对于一列数据，极值点和过零点数目必须相等或至多相差 1点；(2) 在任意点，由局部极大点和极小点构成的2条包络线的序列平均值为0。每个IMF 可以被认为是信号中固有的1个模态函数。设被分析信号时间序列为X(t)，其分解过程可简要地描述为以下几步[6-8]：

(1) 找出X(t)的所有极大值点和极小值点，将其用三次样条函数分别拟合为原数据序列的上、下包络线。

(2) 上、下包络线的均值序列为平均包络线，用m10表示，将原序列减去m10便可得到一个去掉低频的新序列h10，即h10=X(t)-m10。

(3) 一般地，h10不一定是一个平稳序列，为此，需要重复上述过程。若h10的平均包络线序列为m11，则去除该包络线所代表的低频成分后的序列为h11，即h11=h10-m11。

(4) 重复上述过程，经 k次循环后，使得到的平均包络线序列m1k趋向于0，此时，h1k为第1阶IMF序列，定义为分量c1。

(5) 用X(t)减去c1，得到1个去掉高频成分的新序列r1。再对r1进行分解，便得到第2阶IMF分量c2。如此重复，直到最后1个序列rn不可再被分解时为止，结果可表示为：

因此，原始数据序列X(t)可表示为IMF分量和1个残余项之和：

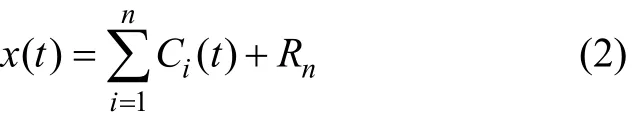
2 EMD消噪算法与步骤

EMD分解出的IMF序列是多通带滤波的结果，信号经过EMD分解后的各阶模态函数能够完全重构，几乎没有能量损失[6]。这样，EMD就可用来减少和消除信号中混杂的噪声，当噪声为1个或多个IMF分量时，直接利用时空滤波器进行消噪[8-10]，如1个包含n个IMF的低通时空滤波器可表示为：

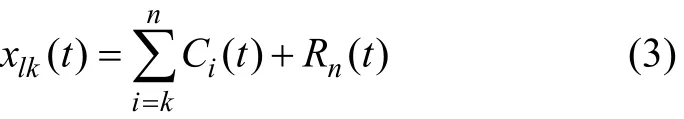
高通时空滤波器为：

若噪声和信号混叠，则可设置硬(或软) 阈值去噪，其过程类似小波变换中的方法[8-9,11]。硬(软)阈值的设定方法描述如下：给定信号x(t)经EMD分解后得到N个IMF, 对每一层IMF选取一合适的阈值, 并用此阈值对Ci进行截断为 ˆiC, 然后进行EMD重构。

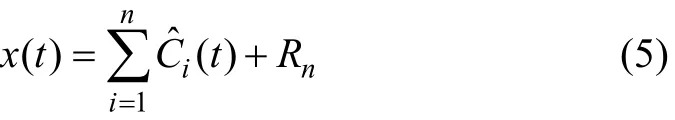
根据Donoho等[9-13]的理论, 给出消除噪声的阈值为：

其中：σi为第i层IMF的噪声水平；Di为第i层IMF的绝对中值偏差，且定义为

第i层IMF的估计 ˆiC，其硬阈值方法为：

软阈值方法为：

综上所述，基于HHT的消噪方法具体步骤如下：

(1) 将含噪信号进行经验模态分解，得到各阶IMF分量。

(2) 根据噪声的不同来源和特征，利用基于EMD的时空滤波器或硬(软)阈值的方法对各IMF分量进行噪声抑制。

(3) 重建处理后的各IMF分量，得到消噪后信号。

3 实测大地电磁参数分析

3.1 脉冲干扰

脉冲干扰是电磁观测中经常遇到的干扰，大多出现在电场中，磁场信号中时常可见到。其特点是振幅常大于正常信号振幅的许多倍，在时间序列上呈正弦阻尼振荡型(采样率较高时)。电场中的脉冲干扰主要来自测点附近介质层中的脉冲型游散电流，这种电流多由测点周围接地用电动力设备的开和关或其负荷的突然改变所造成。电场和磁场中同时出现的脉冲干扰多来自较强的雷电干扰或人类活动中的电磁感应信号[14]。

脉冲干扰的时间特性决定它的频率范围非常宽，若在它进入测量仪器的滤波环节前未被足够抑制，则它对记录资料的影响就会出现在仪器的整个通带内，影响所有频率的观测。图1所示为脉冲干扰的抑制效果。其中，图1(a)所示为1个典型受脉冲噪声影响的电场信号，经计算，在48，97，150，200和320 ms采样点上可以看到明显的脉冲信号，强度上为正常信号的几倍甚至几十倍，最大3.485 V，最小-3.436 V，而均值只有0.245 V，能量为6.102 1×109mV2。这类干扰若出现在电场中，将使计算频率的阻抗幅值严重向上偏移；若出现在磁场中，将使计算频率的阻抗幅值严重向下偏移。

采用 EMD方法对含噪信号进行消噪处理。含噪信号经 EMD分解后自适应地得到 5阶模态函数(图1(b))，每个IMF分量都有不同的振幅和频率，分解顺序是按频率从高至低自适应进行的。imf1表现为信号包含的白噪声，imf2～imf4为优势频率子频带, residual为信号的低频趋势项。根据式(5)～(9)计算各阶IMF序列的阈值, 分别为 97.35，204.18，181.09，143.75和241.20，并用此阈值对各阶分解系数进行修正，最后重构得到消噪后的信号。图 1(c)所示为受脉冲噪声干扰的大地电磁信号经 EMD消噪后的效果图，可见：重构后大地电磁信号的脉冲干扰基本被消除，最大值为885 mV，最小值为-216 mV，均值为184 mV，能量为8.543×108mV2。从改正前后信号能量变化可以估算出噪声能量占总能量的86%左右。

3.2 矩形干扰

当大型电器设备突然启动、关闭或负荷突然改变时, 电道将产生阶跃信号, 一般具有如下形式[14]：

频谱为：

矩形干扰的消除效果见图 2。其中，图 2(a)所示为实测含矩形噪声的MT信号。在150～200和240～300 ms采样点间可见到明显的类似矩形的干扰噪声，强度也非常大，是正常信号的几倍。

采用 EMD方法对含噪信号进行消噪处理。信号经EMD分解后自适应地得到5阶模态函数(图2(b))。从图 2(b)可以看出：矩形干扰信号突变点的位置在imf1～imf4中都能很容易地被检测出来。residual为信号的低频趋势项，其波形形状与原始的的形状较吻合，对应点矩形信号明显，说明矩形噪声的能量主要存在剩余项中。对剩余项强制置零，对 imf1～imf4，按式(5)～(9)计算各阶阈值分别为 235.18，476.42，469.56和127.09。对各阶进行软阈值消噪，最后，重构各阶IMF得到消噪后的信号，图2(c)所示为受干扰的大地电磁信号经 EMD消噪后的效果图。从图 2(c)可以看出：去噪后的信号矩形形状消失，信号变得平稳，近似均值为0、方差为1的平稳随机过程。

图1 脉冲干扰的抑制Fig.1 Suppression of impulse jamming

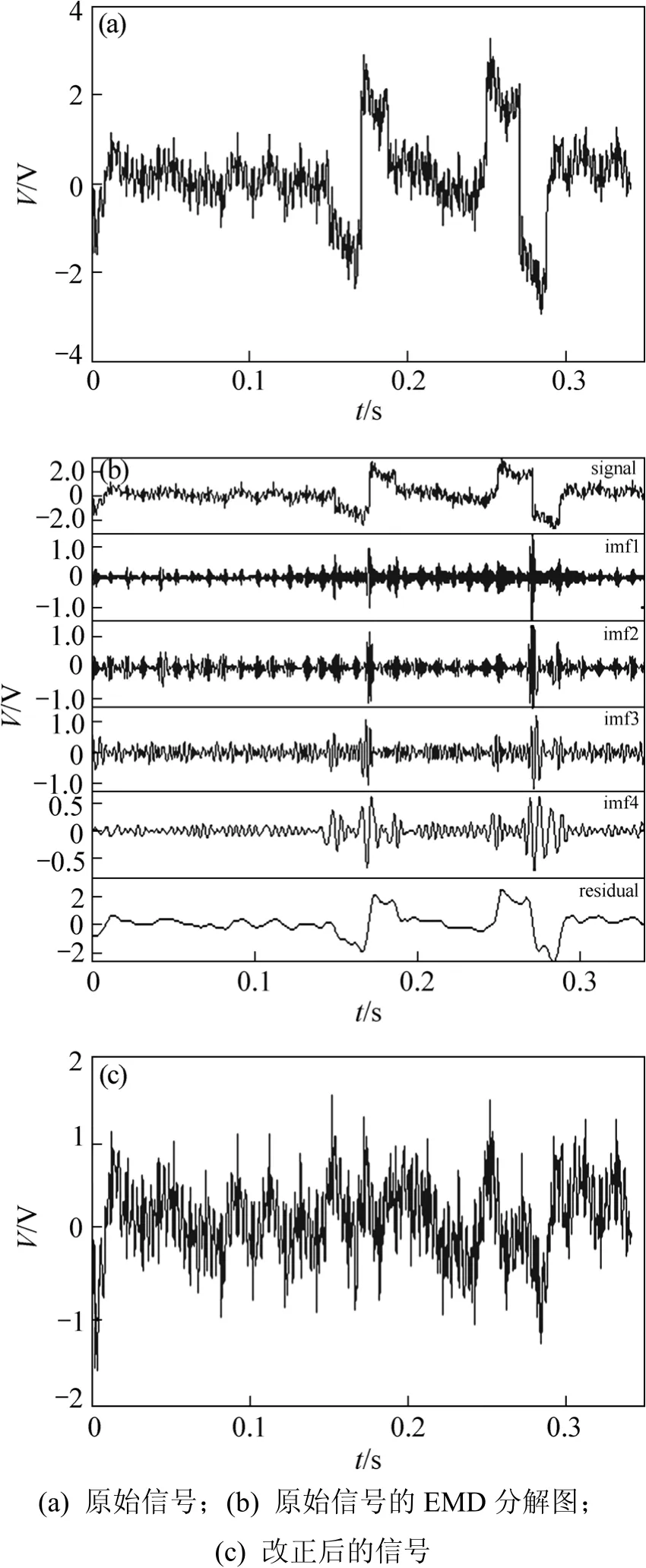
图2 矩形干扰的消除Fig.2 Elimination of rectangle disturbing

3.3 周期正弦噪声

周期正弦噪声往往由观测点附近高压线或其他电器设施产生，由于强度大，在时间序列主要表现为正弦波的形式，它几乎完全掩盖了电磁信号，形成似等振幅的50 Hz噪声干扰。周期正弦噪声的改正效果见图3。其中，图3(a)所示为典型的正弦波干扰，通常具有如下表达形式[15]：

图3 周期正弦噪声的改正Fig.3 Correction of sine wave noise

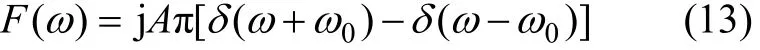
从图 3(a)可以看出：在强正弦噪声干扰下，天然电磁场信号被掩盖，在时间序列上很难识别出天然电磁信号的存在。信号的统计场参量最大值为2.109 22 V，最小值-2.553 752 V，而均值为-0.182 212 V，能量为3.715×109mV2。由于极化方向的原因，这类干

其Fourier变换形式为：扰可能在某个方向上强度较大，在另一个方向上强度较小，对单一主频的噪声往往只对其主频和谐波频率上的阻抗计算产生较大的影响。

采用 EMD方法对含噪信号进行消噪处理, 信号经EMD分解后自适应地得到6阶模态函数(图3(b))。从图3(b)可以看出：第4阶IMF表现为规整的50 Hz正弦波，且幅值很大；第5阶IMF为其谐波，说明正弦噪声主要存在第4阶IMF中。对第4和第5阶IMF强制置零，最后重构得到消噪后的信号。图 3(c)所示为受周期正弦噪声干扰的大地电磁信号经 EMD消噪后的效果图。消噪后信号的统计场参量最大值为1.262 089 V，最小值-1.583 672 V，而均值只有-0.139 708 V，能量为8.052×108mV2，噪声能量占总能量的 78.3%。可见：改正后信号显得较为平稳，看不到周期波形，突出了被噪声掩盖的有用信息。显然，EMD得到的IMF序列为噪声识别和弱信号的提取提供了条件。

4 结论

(1) 大地电磁场具有很宽的频率范围，极易受到各种人文噪声的污染，且随着经济的发展日趋严重，导致大地电磁观测资料质量明显下降。因此，抑制噪声、提高大地电磁数据的质量是MT数据处理的重要任务。

(2) EMD分解为信号的去噪提供了一条良好的途径，其分解出来的IMF序列是多通带滤波的结果，且可以完全重构。据此，可以根据噪声的特征构造时空滤波器或采用硬(软)阈值的方法对大地电磁信号进行消噪处理。

(3) 所提出的噪声抑制方法能有效消除包含在大地电磁信号中的人文干扰，改善受干扰数据的质量，为进一步估算功率谱估计和阻抗奠定了良好的基础。

[1] 孙洁, 晋光文, 白登海, 等. 大地电磁测深资料的噪声干扰[J].物探与化探, 2000, 24(2): 119-128.SUN Jie, JIN Guang-wen, BAI Deng-hai, et al. The noise interference of magnetotelluric sounding data[J]. Geophysical and Geochemical Exploration, 2000, 24(2): 119-128.

[2] Trad D O, Travassos J M. Wavelet filtering of magnetotelluric data[J]. Geophysics, 2000, 65(2): 482-491.

[3] 王书明, 王家映. 高阶统计量在大地电磁测深数据处理中的应用研究[J]. 地球物理学报, 2004, 47(4): 928-934.WANG Shu-ming, WANG Jia-ying. Application of higher-order statistics in magnetotelluric data processing[J]. Chinese J Geophys, 2004, 47(4): 928-934.

[4] 林君, 项葵葵, 朱宝龙, 等. MT信号现场处理的实现技术研究[J]. 数据采集与处理, 1997, 12(1): 52-55.LIN Jun, XIANG Kui-kui, ZHU Bao-long, et al. Study on implementation of MT signal processing in situ[J]. Journal of Data Acquisition & Processing, 1997, 12(1): 52-55.

[5] 汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2): 603-610.TANG Jing-tian, HUA Xi-rui, CAO Zhe-ming, et al.Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J Geophys, 2008,51(2): 603-610.

[6] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society of London, 1998, A454: 903-995.

[7] 蔡剑华, 汤井田, 龚玉蓉. 大地电磁测深数据的时频分析[J].地质与勘探, 2009, 45(4): 462-467.CAI Jian-hua, TANG Jing-tian, GONG Yu-rong. Time-frequency analysis of magnetotelluric sounding data[J]. Geology and Prospecting, 2009, 45(4): 462-467.

[8] Bradley M B, Camelia K. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data[J]. Geophysics, 2007, 72(3): H29-H37.

[9] Donoho D L, Johnstone I. Wavelet shrinkage: Asymptopia?[J]Journal of Royal Statistical Society, 1995, 57(2): 301-369.

[10] Rong J, Hong Y. Studies of spectral properties of short genes using the wavelet subspace Hilbert-Huang transform(WSHHT)[J]. Physica A, 2008, 38(7): 4223-4247.

[11] Coca D, Billings S A. Continuous-time system identification for linear and nonlinear systems using wavelet decompositions[J].International Journal of Bifurcation and Chaos, 1997, 32(1):87-96.

[12] 李夕兵, 张义平, 左宇军, 等. 岩石爆破振动信号的 EMD 滤波与消噪[J]. 中南大学学报: 自然科学版, 2006, 37(1):150-154.LI Xi-bin, ZHANG Yi-ping, ZUO Yu-jun, et al. Filtering and de-noising of rock blasting vibration signal with EMD[J].Journal of Central South University: Science and Technology,2006, 37(1): 150-154.

[13] Yue H Y, Guo H D. A SAR interferogram filter based on the empirical mode decomposition method[C]//Proceedings of Geoscience and Remote Sensing Symposium. Nanjing: IEEE,2001: 2060-2063.

[14] 严家斌, 刘贵忠, 柳建新. 小波变换在天然电磁场信号时间序列处理中的应用[J]. 地质与勘探, 2008, 44(3): 75-78.YAN Jia-bin, LIU Gui-zhong, LIU Jian-xin, Application of wavelet transform in processing nature electromagnetic field time series[J]. Geology and Prospecting, 2008, 44(3): 75-78.