无碴轨道预应力混凝土梁长期变形及影响因素

叶梅新，曹建安，侯文崎，肖佳

(中南大学 土木建筑学院，湖南 长沙，410075)

无碴轨道因轨道稳定性、刚度均匀性和耐久性好、线路平顺性高、维修工作量小等突出优点，在国内外高速铁路中得到广泛应用[1-2]。有碴轨道可通过道碴调节轨道线形，而无碴轨道只能通过调整扣件保证轨道线形，且扣件的可调节量非常有限[3-4]。对于桥上无碴轨道，桥梁结构受活载作用引起的弹性变形和恒载作用引起的长期变形都会直接影响到轨道结构的受力和线路平顺性，从而危及行车安全。因此，为保证桥上无碴轨道线路平顺性，必须研究并有效控制无碴轨道预应力混凝土桥梁后期变形(后期变形指二期恒载施加完成后桥梁的变形)。石现峰等[5]认为，预应力混凝土梁桥后期变形主要由混凝土徐变引起。混凝土徐变变形影响因素复杂，现行各种规范对混凝土徐变系数的定义和计算方法差异较大。徐变计算理论和计算软件较多，但所得计算结果差别很大，且与实测结果不太吻合[6-7]。这些都给预应力混凝土桥梁后期变形控制带来很大困难。与简支梁桥相比，预应力混凝土连续刚构桥的收缩徐变规律更加复杂，特别是悬臂施工桥梁，其徐变规律和徐变的离散性很大[8-9]。我国新建铁路广珠(广州—珠海)城际轨道交通全线采用无碴轨道。其中，容桂水道特大桥是1座预应力混凝土连续刚构桥，跨度为(108+2×185+115) m，为目前我国跨度最大的无碴轨道预应力混凝土桥梁。该桥主梁采用C60混凝土，单箱单室直腹板变截面，三向预应力体系，悬臂浇筑施工。桥梁后期变形控制是该桥设计、施工急需解决的关键问题之一。本文按照容桂水道桥实桥配比，在实验室条件下的混凝土试块徐变试验基础上，确定该桥后期变形计算方法。根据全桥后期变形计算结果，按照边跨的应力水平设计，制作3根后张法预应力混凝土简支试验梁，通过长达762 d的试验观测，研究试验梁后期变形规律及其影响因素，并提出有效控制预应力混凝土梁后期变形的建议措施。

1 徐变变形计算方法

混凝土徐变变形是指在持续荷载作用下，混凝土结构变形随时间不断增加的现象，通常采用徐变系数来描述。国内外主要混凝土规范[10-15]都以混凝土龄期28 d时的弹性应变为基准来定义徐变系数，如欧洲规范 CEB/FIP(1990)[15]、中国铁路规范 TB10002.3—2005[10](下称中铁05规范)和中国公路规范JTG D62—2004[13](下称中交04规范)等。各种规范都规定了各自适用的桥梁跨度范围。容桂水道特大桥的跨度已远超过这些规范所规定的跨度范围，需要根据实测徐变系数确定适用规范。

为此，本文按照实桥混凝土配比(见表 1)制作 1组共3个C60高性能混凝土棱柱体试件，测试了徐变系数。试件尺寸(长×宽×高)为100 mm×100 mm×400 mm，试验环境相对湿度为60%，加载龄期为28 d。实测徐变系数取3个试件的平均值。

表1 容桂水道桥实桥C60高性能耐久性混凝土配合比Table 1 Mix proportion of C60 high performance concrete of RGB kg/m3

图1所示为混凝土徐变系数实测值与按各种规范所得计算值的对比结果。由图1可见：按各种规范计算所得徐变系数均大于实测徐变系数；按中铁05规范计算所得徐变系数与实测值差别最大，中交04规范和CEB/FIP(1990)两者的计算值较接近，与实测值差别较小。其中，中交04规范混凝土徐变系数计算考虑了混凝土强度等级的影响，强度等级越高，徐变系数越小；而中铁05规范则没有考虑混凝土强度等级的影响。

经综合比较，本文徐变变形计算采用中交 04规范。计算结果表明：容桂水道桥后期徐变变形在边跨上拱，中跨靠近边跨部分下挠，靠近中墩部分上拱，且边跨的变形幅度大于中跨的变形幅度，见图2。

图1 徐变系数实测值与计算值对比Fig.1 Comparison of tested and calculated values of creep coefficient for concrete

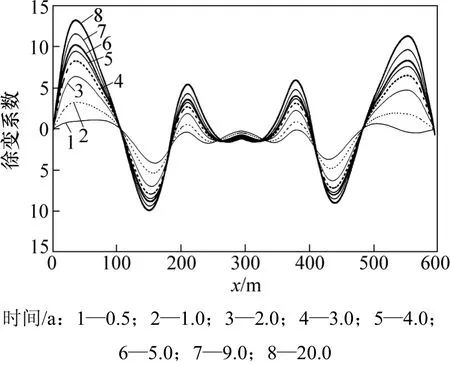
图2 容桂水道桥后期变形曲线Fig.2 Long term deformation curves of Ronggui bridge

2 预应力混凝土梁长期变形试验

2.1 试验梁设计

本试验模拟容桂水道桥变形较大边跨的后期徐变变形情况和受力状态。考虑实验室场地、预应力筋位置、张拉控制应力、预应力加载龄期、堆载(模拟二期恒载)龄期(分6种)以及堆载大小等因素，本文共设计了5大类共30根等截面简支预应力混凝土试验梁。通过有限元对比分析，并考虑到试验梁后期变形、材料用量、堆载实现难易程度等因素，经反复筛选，最终确定3根试验梁，记为Ⅰ，Ⅱ和Ⅲ。这3根试验梁的几何尺寸(长×宽×高)均为10.0 m×0.3 m×0.4 m，普通钢筋配筋率和预应力钢束的布置也相同，但预应力张拉与二期恒载加载时的混凝土龄期不同。其中：Ⅰ和Ⅱ号梁应力张拉龄期为7 d，Ⅲ号梁为30 d；Ⅰ号梁堆载龄期为28 d，Ⅱ和Ⅲ号梁为60 d。图3所示为试验梁预应力钢束布置图。

2.2 试验梁制作、加载和测试

表2所示为实测混凝土强度和弹性模量。在满足构造要求的前提下，试验梁纵向普通钢筋配筋率与实桥的相同，为0.05%；预应力钢筋采用无黏结钢绞线，抗拉强度标准值fpk=1.86 GPa，单根张拉力为188 kN。二期恒载采用堆载实现。

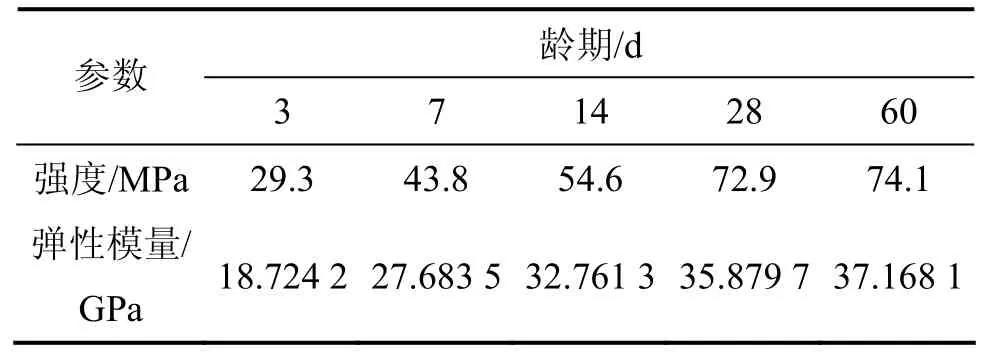
表2 实测试验梁混凝土强度和弹性模量Table 2 Tested cubic strength and elastic modulus of experimental beams

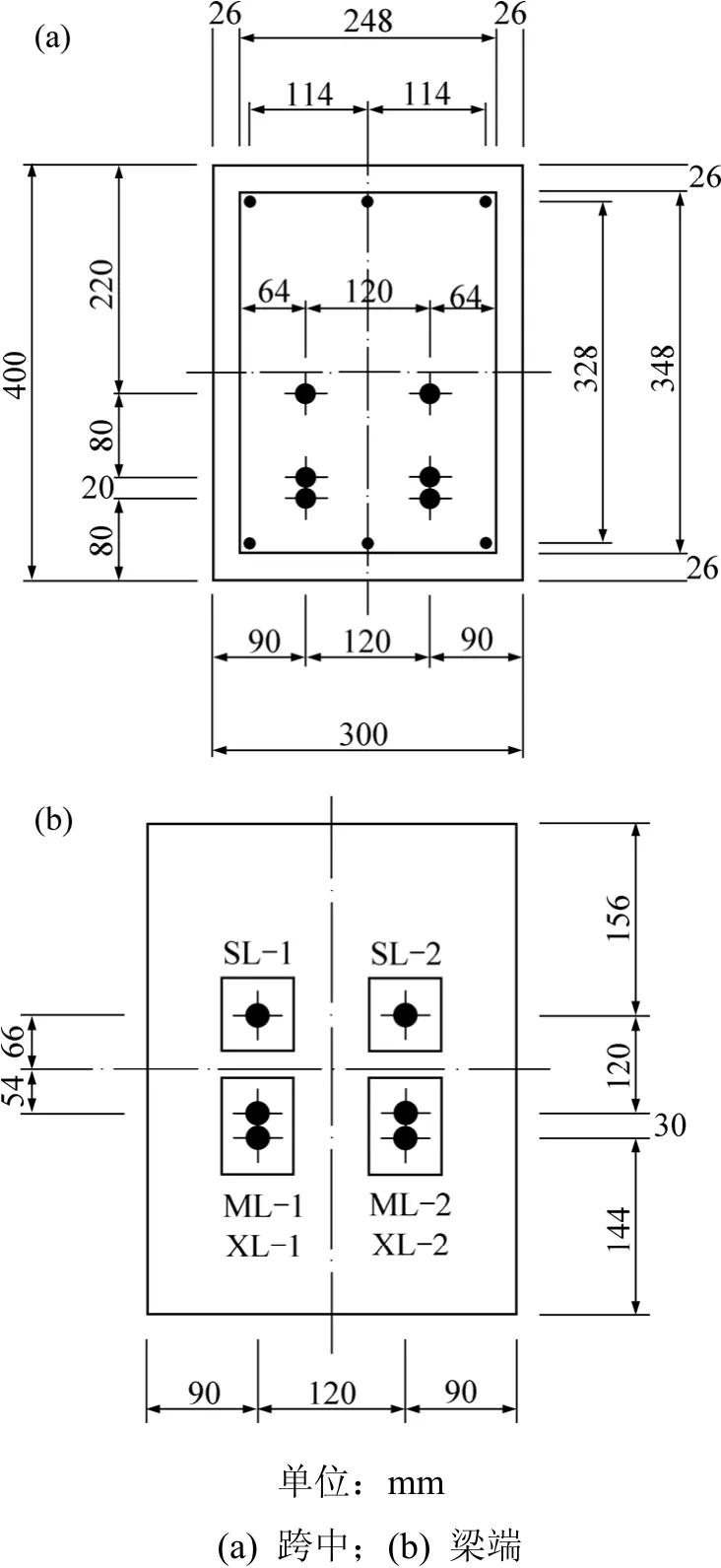
图3 跨中及梁端预应力筋布置图Fig.3 Pre-stressed tendons arrangement in middle span and beam end

整个试验历时762 d，主要测试内容包括：

(1) 试验梁跨中变形，采用千分表测量，测点布置见图4。

(2) 混凝土的应变，采用表面式应变计测量；

(3) 预应力钢束张拉力损失，采用穿心式压力传感器测量；

图4 各试验梁千分表布置图Fig.4 Arrangement of dial gauges on test beams

(4) 试验室环境湿度、温度等，分别采用温度计和湿度计测量。

3 长期试验结果及分析

试验结果表明：各试验梁的位移、应变和预应力钢束内力的实测值均小于计算值，且实测值与计算值变化规律基本相同。

3.1 环境温度、湿度变化规律

试验期间，环境温度和湿度随天气和季节的变化波动较大，温度变化范围为 5～36 ℃，夏季最高温度为36 ℃，冬季最低气温为5 ℃，平均温度约为20 ℃；湿度变化范围为50%～100%，冬季湿度普遍较高，平均湿度约为75%。见图5。

3.2 试验梁跨中位移变化规律

在试验观测期间，各试验梁跨中均发生上拱变形。预应力张拉完成后，各试验梁跨中位移急剧上移，堆载后产生突降，然后继续发展，但变化缓慢，见表 3和图 6～8。图 6(a)～8(a)中：曲线以试验梁预应力张拉完成后的线形为基准。

堆载后的后期变形期间，前185 d内各试验梁跨中上拱发展较快，平均约占总后期变形的75%；之后的500余d内各试验梁跨中上拱发展趋于平缓，平均约占总后期变形的25%。见表3和图6(b)～8(b)，图中曲线以堆载后试验梁的线形为基准。

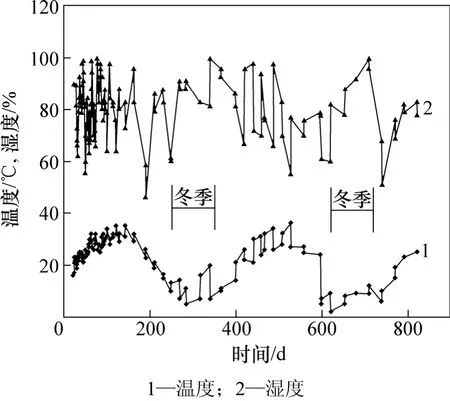
图5 试验室环境温度和湿度时程曲线Fig.5 Time history curves of ambient temperature and humidity in laboratory

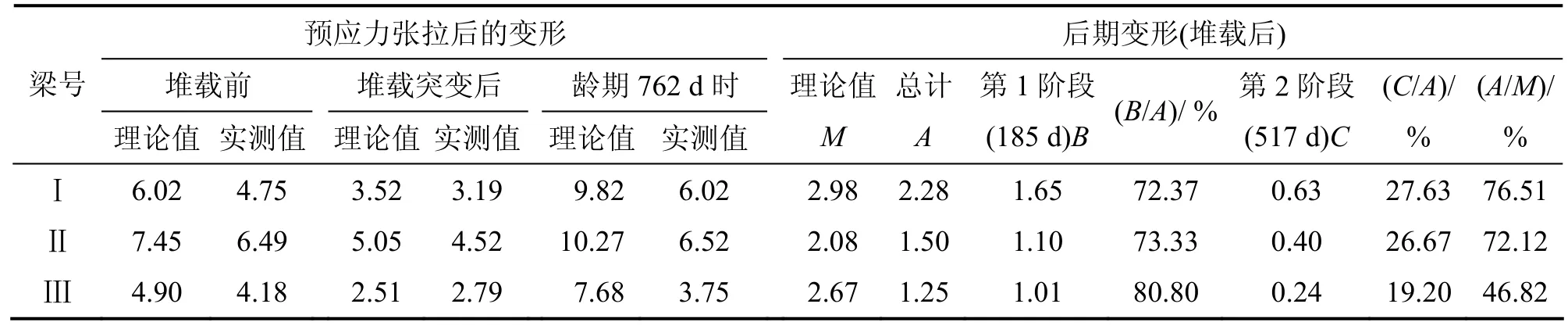
表3 不同阶段各试验梁跨中变形理论值与实测值的对比Table 3 Comparison of tested and calculated deformation in mid-span of test beams

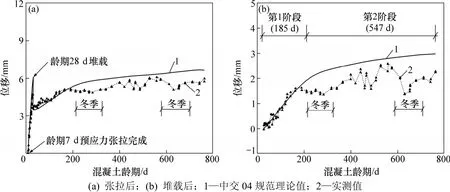
图6 Ⅰ梁预应力张拉后和堆载后跨中后期变形位移时程曲线Fig.6 Displacement-time curves in mid-span of beam Ⅰ after pre-stress tension and after surface loading

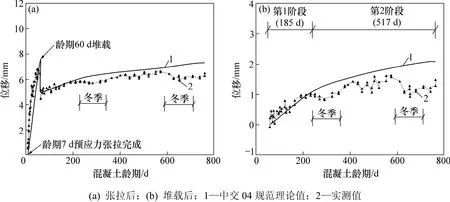
图7 Ⅱ梁预应力张拉后和堆载后跨中后期变形位移时程曲线Fig.7 Displacement-time curves in mid-span of beam Ⅱ after pre-stress tension and after surface loading

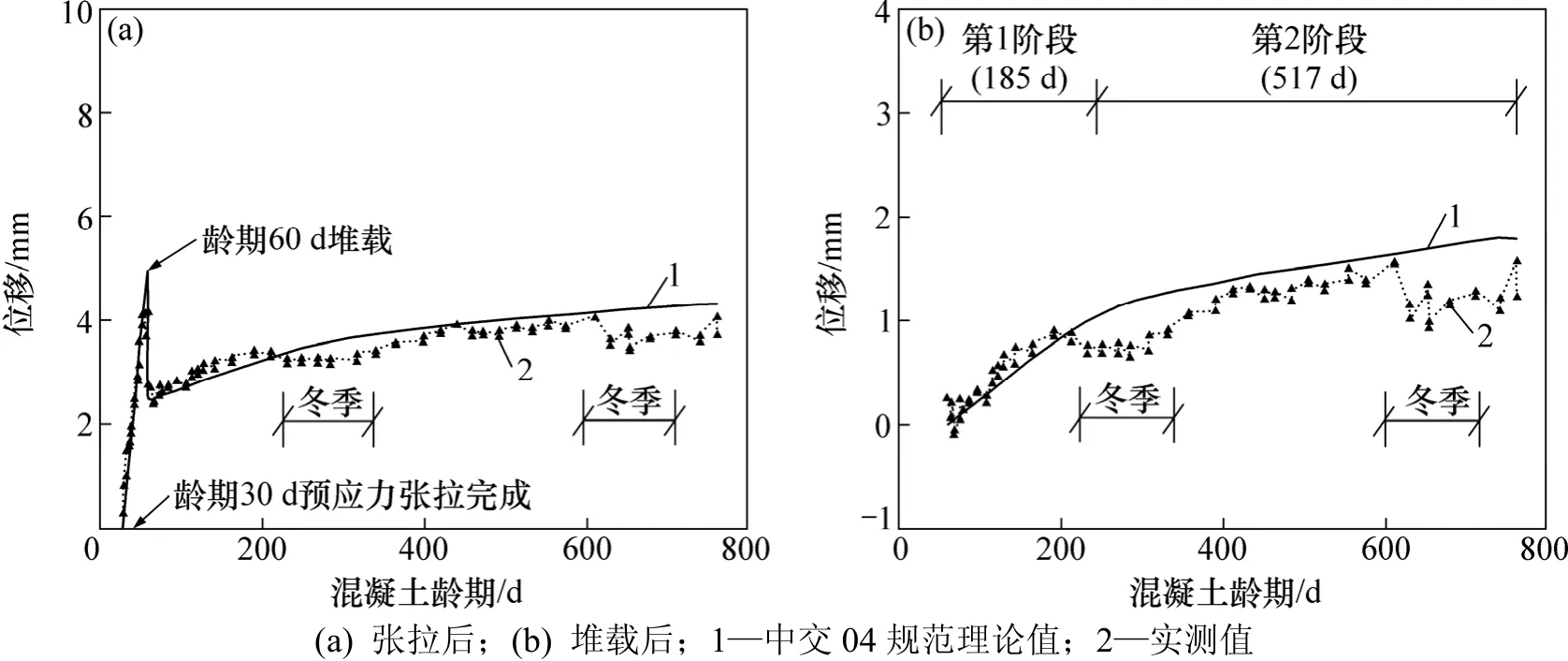
图8 Ⅲ梁预应力张拉后和堆载后跨中后期变形位移时程曲线Fig.8 Displacement-time curves in mid-span of beam Ⅲ after pre-stress tension and after surface loading

3.3 试验梁跨中截面混凝土表面应变变化规律

在试验期间，各试验梁跨中截面混凝土下表面应变的发展规律与跨中上拱变形的发展规律相吻合，均是在预应力张拉完成后迅速增大，堆载后产生突降，之后继续发展，但速度缓慢；混凝土龄期达到 400 d以后，各试验梁混凝土表面应变基本稳定，到龄期762 d时基本没有增大。冬季由于温度降低和湿度增大，各试验梁混凝土表面应变均明显减小，随着温度回升，混凝土表面应变有短暂突增，随即趋于稳定，见图9。试验结果表明：Ⅰ，Ⅱ和Ⅲ号试验梁堆载后的后期应变分别占762 d总应变的31.6%，22.5%，28.1%。见表4。

3.4 预应力钢束内力变化规律

在762 d的试验中，各试验梁实测预应力钢束内力的损失很小，最大不超过8.63%，见表5。堆载前，各试验梁预应力钢束拉力损失速率相对较大，堆载后逐渐趋于平缓，特别是在混凝土龄期500 d以后，预应力钢束拉力的损失速率很小。以Ⅰ，Ⅱ和Ⅲ号试验梁的SL1钢束为例，预应力张拉后到混凝土龄期762 d期间，钢束SL1预应力损失率分别为 8.25%，8.07%和 6.54%；堆载后到混凝土龄期 762天(后期变形)期间，SL1的预应力损失率分别为 4.38%，3.51%和2.70%。后者最多不超过前者的 53%。这说明预应力混凝土梁的后期变形主要还是由混凝土徐变引起，预应力损失引起的变形很小。

表4 不同阶段各试验梁跨中截面混凝土下表面应变Table 4 Concrete strain on bottom surface of mid-span section of test beams in different periods µε

图9 Ⅰ梁预应力张拉后和堆载后跨中混凝土下表面总应变Fig.9 Strain-time curves on bottom concrete surface in mid-span of beamⅠ after pre-stress tension and after surface loading

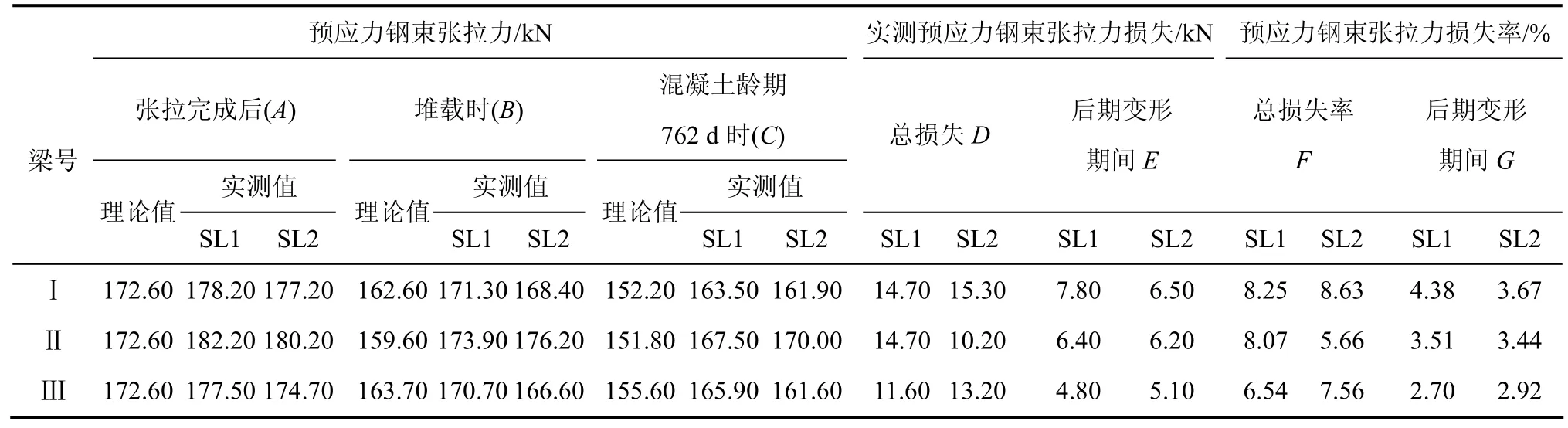
表5 试验梁预应力钢束拉力损失对比Table 5 Comparison of loss of pre-stress of test beams

4 预应力混凝土梁后期徐变影响因素分析

4.1 环境温度和湿度的影响

试验结果表明：低温度、高湿度环境能够有效减小预应力混凝土梁的后期徐变变形。从图5～9可见：

(1) 混凝土龄期180～240 d时段内，环境湿度相对稳定在82%左右，温度下降约19 ℃，各试验梁跨中位移和混凝土下表面应变均明显减小。其中，Ⅰ，Ⅱ和Ⅲ号试验梁堆载后的跨中位移分别减小 0.177，0.039和0.077 mm，平均减小约8.0%；跨中混凝土下表面应变分别减小了 8.63µε，8.50µε和 8.29µε，平均减小约8.5%。

(2) 混凝土龄期360～400 d时段内，环境温度相对稳定在11 ℃左右，湿度降低约15%；各试验梁跨中位移和混凝土下表面应变均明显增大；其中，Ⅰ，Ⅱ和Ⅲ试验梁堆载后的跨中位移分别增大 0.160，0.234和0.063 mm，平均增大约11.6%；跨中混凝土下表面应变分别增大 18.07µε，9.25µε和 11.78µε，平均增大约5.2%。

因此，在实际工程中特别是高温环境下，预应力混凝土桥梁的保湿养护对其后期变形控制十分重要。

4.2 预应力钢束张拉龄期的影响

预应力钢束张拉龄期越早，预应力混凝土梁的后期徐变变形越大，适当延长预应力加载龄期可有效减小预应力混凝土桥梁的后期变形。

试验梁Ⅱ和Ⅲ的堆载龄期相同，但预应力钢束张拉龄期不同。其中，试验梁Ⅱ预应力钢束张拉龄期为7 d，试验梁Ⅲ为30 d，比前者晚23 d。表3所示结果表明：试验梁Ⅱ和Ⅲ跨中处的后期变形分别为1.50和1.25 mm，后者比前者减小了约16.51%。因此，在实际工程中，可采用预留部分后张钢束和设计体外束的措施以控制桥梁后期徐变变形。

4.3 堆载龄期的影响

二期恒载的加载龄期越早，预应力混凝土梁的后期徐变变形越大，适当推迟二期恒载加载时间可有效减小预应力混凝土桥梁的后期徐变变形。

试验梁Ⅰ和Ⅱ的预应力钢束张拉龄期相同，但堆载龄期不同。其中，试验梁Ⅰ堆载龄期为28 d，试验梁Ⅱ堆载龄期为60 d，比前者推迟了32 d。表3、图8(b)、图 9(b)所示试果表明：试验梁Ⅰ和Ⅱ跨中处的后期变形分别为2.28和1.50 mm，后者比前者减小约34.27%。在实际工程中，可适当延长铺轨时间以有效控制桥梁后期徐变变形，考虑到桥梁施工和运营成本，一般延长半年铺轨为宜。

5 结论

(1) 按照各种规范计算所得混凝土徐变系数差异较大，且均大于实测徐变系数。按中交04规范计算所得徐变系数较按中铁05规范所得值更接近实测值，且考虑了混凝土强度等级对徐变系数的影响。因此，本文采用中交04规范计算C60高性能混凝土结构徐变变形。

(2) 预应力混凝土梁的位移和应变都是在预应力张拉完成后急剧增大，堆载后产生突降，之后继续发展，但速度缓慢。堆载后的后期变形期间，在前185 d内各试验梁的跨中上拱变形平均约占总后期变形的75%；在之后的500余d内，跨中上拱变形平均约占总后期变形的25%；混凝土表面应变在400 d时基本稳定，之后仅随环境温度、湿度的变化有所波动。

(3) 预应力混凝土梁预应力钢束内力的损失很小，最多不超过 8.63%。因此，预应力混凝土梁的后期变形主要是混凝土徐变引起的，预应力损失引起的变形很小。

(4) 当预应力混凝土梁的截面尺寸、预应力钢束布置、配筋率相同时，环境温度和湿度、预应力加载龄期、二期恒载加载龄期等是结构后期徐变变形的主要影响因素。在实际工程中，在高湿度、低温度的混凝土养护环境下，适当延长预应力张拉龄期，预留后张钢束和设计体外备张钢束，并适当延长铺轨时间等都是控制预应力混凝土桥梁后期徐变变形的有效措施。

[1] 朱高明. 国内外无砟轨道的研究与应用综述[J]. 铁道工程学报, 2008, 118(7): 28-30.ZHU Gao-ming. Overall comments on study and application of ballastless track at home and abroad[J]. Journal of Railway Engineering Society, 2008, 118(7): 28-30.

[2] 沈东升. 客运专线无砟轨道的技术应用与发展[J]. 中国铁路,2009(10): 11-14 SHEN Dong-sheng. Technical application and development of ballastless track on passenger express railway[J]. Chinese Railways, 2009(10): 11-14.

[3] 江成, 范佳, 王继军. 高速铁路无砟轨道设计关键技术[J]. 中国铁道科学, 2004, 25(2): 42-47.JIANG Cheng, FAN Jia, WANG Ji-jun. Key techniques of ballastless track design on high-speed railway[J]. China Railway Science, 2004, 25(2): 42-47.

[4] 向俊, 曹晔, 刘保钢, 等. 客运专线板式无碴轨道动力设计参数[J]. 中南大学学报: 自然科学版, 2007, 38(5): 981-986.XIANG Jun, CAO Ye, LIU Bao-gang, et al. Dynamic parameters of slab track of passenger transport line[J]. Journal of Central South University: Since and Technology, 2007, 38(5): 981-986.

[5] 石现峰, 王澜, 万家. 无砟轨道混凝土桥梁的徐变变形研究[J]. 石家庄铁道学院学报, 2007, 20(1): 61-63.SHI Xian-feng, WANG Lan, WAN Jia. Analysis of creep deformation of concrete bridge with ballastless track[J]. Journal of Shijiazhuang Railway Institute, 2007, 20(1): 61-63.

[6] 林波. 混凝土收缩徐变及其效应的计算分析和试验研究[D].南京: 东南大学土木工程学院, 2006: 57-67.LIN Bo. Experimental and theoretical analysis of shrinkage and creep effects of concrete[D]. Nanjing: South East University.Civil Engineering Institute, 2006: 57-67.

[7] 刘杰. 预应力混凝土结构徐变效应的计算理论及计算方法研究[D]. 长沙: 中南大学土木建筑学院, 2009: 27-36.LIU Jie. Study on the theory and calculation methods of creep effect of pre-stressed concrete structure[D]. Changsha: Central South University. School of Civil Engineering and Architecture,2009: 27-36.

[8] 何义斌. 大跨度无砟轨道连续梁桥后期徐变变形研究[J]. 铁道学报, 2008, 30(4): 120-124.HE Yi-bin. Study on post creep deformation of long-span concrete continuous bridge with ballastless tracks[J]. Journal of the China Railway Society, 2008, 30(4):120-124.

[9] 罗许国, 钟新谷, 戴公连. 高性能混凝土梁长期变形性能试验研究[J]. 铁道科学与工程学报, 2005, 2(4): 45-49.LOU Xu-guo, ZHONG Xin-gu, DAI Gong-lian. Experimental study on the long term deformations in high performance concrete beam[J]. Journal of Railway Science and Engineering,2005, 2(4): 45-49

[10] TB l0002.3—2005. 铁路桥涵设计基本规范[S].TB l0002.1—2005. Fundamental norms for railway bridge design[S].

[11] TB l0002.3—99. 铁路桥涵钢筋混凝土及预应力混凝土结构设计规范[S].TB l0002.3—99. Design codes for railway reinforced concrete and pre-stressed concrete bridge structures[S].

[12] JTJ 023—85. 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTJ 023—85. Design codes for highway reinforced concrete and pre-stressed concrete bridge structures[S].

[13] JTG D62—2004. 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTG D62—2004. Design codes for highway reinforced concrete and pre-stressed concrete bridge structures[S].

[14] CEB-FIP (1978). CEB-FIP model code for concrete structures[S].

[15] CEB-FIP (1990). CEB-FIP model code for concrete structures[S].