简支转连续桥梁支点截面应力测试与研究
2022-05-05郭东升辽宁省交通规划设计院有限责任公司辽宁沈阳110166
郭东升 (辽宁省交通规划设计院有限责任公司,辽宁 沈阳 110166)
0 引言
简支转连续梁桥以其行车舒适良好、梁体预制安装施工方便、跨越能力大等优点,在我国中小跨径混凝土桥梁中得到广泛应用,且占相当大的比重,它兼具了简支梁桥和连续梁桥的优点[1~3]。连续梁桥墩顶负弯矩区在施工过程中及成桥以后容易出现过大的拉应力继而产生裂缝,为了控制该区域拉应力避免横向裂缝的产生,会在连续梁桥负弯矩区设计负弯矩钢束[4]。而这个区域以支点截面受力最大,测试和分析支点截面的应力状况能够反映整个区域的受力是否安全、负弯矩钢束设计是否合理、张拉是否完全,进而为类似桥梁的设计、施工提供一个参考。
本文以某高速公路连接线上3×40m简支转连续T梁桥为依托,根据桥梁实际情况提出实桥试验方案并进行跟踪测试,运用有限元软件Midas Civil建立试验桥分析模型,将实测数据和有限元模型数据进行对比分析,讨论张拉负弯矩钢束过程中的支点截面的应力变化状态。
1 基本概况
1.1 桥梁概况
本桥为某高速公路连接线上K45+191处的10×40m简支转连续T梁桥,试验段为其最后一联(8、9、10三跨)。桥梁跨径40m,桥宽12.25m,横截面由5片梁高2.5m主梁组成,主梁采用C50混凝土,试验段立面图见图1。每片主梁配置6束每束5根,15.24mm低松弛钢筋,张拉控制应力1395MPa,依次张拉9#墩顶和8#墩顶负弯矩束,张拉顺序为T3左®T3右®T2左®T2右®T1左®T1右(左、右以小桩号向大桩号方向确定),负弯矩钢束布置见图2。

图1 试验段立面图(单位:cm)
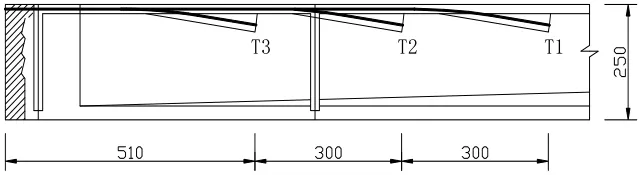
图2 负弯矩钢束布置图(单位:cm)
1.2 试验概况
在试验段桥梁施工过程中,将振弦式应变计埋设于T梁支点截面,基于桥梁横截面为5片T梁,选取4号梁为试验梁。在浇筑墩顶湿接混凝土前,于AA、B-B截面0.21m、1.25m、2.4m高度处预埋混凝土应变计,位置如图3所示,待墩顶混凝土达到设计强度按顺序对负弯矩钢束进行张拉,在张拉过程中进行数据采集并做好记录[5][6],应变计现场布置位置见图4。

图3 支点截面应变计测点布置图(单位cm)

图4 应变计现场布置
2 模型建立与对比验证
2.1 有限元模型建立
运用有限元软件Midas Civil建立试验段三跨简支转连续预应力混凝土T型梁桥模型,以实际形状布置负弯矩钢束并按现场的预应力钢束张拉顺序划分相应施工阶段。建模方法采用梁格法,纵向5片主梁采用空间梁单元模拟,通过主梁截面尺寸计算纵向梁格刚度,为模拟纵梁之间的横向联系,横隔板按照实际位置及尺寸建模,计算其真实的自重和刚度,其他位置按实际主梁翼缘板刚度建立虚拟横梁,虚拟横梁不计自重,中横梁位置进行单元加密以保证其刚度。主梁临时支座用一般支承模拟,结构除考虑自重外还应有施工荷载、预加力荷载、收缩徐变等[7][8]。张拉阶段桥梁有限元模型见图5。

图5 张拉阶段桥梁有限元模型
2.2 计算值与实测值对比验证
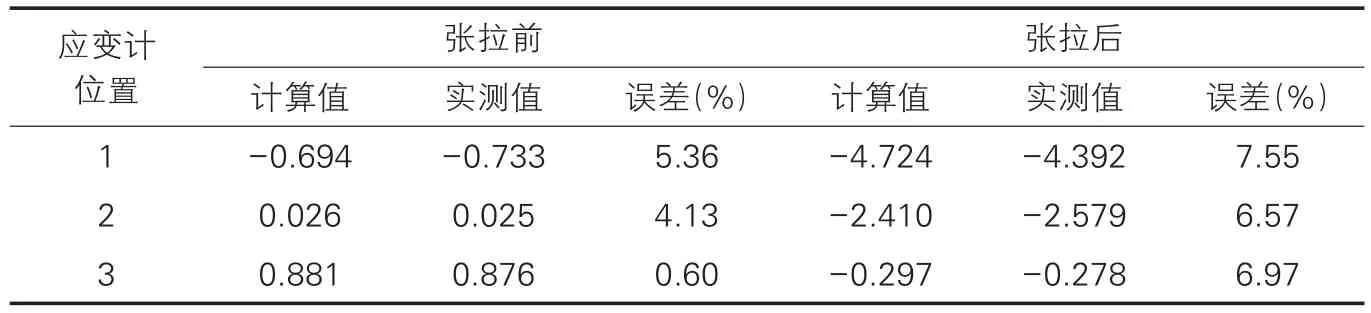
通过Midas Civil有限元模型的计算,对比A-A、B-B截面1、2、3号应变计位置处有限元计算值和现场实测数据,9-10及8-9墩顶负弯矩钢束张拉前后A-A、B-B截面应力对比分别见表1、表2。

张拉前后A-A截面应力对比(单位MPa) 表1
张拉前后B-B截面应力对比(单位MPa) 表2
由表1、表2可以看出有限元模型计算得出的A-A、B-B截面应力值与现场实测数据能够较好的吻合,误差最大值为9.81%,故认为模型建立方法及过程正确、计算结果合理可靠,能够反映结构该部位真实受力情况,可作为分析截面应力的依据[9]。
分析表1数据可知,9#墩顶负弯矩钢束张拉前A-A截面上缘受压下缘受拉,截面应力值较小均小于0.2MPa,张拉后截面处于全截面受压状态,且截面上、下缘压应力有明显增大,说明张拉负弯矩钢束会使支点截面应力发生较大变化。分析表2数据得出张拉8#墩顶负弯矩钢束前,B-B截面同样是上缘受压下缘受拉且截面应力值较小,但大于表1中应力值,是因为此时9-10已经张拉完成,使B-B截面应力变大,张拉完成后,截面承受压应力最大值为4.724MPa,应力沿梁高呈线性变化,A-A、B-B截面钢筋混凝土处于弹性受力阶段,结构受力安全。
3 负弯矩张拉阶段应力分析
3.1 张拉9#墩顶钢束过程截面应力分析
由有限元模型计算出张拉每束钢绞线后 A-A、B-B截面 0.21m、1.25m、2.4m高度处的应力值,用以分析负弯矩钢束张拉过程中支点截面的应力状态,9#墩顶张拉过程中两截面应力的变化过程见图6、图7。
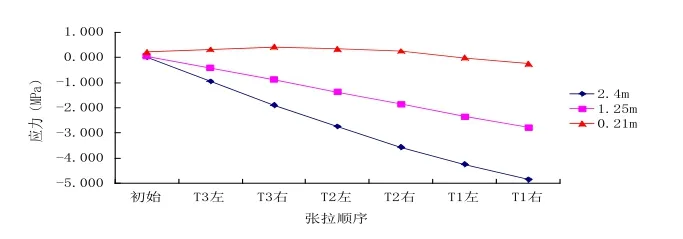
图6 9#墩顶钢束张拉过程A-A截面应力值

图7 9#墩顶钢束张拉过程B-B截面应力值
由图6可以看出,初始A-A全截面受拉但拉应力值较小,最大拉应力为0.213MPa。随着预应力钢束的张拉,截面上缘出现压应力并逐渐增大,从图中可以看出其变化趋势越来越缓,说明从张拉T3钢束到张拉T1对A-A截面应力的影响依次减小。A-A截面1.25m高度处应力同样向压应力方向发展,基本呈直线变化。截面下缘应力在0MPa左右变化,张拉T3拉应力增大,张拉T2、T1向压应力反向变化,张拉钢束对截面应力的影响可分为两部分,一部分是预应力产生的压应力,表现为图中1.25m处变化趋势,另一部分是由于预应力偏心引起弯矩进而使上缘产生压应力、下缘产生拉应力,表现为图中上下缘应力的发展趋势,而T3钢束张拉时第二部分起主导作用,于是截面下缘向拉应力增大,T2、T1张拉时,第一部分影响较大,所以截面下缘应力向压应力方向发展。
由图7可知,B-B截面在初始状态同样全截面受拉,在张拉9#墩顶负弯矩钢束过程中,截面上缘压应力不断增大,但压应力总体较小,最大值达到0.504MPa。截面下缘拉应力会逐渐变大,在钢束张拉完成后会出现0.973MPa的拉应力,图中可以看出,上、下缘应力变化趋势逐渐变陡,说明T1钢束张拉对B-B截面应力的影响更加明显,这是因为T1钢束的锚固点更接近B-B截面。
对比图6、图7可以看出,张拉9#墩顶负弯矩钢束对A-A截面上缘压应力及B-B截面下缘拉应力影响较大,张拉完成后,A-A截面压应力明显大于B-B截面,但最大值为4.849MPa,A-A截面受力安全,此时B-B截面下缘会出现较大的拉应力,所以应该关注8#墩支点处,防止出现裂缝。
3.2 张拉8#墩顶钢束过程截面应力分析
在9#墩顶负弯矩钢束张拉完成后,按照顺序对8#墩顶进行张拉,其过程中A-A、B-B两截面1、2、3号应变计对应位置处的应力变化见图8、图9。

图8 8#墩顶钢束张拉过程A-A截面应力值

图9 8#墩顶钢束张拉过程B-B截面应力值
由图8可以看出,由于通过A-A截面的预应力钢束已经在前一阶段全部张拉完成,所以张拉8#墩顶负弯矩钢束前,A-A截面内存在较大的压应力,在张拉过程中,仍然是截面上缘压应力增大,下缘向拉应力方向发展,但总体变化幅度较小。由图9可知,在此过程中BB截面的压应力有明显增大,由张拉前的0.504MPa增加到最终的5.546MPa,B-B截面下缘拉应力在张拉T3时增大,而张拉T2、T1时减小。
对比图8、图9可得,张拉8#墩顶负弯矩钢束对A-A截面应力影响较小,而对B-B截面影响偏大。张拉完成后,AA、B-B截面应力分布状况接近,均为上缘承受5.5MPa左右压应力,下缘承受0.43MPa左右拉应力,应力大小合理,结构安全,且应力沿梁高线性变化,处于弹性受力阶段。
综上所述,张拉墩顶负弯矩钢束对钢束通过的支点截面应力有明显影响,同时对相邻支点截面有影响,且未张拉钢束的受其影响较大,已张拉钢束受到的影响较小。负弯矩钢束的作用体现在合理设计的负弯矩钢束能够很好地限制支点截面拉应力的产生,进而避免桥面裂缝的出现及张拉完成后的压应力储备为后期承受二期恒载和活载等提供保障,发挥后连续的作用[10~11]。
4 结论
①桥梁在张拉9#、8#墩顶负弯矩钢束过程中,两支点截面上缘应力向压应力方向发展,下缘应力向拉应力发展;张拉完成后,支点截面内存储5.5MPa左右的压应力,为承受后期荷载提供应力储备。
②张拉过程中,T3钢束对负弯矩钢束通过的支点截面应力影响较大,T1钢束对相邻支点截面应力影响较大。
③A-A截面上缘在整个张拉过程中拉应力较小,B-B截面上缘最大拉应力在出现在8#墩顶的T3钢束张拉完成时,为0.973MPa,未超过C50混凝土抗拉设计强度,结构安全。
