考虑徐变恢复的混凝土徐变效应分析

周勇军 丁伟慧 赵煜 李源 吴领领

（1.长安大学旧桥检测与加固技术交通行业重点实验室，西安 710064；2.长安大学公路学院，西安 710064）

徐变是混凝土重要性质之一，其影响不容忽视［1-2］。对于变化应力作用下的徐变，国内外学者从不同角度提出了很多计算方法。文献［3］提出徐变率法可用于复杂结构的徐变计算中，但是该方法认为徐变速率与加荷龄期无关的假设与实际不符。文献［4］针对指数形式的徐变度表达式，提出了无需记录应力历史的全量方法，得到了大体积混凝土结构应力徐变计算公式，大大提高了计算效率。文献［5］提到叠加法是以应变与应力成线性关系的假设作为依据，递增应力历史时叠加法徐变计算值与试验值基本相符。文献［6］基于叠加法推导出弹性后效徐变恢复表达式，提出徐变的双功能函数全量递推表达式，最终徐变计算值与叠加法计算值差异很小。文献［7］在叠加法的基础上利用积分中值定理，推导出含有老化系数的龄期调整有效模量法，计算简便，但精度依赖于老化系数的取值。文献［8］进一步研究龄期调整有效模量，得到含有2 个中值系数的计算式，可分别描述弹性应变、徐变应变对总应变的影响。文献［9］基于徐变的可逆性原理，结合中值定理，推导出不需要记录全部应力历史的全量递推表达式，较大幅度地提高了计算效率，且能够满足工程需要。许多学者对不同类型混凝土的徐变恢复进行了大量研究。文献［10］在试验的基础上，对混凝土徐变恢复影响因素进行分析，得出徐变恢复与加载龄期、应力持荷时间、卸载龄期、卸载持续时间有关，而与温度和湿度无关的结论，并基于试验建立了可行的徐变恢复预测模型。文献［11］发现混凝土徐变恢复受混凝土强度的影响。文献［12］建立了高强度混凝土的徐变恢复修正模型，并验证了其合理性。

在变化应力的徐变计算中，一类方法高估或低估徐变恢复的作用；另一类方法虽然考虑了徐变恢复作用，但较少对复杂应力历史进行分析。为解决复杂应力历史的徐变计算问题，研究徐变恢复对混凝土徐变应变、总应变的影响，本文采用双函数法对叠加法的徐变计算公式进行修正，推导适用于不同状态应力历史的徐变计算公式。

1 徐变计算理论

现有徐变计算方法和理论包括有效模量法、叠加法、弹性老化理论、徐变率法和绩效流动理论。经试验验证，叠加法计算值与试验值基本吻和，能够满足工程需要［5］。叠加法对t时刻的徐变εcr(t)可表示为

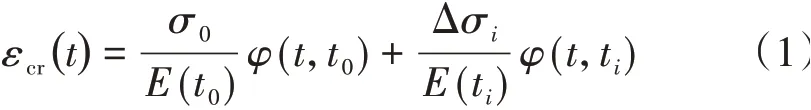
采用积分形式可表示为

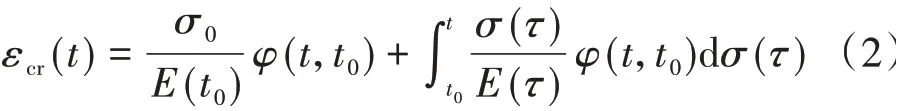
式中：σ0，E(t0)分别为初始加载龄期t0的应力、弹性模量；φ(t，t0)为徐变系数；Δσi=σi-σi-1为在ti时刻的应力增量；σ(τ)和E（τ）分别为任意时刻的应力、弹性模量。

叠加法认为卸载后的徐变恢复曲线与加载徐变曲线一致［6］，所以其徐变恢复度C(t，t0，t1)可表示为

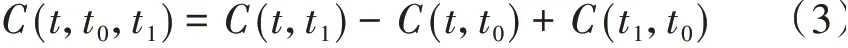
式中，C(t，t0)=φ(t，t0)∕E(t0)，为徐变度。

2 考虑徐变恢复的叠加法修正

2.1 简单应力下叠加法修正

由于叠加法计算递减应力时高估了混凝土徐变恢复，文献［13］在叠加法的基础上提出了简单应力历史（图1）的双函数计算公式，见式（4）。

图1 简单应力历史示意

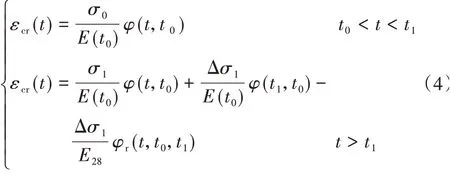
式中：φr(t，t0，t1)为徐变恢复系数；E28为混凝土28 d 弹性模量。

由式（4）可知，t时刻的徐变可视为图1 中上下2块矩形应力历史对t时刻徐变作用的叠加。下方矩形、上方矩形（阴影）应力历史对时刻t的徐变分别为对于下方矩形应力历史，可理解为加载时刻t0应力作用下对时刻t的徐变为卸载时刻t应力作用下对时刻t的徐变为同理，图1 上方矩形（阴影）应力历史也可理解为加载时刻t0与卸载时刻t1的应力作用下对时刻t的徐变，分别为

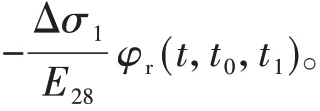
2.2 阶梯变化应力下叠加法修正

基于式（4）的应力分割原理，可把复杂的阶梯变化应力历史分割为多个矩形应力，然后在把多个矩形应力历史对时刻t的徐变进行线性叠加，最终求出时刻t的徐变。对于阶梯变化应力历史，可分为几个简单矩形应力历史，见图2。

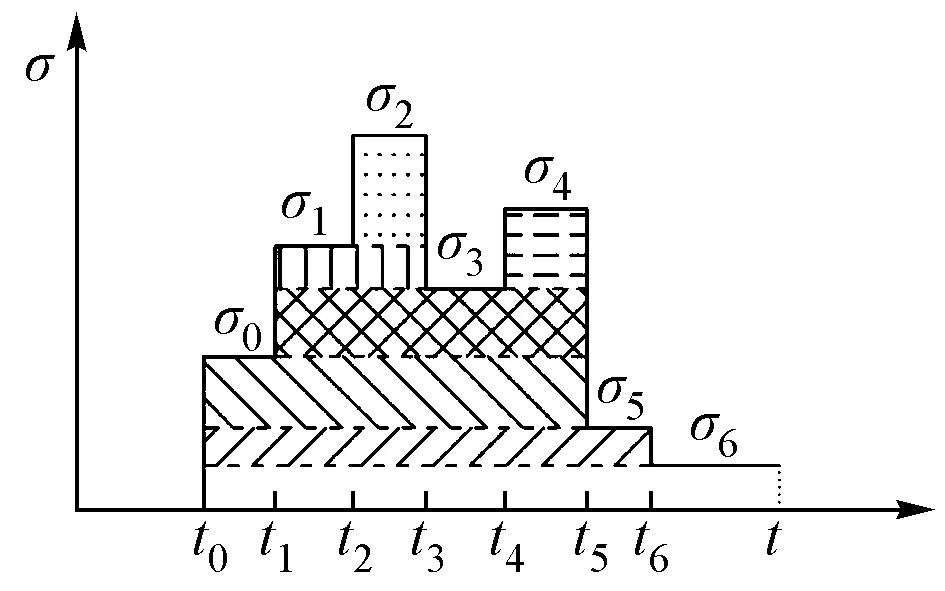
图2 阶梯变化应力历史

分别计算每一个加卸载简单应力历史的徐变再叠加，则时刻t的徐变可表达为

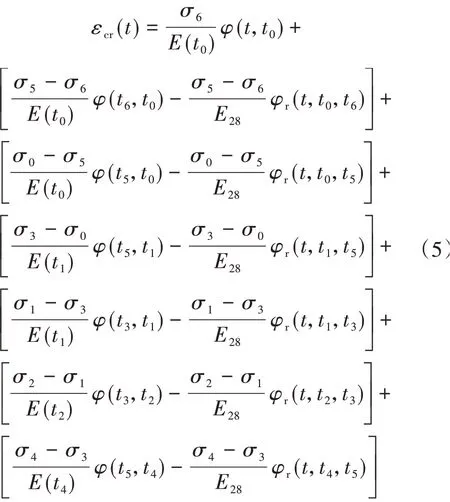
对于应力局部减小且减小幅值较大时，需要确定递减应力下不同的加载时刻。图2 中对于t5的卸载时刻，卸载应力幅值为|Δσ5|=σ4-σ5，其变化较大，可分为多个应力加载σ0-σ5，σ3-σ0，σ4-σ3，加载时刻分别为t0，t1，t4。

综上所述，对于阶梯变化应力历史的混凝土徐变计算可表达为

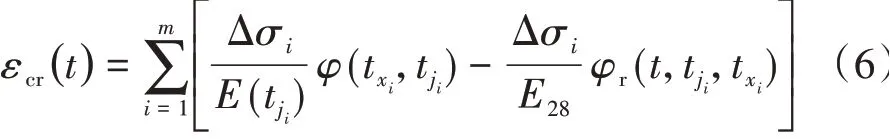
式中：m为从初始加载龄期t0到计算时刻t离散为矩形应力历史的个数；tji，txi分别为第j个简单加卸载应力历史的加载、卸载龄期。

2.3 连续变化应力下叠加法修正

类似于阶梯变化应力历史的应力分割原理，可推导连续变化应力历史（图3）的徐变计算式。当计算时刻t的徐变应变时，可分为如下5种情况。

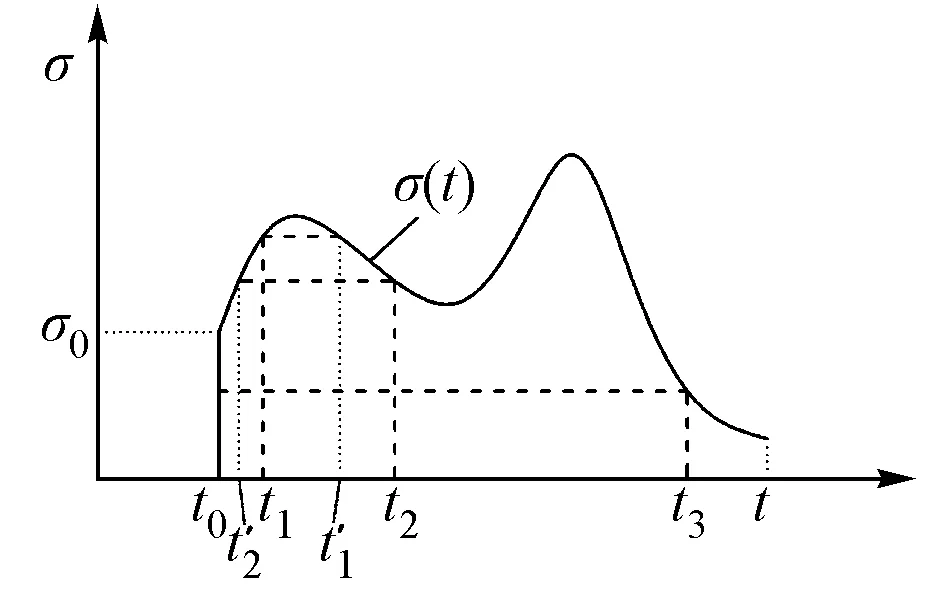
图3 连续变化应力历史示意

1）τ∈[t0，t]，σ'(τ) > 0，且不存在τm∈[τ，t]，使得σ（τm）=σ（τ），则时刻τ应力增量对时刻t产生的徐变可表示为

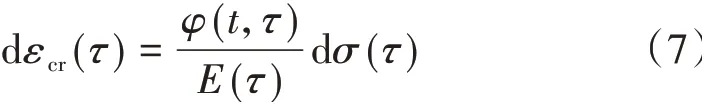
2）τ∈[t0，t]，σ'(τ) > 0，且存在τm∈[τ，t]，使得σ（τm）=σ（τ），则时刻τ应力增量对时刻t产生的徐变可表示为

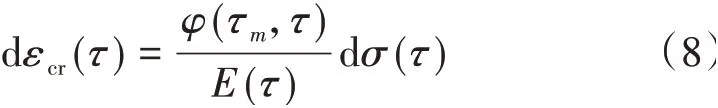
其 中，τm= min(τm1，…，τmx)，τm1，…，τmx均 满 足σ(τmi) =σ(τ)。

如图3 所示，当τ=t1时，存在τm=t'1使得σ(t1)=σ(t'1)，则时刻t1的应力增量对时刻t徐变可写dεcr(t1)=

3）τ∈[t0，t]，σ'(τ) < 0，且不存在τn∈[t0，τ]，使得σ(τn) =σ(τ)，则时刻τ应力增量对时刻t产生的徐变可表示为

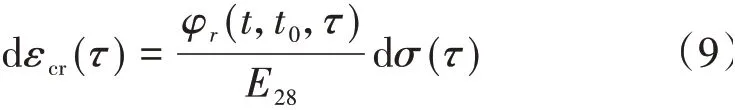
如图3 所示，不存在τn，所以时刻t3的应力增量对时刻t的徐变可写为

4）τ∈[t0，t]，σ'(τ) < 0，且存在τn∈[t0，τ]，使得σ(τn) =σ(τ)，则时刻τ应力增量对时刻t产生的徐变可表示为

其 中，τn= max(τn1，…，τny)，τn1，…，τny均 满 足σ(τni) =σ(τ)。

如图3 所示，当τ=t2时，存在τn=t'2，使得σ(t'2)=σ(t2)，所以时刻t2的应力增量对时刻t的徐变可写为

5）上述4 种情况是计算变化应力对时刻t的徐变，τ∈[t0，t]范围内最小应力min[σ(τ)]对时刻t的徐变可用式（11）计算。对于图3 应力历史，

min[σ(τ)]=σ(t)。

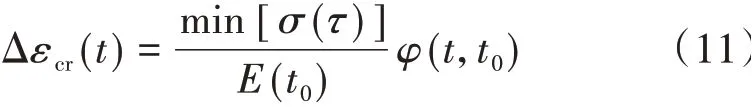
综上所述，计算时刻t的徐变应变可表达为

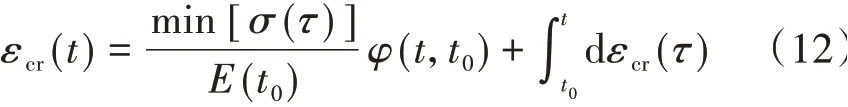
为表达方便，令dεcr(τ) =f(τ)dσ(τ)，则有

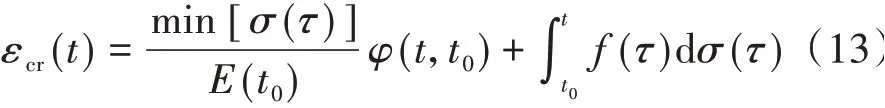
3 计算模型的选取

3.1 徐变模型的对比与选取

由于影响徐变的因素较多，国内外许多学者对徐变做了大量研究，得到了适合本国的模型。本文主要将ACI 209R⁃92 模型［14］、GL2000 模型［15］、CEB⁃FIP1978模型［16］以及JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》［17］（以下简称18桥规）中模型进行对比，分析其中的差异。

从徐变影响因素方面，4 种模型均考虑了加载龄期、计算龄期、构件截面尺寸、环境相对湿度，但考虑方法及影响程度却各不相同。其他相对次要的因素，各模型考虑并不一致，如ACI 209R⁃92 模型对混凝土内部构成及前期工艺方法（空气含量、细骨料比重、坍落度、养护方法）考虑比较全面。

从徐变的发展形式来看，4 种模型表达方式不一致：ACI 209R⁃92 模型采用双曲函数表达徐变系数；GL2000 模型则采用分段函数；CEB⁃FIP1978 模型将徐变分成可恢复徐变、不可恢复徐变、初始不可恢复变形3 个部分；18 桥规模型则采用整体函数描述徐变规律。

18桥规在我国应用较为广泛，所以本文选取18桥规模型作为徐变系数计算模型。其公式为

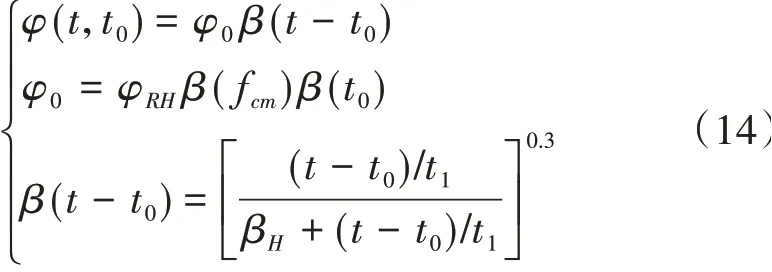
式中：φ0为名义徐变系数；φRH，β(fcm)，β(t0)分别为湿度RH、混凝土强度fcm、加载龄期t0对名义徐变系数的影响系数；β(t-t0)为徐变发展函数；βH为湿度对徐变发展函数的影响系数。

3.2 徐变恢复模型的对比与选取

不同学者提出了一系列的徐变恢复模型，包括文献［13］中提到的CFB⁃FIP1978模型（MC78模型）、改进CEB⁃FIP78 模型（IMC78 模型）、修正求和模型（RSM 模型），以及文献［18］中的双曲幂模型。MC78 模型及IMC78 模型认为徐变恢复系数终值为常数，但是考虑徐变恢复发展方式不同。MC78 模型采用双曲函数描述徐变规律，IMC78模型采用指数形式。双曲幂模型、RSM 模型则考虑加载龄期、应力持时、强度对徐变恢复的影响，与试验结果吻合较好，但是RSM 模型输入参数较多，计算复杂。双曲幂模型考虑因素较为全面，与试验值吻合度较高，计算简便。因此，本文选取双曲幂模型作为徐变恢复计算模型。其公式为

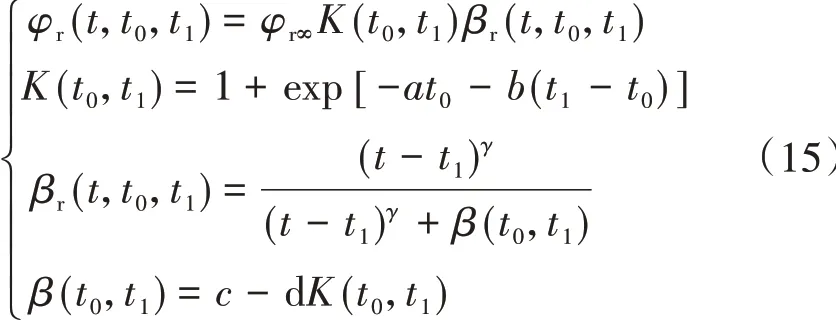
式 中：φr∞为 徐 变恢 复系 数终 值，取0.35；K(t0，t1)，β(t0，t1)分别为加载龄期、荷载持时对徐变恢复系数终值、徐变发展函数的影响系数；βr(t，t0，t1)为徐变恢复发展函数；a=0.12，b=0.005 5，c=7，d=3，γ= 0.5。

4 实例应用与对比分析

4.1 概况

为分析叠加法与修正叠加法的差异，本文设计混凝土强度等级为C50，所处的环境湿度为60%，温度为20℃，构件截面尺寸为120 mm×120 mm，构件采用全截面受压，E28= 35.5 GPa，混凝土弹性模量随时间的变化参考CEB⁃FIP1978模型［16］，其公式为

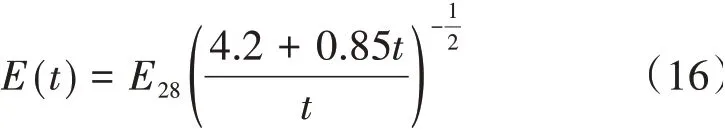
设置3 组阶梯变化和2 组连续变化应力历史。3组阶梯变化应力历史分别为阶梯递增、阶梯递减与阶梯波动应力历史，其初始加载时刻均为100 d，其后每100 d变化1次应力，累计变化6次，最终徐变计算时刻为700 d。2 组连续变化应力历史的初始加载时刻为100 d，徐变计算终止时刻为700 d。连续波动变化应力历史函数为

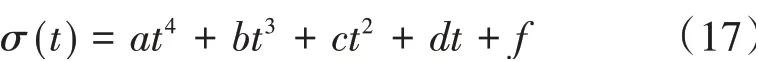
式 中：a= -1∕240 000 000，b= 67 ∕10 000 000，c=-2 219 ∕600 000，d= 803∕1000，f= -228∕5。

连续递减应力历史函数为

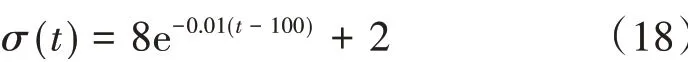
阶梯变化应力和连续变化应力历史见图4。

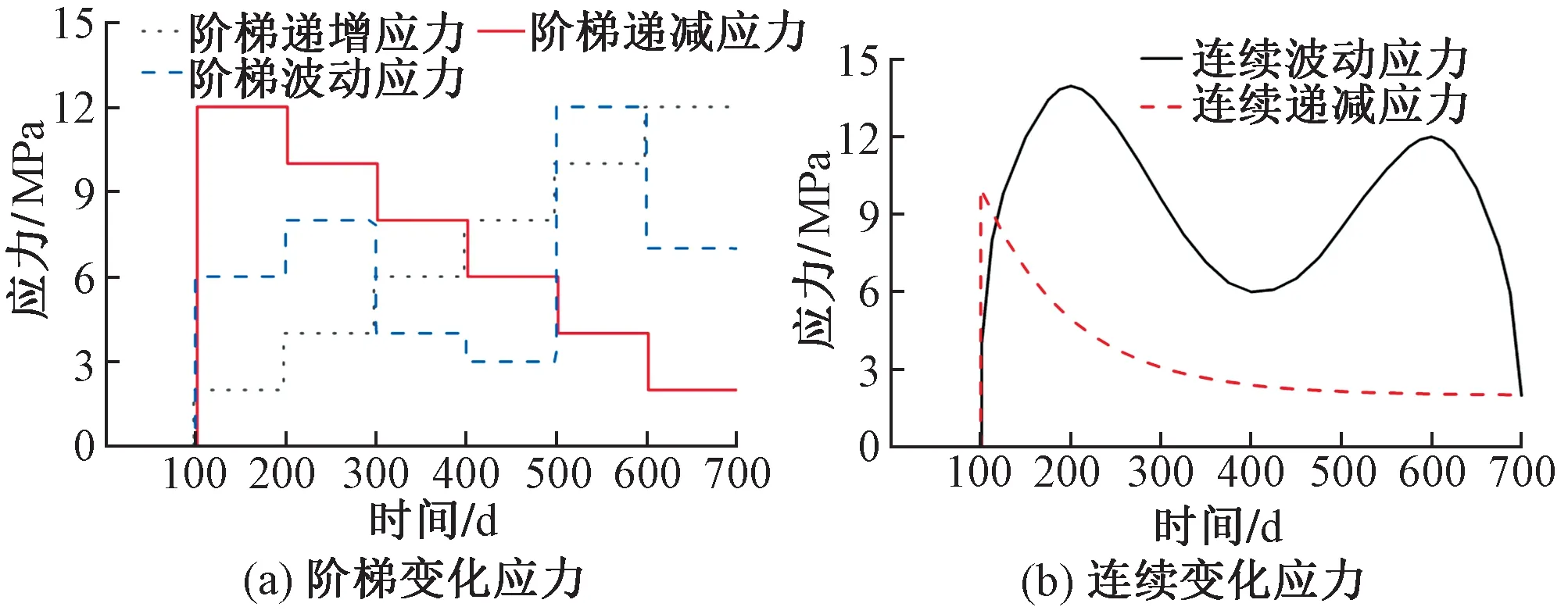
图4 应力历史

4.2 徐变计算与对比分析

本文采用MATLAB计算阶梯变化应力历史下2种方法的徐变应变、总应变（弹性应变+徐变应变），见图5。

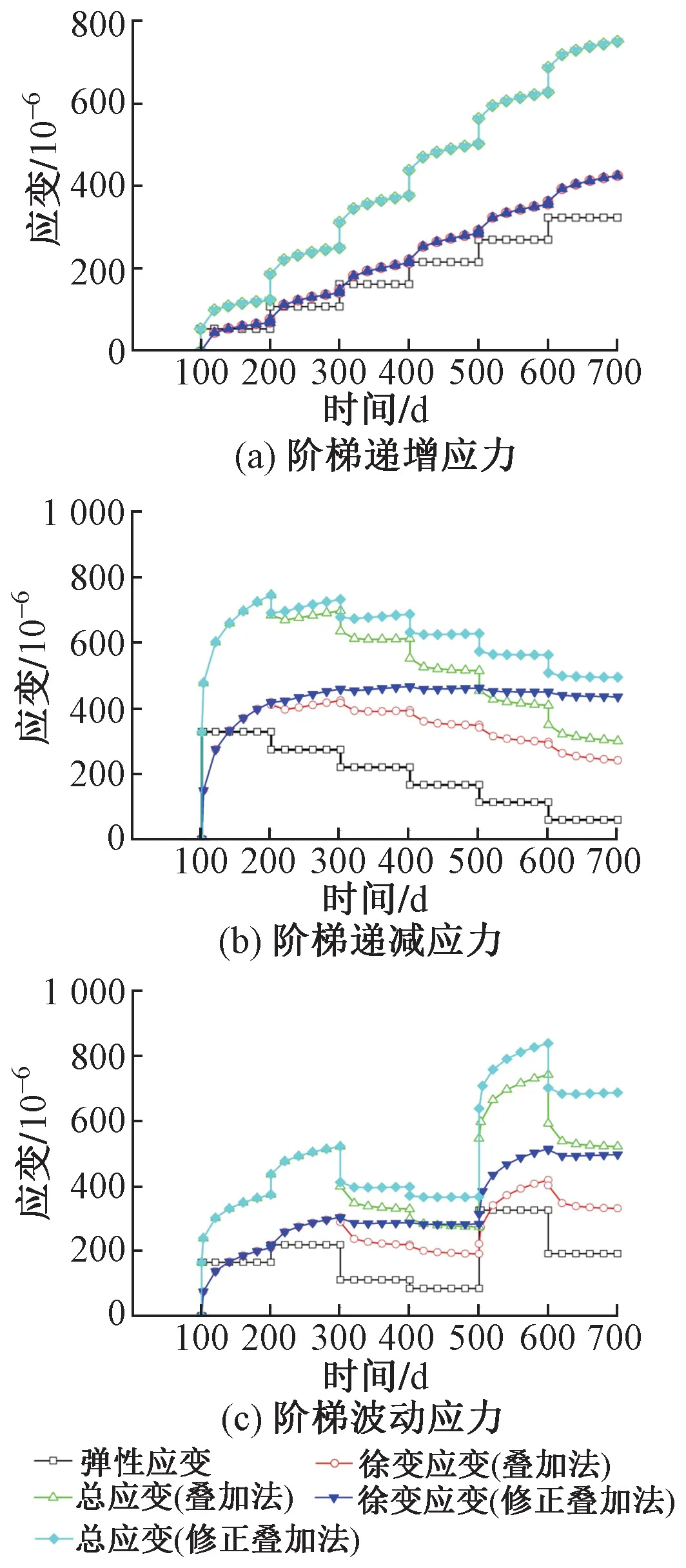
图5 阶梯变化应力下的徐变应变、总应变

由图5（a）可知，叠加法和修正叠加法在递增应力历史下计算的徐变应变、总应变一致。由图5（b）和图5（c）可知，弹性应变和受力状态变化一致；在应力初始加载及递增应力作用下，2 种方法计算的徐变应变、总应变一致。在应力首次卸载后，修正叠加法计算的徐变应变、总应变比叠加法要大。原因是修正叠加法考虑的徐变恢复系数比叠加法小，叠加法低估了混凝土徐变效应。应力减小量越大、持续时间越长，2种方法的徐变应变差异越大。对于阶梯递减、阶梯波动应力历史，700 d叠加法计算的徐变应变比修正叠加法分别小44%，33%，总应变分别小39%，24%。

连续变化应力历史下2 种方法计算的徐变应变、总应变见图6。

由图6（a）可知：①100 ～200 d 时，由于应力是连续增加的，叠加法和修正叠加法计算的徐变应变和总应变一致；②200 ～400 d 时，2 种方法的徐变应变和总应变差异逐渐增大；③400 ～600 d 时，应力递增不会引起2 种方法徐变应变差异，同时由于前期应力递减引起的徐变恢复基本完成，因此2 种方法的徐变应变曲线基本平行。对于连续波动应力历史，700 d叠加法计算的徐变应变、总应变比修正叠加法分别小42%，

38%。

由图6（b）可知：①在初始龄期加载后，总应变短暂上升，后面一直呈递减趋势；②2种方法计算的徐变应变、总应变在应力加载后便有差异，且随着时间的增加差异进一步增大；③叠加法计算的徐变应变先增加，再逐渐减小后趋于稳定；修正叠加法计算的徐变应变先增加后趋于稳定。对于连续递减应力历史，在700 d 徐变计算时刻，叠加法计算的徐变应变、总应变比修正叠加法分别小47%，39%。

综上所述，修正叠加法在计算复杂应力的徐变时与叠加法存在一定的差异。在应力减小的情况下，修正叠加法准确考虑了混凝土徐变恢复，其计算值更接近实际值。

5 结论

1）对于递增应力历史，叠加法与修正叠加法计算的徐变是一致的。对于递减应力历史，2 种方法计算徐变应变的差异随时间逐渐增大，700 d徐变相对误差最大为47%。

2）不同的应力历史2种方法徐变计算值的差异不同。递减应力历史差异最大，波动应力历史次之，递增应力历史无差异。

3）修正叠加法考虑了真实混凝土徐变恢复，适用于不同徐变模型、不同应力历史，为实际工程提供了一种精确的徐变计算方法。