非均匀正交各向异性端头帽热应力分析①

程兴华，李建林，杨 涛，李 理

(国防科技大学航天与材料工程学院，长沙 410073)

0 引言

高超声速飞行器在出入大气层或持续在大气内飞行时，将承受巨大的气动力和气动热。气动热载荷表现为表面与大气的摩擦而达到较高的温度，尤其是飞行器头锥、翼前缘等部位。气动热不仅使材料的力学性能降低，而且在结构中产生热应力，从而使变形加剧，高温热载荷引起的热应力不容忽视。以往对高温区的温度、热应力分析多为非线性、正交各向异性，而对复合材料因编织方法引起的物性非均匀性分析很少[1－5]。

本文以正交各向异性复合材料端头帽为对象，研究非均匀材料物性引起的应力分布变化。

1 计算模型

1.1 热弹性本构方程

在弹性力学中，应力和应变关系由广义胡克定律确定。胡克定律是固体弹性材料在均匀常值温度下的本构方程，如考虑温度变化的影响，而不考虑温度与变形之间的耦合关系，则材料的本构方程[6]可记为

式中cijkl为弹性模量，也称刚度系数;εkl为应变张量;βij是在应变为零时测得的热模量，是一个对称张量;T为当前温度;T0为参考温度，即cijkl测定时的温度。

式(1)中的温度变化ΔT一般用符号Θ来表示，这样式(1)即可写作:

式(2)称为杜哈梅尔-牛曼(Duhamel-Neumann)关系式。

1.2 瞬态传热本构方程

热弹性理论离不开对传热规律的了解，传热有传导、辐射和对流3种形式。其基本的能量守恒方程为

式中V为固体材料的体积;S为表面积;ρ为材料密度;U·为内能的时间变化速率;q为单位表面积上流入控制体的热流率;r为单位体积内的其他热增量。

假设U=U(T)，T为材料的温度，q和r与材料的应力和位移无关。除相变产生的潜热外，传热分析的本构方程为

其中，c(T)为材料的比热容，当给定潜热时，认为它是比热容的一个附加量。多数情况下，认为相变在一定的温度范围内发生是合理的。

导热遵守傅里叶定律:

式中 λi为热导率。

物体中的温度分布，无论是定常还是非定常，都需要给定边界条件[7－8]，对于非定常情况还须给出时间的初始条件，这才能求解方程(3)内的温度分布。

2 数值方法

2.1 顺序耦合算法

持续受热的特征决定了飞行器在某一时刻的受热情况不仅与这一时刻的飞行条件有关，还与这之前飞行器自身热环境所经历的时间历程紧密相关。在以往气动加热分析中，多数研究的是瞬态情况，即在一定的飞行(来流)条件和外表面壁温条件下给出外表面的热流分布。这种瞬态结果尚不足以用来判断飞行器在持续受热过程中的各种中间状态，因为在各个中间状态对应的物体自身热环境都是经历了一定时间历程后形成的，考虑各传热环节之间的耦合性十分必要。

顺序耦合算法又称松耦合方法，其特点是流场与结构计算域在接触面上周期性交换数据，主要体现为流体与结构接触面上的边界条件处理。

本文通过Fortran用户子程序对大型非线性有限元计算软件Abaqus进行二次开发。每个时间增量步开始时，用户子程序读取端头帽外表面上的温度，将计算得到的气动热流传递给Abaqus主程序;Abaqus主程序根据边界热流进行热应力计算;如此顺序耦合循环，直至弹道结束点，最终完成端头帽热应力分析。

2.2 物理数学模型

端头帽为球锥结构，如图1所示，球头半径为RN，锥身半锥角θ，总长L。由对称性，考虑计算工况含有攻角、材料的正交各向异性，数学模型取周向180°。xy平面为端头帽对称面，α为攻角，αg为子午面与xy平面的夹角。

网格划分如图2所示。由于头部热流梯度比较大，对头部网格进行了适当加密。网格单元选取耦合温度——位移单元C3D8T和C3D6T。

图1 模型三维视图Fig.1 3D view of them odel

图2 网格划分Fig.2 M esh for discretization

2.3 材料模型

端头帽材料以周向0°、90°正交编织，材料沿端头帽轴向性能一致。由于x、z方向(与端头帽轴线垂直的平面)交错叠加，消除了x、z方向性能差别，但不能消除xz平面内45°方向的性能差异，即材料性能在xz平面内呈现非均匀性。根据测试结果，在45°方向主要是力学性能(弹性模量E)的差异，热物理性能(表1)差异很小，在本文研究中可忽略。

根据以往双向拉伸性能试验，可判断在与炭布x向或z向的夹角为45°时，材料的模量和强度减小到x向或z向的70%。

端头帽材料模型如图3所示。材料力学性能在xz平面内绕y轴以90°周期分布。在第Ⅰ象限内，以材料在x方向的力学性能为标准(100%);当0°＜αg＜45°时，材料力学性能随αg增大而减小;至αg=45°时，力学性能减小至x方向的70%;当45°＜αg＜90°时，材料力学性能随αg增大而增大;至αg=90°时，力学性能增大至100%，与x方向性能一致。本文采用线性插值方法获取αg在不同角度时的端头帽力学性能。端头帽在主轴方向的力学性能如表2所示。

2.4 初边值条件

端头帽弹道曲线如图4所示。设端头帽初始温度均匀分布，取300 K，计算总时间为977 s。

表1 端头帽材料热物理性能Table 1 Thermal physical properties of the nosecap material

图3 力学性能插值示意图Fig.3 Interpolation sketch for mechanics properties

表2 端头帽材料力学性能Table 2 M echanics properties of the nosecap material

图4 端头帽弹道曲线Fig.4 Flight trajectory of the nosecap

弹头在大气环境下高速飞行，不仅受气动力作用，还受气动加热作用。端头帽的边界条件有热边界、气动压力边界、对称边界、连接支撑边界。

(1)热边界为端头帽外表面，受气动加热作用，同时向外部环境空间辐射热量。

本文采用Lees模型[9]计算气动加热热流通量:

式中Q为进入表面的热量;S为边界表面;t为时间;ψ(x，y，z，t)为给定的热流通量函数。

端头帽为热结构，表面辐射到环境空间的热力密度为

式中 εr为端头帽表面热辐射率，一般假设εr=0.8;σr为波尔兹曼常数，σr=5.67×10－8;Tb为端头帽的表面温度;Tair为环境大气温度。

(2)气动压力边界同样作用在端头帽的外表面，压力值由已知条件给出。

(3)对称边界为端头帽纵对称面，在对称面上:

式中U3为z方向的位移;UR1为绕x轴的旋转;UR2为绕y轴的旋转。

(4)连接支撑边界为端头帽尾部，与弹体连接，假设连接支撑边界为固支。

3 结果分析

3.1 温度分布

表面节点温度变化主要受气动加热和热辐射影响，当气动加热与热辐射平衡时，节点温度达到极大值。图5为0°攻角母线温度变化曲线，可见驻点附近温差较小，驻点最高温度为2 356 K;在弹道前段，表面温度在球头沿母线急剧下降，而在锥身下降缓慢;在弹道末段，由于高温的强辐射作用，端头帽球头温度较锥身下降快;977 s时球头温度低于锥身温度，端头帽最低温度在驻点(约1 001 K)，最高温度在尾部轴线上(约1 049 K)。由此可见，在弹道末段，端头帽内部温度较高，表面热辐射大于气动加热，端头帽向外放热。

图6为0°攻角典型时刻的温度云图。由于热导率较小，在870 s以前，高温区主要集中在端头帽球头，温度梯度较大，而在锥身部温度分布较为均匀、梯度较小。在870 s后，高温区向锥身扩展，但此时最高温度已小于1 200 K，最大温差小于50 K，整体分布较均匀，温度梯度较小。另外，由于辐射换热与表面温度的四次方成正比，在260 s以前，辐射换热小于气动加热，驻点温度急剧升高;之后，辐射换热大于气动加热，驻点温度逐渐减小，驻点位置由向内加热转为向外放热。

图5 0°攻角母线温度变化Fig.5 Temperature profile along generating line under 0°angle of attack

图6 0°攻角温度云图Fig.6 Temperature distributions under 0°angle of attack

3.2 应变-应力分布

在复合材料的强度准则中以最大应变准则和最大应力准则、蔡-希尔准则、蔡-吴准则[10]应用的较多。Mises等效应力可以看作蔡-吴准则的一个特例，其定义为

其中，S为偏应力张量，S=σ+p I(σ为应力，I为单位矩阵，p=－σii/3为等效压应力，也就是常见的p=(σx+σy+σz)/3)。因此，以下重点对端头帽的应变和Mises等效应力进行分析。

图7为0°攻角典型时刻主弹性应变云图，图8为0°攻角典型时刻x向热应变云图。由图7、图8可知，弹道初段，由于端头帽头部高温区集中，局部大热膨胀拉伸头部，使得头部出现环形大弹性应变区域;弹性应变较热应变为小量，总应变分布与热应变分布相同，大小基本相当。在弹道中段、末段，高温区向后移动，端头帽尾部固定端的弹性应变凸显出来，总应变在端头帽尾部以约束条件产生的弹性应变为主，而其余主体部分仍以热应力为主。

图7 0°攻角主弹性应变云图Fig.7 Principal strains distributions under 0°angle of attack

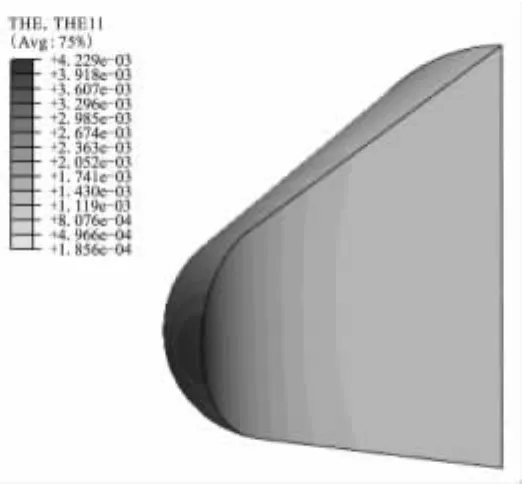
图8 0°攻角x向热应变云图(t=120 s)Fig.8 x direction thermal strain distributions under 0°angle of attack(t=120 s)

图9为0°攻角典型时刻Mises应力云图。由图9可知，在弹道初段，由于热膨胀作用，端头帽外表面形成环状Mises应力分布，内部也存在较大应力;在弹道末段，热应力较小，尾部由于固定约束而形成较大的应力。在热应力集中段，外表面Mises应力最大;在尾部约束处，内部Mises应力最大。在垂直于y轴的剖面上，Mises应力分布以90°为周期(如图9中的尾端面应力云图)，在0°、90°方向最大，逐渐过渡到最小的45°方向。

3.3 攻角对温度、应力的影响

受攻角影响，头部驻点下移(最大温度2 351 K)，低温点上移，在尾部背风位置附近。高温区域仍集中在头部，由于头部为球形，其以驻点为中心的分布趋势与0°攻角时基本相同。图10为10°攻角母线温度分布曲线。由图10可知，10°攻角时，迎风母线(αg=180°)温度最高，侧面水平母线(αg=90°)近似为迎风和背风母线(αg=0°)的平均值。

图9 0°攻角M ises应力云图Fig.9 M ises equivalent stress distributions under 0°angle of attack

图10 10°攻角母线温度分布(t=260 s)Fig.10 Tem perature profile along generating line under 10°angle of attack(t=260 s)

图11为10°攻角x向热应变云图。由图11可见，除约束端外，10°攻角端头帽总应变在弹道初段仍以热应变为主。热应变集中在球头部，以攻角α=10°的球头径向对称分布;总应变最大值在驻点附近;主弹性应变在迎风面较大，高弹性应变区域在迎风面较宽。

对应于应变分布，弹道初段Mises应力在迎风面上出现极大值，且呈现较宽区域的应力集中(图12)。弹道末段，10°攻角Mises应力轴向分布与无攻角时基本相同:热应力较小，尾部由于固定约束而形成较大的应力。受攻角和材料性能参数的双重影响，在垂直于y轴的剖面上，Mises应力在αg=180°子午面内最大，αg=45°子午面内最小(图13)，这种现象在弹道初段最为明显。分析可知，最大Mises应力为111 MPa，较无攻角时(104 MPa)略大。

图11 10°攻角x向热应变云图(t=260 s)Fig.11 x direction thermal strains distributions under 10°angle of attack(t=260 s)

图12 10°攻角M ises应力云图(t=110 s)Fig.12 M ises equivalent stress distributions under 10°angle of attack(t=110 s)

图13 10°攻角尾部外表面周向M ises应力分布Fig.13 Circum ferential M ises stress distributions on tail surface under 10°angle of attack

在端头帽结构设计时，应将材料的xz平面45°方向设置在迎风线上。这样可减小端头帽应力极值，使端头帽周向应力分布趋于均匀，有利于端头帽与弹体连接。

4 结论

(1)弹道初段，表面热辐射小于气动加热，端头帽温度迅速升高;弹道末段，端头帽内部温度较高，表面热辐射大于气动加热，端头帽向外放热。有攻角时，侧面水平母线温度近似为迎风和背风母线平均值。

(2)弹道初段，局部大热膨胀拉伸头部，在头部形成环状弹性应变区。在弹道中、末段，高温区向后移动，总应变在端头帽尾部以固定约束条件产生的弹性应变为主，而其余主体部分仍以热应力为主。因此，端头帽尾端的连接方式十分重要。

(3)在垂直于端头帽y轴的剖面上，Mises应力分布以90°为周期，在0°、90°方向最大，逐渐过渡到较小的45°方向。

(4)受攻角影响，Mises应力在迎风子午面内最大，水平子午面内最小，这种现象在弹道初段最为明显。在端头帽结构设计时，应将材料的xz平面45°方向设置在迎风线上。

[1] Grant Palmer.A heating analysis of the nosecap and leading edges of the X-34 vehicle[R].AIAA 98-0878.

[2] 尹莲花，刘莉，张帅.烧蚀材料的近程高速弹头热应力数值仿真研究[J].系统仿真学报，2008，20(15):3966-3968.

[3] 姜志杰，张擘毅，何浩.高超声速飞行器鼻锥的热环境和结构热分析研究[J].导弹与航天运载技术，2009，(4):14-17.

[4] 易龙，孙秦，彭云.复合材料头锥结构气动热应力分析方法研究[J].机械强度，2007，29(4):686-692.

[5] Rosario Borrellia，Aniello Riccio，Domenico Tescione.Thermo-structural behaviour of an UHTCmade nosecap of a reentry vehicle[J].Acta Astronautica，2009，65:442-456.

[6] 范绪箕.高速飞行器热结构分析与应用[M].北京:国防工业出版社，2009.

[7] 朱滨.弹性力学[M].合肥:中国科学技术大学出版社，2008.

[8] 赵镇南.传热学[M].北京:高等教育出版社，2002.

[9] 中国人民解放军总装备部军事训练教材编辑工作委员会.高超声速气动热和热防护[M].北京:国防工业出版社，2003.

[10] 王宝来，吴世平，梁军.复合材料失效及其强度理论[J].失效分析与预防，2006，1(2):13-19.