高阶控制导弹线性二次型微分对策制导律①

花文华，陈兴林

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

近年来，微分对策理论在飞行器姿态控制[1]、威胁规避[2]、火力分配[3]，目标拦截[4]等方面得到了较为广泛的研究。在目标拦截中，由于目标的独立性，其机动策略一般是无法预测的。因此，将拦截情形定义为最优控制问题并不合适[5]，而对于微分对策双边优化问题而言，双方都是独立控制的，一方要求性能指标的最大化，而另一方要求性能指标的最小化。

文献[6]假设目标是静止的，给出了一种具有终端碰撞角度约束且适用于任意阶控制导弹的最优制导律。文献[7]考虑任意阶导弹机动动态，给出了一种满足终端角度约束的微分对策制导律，但在具体推导过程中，为得到解析解，假设拦截导弹和目标具有理想机动动态，使得最终结果并不适用于任意阶控制的拦截导弹和目标的情形。本文基于微分对策双边优化理论，给出了一种可适用于具有任意阶控制的拦截导弹和目标的一般形式微分对策制导律。首先，对所要研究的问题进行描述和建模，给出任意阶控制的拦截导弹和目标的状态方程;然后，进行一般形式微分对策制导律的推导，给出解析解;针对一类具有一阶正当传递函数的拦截导弹，进行制导律的验证和仿真，给出该情形下的制导增益和对策空间分析。

1 问题描述及建模

制导末端的弹目运动关系如图1所示，X轴沿初始视线方向，下标P和E分别对应拦截导弹和目标的相关状态，y表示拦截导弹和目标相对于初始视线方向的位移。基于下述假设进行问题分析:

(1)拦截导弹和目标可近似为具有线性动态特性的质点，并可沿初始视线方向进行线性化;

(2)拦截导弹和目标速度大小不变，导弹机动能力大于目标。

图1 平面弹目运动关系Fig.1 Planar engagement geometry

基于图1和假设(1)，拦截导弹和目标相对运动关系可表示为

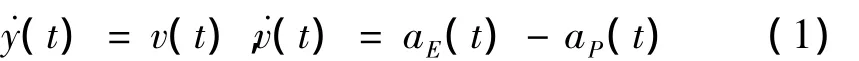
n阶导弹机动动态为

式中aP为导弹加速度;pP为其余的(n－1)个状态变量;a1和b1为标量;a21，aT12和b2为(n－1)×1的向量;a22为(n－1)×(n－1)的矩阵。

参考n阶导弹机动动态定义，m阶目标机动动态可表示为

则系统状态方程可表示为

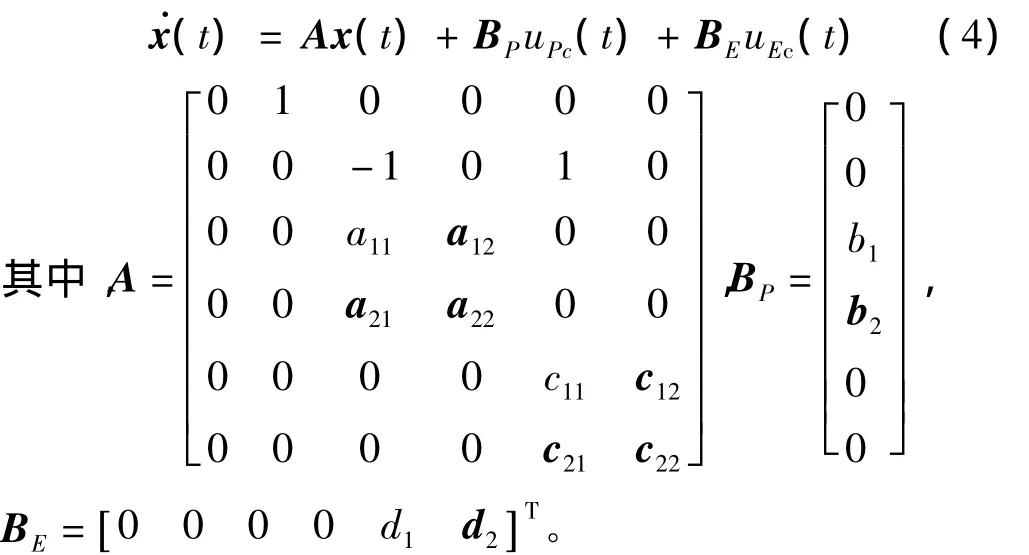
基于假设(1)和(2)，拦截导弹飞行时间为

式中r0为弹目初始距离;vc为接近速度，约为vP+vE。

待飞时间可表示为

2 微分对策制导律推导

定义线性二次型性能指标

其中，G，R，Q为加权设计参数，R＞0，Q＞0，G=diag(g00 0 0 0 0)，g0→∞表示零脱靶量拦截情形，脱靶量趋于零，g0＜∞时脱靶量为非零的有限值;Q反映了目标相对于导弹的机动能力，当假设目标具有较强的机动能力时，Q取较小值，Q→∞则表示对非机动目标拦截的情形，由假设(2)，Q/R＞1。

结合式(7)，构造哈密顿(Hamiltonian)函数:

式中 p为待定的协态向量。

由协态方程可得

其中，Φ为相应于系统状态式(4)的转移矩阵，结合横截条件，则有

由上述条件，可得拦截导弹和目标的最优控制为

将式(12)和式(13)代入式(4)，并从t～tf进行积分，可得

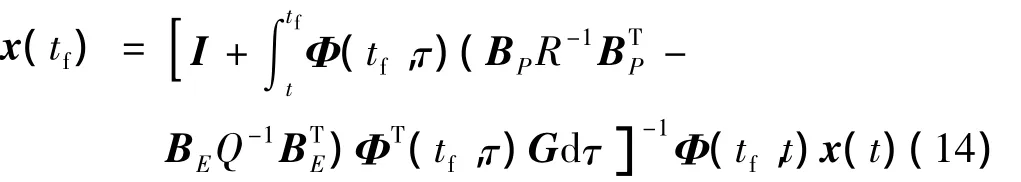
定义 D=[1 0 0 0 0 0]，结合式(4)并应用拉氏反变换，可得

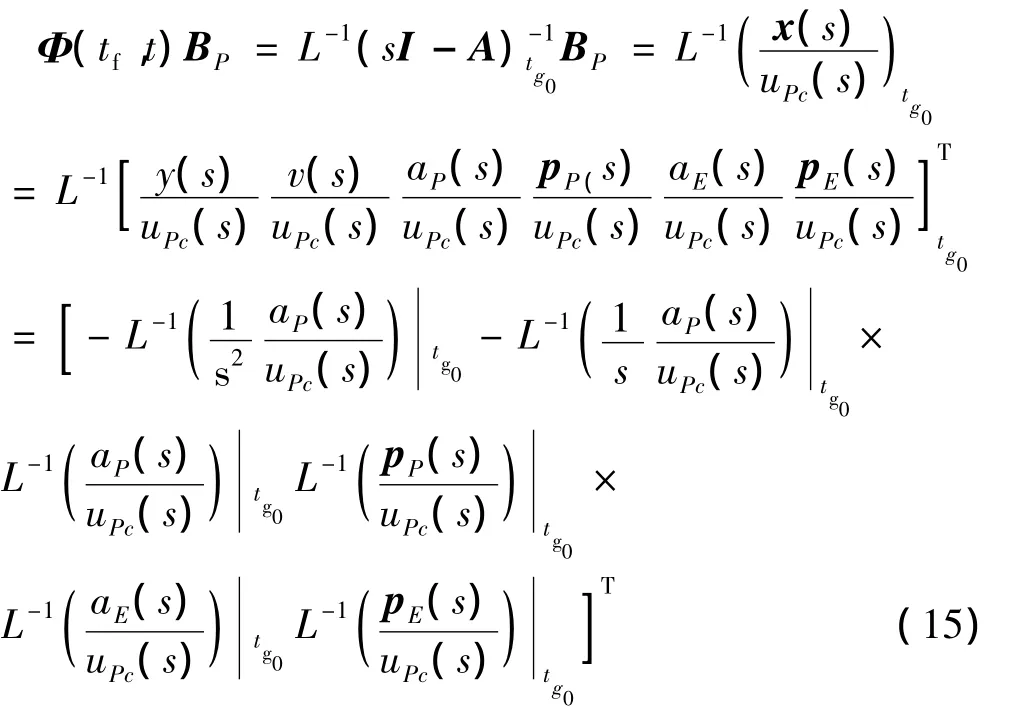
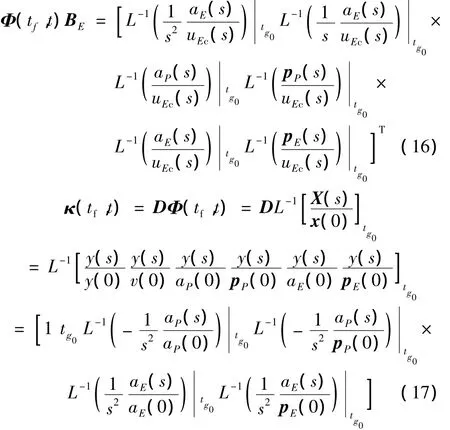
代入式(14)，可得

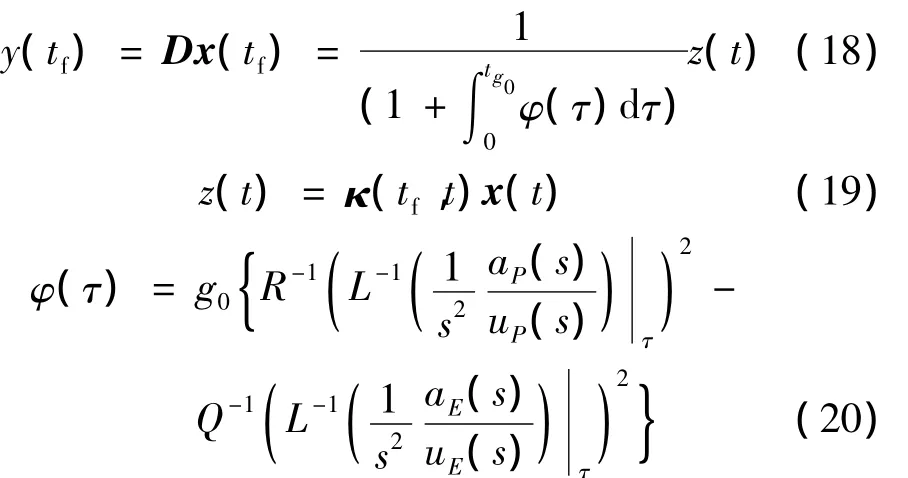
对于这一双边优化问题，z(t)表示零效脱靶量，对应于拦截导弹和目标由给定的时间t起不施加任何控制，以该瞬时参数飞行，至命中所产生的脱靶量。

将式(18)代入式(12)和式(13)，则一般形式最优制导策略可表示为

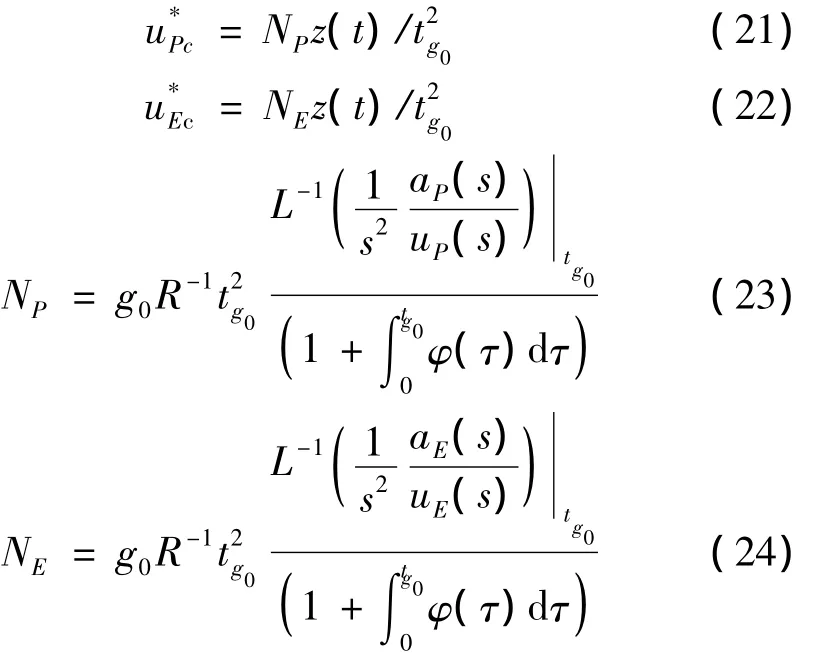
式中NP和NE分别为拦截导弹和目标制导增益。

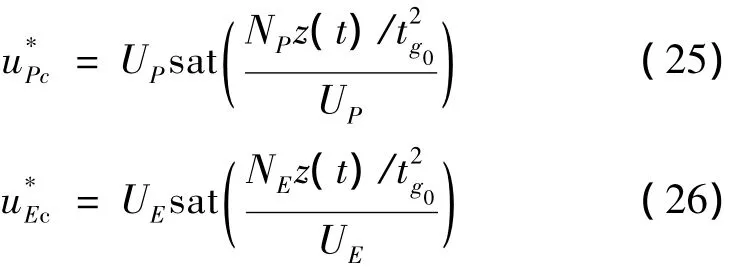
式中 sat()为饱和函数。

3 算例

3.1 制导律推导

拦截导弹机动动态采用分子分母同为一阶(biproper)的传递函数表示:

数字出版产业目前仍然存在着一些问题，例如，数字出版物的模式单一、盈利相对较少，品牌建设力量不足，数字出版物的侵权问题等。

式中d表示直接控制部分，d＞0时系统是最小相位，d＜0时系统是非最小相位;τP为导弹机动时间常数。

假设目标具有一阶机动动态特性:

式中 τE为目标机动时间常数。

为便于分析问题，定义如下无量纲变量:

目标与拦截导弹机动时间常数比:

tg0对τP的归一化:

基于高阶控制导弹和目标一般形式最优制导策略式(21)和式(22)，该类型拦截导弹和目标的最优制导策略可表示为

3.2 制导增益分析

当tg0→0时:

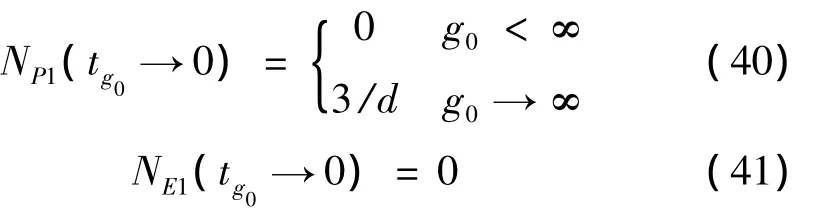
对于零脱靶量拦截情形，g0→∞，NP1与拦截导弹自动驾驶仪直接控制部分成反比。由于目标具有一阶机动动态，目标制导增益NE1趋于零。拦截导弹和目标对应于不同g0值的制导增益变化曲线如图2所示。

图2 制导增益 NP1、NE1(d=0.1，R=1，Q=2，ε =1)Fig.2 Guidance gains NP1 and NE1(d=0.1，R=1，Q=2，ε =1)

3.3 对策空间分析

将式(36)两边微分，并代入式(31)和(32)可得

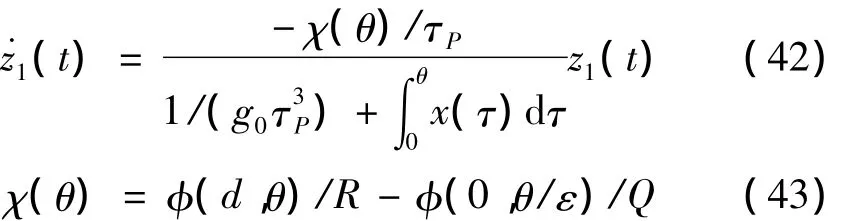
假设初始条件已知，求解z1(t)，可表示为

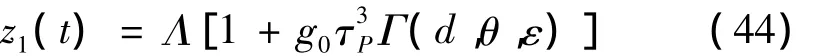
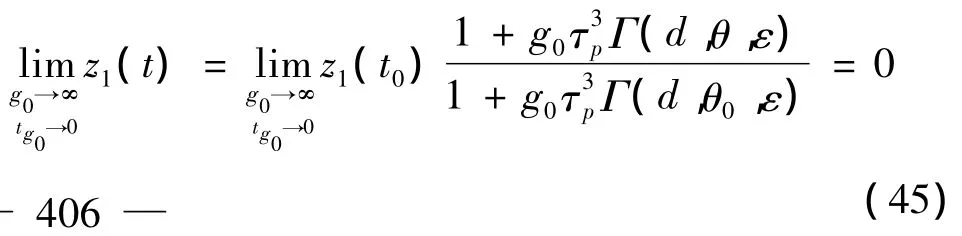
当g0＜∞时，z1(t)是一个与初始条件相关的非零值:

较大的g0值有助于目标的拦截，但也会增加导弹在拦截末端的机动性能要求，如图2(a)所示。随着g0的不断增大，导弹制导末端增益随之增大。g0体现了导弹机动性能与目标拦截要求间的设计折中。

则存在共轭点。对于微分对策双方优化问题，共轭点不存在的充分条件是存在鞍点解，而鞍点解当且仅当系统状态方程(4)所对应的Riccati微分方程的解P(t)是有限时才存在[8]:

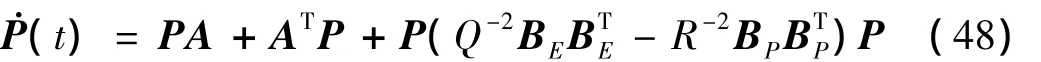
其中，P(tf)=G。而当且仅当制导增益有界时，P(t)才能保持是有限的[9]。进一步由式(47)，可得

由式(39)知，φ(d，η)≥0，f(d，η)是单调增加的，式(49)分母在处取得最大值，而当ε不断增加时，项ε3增加，项 φ(0，τ)dτ减少，因此Q存在最大值。图3为ε∈[0，1]范围内存在共轭时的Q最大值变化曲线，此时目标具有较大的机动动态优势。如图3所示，当近似ε＞0.69时，系统不存在共轭点，且当坐标点(ε，Q)位于曲线上方时，同样也不存在共轭点，如(ε =0.5，Q=2)。

图3 Q最大值随 ε变化曲线(g0→∞，d=0.1，R=1)Fig.3 Relationship between themaximum Q and ε(g0→∞，d=0.1，R=1)

图4(a)为不存在共轭点时的拦截对策空间，对策值收敛到零。图4(b)为存在偶共轭点[10]时的拦截对策空间，该共轭点为对应Q取得最大值时的点，此时式(34)对应的Riccati微分方程的解在该共轭点两边是半正定的，属于鞍点解的特殊情况。图4(c)为存在一般共轭点时的拦截对策空间。

可见，只有当近似θ＜0.68时，才存在最优弹道使得对策值收敛到零。因此，在目标和拦截导弹机动时间常数比一定的情况下，为实现导弹在整个待飞时间段内不出现共轭点，导弹应具有足够的机动性能，即Q/R足够大。为了保证系统不出现共轭点，除了选取适当的参数外，结合式(44)，还可通过取有限的g0值实现，即有限脱靶量情形。图5为g0取有限值时，对于不同初始条件的脱靶量曲线，为保证鞍点解的存在，系统性能被折中。

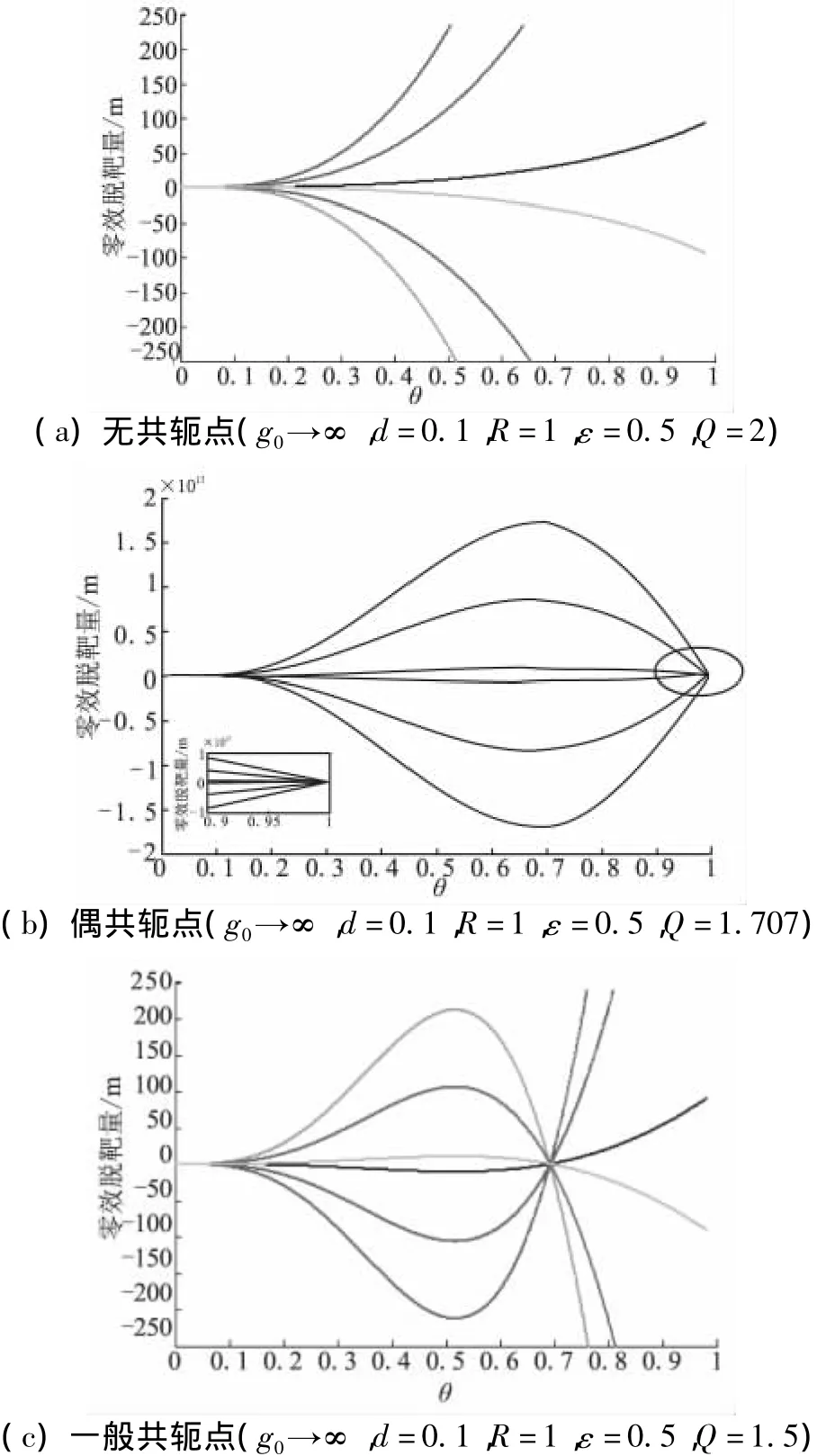
图4 拦截对策空间Fig.4 Intercept game space

4 结束语

基于微分对策双边优化理论，给出了一种可适用于具有任意阶控制的拦截导弹和目标的一般形式线性二次型微分对策制导律。针对一类具有一阶正当传递函数的拦截导弹进行了制导律的推导，给出了解析表达式，并对其制导增益和对策空间进行了分析，在目标和拦截导弹机动时间常数比一定时，为实现对目标的零脱靶量拦截，拦截导弹应保证具有足够的机动优势。同时，仿真结果也验证了该一般形式微分对策制导律。由于只针对弹目相对质心运动模型进行了研究，未就拦截导弹姿态控制回路对制导回路的影响加以考虑，且该部分也属于集成制导与控制的研究范畴，将作为后续基于微分对策制导理论研究的重点。

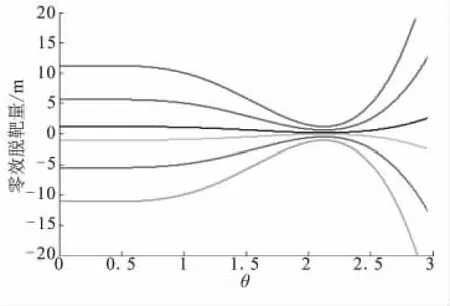
图5 有限脱靶量对策空间(g0=2 000，d=0.1，R=1，ε =0.5，Q=1.5)Fig.5 Finitem iss distance game space

[1] 苏晓丹.飞行器姿态控制系统综合的一种微分对策方法[J].航天控制，2009，27(3):72-75.

[2] 王长青，史晓丽，王新民，等.基于LQ微分对策的最优规避策略与决策算法[J].计算机仿真，2008，25(9):74-78.

[3] 李登峰，罗飞.舰艇编队信息战火力分配微分对策模型及求解[J].控制理论与应用，2008，25(6):1163-1166.

[4] 马礼举，魏志鹏.基于目标姿态信息的导弹微分对策制导律研究[J].弹箭与制导学报，2009，29(3):43-46.

[5] Anderson GM.Comparison of optimal control and differential game Intercept guidance laws[J]，Journal of Guidance and Control，1981，4:109-115.

[6] Ryoo C K，Cho H，Tahk M J.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance，Control and Dynamics，2005，28(4):724-732.

[7] Shafferman V，Shima T.Linear quadratic differential games guidance law for imposing a terminal intercept angle[J].Journal of Guidance，Control and Dynamics，2008，31(5):1400-1412.

[8] Bryson E A，Ho C Y.Applied optimal control[M]，Blaisdell，Waltham，MA，1969，9:282-289.

[9] Ben-Asher JZ，Yaesh I.Advances inmissile guidance theory[M].Progress in Astronautics and Aeronautics，AIAA，Reston，VA，1998，180:25-90.

[10] Bernhard P.Linear-quadratic，two-person，zero sum differential games:Necessary and sufficient conditions[J].Journal of Optimization Theory and Applications，1979，27(1):51-69.