基于RANS/NLAS的火箭跨声速脉动压力环境预示①

任淑杰，张收运，闫桂荣

(西安交通大学航天航空学院，西安 710049)

0 引言

脉动压力又称为气动噪声，在飞行器设计阶段具有重要地位。目前，飞行器表面脉动压力环境的预测主要采用风洞实验和数值计算方法。文献[1－3]均采用风洞实验方法，研究了飞行器表面的脉动压力特性;文献[4－7]分别采用混合 RANS/LES、LES/FWH、LES/APE、LES/Lighthill计算方法，进行了脉动压力环境预示。但风洞实验耗资大，且重复性较差，而现有数值计算方法均采用LES求解流场，LES对计算网格要求很严，造成流场计算耗时。

为实现对飞行器脉动压力环境的快速求解，Morris等人在1996年首次提出了一种采用雷诺平均N-S方程(RANS)求解流场，再采用非线性噪声求解方程(NLAS)求解声场相结合的混合方法，并用于超声速来流三维轴对称喷流噪声的预示，但忽略了粘性扰动项的影响[8]。Batten等人在2002年进行了改进，考虑了粘性扰动项的影响[4，9]，并用于汽车后视镜和密封腔气动噪声的预测。此方法采用RANS求解流场，使得流场的计算网格较LES更稀疏，节约了计算资源，缩短了计算时间，但尚未用于大型结构的脉动压力环境预示研究。

对于大型火箭结构，跨声速阶段的脉动压力环境相当严重，且有明显的低频峰值信号。低频脉动压力可能与火箭箭体结构低阶模态接近，进而导致火箭箭体结构的疲劳甚至破坏。因此，准确预测火箭表面的脉动压力，对火箭结构安全至关重要。

然而，直接将改进的RANS/NLAS方法用于大型火箭结构的脉动压力环境预示时，由于火箭结构尺寸较大，会造成流场和声场求解区域较大。在实际计算时，难免遇到计算量大、计算时间长的问题。此外，要精确描述NLAS方程中的非线性项，进行RANS方程求解时，需采用一种考虑非线性的湍流模型。

针对这些关键问题，本文采取如下技术方案:削减了部分远场计算区域，将远场设置为吸收边界，以消除远场边界反射;减小了近壁网格尺度，并采用壁面函数法求解壁面区域，以提高壁面计算精度;选用两方程非线性k-ε湍流模型，以精确求解NLAS方程的非线性项;最后，进行了大型火箭跨声速脉动压力环境的预示研究，计算结果较好地反映了火箭所处的脉动压力环境，为火箭跨声速脉动压力环境预示提供了一定的参考依据。

1 控制方程和数值计算方法

NLAS的控制方程是从Navier-Stokes方程导出的，它将每一项分成统计平均项和扰动项2部分，即φ=¯φ+φ＇。代入Navier-Stokes方程，并重新安排扰动项和平均项，得到非线性扰动方程组[8－9]:

式中Q＇是瞬态扰动项是瞬态平均项;F＇i是线性无粘扰动项;F＇ni是非线性无粘扰动项;是无粘平均项;是粘性扰动项;是粘性平均项。

具体表达式如下:

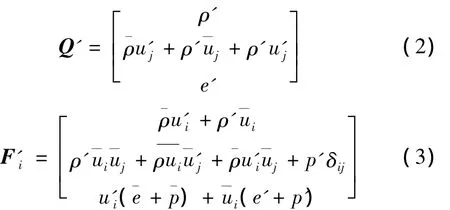
式中 ρ是密度;ui(i=1，2，3)是x、y、z3 个坐标轴方向的速度;p是压强;e是单位体积能。

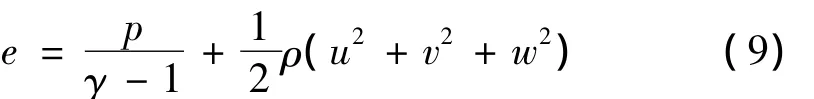
剪切应力项

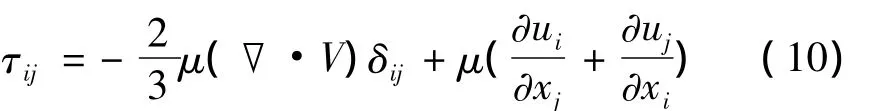
热传导项

RANS控制方程采用有限体积法求解，无粘项采用二阶精度TVD格式离散，粘性项采用中心差分格式离散，时间推进选用隐式方法。湍流模型选用两方程非线性k-ε湍流模型，以精确求解NLAS方程的非线性项。远场边界给定来流的压强p∞、温度T∞、速度u∞。NLAS控制方程采用有限差分方法求解，时间推进也选用隐式方法。远场边界为RANS求得的平均流场信息。

流场物面第1层网格尺度设置为2×10－5，声场物面第1层网格尺度设置为10－4，物面边界均采用粘性无滑移绝热壁，并应用壁面函数法求解，以保证物面区域求解精度。远场计算区域均为火箭长度的5～10倍，并设置为吸收边界，以消除远场边界反射。

2 计算结果及其分析

2.1 计算模型

计算了以锥柱-船柱-裙柱为基本外形的火箭表面的脉动压力，自由来流马赫数分别为 0.8、0.825、0.85、0.875、0.9、0.925、0.95、0.975、1.025、1.075、1.1、1.125、1.15、1.175、1.2。图1 给出了火箭几何外形简图，并记火箭表面6 个转折点为A、B、C、D、E、F。

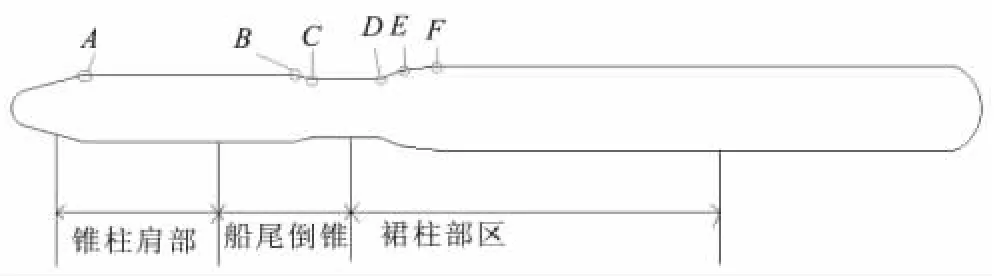
图1 火箭几何外形简图Fig.1 Schematic diagram of rocket

图2给出了锥柱肩部脉动压力系数计算曲线，并与文献[10]中的曲线进行了对比。由图2可知，计算值和文献值基本吻合。

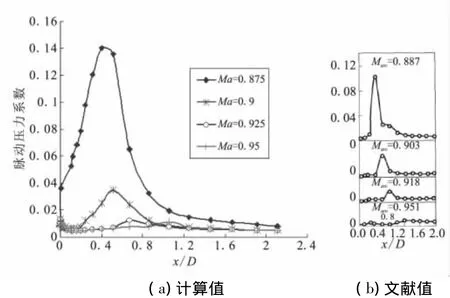
图2 锥柱肩部脉动压力系数Fig.2 Fluctuating-pressure coefficient of cone-cylinder

2.2 脉动压力产生机理分析

脉动压力环境与飞行器表面的基本流动状态密切相关。经分析速度矢量图(图3)和压强云图(图4)可知，跨声速阶段，锥柱肩部和裙柱部区的气流始终未发生分离，这是因为气流是否发生分离与半锥角、裙压缩角、裙前柱长度等密切相关;来流Ma≥0.875时，船尾倒锥区的气流发生分离，Ma=0.975时，气流分离最严重。

锥柱肩部和裙柱部区的脉动压力是由转折点附近的激波振荡引起的，船尾倒锥区的脉动压力主要是由转折点附近的激波振荡与绕流分离再附体相互作用引起的，且此时形成更加强烈的脉动压力。

2.3 锥柱肩部脉动压力

跨声速阶段激波处于不稳定状态。随着来流马赫数增加，激波后移，强度减弱，激波前后压强差减小，由激波振荡引起的脉动压力也就相应地减小，这从图5锥柱肩部脉动压力系数随马赫数增加峰值后移、幅值减小可看出。从脉动压力系数量级上，可发现锥柱肩部产生抖振的马赫数范围是0.8～0.9，具有强局部特性，马赫数大于0.9之后，脉动压力系数曲线虽有峰值，但量级很小。

图3 船尾倒锥区速度矢量图Fig.3 Velocity vector of inverted cone

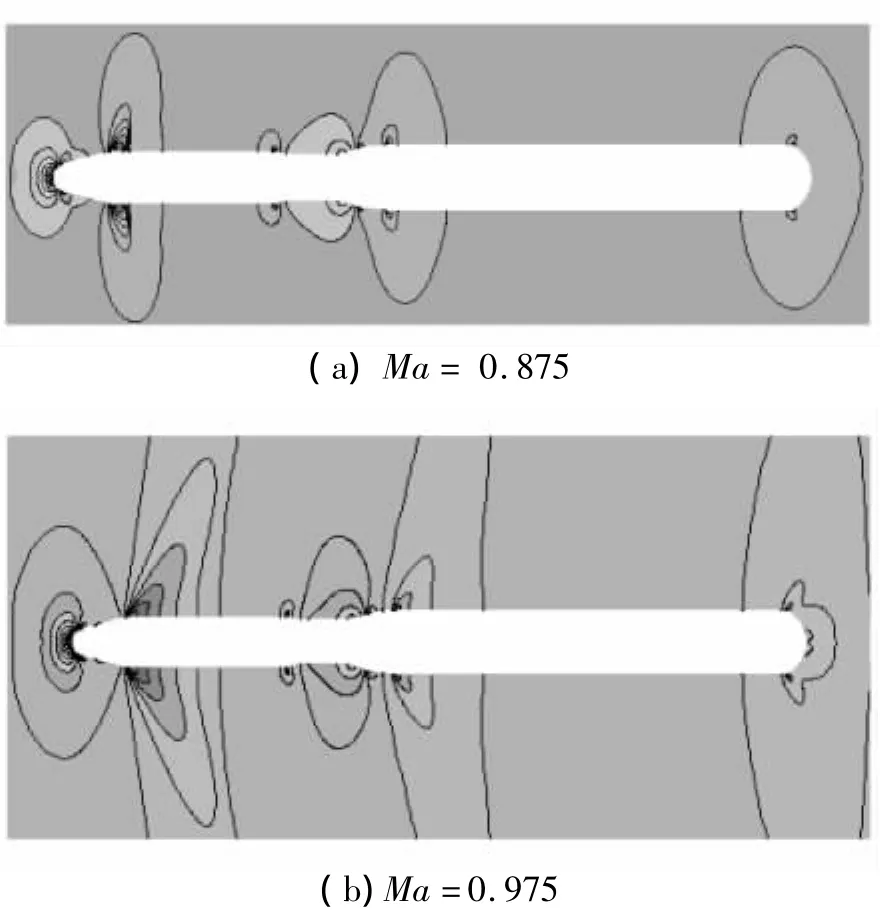
图4 压强云图Fig.4 Pressure contours of rocket

2.4 船尾倒锥脉动压力

对于各种实际类型的分离流场，其再附体点比分离点产生更大一些的脉动压力[10]。然而，当分离流动和激波振荡相互作用时，这个结论就不再适用，而是与来流马赫数密切相关。

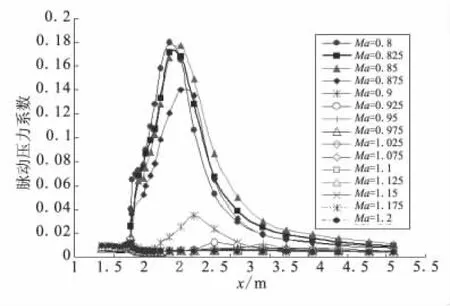
图5 锥柱肩部脉动压力系数曲线Fig.5 Fluctuating-pressure coefficient of cone-cylinder

来流马赫数为0.8～0.85时，船尾倒锥区的脉动压力主要由转折点B、C附近的激波振荡产生，且转折点B处的脉动压力系数比转折点C处的要高。

来流马赫数为0.875～1.075时，船尾倒锥区脉动压力主要由激波振荡和流动的分离再附体相互作用引起。来流马赫数为0.875时，由于气流刚开始分离，分离对脉动压力的影响小于激波振荡的影响，分离点的脉动压力系数仍高于再附体点;来流马赫数为0.9～0.975时，分离对脉动压力的影响和激波振荡的影响比重相同，分离点和再附体点的脉动压力系数大小基本一致，此时脉动压力环境最为严重;来流马赫数为1.025～1.075时，分离对脉动压力的影响大于激波振荡的影响，分离点脉动压力系数明显低于再附体点。来流马赫数为1.1～1.2时，分离点后移速度加快，分离点未和转折点B附近的激波振荡相互作用，以致形成3个脉动压力峰值:第1个是由激波振荡引起的;第2个是由分离点引起的;第3个是由再附体点和激波振荡相互作用引起的。

2.5 裙柱部区脉动压力

裙柱部区的脉动压力主要是由转折点D、E、F附近的弱激波振荡引起的。来流马赫数小于1时，E点附近激波强度最大，相应的脉动压力系数也就最大。来流马赫数大于1之后，E点附近的激波迅速衰减，D点附近的脉动压力系数最大。因此，马赫数为0.8～1.0时，裙柱部区脉动压力环境最为严重。

观察图5～图7脉动压力系数量级可知，火箭表面脉动压力环境最严重的区域就是船尾倒锥区。

2.6 典型点的声压级频谱

图8给出了Ma=0.975时转折点C、E处声压级的1/3倍频程频谱。由图8可看出，跨声速阶段脉动压力能量主要集中在低频(100 Hz附近)，且在90～100 Hz范围内的声压级最大。C转折点总声压级为164.7 dB，是由绕流分离和激波振荡相互作用产生的，E转折点总声压级为144.3 dB，是由激波振荡产生的。

图6 船尾倒锥区脉动压力系数曲线Fig.6 Fluctuating-pressure coefficient of inverted cone

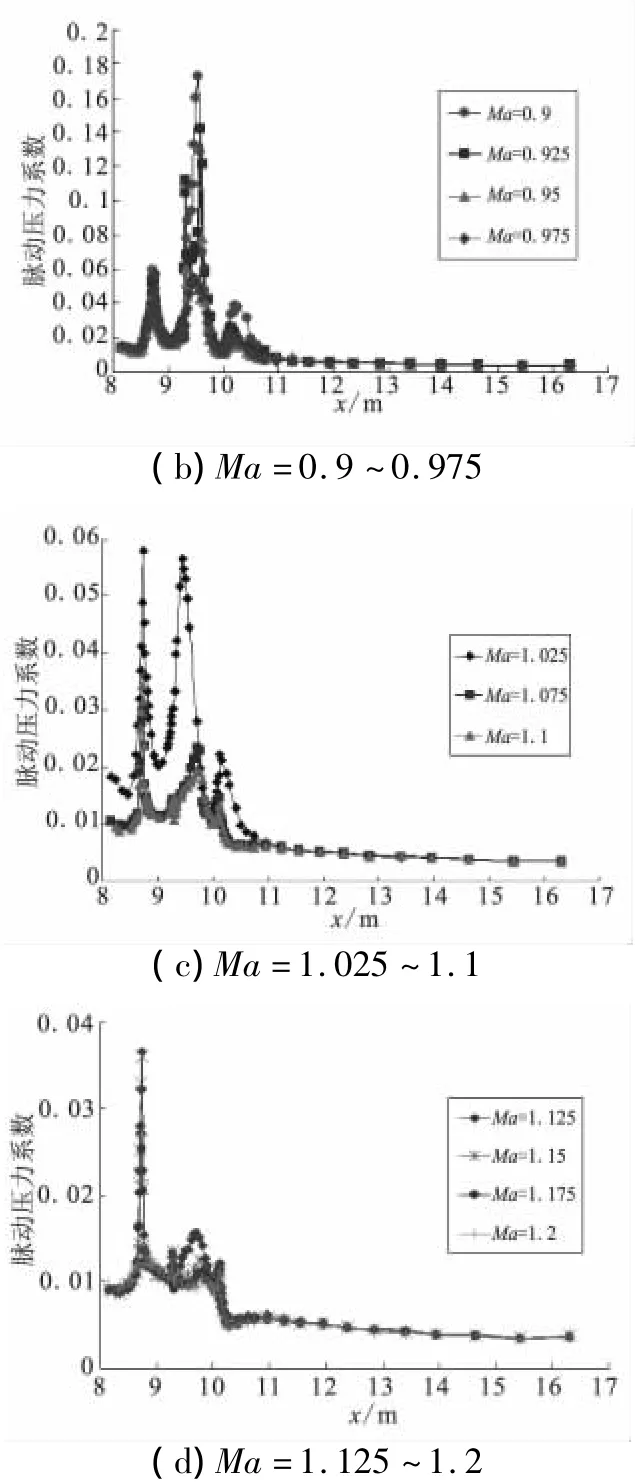
图7 裙柱部区脉动压力系数曲线Fig.7 Fluctuating-pressure coefficient of skirt-cylinder

图8 声压级的1/3倍频程频谱Fig.8 1/3 octave band am p litudes of SPL

3 结论

(1)基于RANS/NLAS，并应用两方程非线性k-ε湍流模型、远场吸收边界及壁面函数法，可成功地进行大型火箭跨声速脉动压力环境预示。

(2)脉动压力环境与飞行器表面的基本流动状态密切相关。锥柱肩部和裙柱部区的脉动压力主要是由激波振荡引起的，船尾倒锥区的脉动压力主要是由激波振荡与绕流分离再附体相互作用引起的。

(3)船尾倒锥区的脉动压力环境比锥柱肩部、裙柱部区更为严重。当马赫数为0.9～0.975时，船尾倒锥区的脉动压力环境最为严重。

(4)传统观点认为，对各种实际类型的分离流场，其再附体点比分离点产生更大的脉动压力。然而，当分离流动和激波振荡相互作用时，这结论就不再适用，而是与来流马赫数密切相关。

(5)在跨声速阶段，脉动压力能量主要集中在低频(100 Hz附近)。

[1] 王娜，高超.弹体脉动压力特征的实验研究[J].实验流体力学，2010，24(1).

[2] 操小龙，罗金玲，周丹杰，等.锥-柱体外形脉动压力及抖振载荷响应研究[J].战术导弹技术，2010(1).

[3] 杨青，李劲杰，杨永年，等.边条翼布局主要参数对其双垂尾抖振响应影响的风洞实验研究[J].西北工业大学学报，2006，24(3).

[4] Paul Batten，UrielGoldberg，Sukumar Chakravarthy.Reconstructed sub-grid methods for acoustics predictions at all reynolds numbers[R].AIAA 2002-2511.

[5] Ali Uzun，Yousuff M Hussaini.Noise generation in the nearnozzle region of a chevron nozzle jet flow[R].AIAA 2007-3596.

[6] Elmar R Groschel，Matthias Meinke，Wolfgang Schroder.Noise prediction for a turbulent jetusing an LES/CAAmethod[R].AIAA 2005-3039.

[7] Rembold B，Kleiser L.Noise prediction of a rectangular jet using large-eddy simulation[J].AIAA 2894-700.

[8] Philip JMorris，Lyle N Long，Ashok Bangalore，et al.A parallel three-dimensional computational aeroacoustics method using non-linear disturbance equations[J].Journal of Computational Physics，1997，133:56-74.

[9] Paul Batten，Enrico Ribaldone，Mauro Casella，et al.Towards a generalized non-linear acoustics solver[R].AIAA 2004-3001.

[10] Robertson JE.The prediction of fluctuating-pressure environments(induced by three-dimension protuberances included)[R].Wyle Laboratories Research Staff ReportWR 71-10，March，1971.