铝镁推进剂固冲发动机两相燃烧数值模拟①
2011-05-03冯喜平周晓斯李进贤
冯喜平,周晓斯,郑 亚,李进贤
(西北工业大学航天学院,西安 710072)
0 引言
固体火箭冲压发动机(固冲发动机)作为一种新型组合动力装置,因其比冲高、推重比大、工作速度范围宽、可实现导弹全程有动力飞行等诸多优点,已成为未来先进动力技术发展的一个重要方向,受到各国的广泛关注[1],固冲发动机燃烧和流动问题是其基本问题,也是该技术发展关键。
目前,国内外对固冲发动机两相燃烧已进行了大量研究。Stowe R A[2]等针对旁侧进气固冲发动机,开展了两相燃烧数值模拟和实验研究,获得了高效燃烧的发动机结构布局和空燃流率。由于颗粒相采用碳颗粒进行模拟,直连实验采用乙烯/空气混合气替代固体燃料,计算结果与实验结果偏差达16%。针对铝镁推进剂,胡建新等[3]进行了补燃室两相燃烧数值模拟,得到了颗粒的分布,还得到了颗粒粒径对燃烧效率的影响规律。
固冲发动机以金属含量非常高的富燃料一次燃烧成分为燃烧剂,以冲压空气为氧化剂,通过二者在燃烧室的燃烧实现能量转换。二次燃烧的组织和燃烧效率是该发动机的关键问题。尽管国内外进行了大量固冲补燃室两相燃烧数值仿真研究,但在探索增强燃烧机理和提高燃烧效率方面,重点为发动机结构设计参数优化和颗粒特性对二次燃烧的影响分析。研究结论对提高燃烧效率方面具有一定的局限性。
作为一种新型燃烧方法,涡旋燃烧技术因其具有提高气流湍流度、增强火焰稳定、改善对流换热和延长燃烧组分在燃烧室中的驻留时间等诸多优点而被广泛应用。同时,也为固冲发动机两相燃烧提供了新途径。国外对冲压燃烧室中引入涡旋燃烧进行了较早的探索[4],初步摸清了燃烧室中涡旋燃烧流动参数的分布规律。在国内,董韬等[5]率先开展了旋转进气固冲发动机补燃室燃烧流动数值模拟研究。研究表明,有旋进气状态下,燃料与空气燃烧更为充分。
目前,国内开展的固冲发动机旋转进气二次燃烧研究,一次燃气大多采用纯气相代替。这种假设难以真实反映燃烧室中气-固两相涡旋燃烧流动规律,与真实发动机实际工作状况存在较大差异。针对铝镁推进剂中心进气固冲发动机,本文通过有旋射流进气和无旋射流进气条件下的三维、两相和化学反应流场数值仿真,以燃烧效率为准则,研究旋转进气条件下的补燃室气-固两相燃烧,力争找出提高燃烧效率的途径。
1 物理模型
补燃室结构简图如图1所示。补燃室内径120 mm,长度1 575 mm,喷管长度124 mm,喷管喉径76 mm。空气入口为环形,其中心轴线与发动机补燃室中心轴线夹角30°。一次燃气喷嘴扩张角度45°。
采用在补燃室空气入口与一次燃气入口加装轴向叶片式旋流器的方法,来获得进入补燃室旋转燃气和空气的效果。为表述旋转提高燃烧效率的效果,进气方式分别选择无旋、冲压空气与一次燃气同向及反向旋转这3种工况。计算工况如表1所示。
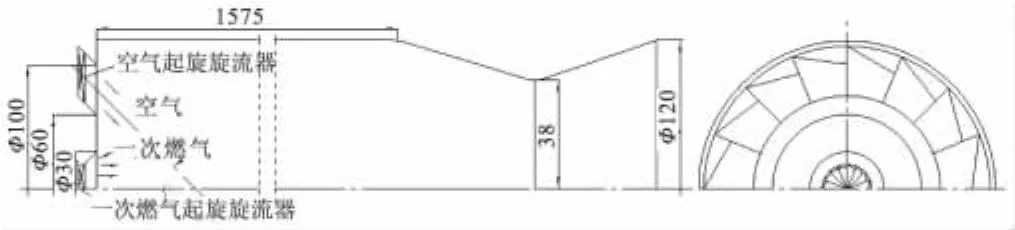
图1 补燃室结构简图Fig.1 Configuration of secondary combustion chamber

表1 计算工况Table 1 Calculation cases
2 基本假设
(1)流动为三维准定常流;
(2)燃气为理想气体,满足理想气体状态方程,p=ρRT;
(3)仅考虑补燃室中铝颗粒蒸发后与氧气的反应,不考虑反应产物Al2O3的破碎、凝结;
(4)凝相颗粒为带有Al2O3薄层外壳包覆的铝颗粒,质量流率为0.02 kg/s,颗粒初始直径均匀分布,为1μm;
(5)在固体壁面上对颗粒采用完全反弹模型,仅考虑气相拖曳力对颗粒的作用,忽略重力、升力等其他作用力及辐射传热对颗粒的影响。
3 数学模型
3.1 圆柱坐标系下的气相控制方程[6]
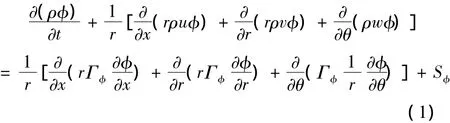
式中 φ 为通用变量,分别为1、u、v、w、T、Cs等变量,分别代表连续方程、动量方程、能量方程和组分方程;Γφ为广义扩散系数;Sφ为广义源项。
3.2 湍流模型
采用Reynolds应力方程模型,对控制方程进行封闭[5]。由于旋转射流湍流流场雷诺应力表现出各向异性的特点,该特点无法采用各种两方程湍流模型进行准确预测。而Reynolds应力方程模型跳过理论根据不够充分的Boussinesq假设,直接模拟湍流雷诺应力输运微分方程,并进行求解。该模型预示的强旋限制性湍流流动特性与实验结果吻合较好[7]。
3.3 颗粒相流动模型
铝颗粒运动采用随机轨道模型[8]:
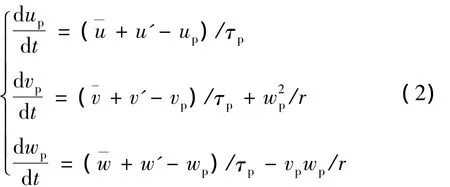
式中up、vp、wp分别为颗粒轴向、径向及切向瞬时速度和u'、v'、w'分别为气相在3个方向上的时均平均速度分量和脉动速度分量;τp为颗粒速度弛豫时间。
3.4 气相燃烧模型
铝镁富燃推进剂一次燃气成分较复杂,一次燃烧产物平衡组分可达数十种。因此,完全详细地模拟补燃室内全部化学反应几乎是不可能的。推进剂性能计算软件进行一次燃气热力计算表明,参与二次燃烧的气相组分主要是CO和H2。一次燃气气相组分中,CO和H2质量分数分别占47%和10%,而CO2和H2O的质量分数均接近1%,其余为惰性组分或微量组分。
依据上述热力计算分析结果,对进入补燃室的一次燃气气相组分进行简化,忽略微量组分,仅考虑主要组分,为 CO、H2、CO2、H2O、N2,质量分数分别为 47%、10%、1%、1%、41%。补燃室内化学反应简化为
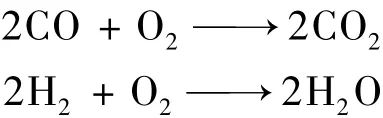
补燃室内气相化学反应采用Magnussen和Hjertager修正的涡耗散模型[5]。该模型反应速率取决于湍流脉动衰减速率,并能自动选择成分来控制速率。因此,能较准确地模拟补燃室内复杂流场的化学反应过程。
3.5 颗粒相燃烧模型
铝颗粒燃烧时,颗粒相与流体之间存在能量和质量交换:
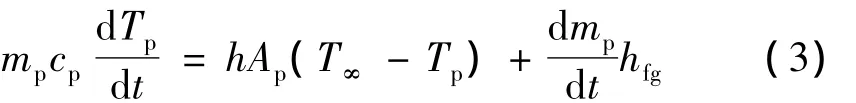
式中mp为颗粒质量;cp为颗粒比热容;Tp为颗粒温度;h为对流换热系数;Ap为颗粒表面积;T∞为气相温度;hfg为颗粒蒸发潜热。
Brooks等人对铝颗粒燃烧的大量实验数据进行分析,提出了与实验现象相符的铝颗粒燃烧时间修正模型[9]。该模型充分考虑了典型环境下氧化剂(H2O、CO2和 O2)浓度、环境压强和颗粒初温等对铝燃烧的影响。本文采用这一修正模型。燃烧时,铝颗粒直径随时间变化为
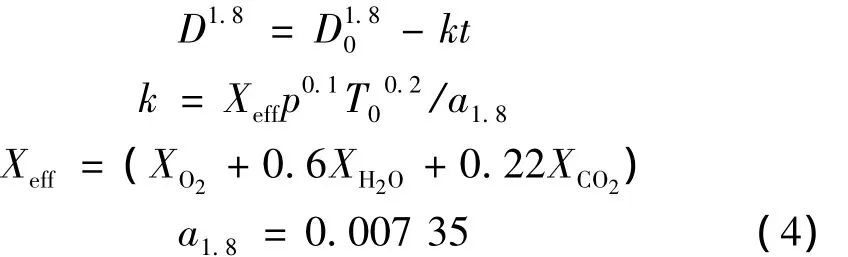
式中D0为颗粒初始直径;D为瞬时颗粒直径;k为燃烧速率系数;X为氧化剂的摩尔分数;p环境压强;T0为颗粒初始温度。
3.6 计算条件
模拟飞行高度1 000 m,模拟马赫数2.2。进气道空气入口流量2 kg/s,总温554 K,总压0.96 MPa;一次燃气入口流量根据空燃比10设计,为0.2 kg/s,总温1 800 K;冲压喷管出口压强0.10 MPa。
3.7 燃烧效率表征
固冲发动机两相燃烧燃烧效率是反映能量转换程度的技术指标,燃烧效率应反映气相和凝相的综合效应。由于燃烧效率主要针对内流场,通过燃烧效率能对发动机二次燃烧组织的优劣及能量转换的高低进行准确评估,可信度更高。文中针对两相燃烧,分别定义气相组分、颗粒以及总燃烧效率,并进行计算。
某一截面气相组分燃烧效率ηg:
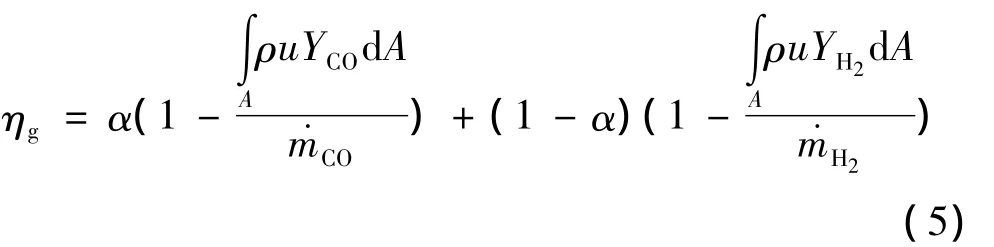
式中YCO、YH2分别为该截面上CO和H2的质量分数;分别为CO和H2的质量流率;α为可燃燃气中CO的质量百分比
某一截面铝颗粒燃烧效率ηAl:

式中为铝颗粒初始质量流率为任意截面铝颗粒剩余质量流率。
某一截面总燃烧效率η:
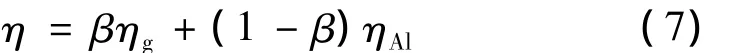
3.8 计算比冲表征
固冲补燃室引入涡旋,除了对补燃效率产生影响外,对发动机的其他性能参数(如比冲、推力等)也同样产生较大影响。由于补燃室中燃气的涡旋运动具有切向分速度的特点,该分速度有可能带来发动机喷管出口排气轴向动量的减小,继而导致发动机推力及比冲的下降。由于发动机比冲是综合评定发动机推力室工作质量的重要性能参数,为了分析涡旋射流对发动机综合性能的影响,本文根据数值仿真结果,对3种工况下的发动机比冲分别进行了计算。
固冲发动机推力:
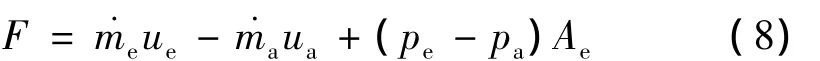
式中a为空气进入进气道时带来的动量;ue为喷管出口排气速度;pe为喷管出口压强;pa为环境压强;为入口空气流率,˙mf为入口燃料流率;Ae为发动机喷管出口面积。
固冲发动机比冲:

4 数值模拟结果及分析
采用流体计算软件Fluent,对发动机补室内两相燃烧流动进行数值模拟。其中,铝颗粒燃烧模型通过用户自定义函数(UDF)进行编程开发,以实现对颗粒燃烧特性的准确数值模拟。
不同工况下铝颗粒平均粒径沿补燃室轴向变化规律如图2所示。由图2可见,当冲压空气与一次燃气以旋转射流方式进入补燃室时(对应于同旋和反旋这2种工况),颗粒粒径减小的速度和程度显著提高。这主要是由于旋转进气涡旋流场下的铝颗粒与气相组分之间混合及相互扩散强度高于无旋射流,气-固之间热量传递的加强以及颗粒与氧气、气相燃烧产物(H2O和CO2)之间混合均匀度的提高,均使得颗粒消耗速率明显加快。铝颗粒燃烧效率沿补燃室轴向变化趋势如图3所示。
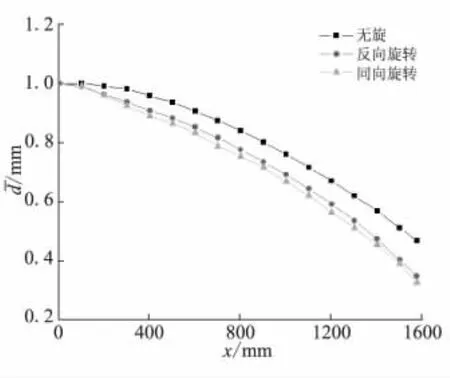
图2 铝颗粒平均粒径沿补燃室轴向变化Fig.2 Change of alum inium average particle diameter alongsecondary combustion cham ber axial direction
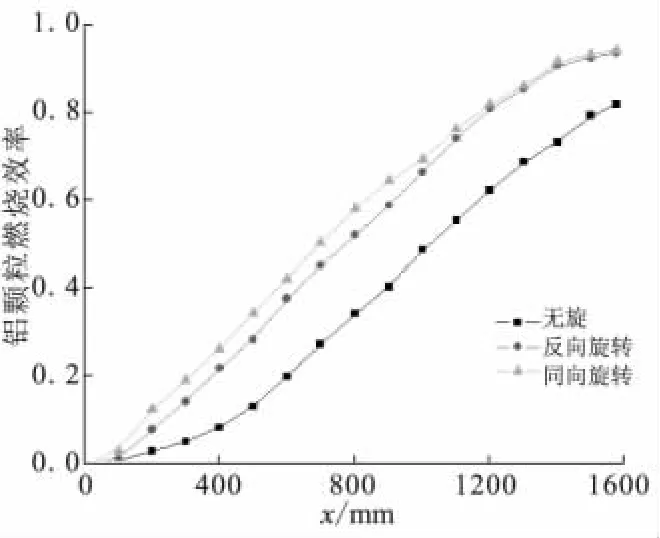
图3 铝颗粒燃烧效率Fig.3 Combustion efficiency of alum inium particle
由图3可见,有旋进气工况下(同旋和反旋)颗粒燃烧效率均高于无旋进气工况,表明颗粒在此工况下能更加快速、完全地燃烧。其原因是一方面,涡旋使得补燃室内可燃气相组分与空气的混合速度变快,气相组分能更加快速、完全燃烧,从而释放出更多的燃烧热,这使得颗粒获得更多的来自气相燃烧释放的热反馈,加快了颗粒的燃烧;另一方面,涡旋增强了颗粒的湍流扩散作用,颗粒能快速弥散在整个气相流场当中,这就加强了颗粒相与气相之间的对流换热效果。同时,与无旋流场相比,有旋流场使得颗粒在补燃室内的停留时间延长,从而相应延长了颗粒的燃烧时间。
由同向旋转与反向旋转工况下颗粒燃烧效率对比可见,在补燃室前段,同向旋转工况下的颗粒燃烧效率要高于反向旋转工况;在补燃室末段,2种工况下的颗粒燃烧效率基本相同,同向旋转略高于反向旋转。其原因是同向旋转工况与反向旋转工况相比,同向旋转工况下两股射流形成的旋流速度要高于反向旋转工况,这使得颗粒在补燃室前段的掺混速度更快,掺混效果更充分。因此,在补燃室前段,同旋工况下颗粒的燃烧完善程度要好于反旋工况。
反向旋转工况下颗粒燃烧效率在补燃室末段逐渐与同向旋转工况趋于相同。这主要是由于随流场向下游发展,反向旋转工况下2股射流在补燃室后段的相互作用更强,这一流场特性已得到了数值计算与实验数据的相互验证[10],射流相互作用的增强同样强化了气-固两相之间的相互作用,这使得颗粒燃烧强度获得提高,从而提高了后段的燃烧效率。铝颗粒质量变化见图4。
表2列出了不同工况下补燃室出口截面燃烧效率和颗粒滞留时间的计算结果。颗粒滞留时间定义为颗粒从进入补燃室到离开补燃室出口截面的最大时间。
由表2可见,当冲压空气和一次燃气以同向旋转方式进入补燃室进行混合燃烧时,补燃室出口截面总燃烧效率最大,而无旋时最小。相对于无旋工况,同向旋转时的总燃烧效率可提高约10.02%;颗粒滞留时间在同向旋转工况时最大,无旋时最小。相对于无旋工况,同向旋转时的颗粒滞留时间可延长约0.699 ms。表3列出了不同工况下发动机比冲计算结果。
由表3可见,当冲压空气与一次燃气以旋转射流方式进入补燃室时(对应于同旋和反旋这2种工况),发动机计算比冲均小于无旋进气工况。由前面对燃烧效率的分析可知,涡旋流场能有效增强一次燃气同冲压空气的掺混,提高燃烧强度。然而,这种增强燃烧的效果不足以补偿因涡旋带来的喷管出口排气轴向动量损失,继而导致了发动机比冲值下降。由同旋和反旋2种工况下的比冲值对比可见,反向旋转进气工况下的比冲值要低于同向旋转进气工况。这主要是由于反向旋转进气工况下的燃烧效率要略小于同向旋转进气工况。同时,反旋工况下的补燃室中形成两股射流相互碰撞的流场特性,增大了压强损失。以上因素综合作用,最终导致了反旋工况下的比冲损失要大于同旋工况。旋转射流进气条件下固冲发动机补燃室两相燃烧特性较为复杂,单方面增强燃烧并不一定能提高发动机的整体性能。在涡旋燃烧的组织方面,必须在增强燃烧效果的同时,尽可能减小旋流对发动机性能造成的不利影响,这方面还需做进一步研究。
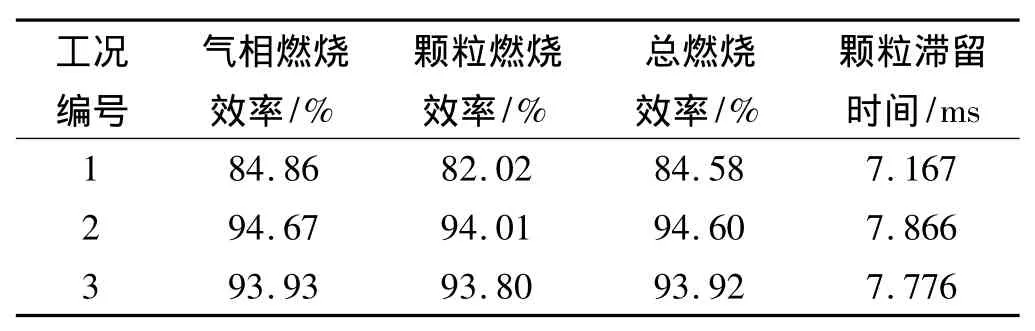
表2 燃烧效率及滞留时间计算结果Table 2 Calculation results of combustion efficiency and residence time
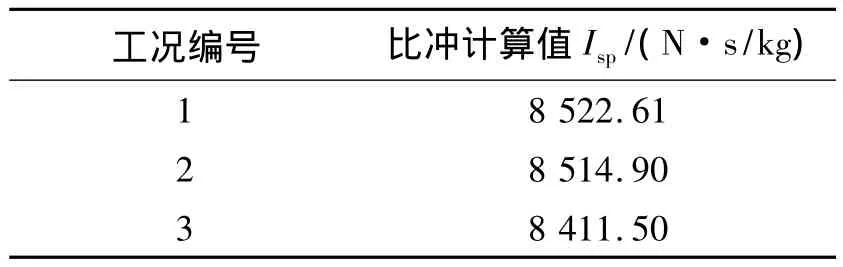
表3 比冲计算结果Table 3 Calculation results of specific im pulse
5 结论
(1)有旋进气工况下(同旋和反旋),颗粒燃烧效率均高于无旋进气,表明颗粒在有旋进气工况下能更加快速、完全地燃烧;
(2)同向旋转与反向旋转工况下颗粒燃烧效率对比情况表明,在补燃室前段,同向旋转工况下颗粒燃烧效率要高于反向旋转工况;在补燃室末段,2种工况下颗粒燃烧效率基本相同;
(3)同向旋转工况下补燃室出口截面总燃烧效率最大,无旋工况时最小。相对于无旋工况,采用同向旋转工况,可使总燃烧效率提高约10.02%;
(4)颗粒滞留时间在同向旋转工况时最大,无旋时最小。相对于无旋工况,采用同向旋转工况时,颗粒滞留时间可延长约0.699 ms;
(5)有旋进气工况下(同旋和反旋),发动机计算比冲均低于无旋进气,涡旋燃烧对发动机性能参数的影响较复杂,采用旋转射流进气必须在增强燃烧效果的同时,尽可能减小旋流对发动机性能造成的不利影响,这方面还需做进一步研究。
[1] 张炜,朱慧,等.冲压发动机发展现状和关键技术[J].固体火箭技术,1998,21(3):24-30.
[2] Stowe R A,et al.Performance prediction of a ducted rocket combustor using a simulated solid fuel[J].Journal of Propulsion and Power,2004,20(5).
[3] 胡建新,夏智勋,刘君,等.非壅塞火箭冲压发动机补燃室两相流数值模拟[J].推进技术,2004,25(3):193-195.
[4] Wu Pei-kuan,et al.Flowfields in a side inlet ducted ramrocketwith/without swirler[R].AIAA 95-2478.
[5] 冯喜平,董韬,等.中心进气旋转射流冲压燃烧室湍流流动数值模拟[J].固体火箭技术,2007,30(3):196-200.
[6] 岑可法,樊建人.燃烧流体力学[M].北京:水利电力出版社,1991.
[7] Hogg S,et al.Computation of highly swirling confined flow with reynolds stress turbulence model[J].AIAA Journal,1989,27(1):57-63.
[8] 赵坚行.燃烧的数值模拟[M].北京:科学出版社,2002.
[9] Beckstead M W.A summary of aluminum combustion[R].ADA 425147,2004.
[10] 张健,尚庆,等.旋流燃烧室内同向和反向旋转射流湍流流动的数值模拟[J].计算物理,2002,19(3):278-282.
