直流脉冲水处理系统感生电流解析建模及激磁线圈优化
2011-04-24韩勇赵永平柴鑫刘小龙
韩勇, 赵永平, 柴鑫, 刘小龙
(哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001)
0 引言
水垢问题一直是困扰锅炉、冷却塔等具有热交换工作过程设备的主要问题,该问题源于这些设备对硬水的使用。直流脉冲水处理器是目前解决水垢问题效果较为理想的电磁场水处理设备,但截至目前,该类处理器阻垢、防垢的机理还没有被人们所掌握,在实际应用中如何根据实际情况对系统进行控制,并使之达到最佳处理效果还缺乏必要的理论指导。目前,有学者猜测,直流脉冲水处理器之所以能起到阻垢、防垢的效果,主要是因为激磁线圈产生的交变磁场在溶液中感生出交变电场,由交变电场对水中的成垢离子进行作用,从而改变了水垢的结晶过程和晶体结构,阻碍了水垢晶体在输水管壁上的附着[1]。国内外有很多学者根据上述对阻垢、防垢机理的猜测,对直流脉冲水处理器的效果做了定性的实验研究[2-7]。由于目前这种只通过实验观察的方法缺乏必要的理论指导,因此对阻垢机理的研究很难深入。虽然直流脉冲水处理器已经被广泛应用,但普遍采用扫频的方式工作,以期望在扫频的过程中有某些频率能符合待处理水体的要求,这同样是缺乏理论指导的表现。因此要想对直流脉冲水处理器的阻垢机理深入研究,就要进行定量研究。
由于溶液中感生出的交变电场是导致水垢离子结晶状态发生变化的直接原因,因此如何精确控制感生电场的强弱是定量研究直流脉冲水处理器阻垢、防垢机理的前提和基础。感生电场的强弱与直流脉冲水处理器激磁信号电压幅值和线圈尺寸参数有关,这些参数通过直接影响线圈内的激磁电流,进而影响激磁电流感生出的变化磁场,并最终影响到变化磁场在溶液内感生出的交变电场。
但截止到目前,尚未有关于直流脉冲水处理系统溶液中感生电流建模及激磁线圈尺寸参数与感生电场作用强度之间定量关系的文献及研究成果发表,因此,本文研究的目的是精确控制溶液中的感生电场,并且为激磁线圈的优化提供理论依据。本文的主要工作为:对直流脉冲水处理系统进行理论建模,推导水溶液中感生电流的表达式,用感生电流的大小衡量溶液中感生电场的大小;同时,推导感生电场在水溶液中做功的平均功率表达式,用平均功率来衡量感生电场对水溶液作用的强弱,并在此基础上建立直流脉冲水处理器激磁线圈尺寸参数与平均功率之间的关系的解析模型。
1 感生电流解析模型
1.1 直流脉冲水处理系统工作原理
直流脉冲水处理器主要由信号发生器及激磁线圈组成,设备工作时,由信号发生器对缠绕在输水管线上的激磁线圈施加高频的直流脉冲信号,由激磁线圈在水管内感应出的交变电场对水溶液进行处理,其结构如图1所示。其中,信号发生单元为激磁线圈提供一定输出功率的方波激励信号,其信号波形如图2所示。
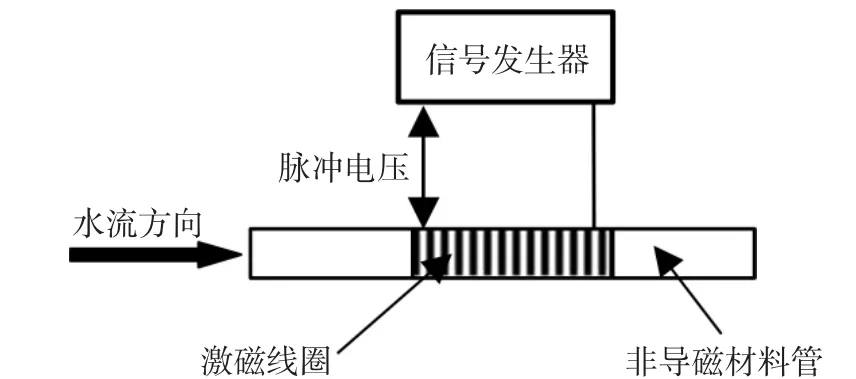
图1 直流脉冲水处理器结构Fig.1 Structure sketch of the DC pulse water processor
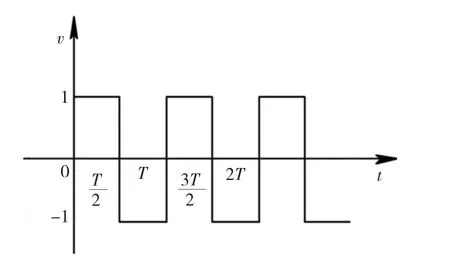
图2 方波激励信号波形Fig.2 Oscillogram of the excitation square wave
在交变的感生电场作用下,溶液中带正电与带负电的矿物质成垢离子分别沿着相反的方向移动,进而增加了正负离子的碰撞几率,并在溶液中形成晶体成长所必须的晶核。当硬水溶液的外部条件发生变化时(如温度升高或压力减小),溶液对水垢分子的溶解度下降,沉淀大量产生,水垢分子开始以溶液中大量晶核为核心,继而晶体在溶液中生长并逐渐形成附着能力较低的沉淀,被水流带走。总之,经过处理后溶液中的沉淀晶体在溶液中生长而不是在水管管壁上生长[1],因此起到了阻垢、防垢的效果。
1.2 溶液中感生电流解析模型
由于溶液中感生电流的大小能直接反应感生电场的强弱,因此本文对感生电流进行建模。由于溶液中的感生电流为环形电流,可以把溶液看作一个单匝线圈[8],本文把激磁线圈与输水管内的水溶液等效为两个同轴线圈组成的系统。在本文研究的直流脉冲水处理系统中,水管材料为塑料。直流脉冲水处理系统的等效电路如图3所示。图3中,i1(t)为激磁线圈电流,R1为激磁线圈电阻,L1为激磁线圈电感,i2(t)为溶液内感生电流,R2为溶液电阻,L2为溶液的电感,M为互感,us(t)为激励方波电压信号。

图3 直流脉冲水处理系统等效电路Fig.3 Equivalent circuit diagram of the DC pulse water processor system
描述图3所示的电路的微分方程组为

对式(1)求解通常较为困难,因此,若要实现用解析方法计算溶液中的感生电流i2(t),需要作如下关键的近似:
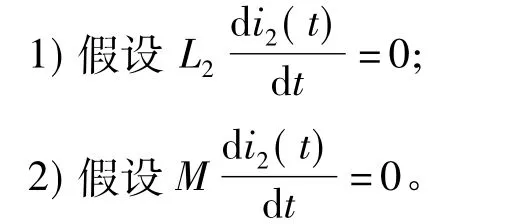
为说明以上假设的正确性,这里,以长为0.1 m,半径为0.02 m,50匝的线圈以及线圈内部圆柱区域的25℃碳酸钙过饱和溶液组成的系统为例,激磁线圈的电感值L1=0.353 4×10-4H,水体的等效电感值L2=0.228×10-8H,互感值 M=K(L1L2)1/2,K 为互感系数,由于溶液被激磁线圈包围,因此可将等效线圈与激磁线圈看做同轴,且耦合较好,又由于在实际中可能存在漏磁等情况,因此本文取K值为0.9,两线圈互感为0.153 5×10-6H,溶液的电阻值R2=438 Ω。由于 L2di2(t)/dt≪R2i2,由式(1)中第二个方程可知,近似 1)成立;又由于 Mdi2(t)/dt≪L1di1(t)/dt+R1i1(t),且感生电流i2(t)的变化率较小,由式(1)中第一个方程可知,近似2)也成立。经过近似后,式(1)变为
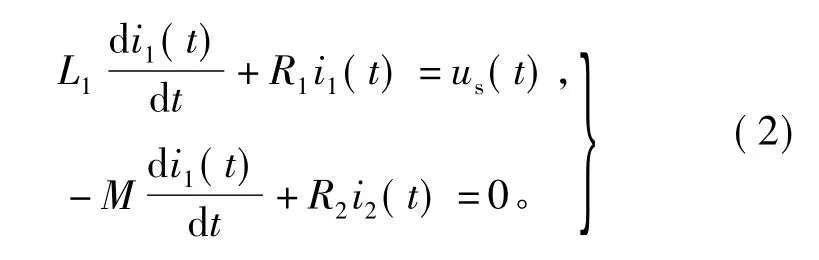
因此,由式(2)中第一个方程可以求得线圈内电流i1(t)的表达式,进而由式(2)中第二个方程计算出感生电流i2(t)。首先求线圈内电流i1(t)的表达式,由于脉冲方波信号us(t)可以看成分段函数,则i1(t)也应采用分段函数的方式表达。
以上述同一线圈为例,将图2所示的方波信号施加至线圈两端,激励信号幅值为1 V,水管内为25℃碳酸钙过饱和溶液,则前6个信号周期内i1(t)的波形如图4所示。

图4 前6个周期的激磁线圈电流波形Fig.4 Excitation current waveform in the first six cycles
当加载的方波激励信号的幅值与频率发生变化时,或激磁线圈的参数发生改变时,图4所示的电流波形的规律同样适用,即图4所示的电流波形特征具有普遍性。
由图4可知,i1(t)的电流波形从第三个周期开始就已经趋于稳定,因此,只需要推导出第三个信号周期i1(t)的解析式,并进一步推导出溶液内感生电流i2(t)的解析式,即可得到后续周期内i1(t)以及i2(t)随时间变化的规律。
图4中第三周期的i1(t)幅值是从点D上升到点E,再从点E下降到点F的过程,并且下降波形与上升波形关于时间轴对称,时间上相差半个周期,因此只需要计算出点D上升到点E的i1(t)表达式,就可以得到i1(t)在完整的第二周期内的表达式。
首先计算A点的电流值,通过式(2)中第一个方程的计算,并考虑初始条件i1(0)=0,可以得到由原点到A点的电流波形的表达式为

仍对式(2)中第一个方程进行计算,并将A点电流看作A点到C点波形的零时刻电流,即该段电流的初始条件为 i1(0)=us(t)(1 - e-T/2τ)/R1,解得由A点到C点的波形表达式为

1.3 感生电场对溶液做功的平均功率与线圈尺寸参数的函数关系
直流脉冲水处理器对溶液处理的过程,从能量转化的角度考虑,可以看作是感生电场的电势能转化为离子动能、碰撞能以及一部分热能等能量的过程。因此,感生电场的电势能越大,则转化成离子的动能、碰撞能以及热能就越多,感生电场对水溶液的作用也就越强烈。为了衡量直流脉冲水处理器在处理溶液过程中感生电场电势能的大小,进而衡量感生电场对溶液作用的强弱,本文选择感生电场在溶液中做功的平均功率P作为衡量标准,平均功率P的表达式为

式中:ρ为线圈绕线材料的电阻率;r0为线圈绕线的半径。将式(15)和式(16)带入式(14)就可以得到平均功率P与线圈匝数及线圈半径的函数关系式。
2 感生电流模型仿真验证
由式(12)可知,平均功率P的解析表达式能否正确地描述感生电场对溶液作用的强弱,完全取决于感生电流i2(t)的解析模型是否正确,即只有感生电流i2(t)的解析模型是正确的,平均功率P的解析表达式才具有实际意义。因此,本文选择用有限元方法验证感生电流解析式的正确性与准确性。由于有限元分析方法对实际模型分析计算的精确度较高,已经得到广泛的应用[10-12],本文对一个确定的直流脉冲水处理器与碳酸钙过饱和溶液组成的系统,分别用有限元方法和本文推导的式(10)与式(11)对感生电流进行计算,将两组计算结果进行对比,从而验证本文推导的感生电流解析模型的正确性与准确性。本文的实际模型如图5所示。
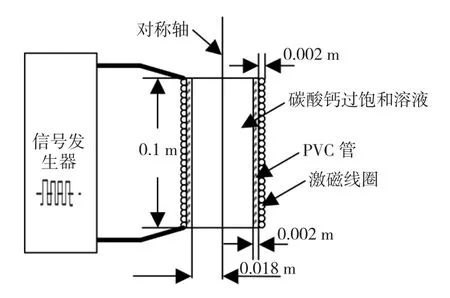
图5 直流脉冲水处理系统的物理模型Fig.5 Physical model of the DC PWP system
图5中,信号发生器内阻很小,可忽略不计,激磁信号频率为500 Hz,幅值为2 V,激磁线圈的绕线材料为铜线,电阻率取25℃时铜的电阻率值1.7×10-8Ω·m,铜线直径为0.002 m,匝数为50匝,线圈为单层密绕,输水管材料为 PVC,管壁厚度为0.002 m,输水管内半径为0.018 m,管内为25℃的碳酸钙过饱和溶液,其过饱和度为1 550.1mol2/L2,电导率为0.78×103μs/cm。通过计算得到激磁线圈的电感 L1=0.353 4 ×10-4H,电阻 R1=0.136 Ω;溶液的等效电感L2=0.228×10-8H,电阻R2=438 Ω;互感 M=K(L1L2)1/2=0.153 55 ×10-6H,K=0.9。将上面得到的各个参数值代入式(10),就可以计算出系统电路进入稳态后,激磁信号的半个周期中任意时刻对应的感生电流值,再根据式(11),就可以得到一个周期内任意时刻对应的感生电流值。
采用有限元方法计算溶液中的感生电流时,由于水管、激磁线圈和碳酸钙过饱和溶液都是圆柱形且对称轴重合,并且所加的激励信号为脉冲方波信号,因此选用精确度较高的二维瞬态有限元电磁分析方法,对每一个激磁信号周期进行分段计算,半个周期为一个时间段,计算平均分布在每个时间段上的10个时间点对应的溶液感生电流。由于所加载的激磁信号频率为500 Hz,则一个时间段为0.001 s,为保证感生电流计算结果是在电路稳态时得到的,需要计算前12个激磁信号周期内的溶液感生电流,取第12个周期的感生电流计算结果与根据式(10)和式(11)计算的结果进行对比,以此验证溶液感生电流解析模型的正确性和准确性。采用两种方法计算的结果如表1所示,表1的数据拟合曲线如图6所示。
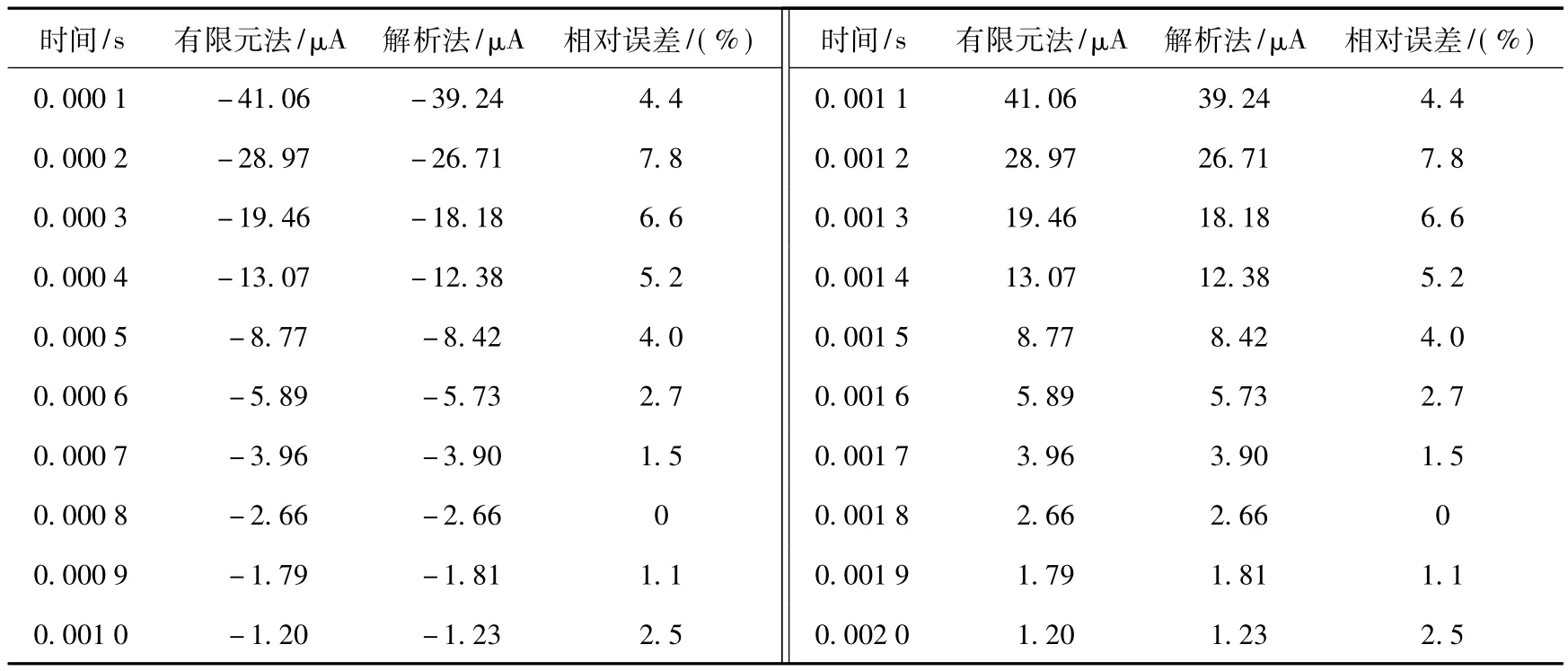
表1 有限元法与解析法计算的感生电流值Table 1 Induced current numerical calculated with finite element method and analytical method
由表1的两组数据对比及图6的数据拟合曲线 可知,两组数据的最大相对误差为7.8%,平均相对误差为3.58%,在实际应用中均在可接受范围之内。因此,根据式(10)与式(11)计算的一个周期内的感生电流值与采用有限元方法计算的感生电流结果较为吻合,从而证明了本文推导的溶液感生电流解析模型的正确性和准确性。

图6 有限元法与解析法计算的一个周期内的感生电流值拟合曲线Fig.6 Fitting curve of induced current numerical calculated with finite element method and analytical method in one cycle
3 线圈尺寸参数与平均功率关系
由式(14)、式(15)和式(16)可知,平均功率P为线圈匝数n与线圈半径r的函数。由式(15)可知,只有当线圈长度大于或等于线圈直径时,式(15)中的级数项才收敛,因此,在P的关于线圈尺寸参数的函数关系中,匝数n和半径r的取值受到条件nd≥2r的约束。下面仍以图5所示的系统模型为例,对平均功率P与线圈半径r和线圈匝数n的关系分别进行探讨。
在探讨之前,值得注意的是,线圈半径的改变可能会影响溶液电阻R2的取值,因此首先计算图5中的溶液区域在不同半径下的电阻值,用二维有限元方法对溶液电阻进行计算,由于有限元方法计算导体电阻是基于能量原理的,因此计算较为精确。本文取溶液区域半径分别为 0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.1 m,计算后相应的电阻值均为 438 Ω,因此可知,半径在[0.01 m,0.1 m]取值区间上时,溶液电阻R2的取值与溶液区域半径无关。因此在以下的探讨中,溶液电阻R2为常数。
1)平均功率P与线圈半径r的关系
根据约束条件nd≥2r,若线圈匝数被确定,则线圈半径的最大值将被确定。考察线圈匝数n为50、30、20匝时,平均功率P与线圈半径r的函数关系,对应的线圈半径r的取值范围为[0.01 m,0.1 m],[0.01 m,0.06 m],[0.01 m,0.04 m],在不同的匝数下,平均功率P与线圈半径r的关系曲线如图7所示。
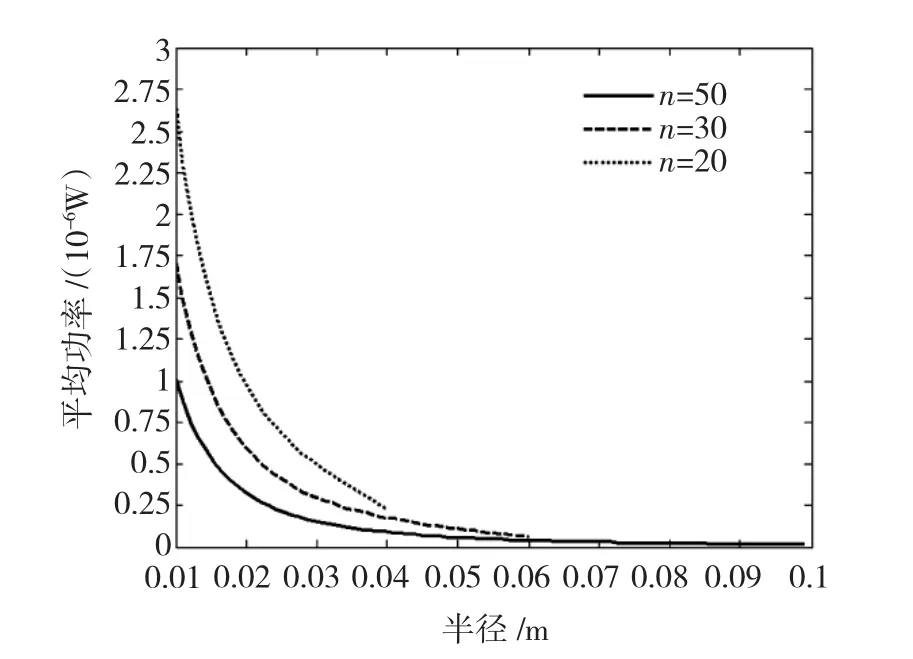
图7 平均功率P与线圈半径r的关系曲线Fig.7 Curve of the relationship between average power P and coil radius r
2)平均功率P与线圈匝数n的关系
根据约束条件nd≥2r,若确定线圈半径,则线圈匝数最小值将被确定。考察线圈半径为0.01、0.03、0.05 m时,平均功率P与线圈匝数n之间的关系,对应的线圈匝数取值范围分别为[10,150],[30,150]和[50,150]。在不同半径下,平均功率 P与匝数n的函数关系曲线如图8所示。
从图7和图8中可以看出,平均功率P随着匝数的增加和半径的增大而减小,若要得到较大的平均功率,应尽量减少激磁线圈匝数和线圈半径。特别是在输水管半径确定的前提下,当匝数取最小值时,即线圈长度等于线圈直径时,平均功率达到最大值。在实际的工程应用中,当直流脉冲水处理系统的信号发生器输出参数确定后,应根据实际处理的水质参数来确定线圈的匝数和半径,通过控制线圈的尺寸来控制直流脉冲水处理系统对水溶液作用的强弱,从而提高阻垢、防垢的处理效果。

图8 平均功率P与线圈匝数n的关系曲线Fig.8 Curve of the relationship between average power P and coil turns n
4 结论
本文建立了直流脉冲水处理系统的数学模型,并在该数学模型基础上,得到稳态时的激磁线圈电流表达式和溶液中感生电流的解析表达式。
此外,用感生电流对水溶液做功的平均功率来衡量感生电场对水溶液作用的强弱,得到感生电流对水溶液做功的平均功率的解析表达式,并进一步研究了激磁线圈尺寸与平均功率之间的关系曲线,通过探讨可知:
1)当线圈匝数为常数,仅改变线圈半径,平均功率与线圈半径的关系为,较小的线圈半径能得到较大的平均功率,反之,较大的线圈半径能得到较小的平均功率。
2)当线圈半径为常数,仅改变线圈匝数,平均功率与线圈匝数的关系为,较少的线圈匝数能得到较大的平均功率,反之,较大的线圈匝数能得到较小的平均功率。在线圈长度等于线圈直径时,平均功率达到最大值。
本文提出的模型及评价方法为直流脉冲水处理器在实际工程应用中阻垢、防垢效果的优化提供了理论指导,并且为直流脉冲水处理器阻垢、防垢机理的定量研究提供了一定的前提和理论依据。
文中使用了带约束条件的电感表达式,因此得出的部分结论存在一定的局限性,虽然目前也有不受线圈长度与半径比限制的解析式,但一般含有连带勒让德函数,不适合带入平均功率的解析式来研究线圈尺寸与平均功率的关系。文中进行的所有计算都是在溶液电导率不变的前提下进行的,但在实际的实验研究中发现,溶液的电导率会随着处理过程缓慢的变化。因此,在后续工作中将从以上两个方面进一步完善平均功率与激磁线圈尺寸参数之间的函数关系。
[1] CHO Young I,FAN Chunfu,CHOI Byung Gap.Theory of electronic anti-fouling technology to control precipitation fouling in heat exchangers[J].International Communications in Heat and Mass Transfer,1997,24(6):757 -770.
[2] CHO Young I,CHOI Byung Gap,DRAZNER Bennat J.Electronic anti-fouling technology to mitigate precipitation fouling in plateand-frame heat exchangers[J].International Journal of Heat and Mass Transfer,1998,41(17):2565-2571.
[3] CHO Young I,LIU Rong.Control of fouling in a spirally-ribbed water chilled tube with electronic anti-fouling technology[J].International Journal of Heat and Mass Transfer,1999,42(16):3037-3046.
[4] CHO Young I,FAN Chunfu,CHOI Byung Gap.Use of electronic anti-fouling technology with filtration to prevent fouling in a heat exchanger[J].International Journal of Heat and Mass Transfer,1998,41(19):2961-2966.
[5] XING Xiaokai,MA Chongfang,CHEN Yongchang.Investigation on the electromagnetic anti-fouling technology for scale prevention[J].Chemical Engineering and Technology,2005,28(12):1540-1545.
[6] VAN HULLE Stijn W H,VERGOTE An,HOGIE Joel,et al.Practical assessment of electronic water treatment for the prevention of fouling[J].Chemical Engineering and Technology,2007,30(5):659-662.
[7] CHO Young I,LEE Sung Hyuk.Reduction in the surface tension of water due to physical water treatment for fouling control in heat exchangers[J].International Communications in Heat and Mass Transfer,2005,32(1-2):1-9.
[8] 苏瑞东.一种基于电涡流的电解质溶液电导率测量方法[J].仪器仪表学报,2010,31(3):678-681.SU Ruidong.Electrolyte solution conductivity measurement method based on eddy current detection[J].Chinese Journal of Scientific Instrument,2010,31(3):678 -681.
[9] 丁健.有限长密绕圆柱形螺线管自感系数的精确表达式[J].大学物理,2009,28(5):21-23.DING Jian.The exact expression of self-inductance for a tightly wound cylindrical solenoid of finite length[J].College Physics,2009,28(5):21-23.
[10] KINCAID Thomas G,CHARI Madabushi.The application of finite element method analysis to eddy current nondestructive evaluation[J].IEEE Transactions on Magnetics,1979,15(6):1956-1960.
[11] 邹本贵,曹延杰,王成学,等.单级同步感应线圈炮电枢的磁场-温度场有限元分析[J].电机与控制学报,2011,15(2):42-47.ZOU Bengui,CAO Yanjie,WANG Chengxue,et al.Finite element analysis of magnetic-thermal fields for armature in singlestage synchronous induction coilgun[J].Electric Machines and Control,2011,15(2):42 -47.
[12] 闫照文,苏东林,李朗如,等.基于ANSYS分析的铝电解槽电磁场计算方法[J].电机与控制学报,2005,9(4):326-329.YAN Zhaowen,SU Donglin,LI Langru.et al.Numerical calculations of the 3-D electromagnetic fields of aluminum reduction cells based on ANSYS program[J].Electric Machines and Control,2005,9(4):326 -329.
