一种无刷双馈电机匝数配合的半解析优化方法*
2022-08-31李雨莎王淑红白崟儒
李雨莎, 王淑红, 白崟儒
(太原理工大学 电气与动力工程学院, 山西 太原 030024)
0 引 言
目前风电领域的主流机型为永磁同步电机(PMSM)和双馈感应电机(DFIG)。与之相比,无刷双馈电机(BDFM)由于其拥有变频器容量小,没有电刷和滑环,系统运行的成本低,可靠性高,并有多种运行状态的特点,因此在变速恒频发电以及变频调速领域均拥有广阔的应用前景[1-2]。
BDFM与常规交流电机的不同之处在于其定子上有两套绕组,功率绕组(PW)直接与电网相连,控制绕组(CW)经变频器与电网相连,两套绕组极对数不同,之间没有直接的电磁耦合联系,通过转子进行能量转换。两套绕组匝数的合理配合有利于提高电机各项性能。为了提升电机运行性能,Xiong等[3]根据齿谐波和正弦绕组的原理,提出了一种不等匝双层线圈的设计方法,并通过仿真和试验验证了所提出的转子结构设计方法的有效性。任泰安等[4]基于齿谐波原理提出了一种采用不等匝数同心式转子绕组的BDFM,推导出了适用于各种绕组分布系数的计算方法,并制造了一台新型不等匝数同心式转子绕组的BDFM试验样机。戈宝军等[5]基于齿谐波原理和不等匝绕组理论,提出一种基于混合式转子结构的多跨距复合式的无刷双馈发电机转子设计方案,有效地提高转子导体利用率以及功率绕组的输出功率,并以一台450 kW电机为例具体分析。文献[6]通过改变转子绕组每相有效匝数来改变转子电阻折算值的大小,从而实现与串电阻起动类似的起动过程和效果。文献[7]推导出软起动型绕线式BDFM较为通用的极槽配合选择原则,设计了3种不同结构的功率绕组,通过MATLAB软件对比分析3种不同结构绕组应用于电机软起动时的起动特性并制作样机进行试验验证。综上所述,现有文献大多针对BDFM的转子绕组结构及匝数进行优化设计,而对定子两套绕组匝数配合的研究较少。
目前无刷双馈电机定子两套绕组的匝数选取没有明确的方法,主要依靠大量的有限元仿真或借鉴异步电机的经验,计算工作量大,耗时很长。同时,由于BDFM含有定子两套绕组及转子绕组共三套绕组,与其他类型电机相比,其发热问题更为突出。因此,本文提出了一种以热负荷为优化目标的BDFM定子绕组匝数配合的半解析优化方法:通过公式解析获得满足同一最大功率的所有匝数配合,经解析筛选及有限元仿真的细化筛选分析,最终得到一组最佳的匝数配合。与完全依靠有限元仿真的匝数优化方法相比,该半解析优化方法减少了工作量,节约了优化设计时间与计算资源。
1 定子绕组匝数配合优化
1.1 约束条件及优化目标的解析推导
设BDFM在稳态状态下功率绕组电流为
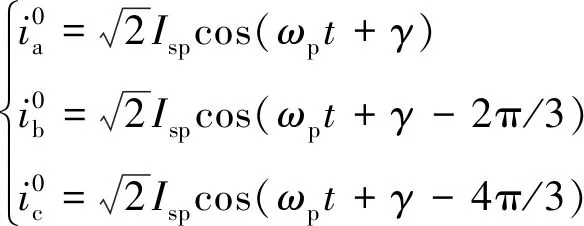
(1)
控制绕组电流为
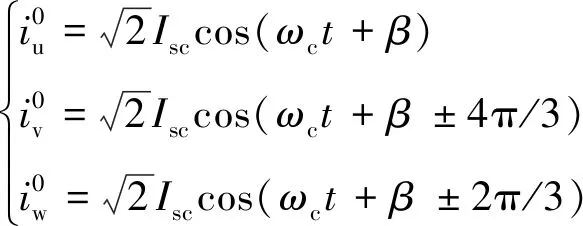
(2)
式中:Isp、Isc分别为两绕组产生电流的有效值;ωp、ωc分别为两绕组旋转磁场电角速度;γ、β分别为两绕组电流初相角,超同步运行时取“+”,亚同步运行时取“-”。
以超同步运行状态为例,两套绕组建立的气隙磁场转换到转子坐标系下为

(3)
式中:Bspm、Bscm分别为两绕组产生的气隙磁密幅值;ω为转子电角速度;pp、pc分别为两绕组极对数;α为功率绕组A相与控制绕组U相的夹角;θ为转子坐标系下位置;ε为功率绕组A相与转子一号嵌套单元轴线的夹角。
定转子角度关系如图1所示。
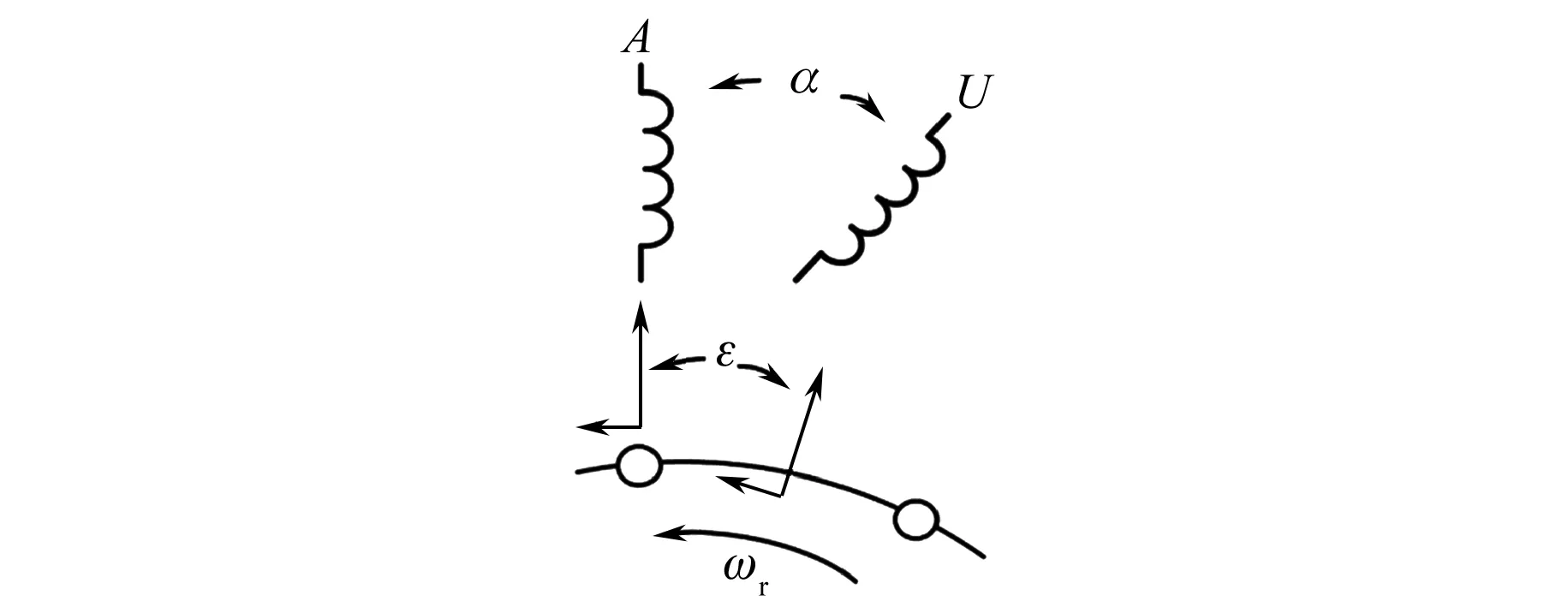
图1 定转子参考系位置关系
在忽略转子短路环电阻的情况下,由磁通连续性定理可知,每个短路环匝链的定转子磁通大小相等方向相反,对转子坐标系下转子电流产生的磁场进行傅里叶分解,得到其pp次磁密分量为[8]
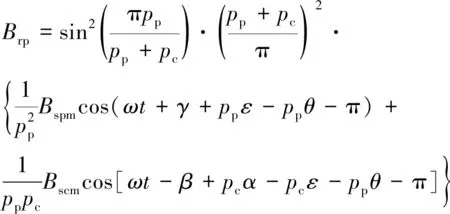
(4)
pc次磁密分量为
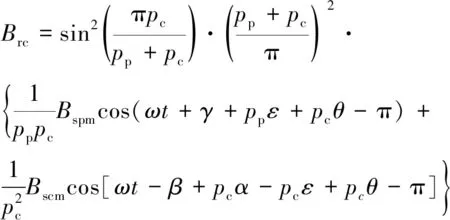
(5)
转子导条可以看作等效绕组,转子磁场即为等效绕组中流过电流所产生的磁场,分析其中一相,则转子产生的A相pp次磁场的等效电流可以表示为
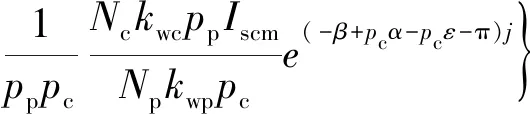
(6)
pc次磁场的等效电流可以表示为
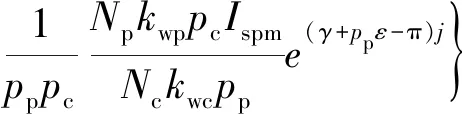
(7)
式中:Np、Nc分别为两绕组每相串联匝数;kwp、kwc分别为两绕组的绕组系数;Ispm、Iscm分别为两绕组电流幅值。
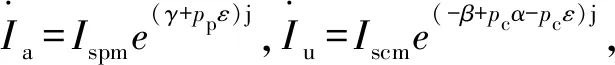
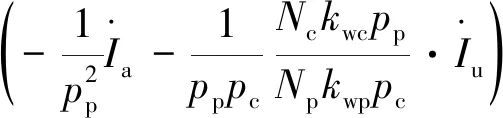
(8)

(9)
忽略定子绕组电阻及漏感,令端电压等于感应电动势:

(10)
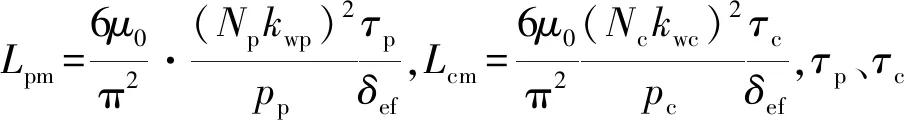
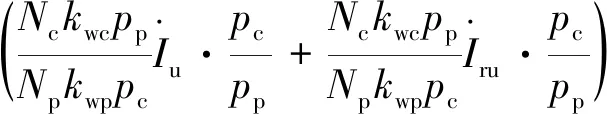
(11)
则式(10)可以进一步化简为
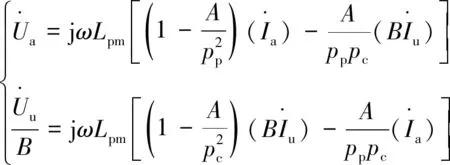
(12)
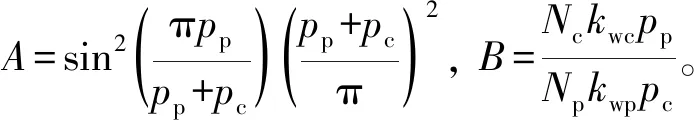
对式(12)解方程组,可得:
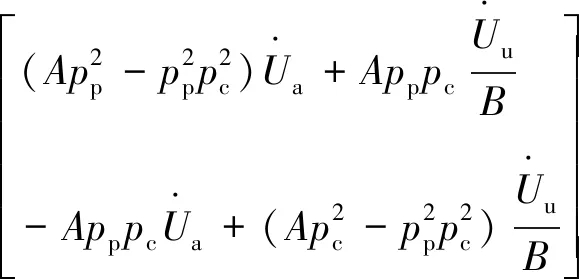
(13)
超同步运行时,定子功率绕组坐标系下电压与转子坐标系下等效电压可以表示为
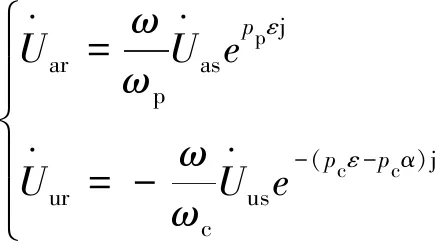
(14)
将式(14)代入式(13),Uar=Ua,Uur=Uu,可得定子绕组电流与电压的关系式:
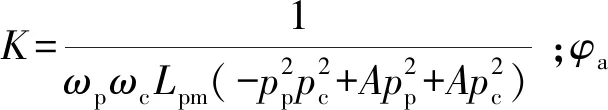
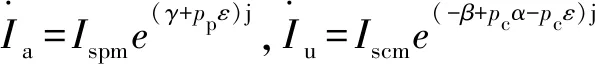
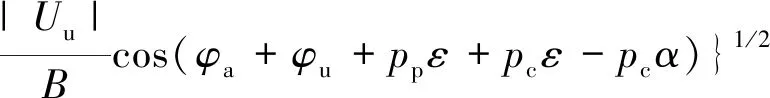
(16)
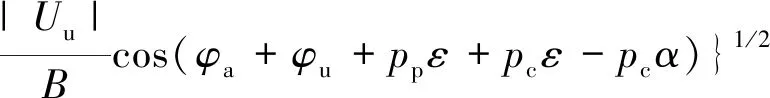
(17)
由式(16)和式(17),可以进一步推导得到超同步运行时BDFM的总电磁功率为[9]
sin(φa+φu+ppε+pcε-pcα)
(18)
电机各角度关系代入后,令φa=0°,则当φu=340°时,BDFM的电磁功率达到最大值,后续理论分析及仿真均在此角度下进行。
热负荷的大小直接影响到电机的发热和温升,热负荷值越大,电机的发热和温升就越高。因此,在电机实际性能优化过程中,希望能在保证输出同样电磁功率的情况下,电机具有尽可能小的热负荷,从而获得尽可能低的温升。
根据热负荷公式,忽略其他谐波磁场,根据式(16)和式(17),BDFM的热负荷可以表示为
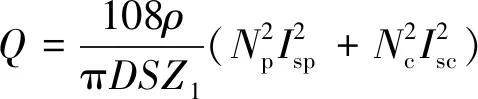
(19)
式中:ρ为导体材料电阻率;D为定子内径;S为定子绕组每槽面积;Z1为定子槽数;Isp、Isc为定子两绕组电流有效值。
对于式(18)与式(19),电磁功率Pe与热负荷Q均是关于Np、Nc的表达式,在匝数优化过程中,保持BDFM的结构尺寸、绕组型式、各角度关系、定子绕组槽满率和电压规格等各项参数均不变,则最大电磁功率是仅关于定子绕组匝数Np、Nc的二元函数,即优化设计变量仅为Np、Nc。同样后续进行有限元仿真时,电机结构尺寸等各项参数均不变,仅每相串联匝数改变,从而保证了匝数优化前后的可对比性。
优化过程中,以最大电磁功率一定为约束条件,以Np、Nc为优化设计变量,可以得到满足同一最大功率的所有匝数配合,以热负荷最小为优化目标,通过理论与仿真的多次筛选与分析,最终在大量满足约束条件的匝数配合中选出一组热负荷最小的匝数。
1.2 求解满足约束条件的匝数配合
以未经过匝数优化的Y280 BDFM为例进行分析,模型基本参数如表1所示,有限元模型如图2所示。
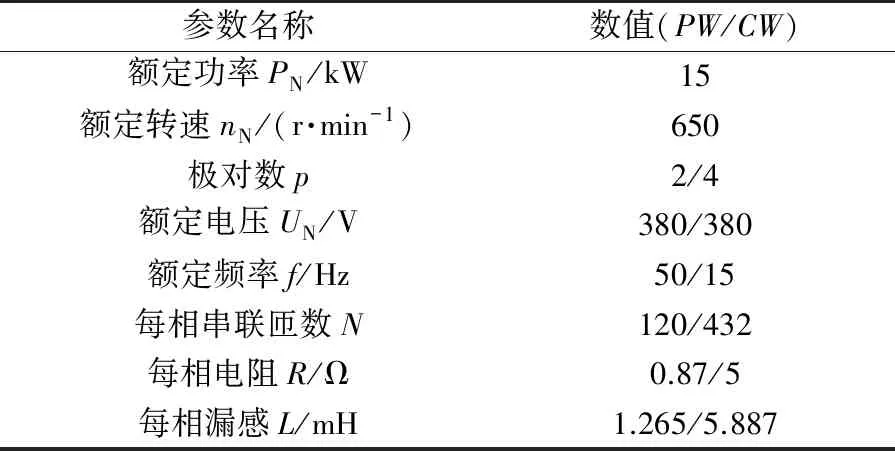
表1 Y280 BDFM模型基本参数

图2 Y280 BDFM有限元模型
式(18)可以简单表示为Pemax=f(Np,Nc),做出最大功率与Np、Nc的函数图如图3中的黑色曲面所示,将电机的功率约束值也画在同一函数图中,即图3中的功率给定值。两曲面的交线即为满足该最大功率约束条件下的所有匝数配合,即交线上的每一组匝数配合均可以保证电机具有理论上相同的最大电磁功率。由于满足约束条件的匝数配合众多,此处不便一一列出。
1.3 排除不合实际的匝数配合
首先,为保证优化前后的可对比性,以及满足电机的实际运行要求,合理匝数配合应满足以下条件:
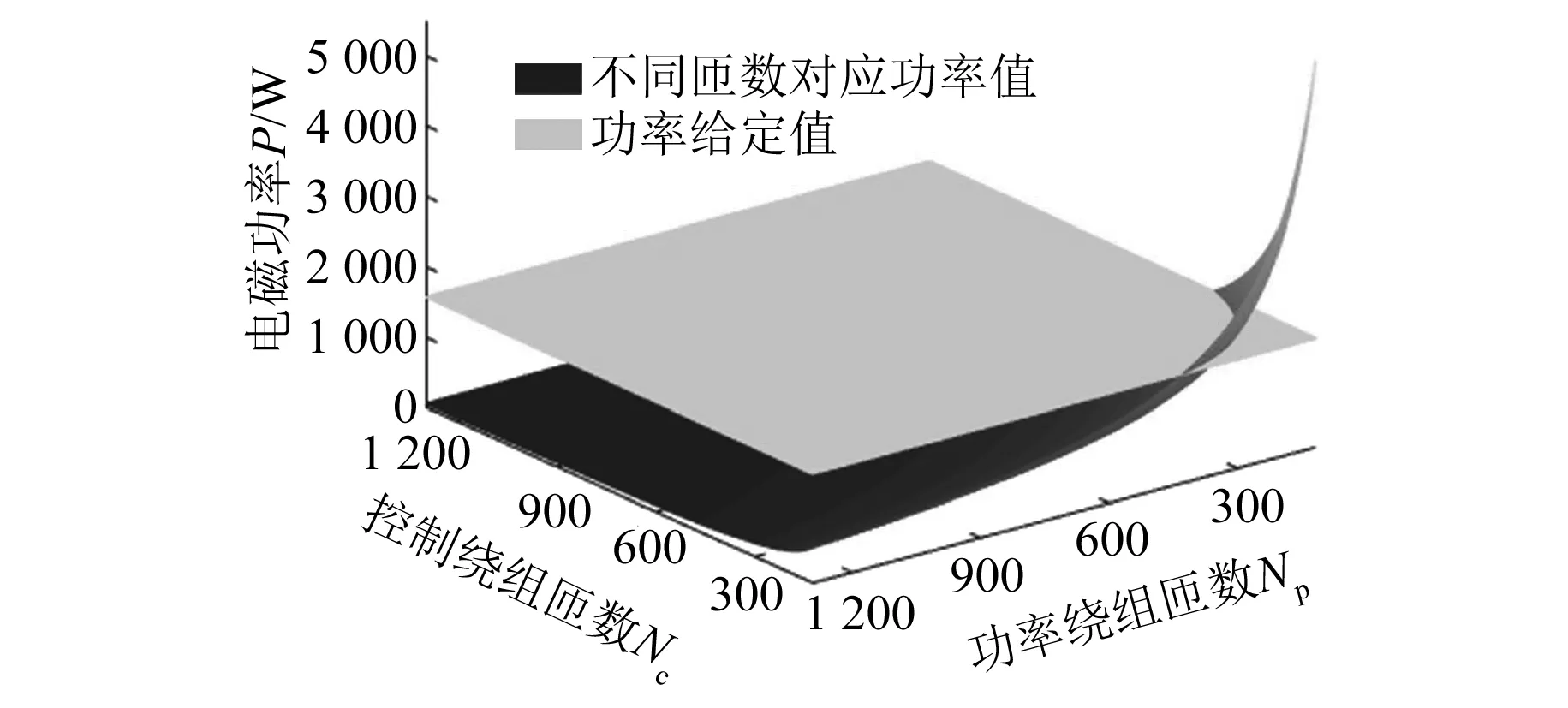
图3 两套绕组匝数变化时的电磁功率
(1) 不改动电机外形尺寸的情况下,绕组匝数可以放入原电机模型,保证绕组型式、节距等与原来一致,不会出现分数槽等问题。
(2) 若存在多条并联支路时,基波旋转磁场在各条支路中产生的感应电动势应保持大小及相位相同,避免各支路间环流问题[10]。
排除不满足上述两个条件的匝数配合之后,剩余匝数配合结果如表2所示。

表2 Y280 BDFM匝数解析结果对比
其次,排除不能使电机正常运行于双馈同步状态的匝数配合。
由表2可见,某些匝数配合下误差很小,某些匝数配合下误差很大,并随着两套绕组匝数差距的增加而偏差增大。以下分析其原因,电机端电压与匝数、频率、磁通之间的关系如下:
U≈E=4.44fNΦ
(20)
将磁通Φ展开,式(20)可以表示为

(21)
式中:B为磁密;l为轴向长度。
当端电压给定时,电机外形尺寸固定,由式(21)可以得到磁密与极对数、频率和匝数的关系式:
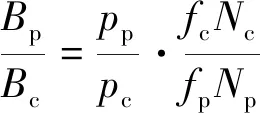
(22)
根据BDFM的基本原理可知,其气隙中包含两种极对数的磁场(pp对极和pc对极),而异步电机气隙中只存在一种极对数磁场。若气隙中两种磁场大小悬殊,则磁场过大的这一极对数磁场将起主要作用,而另一极对数磁场作用微弱,使BDFM运行状态接近异步运行状态,与式(18)、式(19)所推导的双馈同步状态不符,则该组匝数不应选择。
经研究表明,双馈运行时经转子调制后气隙磁场中两种基波磁场比值在0.2~5之间为宜[9]。按照该磁场比值关系进行排除,可以发现,选择范围内的各组匝数配合的解析值与仿真值误差较小,说明该方法在双馈同步状态下可以有效指导匝数优化。
排除不满足上述两个条件的匝数配合,并排除近似异步状态的匝数配合之后,剩余匝数配合结果如表3所示。

表3 Y280 BDFM满足约束条件且符合实际的匝数配合
1.4 通过优化目标筛选
将各组满足约束条件并符合实际的匝数配合(表3中的配合)代入优化目标式(19),可计算得到分别采用这些匝数配合时电机的热负荷值。由于解析过程无法考虑到电机铁心饱和、定转子开槽、集肤效应等各种非线性问题,解析计算结果不可避免会存在一定的误差,因此筛选出优化目标值(即热负荷值)前3组或前5组较小的匝数配合,然后进入有限元仿真的进一步细化筛选,以求避免漏失最优匝数配合结果。
对于Y280 BDFM,经解析方法筛选出热负荷前三小的匝数配合为96/540、108/480和120/432。
1.5 仿真细化筛选
运用有限元仿真软件,对上述筛选出的三组匝数配合进一步细化筛选,选出其中仿真热负荷最小的一组匝数。图4为解析筛选得到的三组匝数,经有限元仿真得到的定子绕组感应电动势与电流波形。表4为根据电流及感应电动势进一步计算得到的电磁功率、热负荷、效率等数据,以及定转子上的各项损耗平均值。由图4和表4可知,匝数配合Np/Nc=108/480是这三组匝数配合中热负荷仿真值最小的,与表3解析结果一致。
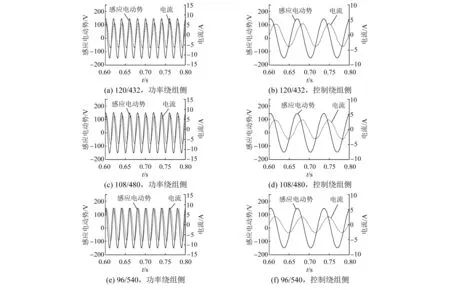
图4 匝数配合细化筛选仿真结果
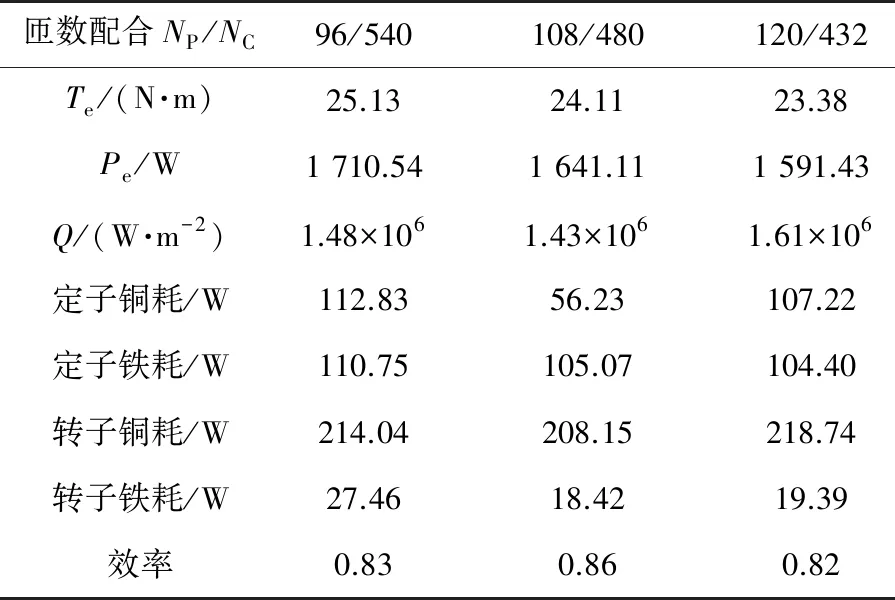
表4 Y280 BDFM匝数筛选细化仿真结果
因此,对于Y280 BDFM,利用本文的匝数配合优化方法,以最大电磁功率一定为约束条件,以热负荷最小为优化目标,最终选取的匝数配合为108/480,该组匝数是满足给定电磁功率条件的大量匝数配合中热负荷最小的一组匝数,可以称为最优匝数,新旧匝数性能对比如表5所示。
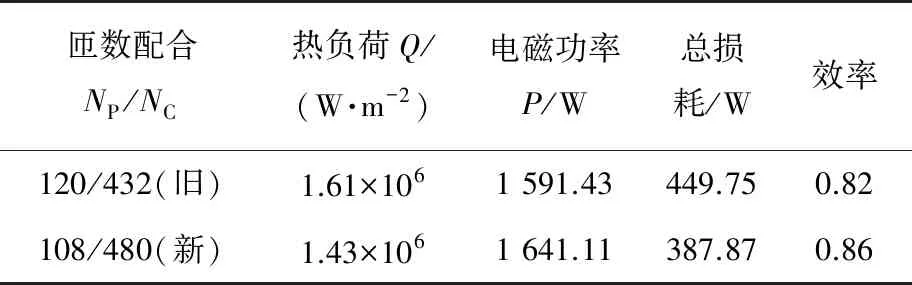
表5 Y280电机新旧匝数性能对比
2 其他模型验证
为验证该方法对BDFM定子绕组匝数配合优化的普遍适用性,另对其他文献[11-12]中的BDFM模型进行匝数优化及有限元仿真,电机模型基本参数如表6所示,有限元模型如图5所示。匝数筛选过程及仿真模型设置类比Y280 BDFM模型,此处不再赘述。对于D400 BDFM,选出功率绕组和控制绕组的新匝数配合为36/192,具体性能对比如表7所示。
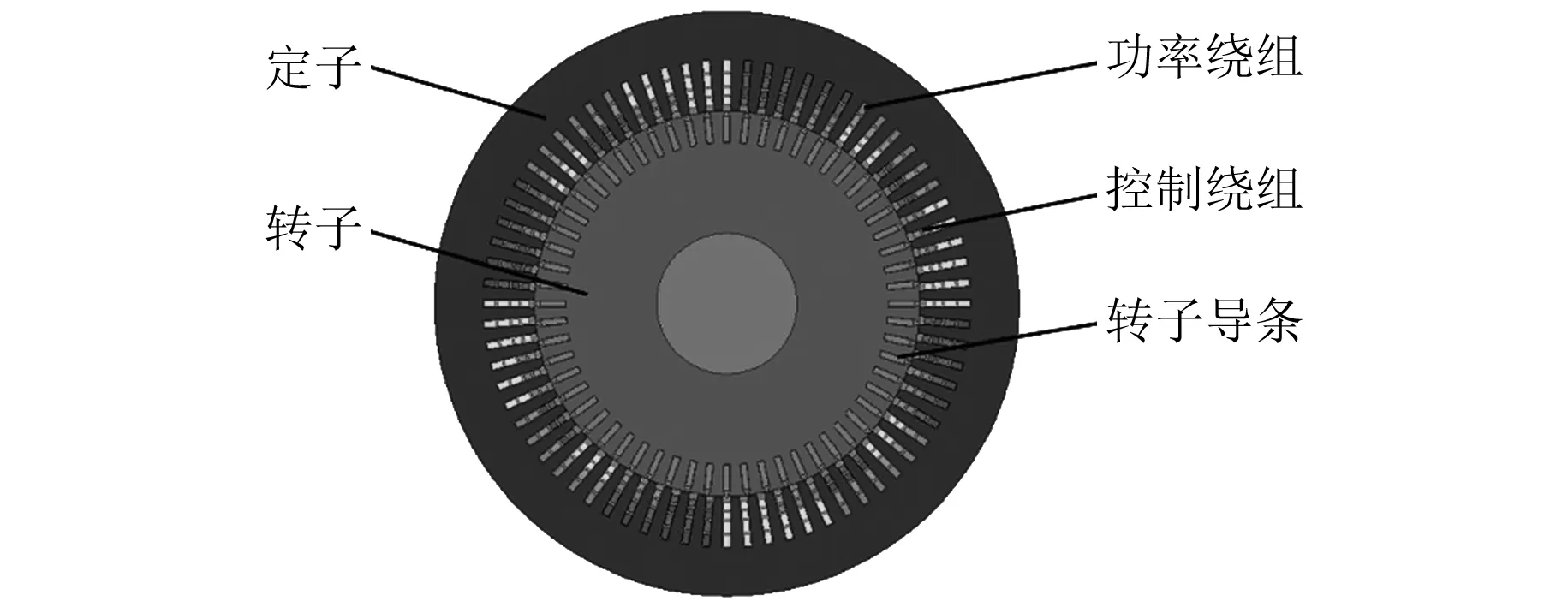
图5 D400 BDFM有限元模型

表6 D400 BDFM模型基本参数
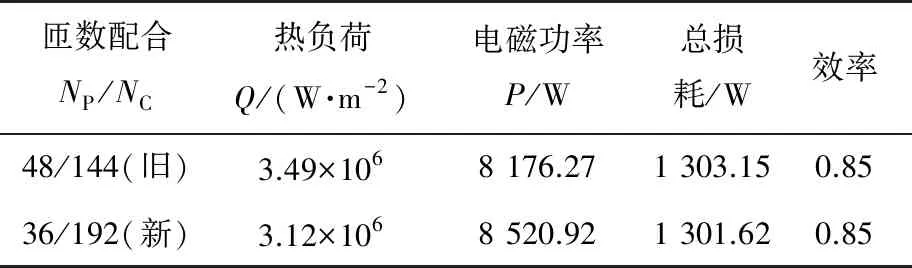
表7 D400 BDFM新旧匝数性能对比
3 匝数配合半解析优化流程图
本文所述的BDFM定子绕组匝数配合优化的流程如图6所示,具体可以分为以下四步。
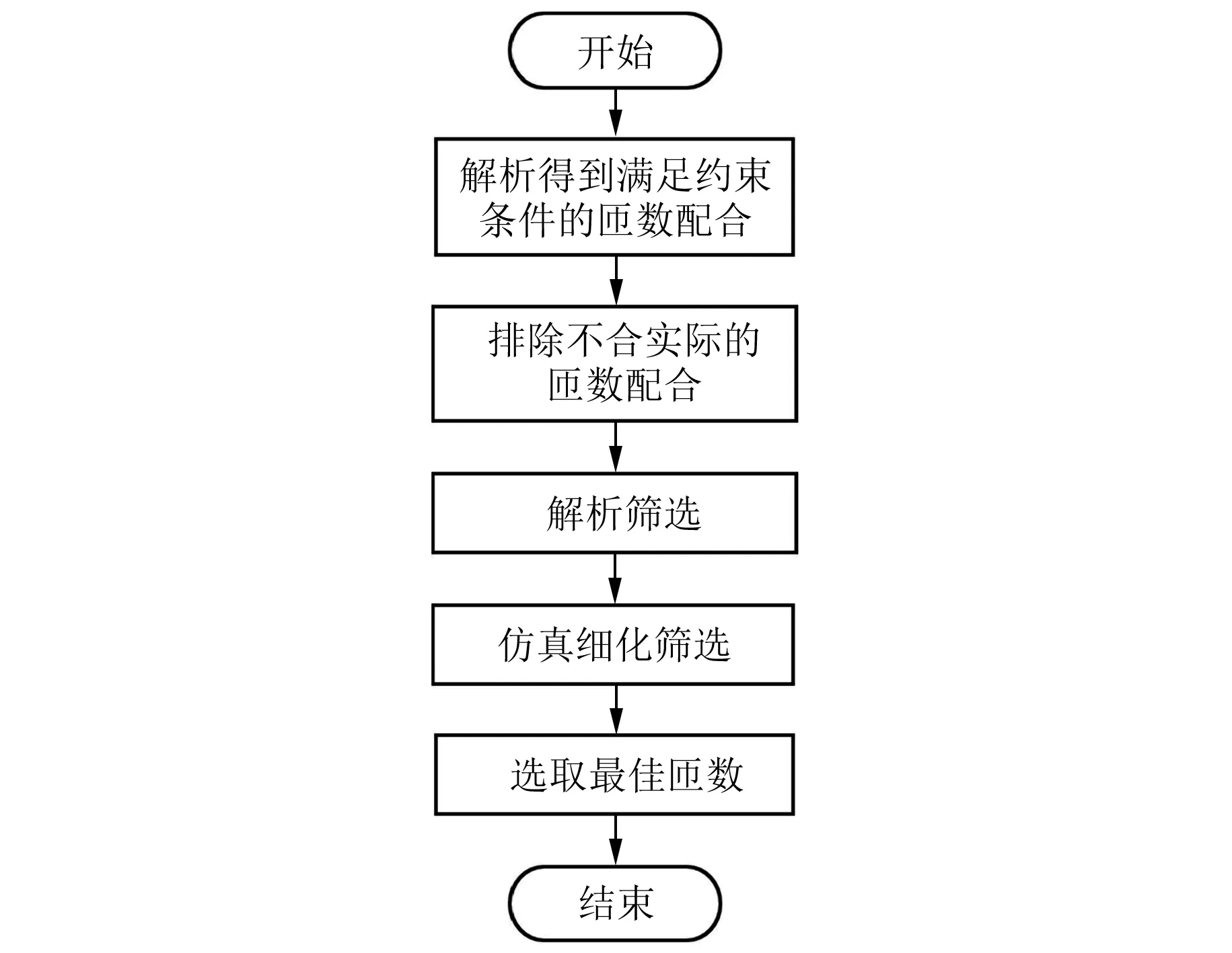
图6 匝数配合半解析优化流程图
第一步:以最大功率不变为约束条件,通过式(18)得到所有满足约束条件的匝数配合。
第二步:对满足约束条件的多组匝数配合进行初步理论排除筛选,使其满足1.3节的(1)(2)条件,且匝数配合结果应使电机在两绕组共同激励时能正常运行于双馈同步状态。
第三步:以电机热负荷最小为优化目标,为避免解析误差而导致漏失最优匝数配合,根据解析结果初步选出热负荷前3组或前5组较小的匝数配合。
第四步:对筛选出的匝数配合进一步仿真,最终对比选出其中热负荷仿真结果最小的一组,则该组匝数即为所有满足功率约束条件中热负荷最小的一组匝数配合。
4 结 语
本文提出了一种解析与仿真相结合的BDFM定子绕组匝数配合的半解析优化方法,以最大电磁功率不变为约束条件,以热负荷最小为优化目标,对定子两套绕组每相串联匝数进行筛选和分析,最终针对Y280 BDFM室模型选出一组满足功率约束条件且热负荷最小的匝数配合:Np=108,Nc=480,并在其他BDFM模型上进行优化,验证该方法对BDFM定子匝数优化的可行性与普遍适用性。本方法与完全依靠有限元仿真的匝数优化方法相比,显著减少了仿真次数,缩短了优化设计周期并节约了大量的计算资源。
