重复测量设计的单独效应分析

南方医科大学公共卫生与热带医学学院生物统计学系(510515) 谭旭辉 陈平雁

重复测量设计的单独效应分析

南方医科大学公共卫生与热带医学学院生物统计学系(510515) 谭旭辉 陈平雁△

目的探讨重复测量设计资料单独效应的分析方法。方法 分析单独效应的两种方法分别为基于一般的配对t检验和基于局部调整标准误的配对t检验方法，后者使用SPSS软件中一般线性模型下EMMEANS子句实现。用模拟方法分别比较两种方法的整体I型错误率。结果 使用两种不同标准误，统计分析结果存在较大差异。模拟结果显示，使用EMMEANS子句的整体I型错误率较一般的配对t检验方法有明显的降低。结论 基于局部调整标准误的EMMEANS子句分析单独效应更为合理。

重复测量 交互作用 单独效应 一般线性模型

△通讯作者：陈平雁

重复测量数据(repeated measures data)是指每个实验单位至少接受3次及3次以上的不同处理，或接受相同处理后，至少在3个及3个以上不同时间点进行测量，并获得相应次数的记录数据〔1〕。重复测量设计中，将因素分为组间因素和组内因素，并进行组间效应、组内效应以及两者之间交互效应的分析。通常情况下，如果重复测量设计的各因素之间有交互作用时，除分析主效应外，还应当进一步的分析各因素的单独效应。分析单独效应的方法有两种，一种是对重复测量因素进行一般的配对t检验，目前较为常用;另一种是基于局部调整标准误的配对t检验。两种方法究竟哪一种更为合理，本文将对其进行比较，以期为将来的应用提供依据。

方法与原理

1.分析模型

重复测量方差分析模型如下：

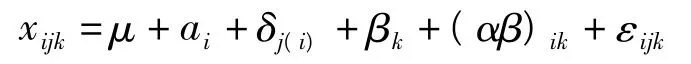
式中，xijk表示第i组中的第j个体在第k个重复观测点所得观察值;μ表示总体均数;ai表示组间因素A在i水平对应变量的附加效应;δj(i)是第i水平的第j个体的效应;βk表示组内因素B在第k个时间点对应变量的附加效应，(αβ)ik为 A和 B两者的交互效应，εijk为个体内随机误差项。

2.构造检验统计量

重复测量资料方差变异的分解见表1。

3.M矩阵与EMMEANS语句

SPSS的一般线性模型(GLM)过程使用最小二乘法对参数进行估计。使用GLM过程对重复测量资料进行分析，首先是对组内因素原始变量进行M矩阵转换，而对组间因素的转换，则产生变量Average，我们通常对组间因素所做的主效应分析就是依赖于该变量。例如，如果组间变量为Y1，Y2，Y3，其 M 矩阵为(/3/3/3)T，即每个元素均为变量个数平方根的倒数，则Average变量为：(Y1Y2Y3)(/3在GLM的默认选项下，也会对原始重复测量变量产生一组经正交多项式变换的变量，其个数为原始重复次数减去1，例如在原始重复测量变量个数为3的前提下，其产生Linear和Quadratic两个变量。

表1 重复测量资料的方差变异分解

在SPSS的syntax中，GLM过程中的EMMEANS Subcommand命令可用于比较各因素的单独效应〔2〕，其语法结构如下：

第一句为固定B因素在各个水平下，使用LSD方法比较 A因素的单独效应，也可以通过使用 ADJ(Bonferroni)方法来使用Bonferroni校正;第二句含义为固定A因素在各个水平下，使用LSD方法比较B因素的单独效应。在这里需要指出的是，在SPSS的syntax中，MANOVA过程的MW ITHIN Subcommand也可以用于分析单独效应〔3〕。其语法结构如下：

第一句为固定A因素(假定A有2个水平)在各个水平下，比较B因素的单独效应;第二句为固定B因素(假定B有3水平)在各个水平下，比较A因素的单独效应。

实例分析

为比较人乳腺癌细胞(MCF-7)及其经基因修饰后的细胞(T MCF-7)的活性，用MTT法进行测定，观测指标为细胞中线粒体内琥珀酸脱氢酶的活性，用光密度值(即OD值)来反映，OD值越大，说明细胞增殖活性越强，其数据如表 2〔4〕。

表2 两种细胞OD值的测定

此例为1个重复因素X(OD值)和1个独立因素A(细胞类别)的两因素设计，每个标本在五个不同的时间下进行测定。因此，我们进行Repeated Measures ANOVA，通过SPSS的重复测量分析我们可以看到，其 Mauchly’s Test结果为W=0.001，P=0.067。方差分析结果见表3。

表3 Tests of Within-Subjects Effects方差分析结果

由表3见组间因素与组内因素有交互作用，故需进一步分析各因素的单独效应。在SPSS的GLM过程中，我们通过设定EMMEANS语句来进行单独效应的比较，其编程语句如下：

将固定X在time1水平下，A因素的单独效应分析结果如表4;将A固定在1水平下，X的单独效应分析结果首先给出总的多元方差结果(表5)，并在此基础上进行两两比较(表6)，余类推。

在SPSS中，MANOVA过程也可以进行重复测量单独效应分析，其结果与GLM过程相同。在MANOVA过程中指定单独效应的语句如下：

分析结果见表4～表6。

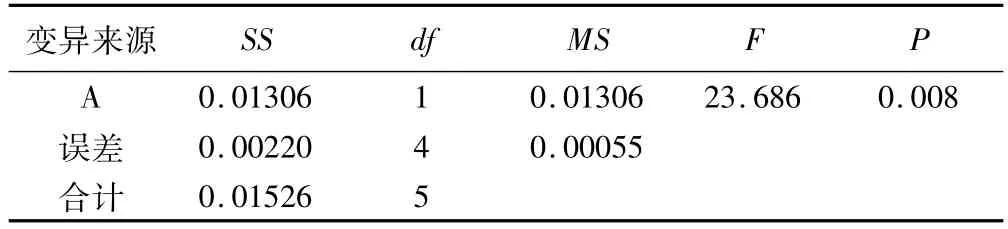
表4 在time1水平下A因素单独效应的方差分析结果

表5 多元方差分析结果

表6 在A为1水平下，X因素单独效应部分水平的两两比较

顺便指出，在SPSS当中，如果我们固定A因素为某一水平，比较X因素各水平之间的两两差别，即在RM ANOVA的OPTION选项里面选择X的LSD或者Bonferroni校正，其结果本质上等价于在A的各个水平下，对X的某两个水平做一般的配对t检验(一类错误为0.05)，而Bonferroni校正也是在配对t检验的基础上进行校正。而使用GLM过程的EMMEANS Subcommand，其使用的标准误是基于X某两个水平全部数据差值的Estimated Marginal Mean的标准误。而对于固定X因素的水平，比较A因素之间的两两差别，相当于固定X因素在某一个水平，对A因素各水平进行 One-way ANOVA 分析〔5〕。

为了解该语句对于控制总的第一类错误的效果，我们用SAS 9.1进行了初步模拟，设组间因素A为3水平，组内因素X为5个水平的重复，总体均数以及总体方差的设置见表7，A因素每个水平的样本量均为3，模拟次数为100次，产生的数据均满足球对称假定〔6〕。模拟结果显示，组内因素A固定在各水平下，在重复因素X所有水平之间的两两比较(共30次)中，使用 EMMEANS语句整体一类错误率比使用SPSS默认的LSD方法有较为明显的降低。

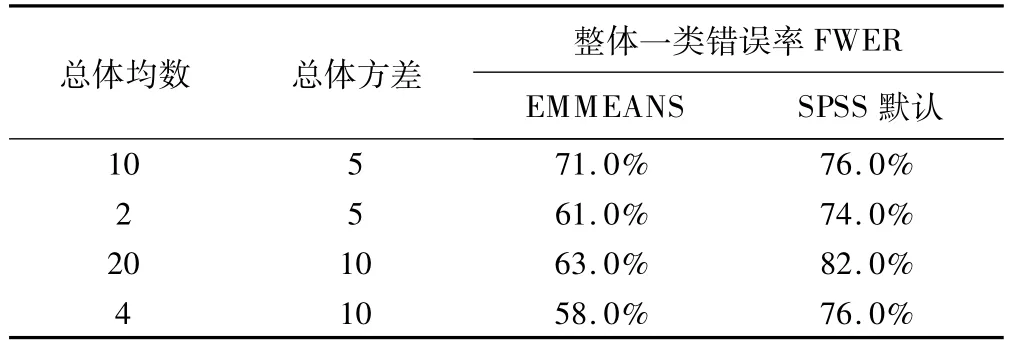
表7 两种方法的整体一类错误(FWER)的比较

讨 论

当重复测量设计因素间存在交互作用时，很有必要进行单独效应分析。在使用SPSS的GLM过程分析单独效应的一般应用中，若在OPTION选项里面所进行的重复因素单独效应的比较实际上就是配对t检验，通过上述模拟结果可见，其FWER要明显高于GLM过程的EMMEANS Subcommand处理方法，因此，对于满足球对称假定的数据，使用 EMMEANS Subcommand进行单独效应比较更为合理。

本文仅对重复测量设计资料分析单独效应的SPSS编程进行了简单介绍，并初步做了模拟验证，至于对不满足球对称假定的数据以及具有一定相关性的多元正态数据模拟研究，还有待后续的深入研究。

1.陈平雁.SPSS13.0统计软件应用教程.北京：人民卫生出版社，2005：160.

2.SPSS Inc.SPSS 13.0 Command syntax Reference.USA：SPSS Inc，2004：717-718.

3.Field AP.Discovering Statistics Using SPSS.London：SAGE Publication，2005：462.

4.胡良平.现代统计学与SAS应用.北京：军事医学科学出版社，2002：130.

5.Keselman HJ.Testing treatment effects in repeated measures designs：An update for psychophysiological researchers.Psychophysiology，1998，35：474-475.

6.Hugo Quené，Huub van den Bergh.Onmulti-level modeling of data from repeated measures designs：a tutorial.Speech Communication，2004，43：105.行的。球坐标变换对成分数据的利用有其独特的意义