存在热耗散时动态法测良导体热导率的研究

叶 军，徐 平，，陈子瑜，Ptrice Bottineu

（北京航空航天大学a．物理科学与核能工程学院；b．中法工程师学院，北京100191）

1 引 言

动态法测量良导体热导率时，一般采用单端周期加热法，通过检测热波从加热端到恒温端的传播速度，得到被测材料的热导率．目前大学物理实验中常用的动态测量方法中，为了避免因热耗散而引起的误差，普遍采用在良导体外侧包裹隔热材料，要获得高精度的实验结果，需要较为复杂的实验装置［1］，同时也忽略了高次谐波对实验结果的影响［2］．本文介绍的实验方法可以简化实验装置，同时有效地消除谐波引起的系统误差，提高了实验精度．

2 实验原理

一维半无限长的隔离均匀圆棒的热传导方程可以表述为［3］

式中u（x，t）表示圆棒的温度，D＝κ／cρ，c为圆棒的比热，ρ为其密度，κ为热导率．但由于在实际条件下，很难做到圆棒的热学隔离，因此必须考虑对流和辐射的影响，式（1）需要进行修正．

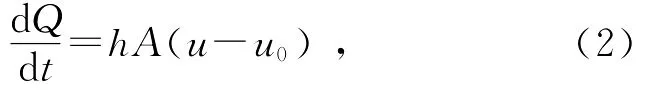
首先讨论对流的影响：热对流遵循牛顿冷却定律［4］，即式中u0为环境温度，u为热源温度，A为热源表面积，h是与传热方式等有关的常量，一般空气对流h为［5］2～25 W／（m2·K）．此处给出了单位时间内由于温度的差异而传播的热量．圆棒在d x长度内损失的热量为

式中P为圆棒的周长．此时方程（1）可以改写为［6－7］

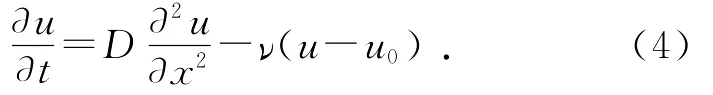
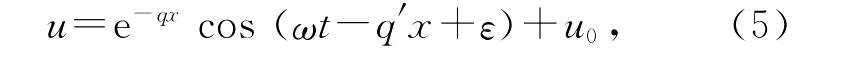
式（5）中q和q′是与ν和D 有关的常量，ε是热端温度变化简谐波的初始相位．

由于实验时采用周期性热源进行加热，因此可以将周期性热量分解为一系列傅里叶级数的叠加，温度变化为［6］

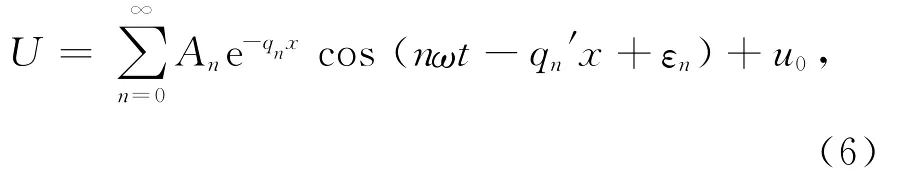
其中

式（6）中An与εn分别是周期性热源进行傅里叶展开以后，各个简谐波的幅度值和初始相位．式（7）与式（8）中同时取ν＝0，则可得不存在耗散时的计算公式［1］．

由式（6）可知，求出某一位置处温度的一个傅里叶级数的振幅或相位，与该傅里叶级数在另一位置的振幅或相位相比较即可求出热导率．

对于本实验所采集到的周期信号，由于数据是离散的，因此可以利用傅里叶变换来求得所需要的振幅谱和相位谱．

对于热辐射，满足［4］：

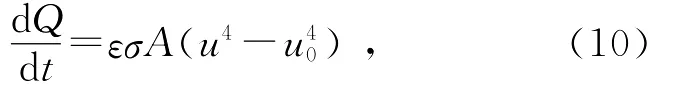
其中u为物体表面的热力学温度，u0为环境温度，玻尔兹曼常量σ＝5．67×10－8W／（m2·K4），ε描述实际物体与黑体发射热辐射能力的差别．由于热辐射在圆棒温度和环境温度差别不大时，其对实验的影响有限，此处予以忽略．在结果分析中将对热辐射强度做进一步讨论．

3 实验装置及测量方法

图1是实验装置的原理图．该装置由待测样品（铜棒）、热源和信号采集及处理部分组成．为了实现存在热耗散时的测量，其主要部件是1根长50 cm的裸露的待测铜棒，并布有热敏电阻阵列，用于采集铜棒的温度变化．因为热量沿着铜棒表面的耗散是微小量，可以假设热量在铜棒中是沿着轴向传播，在任意垂直于轴向的截面上的温度是近似相同的，因此只需确定铜棒轴线上各点温度的变化情况，就可以确定整个铜棒的温度变化情况．在铜棒长度足够长的条件下，可以认为铜棒的非加热端温度保持恒定，可以当作半无限长的系统来处理．

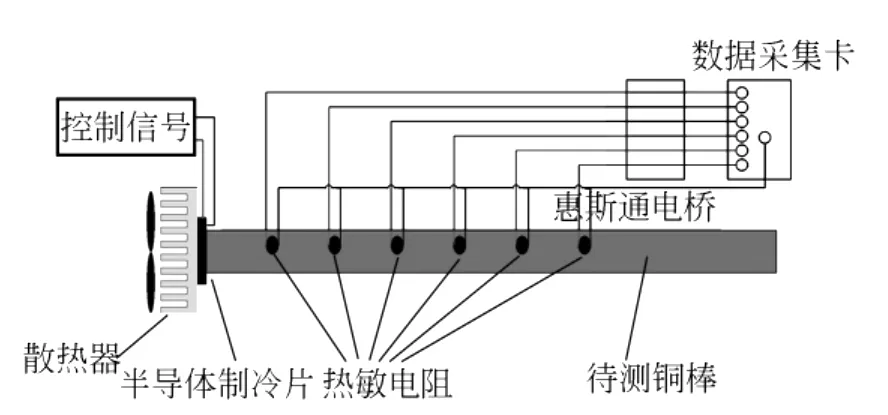
图1 实验装置原理图

测量是在各温度传感器具有稳定波形条件下进行的，因此首先需要对系统进行充分预热．再对实验采集到的数据采用快速傅里叶变换方法，以求出不同位置温度的振幅谱和相位谱．

4 结果分析

图2是实验过程中所采集到的各位置温度变化的情况．从图2中可观察到热波在传导过程中幅度不断地衰减，且谐波衰减速度比基波快，因此波形也在不断地变化，离热源越远处，谐波衰减得越多，波形更接近于正弦波．由此可以判断出在铜棒上离热源足够远的位置，谐波分量衰减殆尽，只剩下基波，可用传统的方法进行数据处理；但是由于谐波衰减至可以忽略的位置离热源比较远，这些位置的温度变化也非常小，因而对温度测量精度的影响会导致实验结果有很大的误差．

图2 铜棒各点温度变化曲线

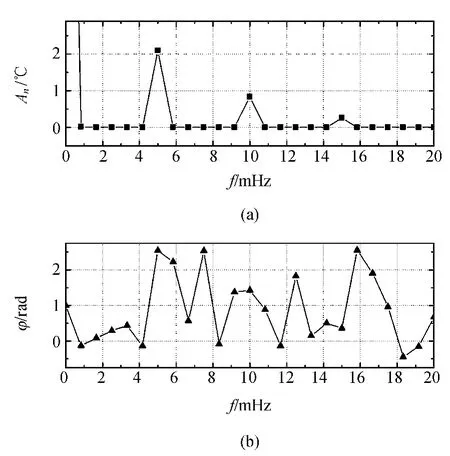
图3 第一个热敏电阻温度信号的幅度谱和相位谱

对温度变化曲线进行傅里叶变换，可以得到幅度和相位谱．第一个热敏电阻的幅度谱和相位谱如图3所示，可以清晰观察到热波的各个谐波，因此可以利用各个谐波的温度变化情况，对热导率进行研究，并且实验精度不会因为环境温度缓慢改变而改变，降低了对整个实验条件的要求，可以大大简化实验装置．

表1分别列出了6个热敏电阻在频率为5，10，15 m Hz处的振幅和相位．利用表1中各个热敏电阻热波在5 m Hz时的谐波得到的振幅变化曲线和不存在耗散时的理论值相比较，可得图4．从图4中可以看到实测曲线略低于理论曲线，说明热波在传播过程中其热量会沿着铜棒表面不断流失，并且会导致实际测量得到的热导率变小，同理分析相位亦可得相似的结论，因此引进式（9）的计算方法，可明显减少由于热损耗而引起的误差．

表1 测得铜棒各点在不同频率谐波下热波振幅和相位值

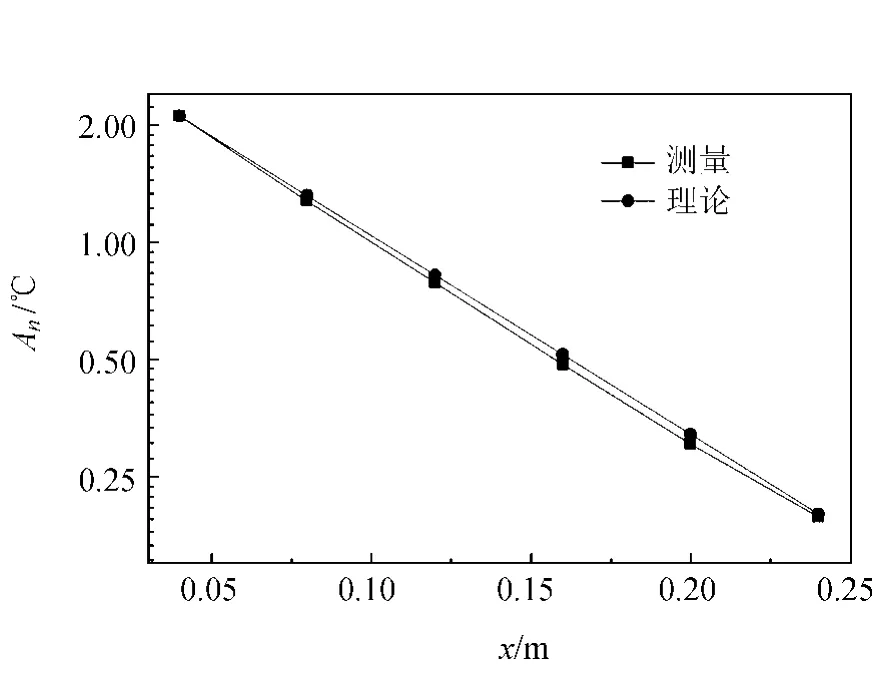
图4 各热敏电阻热波在5 m Hz谐波处振幅的实测值和理论值

由式（6）和式（9）可以看出，利用表1中的数据可以求得qn与qn′，从而计算出D，计算结果如表2所示，¯D＝0．000 115 1 m2／s，从而计算出热导率κ＝394 W／（m·K）．纯铜在20℃时，热导率κ的理论值为391 W／（m·K）［8］，则相对偏差η＝0．9%．

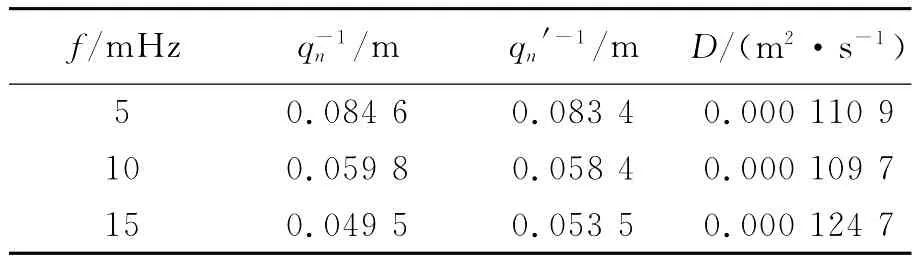
表2 铜棒各点在不同频率谐波下qn，qn′与D值

讨论辐射的影响．从表1可知，第一个热敏电阻在平衡位置的温度变化小于3℃，实验所用圆棒材质为紫铜，其高度抛光的发射率为0．03～0．04［5］，以环境温度为25 ℃，温度变化3 ℃，发射率0．04为例，利用式（10）可以计算出：

而对流的影响也可以由式（2）计算得到，取h＝2，则有：

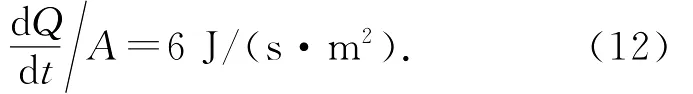
由式（9）可知，本实验中仅存在热对流时，不影响实验结果，而单独比较式（7）和式（8）中的参量ν可知，热对流对本实验结果的影响极其微小，在一定精度范围内可以忽略不计，且由式（11）和式（12）的结果可知，热辐射的影响仅是热对流的1／8，因此热辐射的影响也可以忽略．

5 结束语

由上述分析可知，该实验方法可以有效地提高存在热耗散时的测量精度，其原理清晰，计算方便，并且可以加深对热波传导过程的认识，同时由于方法本身的特性，简化了整套实验装置的结构，并且测得的实验结果具有较高的精度，适合在大学物理实验中应用．

［1］ 周慧君，江洪建，胡立群，等．热波理论的应用——良导热体热导率的动态法测量［J］．大学物理，2005，24（6）：47－49．

［2］ 杨帆，吕庶白，于瑶，等．热波法测良导体热导率实验中高频热波影响的分析与消除［J］．大学物理，2006，25（7）：50－52．

［3］ Sullivan M C，Thompson B G，Williamson A P．An experiment on the dynamics of thermal diffusion［J］．Am．J．Phys．，2008，76（7）：637－642．

［4］ 秦允豪．普通物理学教程·热学［M］．北京：高等教育出版社，2004：124，128．

［5］ 赵镇南．传热学［M］．北京：高等教育出版社，2002：13，507．

［6］ Carslaw H S，Jaeger J C．Conduction of heat in solids［M］．2nd edition．Oxford：Oxford University Press，1969：137－140．

［7］ Talpe J H，Bekeris V I，Acha C E．Measurement of thermal conductivity and heat capacity in an undergraduate physics laboratory ［J］．Am．J．Phys．，1990，58（4）：379－381．

［8］ 黄伯云，李成功，石力开，等．中国材料工程大典（第4卷）·有色金属材料工程（上）［M］．北京：化学工业出版社，2005：219．