L型构件双圆棒榫节点抗弯强度模型及其数值模拟

沈 杨，王天龙

(北京林业大学 木质材料科学与应用教育部重点实验室，木材科学与工程北京市重点实验室，北京 100083)

木质家具接合形式一般有榫接合、钉接合、胶接合、木螺钉接合以及连接件接合[1]。榫接合因精巧的外观、牢固的结构，从古代一直沿用至今。而家具的结构强度取决于其节点强度。对榫接合家具进行力学性能评估时，根据其连接方式，通常测定节点抗弯强度、抗拔强度或抗扭转强度，在同样连接方式下，抗弯强度往往小于抗拔强度及抗扭强度，故在进行榫接合家具结构设计时，需要重点考虑抗弯强度[2-4]。

在榫接合形式中，按照榫头形状可分为：直角榫、燕尾榫、圆棒榫、椭圆榫等，圆棒榫因节约木材、结构简单等优点，被广泛运用于传统木结构家具和现代板式家具中。为了探究圆棒榫在家具中的使用性能，有学者从纯理论的角度分析了圆棒榫在实木家具结构中的强度，论证其利用合理性并给出了使用相关注意事项[5]；也有学者针对T型、L型梓木构件，研究了圆棒榫各参数对接合性能的影响，给出了较优圆棒榫参数[6]；还有学者采用单因素试验法，得出了圆棒榫用于中密度纤维板接合时，各参数与接合强度的关系公式[7]。然而在现有圆棒榫接合强度相关研究中，大部分都是通过试验测试，得出仅适用于特定材料下的关系公式或结论[8-11]。这种研究方法往往受到材料差异、加工精度等不可控因素的影响，如要得到准确的结果则需要大量的重复试验，费时费力，故需要寻找一种具有普遍性的、能规避外部因素的研究方法。

目前有限元方法已经被广泛运用于板式家具的结构设计中，而对于榫接合家具的有限元方法运用研究相对有限，仍需进一步研究[12]。本研究采用有限元分析法，对双圆棒榫节点抗弯强度进行了研究，建立了可用于预测双圆棒榫节点抗弯强度的有限元模型，同时，进行抗弯强度试验，并将试验中材料相关参数带入模型，得到仿真值，并通过两者的比较对模型进行验证。

1 材料与方法

1.1 试验材料

试验基材采用梓木(Sassafrastzumu)，含水率平均值为10.4%，试件尺寸为150 mm×50 mm×25 mm。

双圆棒榫材料为桦木(Betulaalnoides)，圆榫类型为螺纹型，直径选用Φ6、Φ8、Φ10 mm，长度为40 mm。

1.2 试验方法

选取L型构件，圆棒榫与榫孔的配合为过盈配合，过盈量为0.1 mm，其结构示意见图1，参考GB/T 10357.3-2013《家具力学性能试验 第3部分：椅凳类强度和耐久性》[13]，设计图2所示的加载试验，在距节点100 mm处的部位进行加载，通过位移法进行加载，加载速度为10 mm·min-1，当位移量到达30 mm时，停止加载。

图1 试件尺寸及加载示意Fig.1 Schematic diagram of specimen assembly and loading

2 结果与分析

2.1 有限元模型建立

使用有限元仿真软件进行数值模拟，根据试验试件分别建立相应的有限元模型。

1)根据图1的装配图分别建立L型试件、加载头以及圆棒榫的几何模型，并根据真实情况装配。

2)赋予材料属性，将木材设定为正交各项异性材料，并考虑到木材的塑形。构件赋予梓木的材料属性，9个弹性参数[14]见表1，并根据实际情况指派材料方向；圆棒榫弹性模量为10 000 MPa，泊松比设定为0.27[15-16]；加载头设定为刚性材料。

表1 基材材料的9个弹性参数Table 1 Nine elastic parameters of the base material

3)创建相互作用属性，分析实际加载情况，确定仅双圆棒榫与榫孔之间有摩擦，其余部件为刚性连接。因此创建接触属性，设定切向方向接触类型为摩擦，摩擦系数为0.54，法向方向为“硬”接触。创建圆棒榫表面与榫孔内表面的接触关系，并设定过盈配合，过盈量为0.1 mm。

4)创建载荷和边界条件，设定L型构件里竖直构件底部X、Y、Z3方向的铰接固定。因为本研究加载方式为位移加载，故设定加载最大位移为30 mm，考虑到实际情况，并保证计算结果的收敛性，需要添加预紧力，设定初始位移为0.01 mm。

5)划分网格，根据有限元理论，网格的划分决定着计算的准确度，网格越精细，单元越多，计算结果越准确，但计算量也会急剧增大。综合考虑结果准确度和网格均匀性，设定网格大小为5 mm，类型为四面体，划分技术为自由，所用算法为默认算法，并在边界合适地方使用映射的三角形网格。

6)优化与作业提交，检查模型网格，对于榫孔处部分畸变网格进行优化，并检查整体模型，确定无模型干涉后，提交作业进行计算。

2.2 有限元过程分析

图2为有限元分析结果，其中图2(a)为L型试件在加载完成后的变形情况；图2(b)为双圆棒榫在加载过程中的应力变化过程；图2(c)为双圆棒榫加载过程中各部位等效塑形应变过程。

由图2(a)可知，在位移达到30 mm时，双圆棒榫接合的L型构件已失去连接强度，双圆棒榫并未出现断裂现象；由图2(b)可知，在加载过程中，初期加载时，双圆棒榫所受的最大应力是榫1顶部中间所受的拉应力，然后随着位移量的增加，最大应力为榫1底部中间所受的压应力，接下来为榫2顶部的拉应力、榫2底部的压应力。当双圆棒榫应力达到最大值时，榫1和榫2的顶部及底部中间都受到较大应力，随着位移量进一步增加，榫1顶部拉应力骤减，榫1和榫2底部压应力持续增大。由此可以得知是因为榫1顶部达到了屈服应力而使圆棒榫最大应力减小；同时，由图2(c)可知，随着加载过程的进行，试件最大等效塑性形变由榫2到榫1，最终出现在榫2顶部中间，而榫1顶部中间没有塑性变形，这是因为在有限元分析中，如果单元所受应力超过了屈服应力，会被删除。实际试验中，在榫1和榫2上表面都观察到了开裂现象。这说明有限元分析结果与试验结果基本吻合，材料变形情况与试验中的榫头变形情况一致。

图2 有限元分析结果Fig.2 Finite element analysis results

2.3 抗弯强度仿真验证

通过双圆棒榫节点能承受的最大载荷来表示抗弯强度，故通过软件后处理模块，输出有限元模型中加载头节点处的支反力—位移曲线(图3)，由图3可知，不同直径下的支反力均呈现先线性增加，然后呈对数增加，最终趋于固定值，其变化趋势与实际加载试验中的载荷位移曲线一致。由图4可知，在不同直径下，有限元分析结果与试验结果之间的误差也不相同。在直径为6 mm时，有限元分析的极限破坏载荷为524 N，与试验结果的最大误差为18.32%，最小误差为3.05%，平均误差为12.79%；直径为8 mm时，极限破坏载荷为805 N，与试验结果的最大误差为11.57%，最小误差为2.99%，平均误差为6.92%；直径为10 mm时，曲线上最大载荷为1 102 N，但考虑到分析误差，取值为1 030 N，与试验结果的最大误差为17.18%，最小误差为2.23%，平均误差为8.43%。综上可得，有限元分析结果与试验结果的平均误差均<15%，在工程允许范围内，可以用于实木榫接合家具的设计[17-18]。

表2 模拟结果与试验对比Table 2 Comparison of simulation results and experiments

图3 抗弯强度对比Fig.3 Comparison of bending strength

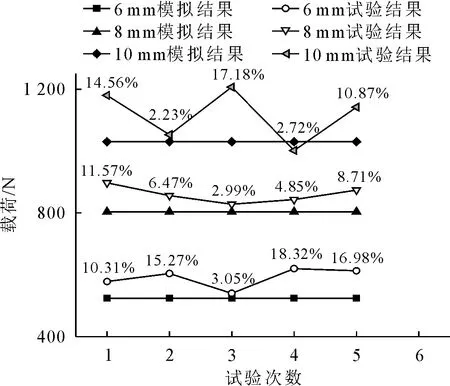
图4 误差分析Fig.4 Analysis of error

在有限元分析过程中，当使用几何非线性法进行求解计算时，在材料的强度方面，当某个单元达到屈服应力时，模型会删除该单元，从而降低材料刚度，而在实际中，木材在达到屈服强度后，木材的断裂为韧性断裂，不会影响材料的刚度，因此导致模拟值偏小；在模型的损伤方面，由于模型存在大位移和断裂的情况，会导致无法得到精确结果，在确保结果准确性的前提下，一般会设定合适大小的阻尼，从而得到精确结果，但在设置阻尼后，会在一定程度上减小所产生的应力和应变。同时，由于木材是一种非均质、各向异性的材料，木材的力学性能又受到密度、含水率、缺陷等因素影响，试验测试时难以保证试件的完全一致，因此试验测试结果会在一个范围内波动。

2.4 直径对双圆棒榫抗弯强度的影响

对不同直径下双圆棒榫抗弯强度仿真值进行比较，结果见图5，在L型构件中，双圆棒榫抗弯强度随着直径的增加而增加。但圆棒榫直径从6 mm增大为8 mm时，平均抗弯强度从524 N增加到804 N，增加幅度为53.4%；直径从8 mm增加为10 mm时，平均抗弯强度从804 N增为1 030 N，增加幅度为28.1%。这表明随着圆棒榫直径的增加，增加幅度逐渐降低。这可能的原因是在抗弯强度试验中，圆棒榫节点处存在着剪切力、破坏弯矩以及轴向抗拔力，其中影响最为显著的是破坏弯矩。当破坏形式为圆棒榫屈服，圆棒榫直径越大，根据弯矩计算公式，可知其对应的破坏弯矩越大，故抗弯强度随直径呈递增关系。但在L型构件中，在圆棒榫直径增大的同时，榫孔离边的距离就越小，从而在试验中，也会发生构件自身损坏的现象，从而影响抗弯强度增加幅度。

图5 直径对抗弯强度的影响Fig.5 Effect of diameter on bending strength

3 结论

建立的模型能较好地仿真实际过程中节点的损伤形式和破坏强度，可以将此模型运用于榫接合家具结构设计，并预测圆棒榫接合的抗弯强度。

在L型双圆棒榫接合节点中，主要破坏形式为圆棒榫损伤，节点抗弯强度随着直径的增加而增大，但其增幅逐渐减小，仿真值与试验值的误差均<15%。

直径为10 mm和8 mm的双圆棒榫结构强度均达到国标规定的承重结构强度要求，可用于椅子后腿与望板、腿与扶手连接处；但直径为6 mm的双圆棒榫不适用于家具承重连接处。