汽车轮毂多道次旋压成形工艺分析及数值模拟

钱陈豪，贾建磊，李 萍，薛克敏

（合肥工业大学材料科学与工程学院，安徽合肥，230009）

金属旋压工艺是将被加工的金属坯料套在芯模上，而坯料则通过尾顶压在芯模的端部，并与芯模一起随着主轴旋转，而旋轮沿着芯模移动。在旋轮的压力下，利用金属的可塑性，逐点将金属加工成所需要的空心回转体制件。按照旋压时坯料壁厚的变化，旋压工艺可分为普通旋压和剪切旋压两种。前者在加工前后壁厚基本保持不变，而后者则会发生壁厚的减薄[1－3]。将旋压工艺应用于轮毂成形，既能保证轮毂有足够的刚度，又能大大减少坯料的厚度，使其比传统铸造轮毂更轻便耐用。由于旋压成形技术的复杂性，单纯采用试验或理论解析方法难以准确、高效地解决生产中的实际问题，而采用数值模拟技术则能弥补上述不足。有关旋压成形技术目前已开展一些工作，朱利民[4]介绍了轮毂旋压工艺的优点及其生产原理；张小光等[5]讨论了等强度车轮旋压对工艺和设备的要求，但对轮毂多道次旋压过程的数值模拟尚未有相关报道。为此，本文以A356铝合金轮毂多道次旋压成形为研究对象，运用Abaqus软件建立了轮毂多道次旋压有限元模型，并分析了轮毂各道次下减薄率、进给比、旋轮圆角半径等工艺参数对旋压力的影响。

1 成形工艺

图1为汽车铝合金轮毂的锻坯和零件。由于轮毂锻坯几何形状复杂，轮辋为不规则的复杂曲母线，单一道次旋压成形很难得到既符合形状尺寸又满足性能要求的零件，所以需采用剪切旋压与普通旋压的复合成形工艺。以剪切旋压为主要成形手段完成轮辋壁厚的减薄并达到轮辋性能要求后，再用普通旋压修整轮辋局部难以成形的区域，直至满足旋压成形要求。另外，考虑到材料最大减薄率受到限制，至少需要采用两个道次的剪切旋压完成总的壁厚减薄，所以旋压成形方案拟定为先进行两道次剪切旋压，再进行普通旋压，每道次后都要进行退火处理，以消除残余应力。

图1 汽车铝合金轮毂锻坯和零件Fig.1 Aluminium alloy hub and its pre－formed blank

选择合适的工艺参数是保证坯料顺利进行旋压成形的条件，在旋压过程中，主要的工艺参数有减薄率、旋轮圆角半径、进给比和芯模转速等[5－10]。减薄率是影响剪切旋压成形主要的工艺因素，在确定减薄率时要考虑材料的强化要求及其成形极限。异形件旋压时所采用的旋轮圆角半径一般为毛坯厚度的1～2倍。进给比取值一般为0.3～2.5 mm／r，常用的进给比为0.5～1.5 mm／r[1]。旋压时的芯模转速对坯料旋压成形的影响不大，可以在0.5～5 r／min内选取。模拟中拟定的具体参数如表1所示。

表1 旋压成形各道次模拟参数Table 1 Process parameters of multi－step spinning

2 有限元模型

坯料成形方案确定后，利用Abaqus CAE模块的三维造型功能建立各道次下旋压的有限元模型。为简化模型以提高运算的精度和速度，只对轮毂锻坯变形部分进行模拟分析。定义坯料为刚塑性变形体，所用材料为A356铝合金，弹性模量为70 MPa，泊松比为0.5，屈服强度为133 MPa，并采用八节点实体单元类型（C3D8R）划分其网格；定义芯模和旋轮为解析刚体，无需对其划分网格。芯模与一对旋轮绕着各自对称轴旋转，旋轮同时沿自身轴线的轴向进给；而毛坯底部与芯模底部通过绑定约束，使得毛坯跟随芯模一起旋转。旋压过程中涉及到的旋轮与坯料、芯模与坯料之间的接触区均采用罚函数摩擦模型。建立的旋压有限元模型如图2所示。

图2 旋压有限元模型Fig.2 Finite element models of spinning

3 模拟结果与分析

3.1 应力分析

图3 第1道次旋压成形过程中毛坯等效应力分布Fig.3 Distribution of equivalent stress during the first pass

图3为第1道次剪切旋压的毛坯应力分布云图。由图3可看出，旋压过程中坯料的应力集中区域随着成形时间的推进先增大后减小。这是因为在旋压成形的初期，已变形区域要小于未变形区域，旋压已变形区受到未变形区凸缘“刚端”的影响要大，正弦律偏离程度较大，产生了附加的径向拉应力和周向压应力，以致造成应力极大值的分布区域较大；在旋压成形的后期，已变形的区域比未变形的区域要大，所受到凸缘“刚端”影响就相对较小，正弦律偏离程度小，从而使应力极大值的分布区域也较小。偏离率对工件尺寸精度和材料可旋性都有影响，但实际生产中要做到完全不偏离正弦律是很困难的，零偏离仅是理想剪切变形的设想。本次模拟中分两次减薄，这样单次减薄量较小，能将偏离率控制在合理的范围内。

轮毂的第2道次成形与第1道次同属锥形件的剪切旋压过程，经过第2道次旋压后的坯料应力和应变分布与第1道次类似。与第1道次不同的是：第2道次应力极大值的分布区域要小一些，这是因为第2道次的变形程度小于第1道次的变形程度，并且第2道次内锥角增大幅度小于第1道次相应值，其正弦律偏离程度也相对较小，所以受到的“刚端”影响要小。第3道次普通旋压成形是轮毂外形的主要成形阶段，这个阶段坯料发生类似的较大弯曲变形，旋轮轴向力是坯料成形的作用力。图4为第3道次旋压成形终了时等效应力的轴向分布。由图4可看出，在坯料轴向距离为18 mm和90 mm附近区域等效应力出现较大起伏，这正是对应轮毂的两处弯曲区域，旋轮经过这两处区域时受到的轴向阻力较大。而在40～80 mm区域等效应力值在120 MPa上下波动，因为此区域为极小锥角锥形件，近似于筒形件，旋轮轴向力作用不明显，所以在实际加工中，旋轮进给至弯曲区域时应当留意将进给比调小，以降低轴向力。

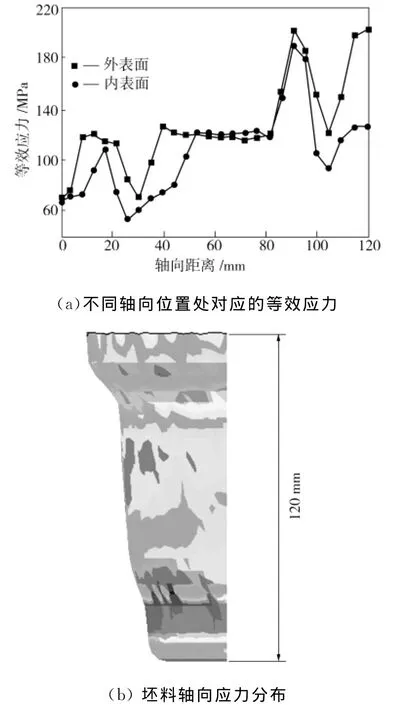
图4 第3道次旋压成形终了时等效应力轴向分布Fig.4 Axial distribution of equivalent stress after the third pass

3.2 应变分析

图5为第1道次剪切旋压的毛坯外表面等效塑性应变分布云图。在坯料的变形过程中，外表面的等效应变经历了一个先增大后减小的过程，使得在坯料中间部位出现一个应变极大值集中区的“应变环”，并且应变分布比较均匀。第2、3道次内外表面也会出现一个“应变环”。产生“应变环”的原因有两种：一是在旋压成形中期，由于受到未变形区凸缘“刚端”的影响，坯料的内锥角会相对增大，依据正弦定律，就会使旋压件壁厚的减薄率增大；在旋压成形后期，受到未变形区凸缘的影响较小，以致内锥角恢复到原来大小，使实际旋压件壁厚的减薄率也相应减小；二是尽管金属基本上向旋轮后方流动，但仍有少量的金属流向旋轮的前方，造成旋轮前方坯料的凸起。随着坯料变形的进行，凸起的金属会被旋轮压下，同样会造成实际旋压件壁厚减薄率的增加，等效应变也会相应增大。当坯料的变形终了时，坯料的变形恢复到正常状态，金属的堆积减小，等效应变相应减小。旋压过程中的凸起是旋压成形金属流动的正常现象，如果金属的凸起过大，会造成金属凸起高度、实际减薄率和旋压力的增加，使金属的流动处于不稳定状态，严重时会造成起皮等旋压缺陷，所以要严格控制金属的凸起现象。通过调整合理的工艺参数，将金属的凸起严格控制在合理的范围内，就可以保证旋压过程能够正常进行。

图5 第1道次旋压成形过程中毛坯等效塑性应变分布Fig.5 Distribution of equivalent plastic strain during the first pass

图6为各道次旋压成形终了时的等效应变轴向分布。由图6可看出，第1道次等效应变最大，第3道次等效应变最小。这是因为第1道次减薄率最大，而第3道次普通旋压毛坯不发生减薄。普通旋压时具有不改变厚度层的特点，也使其毛坯内外表面等效应变差距不明显（见图6（c））。相反地，第1、2道次剪切旋压结束后，毛坯外表面等效应变要明显大于内表面相应值（见图6（a）、图6（b）），表明内外侧金属流动情形不同，其原因是剪切旋压时正弦律的偏离所致。

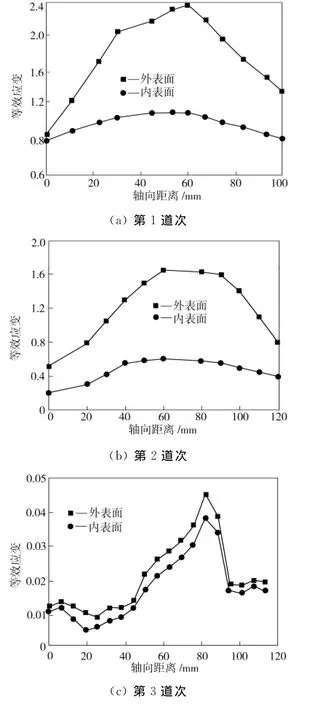
图6 各道次旋压成形终了时等效应变的轴向分布Fig.6 Axial distribution of equivalent strain after each pass

3.3 工艺因素对旋压力的影响

强旋旋压力的计算对于选择旋压机、设计工装、确定工艺参数和了解剪切旋压过程都具有重要意义。剪切旋压变形力的大小主要取决于旋压的单位塑流压力和旋轮对工件的加压面积，凡是对两者有影响的因素都将对旋压力产生影响。

图7为工艺因素对旋压力的影响。旋轮圆角半径和进给比等参数保持恒定，第1道次减薄率分别取值为20%、25%、30%、35%，对应的第2道次减薄率依次取值为37.5%、33.3%、28.5%、23%。减薄率与旋压力之间的关系曲线如图7（a）所示。由图7（a）可看出，无论是第1道次还是第2道次，旋压力总是随着减薄率的增加而增大。减薄率对旋压力影响最大，这是因为减薄率增加即意味着旋轮与工件接触面积增大，也就是变形量增加，因而变形力必然会明显提高。

减薄率和进给比等保持恒定条件下，第1道次的旋轮圆角半径分别取值为16、18、20、22 mm，第2道次的旋轮圆角半径分别取9、11、13、15 mm。旋轮圆角半径与旋压力之间的关系曲线如图7（b）所示。由图7（b）可看出，随着旋轮圆角半径的增大，旋压力也逐渐增大，这是因为加大旋轮圆角半径，使旋轮与坯料之间的接触面积增大，旋轮下变形金属的体积也相应增大，因此造成旋压力的值相应增大。总之，适当地减小旋轮圆角半径值，对降低变形力有利。

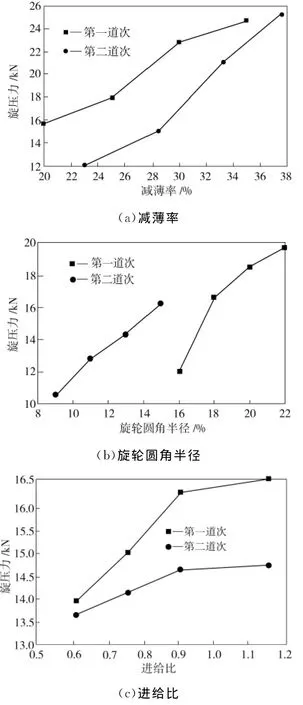
图7 工艺因素对旋压力的影响Fig.7 Influence of main process factors on spinning force

减薄率和旋轮圆角半径等保持恒定条件下，进给比分别选取0.6、0.75、0.9、1.05 mm／r，第1道次与第2道次进给比选取相同。进给比与旋压力之间的关系曲线如图7（c）所示。由图7（c）可看出，旋压力随着进给比的增加而增大，且开始时其增速较快，当进给比达到0.9 mm／r时，其增速开始减缓，这是因为在旋轮进给过程中，它与工件接触处变形面积的轨迹是一个螺旋带。当进给比较小时，后一转的螺旋带与前一转的螺旋带有一部分重合，而重合部分在前一转中已经变形，故所需的力较小。随着进给比的增大，重合部分减小，因而变形力增大。当进给比增大至螺旋带不再重合时，变形力增加减缓。总之，进给比的影响力虽不如减薄率大，但也是影响旋压力的主要因素之一。

4 结论

（1）在剪切旋压阶段，应力最大值始终出现在旋轮和坯料的接触区，并且应力极大值区域主要集中在坯料的外表面，随着变形程度的增加而增大，应变分布经历了一个先增大后减小的过程，在坯料的中间部位出现了一个应变环；在普通旋压阶段，应力的内外表面分布基本相似，应变极大值则集中在芯模圆角区等变形比较大的区域。

（2）减薄率是影响旋压工艺的主要因素。随着减薄率的增大，坯料前金属的凸起和旋压力迅速增大，但减薄率的最大值也受到旋压成形极限约束；旋压力随着进给比的增加而增大，且开始时其增速较快，当进给比达到0.9 mm／r时，其增速开始减缓，进给比的影响力虽不如减薄率大，但也是影响旋压力的主要因素之一；适当减小旋轮圆角半径值，对降低变形力有利。

[1] 日本塑性加工学会.旋压成形技术[M].陈敬之，译.北京：机械工业出版社，1988：30－72.

[2] Music O，Allwood J M，Kawai K.A review of the mechanics of metal spinning[J].Journal of Materials Processing Technology，2010，210（1）：3－23.

[3] Kathryn J，Julian A.The mechanics of incremental sheet forming[J].Journal of Materials Processing Technology，2009，209（3）：1 158－1 174.

[4] 朱利民.先进的铝轮毂设计与制造技术[J].铝加工，2008（2）：45－47

[5] 张小光，钟志平，张建荣，等.旋压技术在等强度钢制车轮制造中的应用[J].锻压技术，2009，34（2）：24－26.

[6] 詹梅，李虎，杨合，等.大型复杂薄壁壳体多道次旋压成形过程中的壁厚变化[J].塑性工程学报，2008，15（2）：115－120.

[7] 杨合，孙志超，詹梅，等.局部加载控制不均匀变形与精确塑性成形研究进展[J].塑性工程学报，2008，15（2）：6－14.

[8] 徐文臣，单德斌，吕炎，等.小锥角零件多道次剪旋成形试验研究[J].材料科学与工艺，2004，12（1）：33－36.

[9] 王强.普通旋压的弹塑性有限元分析及变形机理研究[D].哈尔滨：哈尔滨工业大学，1990.

[10] Quigley E，John M.The finite modeling of conventional spinning using multi－domain models[J].Journal of Materials Processing Technology，2002，124（3）：360－365.