液压缸稳定性设计的模糊可靠性计算

龚相超，胡百鸣

（武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北武汉，430065）

有关液压缸临界载荷的计算方法很多，但不同的计算方法和计算模型结果差别很大[1]，原因是液压缸所受载荷的工作阶段及环境因素的不同，致使液压缸的失稳因素具有某种不确定性，即模糊性和随机性。常规液压缸稳定性计算采用的是安全系数法，该法较大程度上依赖于设计者的经验，因而不能充分反映实际存在的诸多不确定性因素的影响，为此，本文采用模糊可靠性方法来计算液压缸的稳定性。

1 模糊可靠度计算原理

设液压缸工作压力P和临界压力Pcr分别为论域U，V上的模糊子集S、R，故P∈U，Pcr∈V，且用数s、r来表述，s∈[0，1]，r∈[0，1]，s、r分别为S、R的隶属度。S、R的隶属函数分别为fs（P）、fr（Pcr）。模糊子集R中每个元素Pcr都可以作为稳定性判据，因而将传统设计中的单一判据扩大为判据空间，在此基础上进行液压缸稳定性可靠度的计算，以此增大与实际情形相符的概率[2]。

设判据实空间Ω，对任意一个作为判据Pcr（Pcr∈Ω）都指定一个数μr∈[0，1]，即判据Pcr对模糊判据集（临界压力模糊子集R）的隶属度，考虑到设计的安全因素，其隶属度函数采用连续偏小型隶属度函数。液压缸的轴向压力P可按随机变量来设计，常见的分布有正态分布、威布尔分布等，一般根据实际工况来确定，本文计算采用正态分布。根据模糊等效随机原理，将复杂的模糊不确定性等效为随机不确定性[3]，得到工作压力概率密度分布函数与液压缸临界压力Pcr的隶属函数组合，液压缸稳定性模糊可靠度可采用概率密度函数联合积分法积分得到，也可采用功能密度函数积分法得到[4]。

2 临界压力隶属函数

表1 临界载荷计算值Pcr、实测值Pcr1及相对误差δTable 1 Theoretical and experimental critical load values

传统液压缸稳定性设计多采用欧拉公式和拉金公式[5]，且将液压缸视为理想的等截面直杆，截面惯性矩取活塞杆与缸筒中较小者。研究表明，该法所得临界压力值趋于保守，作为判据的可信度为1。采用文献[6]试验数据，临界载荷欧拉计算值、实测值及相对误差如表1所示。从表1中可以看出，所有临界载荷的实测值均较计算值大，最大相对误差为30.7%，最小相对误差为1.3%，平均相对误差为19.2%。因此临界载荷的隶属度函数采用降半阶正态分布[7]，如图1所示。临界压力为正态型模糊变量，其隶属度函数可表示为

式中：μr（Pcr）为模糊临界压力的隶属度函数；Pcr为模糊临界压力；ar为等截面欧拉公式计算值；σr为模糊临界压力的标准差。

图1 临界载荷隶属度函数Fig.1 Membership grade function of critical load

σr是反映液压缸真实临界压力合理取值的重要参数，将液压缸临界压力这一模糊变量等效为随机变量，则模糊临界压力等效概率密度函数为

3 模糊可靠度

鉴于现场工况较为复杂，液压缸所受荷载具有很大的随机性，故将本文液压缸随机载荷视为正态分布形式，其概率密度函数为

式中：P为随机载荷；as为随机载荷均值；σs为随机载荷标准差。

为了使计算结果尽可能符合实际情况，随机载荷标准差σs应根据实际统计数据确定。基于现场诸多不确定性因素，as的离散性很大，故取

对于已知临界压力和工作载荷概率密度的情形，可采用概率密度函数联合积分法得到可靠度[4]，概率密度函数联合积分原理如图2所示。代入载荷和临界压力的概率密度函数积分后可得液压缸稳定性可靠度R。

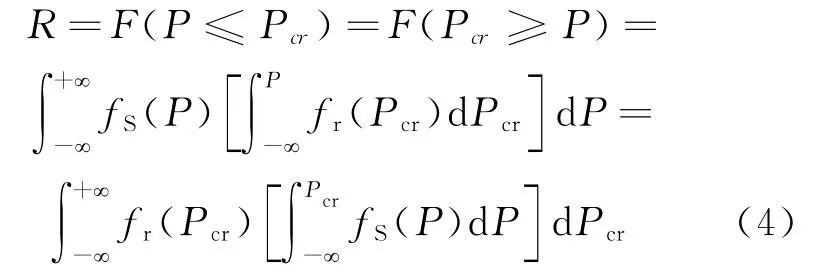
若式（4）积分得不到原函数，则可用数值积分计算出可靠度。由于本文液压缸的临界压力和工作载荷均为正态分布，且二者为相互独立的随机变量，所以采用功能密度函数积分法[3]得到。定义随机变量Z＝Pcr－P仍服从正态分布N（aZ，σZ），其中；可靠性指数则可靠度符合标准正态分布。

图2 概率密度函数联合积分Fig.2 Joint probability density function integral

液压缸可靠度可查标准正态概率积分表得到。可见用式（5）来计算稳定性可靠度简单易行。

4 计算实例

沿用文献[1]表2中的第5号液压缸，等截面直杆临界压力计算值和试验实测值分别为126.27 k N和153.46 k N，相对误差为17.7%，将数值代入式（1），且σr＝0.192ar，可得临界压力的隶属度函数和等效概率密度函数分别为

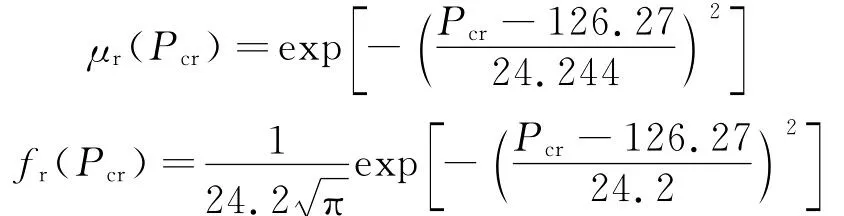
鉴于液压缸工况环境复杂，取安全系数为k＝2，as＝ar／k，且令σs＝0.2as

对于工况特别复杂的情形，可取k＝2.5，令σs＝0.3as，则β＝3.235 0，R＝0.999 4。考虑到液压缸的临界载荷受到液压油、导向长度、约束等诸多因素的影响，参考表1中数据，宜取σr＝0.2ar和σs＝0.2as。

5 结语

本液压缸稳定性可靠度计算方法为复杂环境和载荷及特殊工况下的设计提供了一条新思路，可以降低传统液压缸设计中对设计者经验的依赖性。本文中的几个重要参数的选取仅参考了表1中的1组实验数据，要想获得与实际情况吻合的理想参数值，尚需进行大量的试验数据统计分析。本文各个参数和概率的计算采用了MATLAB软件编程，MATLAB提供了丰富的概率统计函数，使得计算程序异常简洁。

[1] 龚相超，胡百鸣.基于能量原理的液压缸静力稳定性的计算[J].矿山机械，2011（3）：109－112.

[2] 郭书祥，吕震宙.概率模型含模糊分布参数时模糊失效概率计算方法[J].机械强度，2003，25（5）：527－529.

[3] 董玉革.机械模糊可靠性设计[M].北京：机械工业出版社，2000：16－19.

[4] 刘扬松，徐小兵.机械模糊可靠性理论与应用[M].武汉：中国地质大学出版社，2002：29－31，79－81.

[5] 王益群，高殿荣.液压工程师技术手册[M].北京：化学工业出版社，2010：159－160.

[6] 郭应龙.液压缸稳定性分析[J].武汉水力电力学院学报，1988（2）：23－29.

[7] 蒋泽军.模糊数学教程[M].北京：国防工业出版社，2004：27－30.

[8] 杨雄.井架实腹式轴心压杆稳定性计算新方法[J].石油机械，2006，34（8）：28－29.