基于ABAQUS的边坡失稳综合判据法

蔡路军，马建军，周大华，刘 松，潘 欣

（1.武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北武汉，430065；2.湖北省十堰至白河高速公路建设指挥部，湖北十堰，442000）

1 常用边坡失稳判据

采用强度折减有限元法分析边坡稳定性的一个关键问题是如何根据有限元计算结果来判别边坡是否达到极限破坏状态。目前常用的边坡失稳判据主要有：（1）有限元计算不收敛；（2）坡体或坡面位移突变；（3）潜在滑移面塑性区贯通。

采用第1种判据的理由是：有限元计算迭代过程就是寻找外力和内力达到平衡状态的过程，整个迭代过程直到一个合适的收敛标准得到满足才停止，如果边坡失稳破坏，滑面上将产生没有限制的塑性变形，有限元程序无法从有限元方程组中找到一个既能满足静力平衡又能满足应力－应变关系和强度准则的解，此时不管是从力的收敛标准，还是从位移的收敛标准来判断，有限元计算都不收敛。这样处理自然可以避开临近极限状态的计算，但采用有限元计算不收敛作为破坏标准包含一定的非确定性人为因素，并且在有些情况下计算结果可能会有较大误差，因为不收敛可由多种原因引起，比如荷载步长过大或体系内不同部分的刚度相差悬殊而使其数值性态较差。另外，有限元数值计算收敛时也不一定表明边坡处于安全状态[1－6]，因此将有限元计算的收敛性作为边坡的失稳判据不具备广泛的适用性。

采用第2种判据的理由是：由理想弹塑性材料构成的边坡进入极限状态时，必然是其一部分土体相对于另一部分发生无限制的滑移。尽管各种因素对位移和塑性应变等计算结果有较大影响，但这些因素不能改变边坡濒临破坏时位移突变的本质趋势，因此建议采用特征点处的位移突变作为边坡处于极限状态的判据，这样可以减小非确定性因素对安全系数的影响，但是该方法中特征点的选取对安全系数计算结果的影响较大[7]。

第3种是以边坡的等效塑性应变区从坡脚到坡顶贯通作为边坡发生整体失稳破坏的判据[8－10]。这种方法物理意义明确，但也有其不精确之处，因为在进入极限状态前，土工结构的塑性区也可能是贯通的，并且区域还可能较大。例如在计算一水平土层的自重应力时，如果土层的泊松比偏小，则开始计算时由于土体内剪应力水平较高，整个土体均处于塑性区。但通过弹塑性计算，土体内水平应力增大，而体系保持稳定并不破坏。所以，由计算显示的塑性区贯通来认定极限状态也是一种近似处理。另外，文献[4]认为，边坡破坏的特征是广义剪应变从坡脚到坡顶上下贯通，其物理意义较明确，但广义剪应变不仅含有塑性分量，而且也包括弹性分量，虽然广义剪应变的大小能够在一定程度上反映土体的剪切破坏状态，但是并不能准确地描述土体塑性区的发生与发展过程。因此，根据广义剪应变来判断塑性区及剪切破坏区的发展，并以此作为判断失稳的指标还是不够合理和准确。

上述3种判据都有其局限性，因此在采用强度折减有限元法计算边坡稳定安全系数时，笔者认为宜联合采用特征点处的位移突变和塑性区是否贯通等作为边坡失稳的判据，并且在用特征点位移突变作为判据时，应尽量在坡顶和坡趾处的特征部位设立多个观察点，以考察其位移与塑性区随强度折减系数的变化规律。

2 综合判据法

强度折减有限元法和极限平衡法实质上都是基于塑性力学理论的极限分析方法，因此这两种方法的分析过程和计算结果应该具有一致性，故一般采用小应变分析，此时数值不收敛判据是可行的。但边坡在失稳过程中，可能产生大应变问题，这时就不能用数值不收敛作为判据了，否则会导致结果偏大。为了使数值计算在边坡破坏后能收敛，应采用大应变分析，并建立位移突变判据。

塑性区贯通是边坡破坏的必要条件，但不是充分条件，考虑到塑性区贯通的客观指标很难确定，目前只能通过人的主观判断，从而不可避免地增加不确定性人为因素，因此在实际应用过程中，塑性应变区贯通的判据可作为前两种判据的补充。

综上所述，综合判据法步骤如下：

（1）进行小变形有限元计算，以计算不收敛为边坡失稳判据。对给定的抗剪强度参数折减，进行小变形有限元计算，直至计算不收敛，得出安全系数F1。

（2）进行大变形有限元计算，以位移突变为判据。以边坡上某几点为监测点分析其位移与折减系数的关系，拟合曲线，得出安全系数F2。

（3）在上述两种方法中，观察塑性应变区贯通状况，如出现异常再进行讨论。通过综合分析比较，得出合理的安全系数F。

在进行有限元计算时，应用的软件是ABAQUS。ABAQUS是一套功能强大的工程模拟有限元软件，其解决问题的范围从相对简单的线性分析到许多复杂的非线性问题。ABAQUS是目前处理岩土工程问题时应用较广的计算软件，其涵盖丰富的材料模型库，可以较为准确地模拟岩土这种特殊材料，在解决岩土力学中复杂的非线性问题方面优势显著。

3 标准算例

本文选择澳大利亚计算机应用协会（ACADS）的一道考核题作为标准算例，利用强度折减有限元法来比较采用各种失稳判据获得的边坡稳定性系数，并与采用不同条分法计算得到的结果以及参考答案进行比较，综合分析各种判据的适用条件。该算例为一均质边坡，坡高H＝10 m，坡角β＝26.6°，土体密度ρ＝2 t／m3。为了与传统的极限平衡法计算结果进行比较，土体计算采用理想弹塑性本构模型、莫尔－库仑屈服准则和相关联流动法则，黏聚力c＝32 k Pa，内摩擦角φ＝10°，膨胀角ψ＝φ，弹性模量E＝10 MPa，泊松比μ＝0.25。

均质边坡的有限元分析模型和网格划分如图1和图2所示。网格划分为1 012个单元、1 084个节点。边坡分析模型的左右边界均采用水平约束，底面采用水平竖向约束。

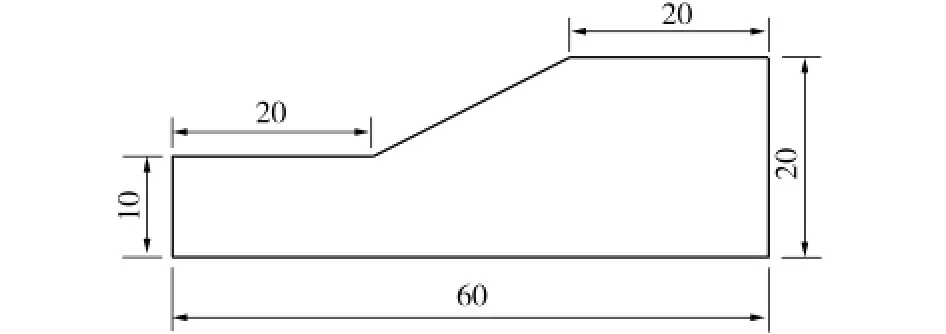
图1 边坡分析模型Fig.1 Model of the slope

图2 边坡有限元网格划分Fig.2 FEM mesh of the slope

3.1 小变形计算

应用小变形计算方法，要求精度达到0.001，通过计算，最后确定安全系数为1.698。应用小变形计算方法时边坡塑性应变如图3所示。此时，位于顶端的39＃节点A、中部的43＃节点B、底部的47＃节点C的位移如表1所示，其中U1、U2和U分别为节点的水平位移、垂直位移和总位移。

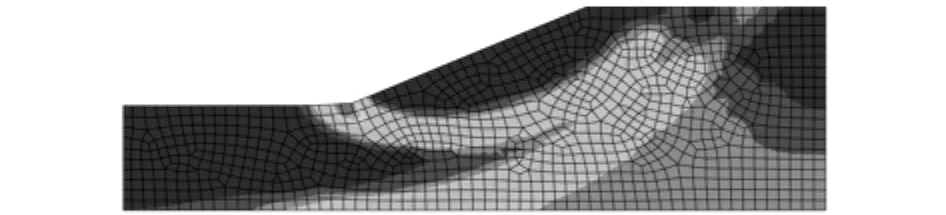
图3 边坡等效塑性应变图Fig.3 Equivalent plastic strain distribution of the slope

3.2 大变形计算

应用大变形计算方法，得出A、B、C点的位移如表2所示。

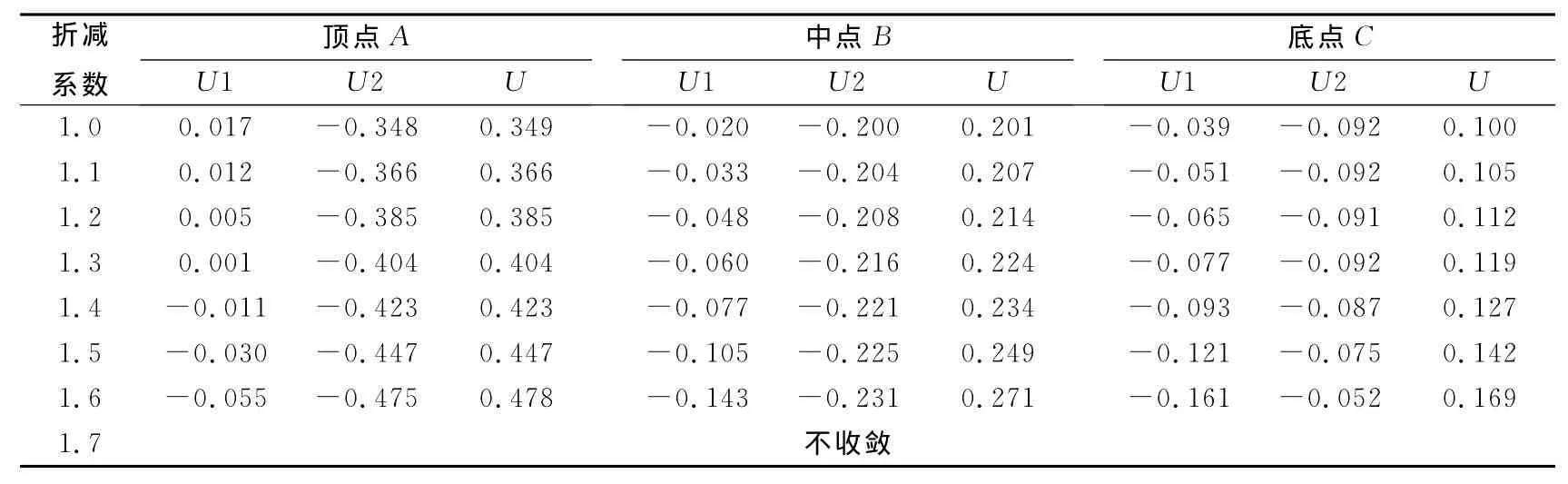
表1 小变形计算位移量Table 1 Displacement of small deformation calculation

表2 大变形计算位移量Table 2 Displacement of large deformation calculation

A、B、C点的水平位移与折减系数的关系如图4所示。从图4中可以看出，当折减系数达到1.70后，各点水平位移明显出现较大的增量，因此可近似认为安全系数为1.70～1.80。从3条曲线的切线拟合情况来看，可进一步将安全系数定为1.70。

图4 节点水平位移与折减系数的关系Fig.4 Relationship between horizontal displacement and reduction factor

在不同的折减系数K下，A、B、C点的水平位移发展过程如图5所示。从边坡的塑性应变（见图3）和水平位移的发展过程可以看出，边坡失稳过程大致可分为3个阶段：（1）稳定发展阶段。重力载荷开始施加时，潜在滑移面周围的土体单元产生塑性应变，但坡体位移变化不大。（2）滑移带初步形成，位移增大阶段。随着载荷增加，坡体位移增大，塑性应变也增大，土体塑性区沿着滑动面向上爬升，直至坡体内的滑移带初步形成。（3）位移突变，坡体失稳阶段。如果载荷继续增大，则坡体位移急剧增大，边坡沿滑移带发生整体失稳，塑性应变贯通。

3.3 结果分析

以有限元计算不收敛为边坡失稳判据，对边坡稳定进行小变形有限元计算，得出安全系数为1.698，强度折减有限元法搜索到的潜在滑动面与传统的极限平衡法得到的结果一致；再以位移突变为边坡失稳判据，进行大变形有限元计算，得出安全系数为1.70。综合分析小变形和大变形计算条件下的边坡安全系数，再结合塑性区贯通情况，可确定其安全系数为1.70。

对于此例，采用极限平衡法中的简化Bishop法计算得出的安全系数为1.687，ACADS对该算例给出的边坡安全系数参考值为1.65～1.70。本文得出的结果与ACADS给出的参考值较为接近，与简化Bishop法的结果相差仅0.76%，这证明了本文方法的可行性与准确性。

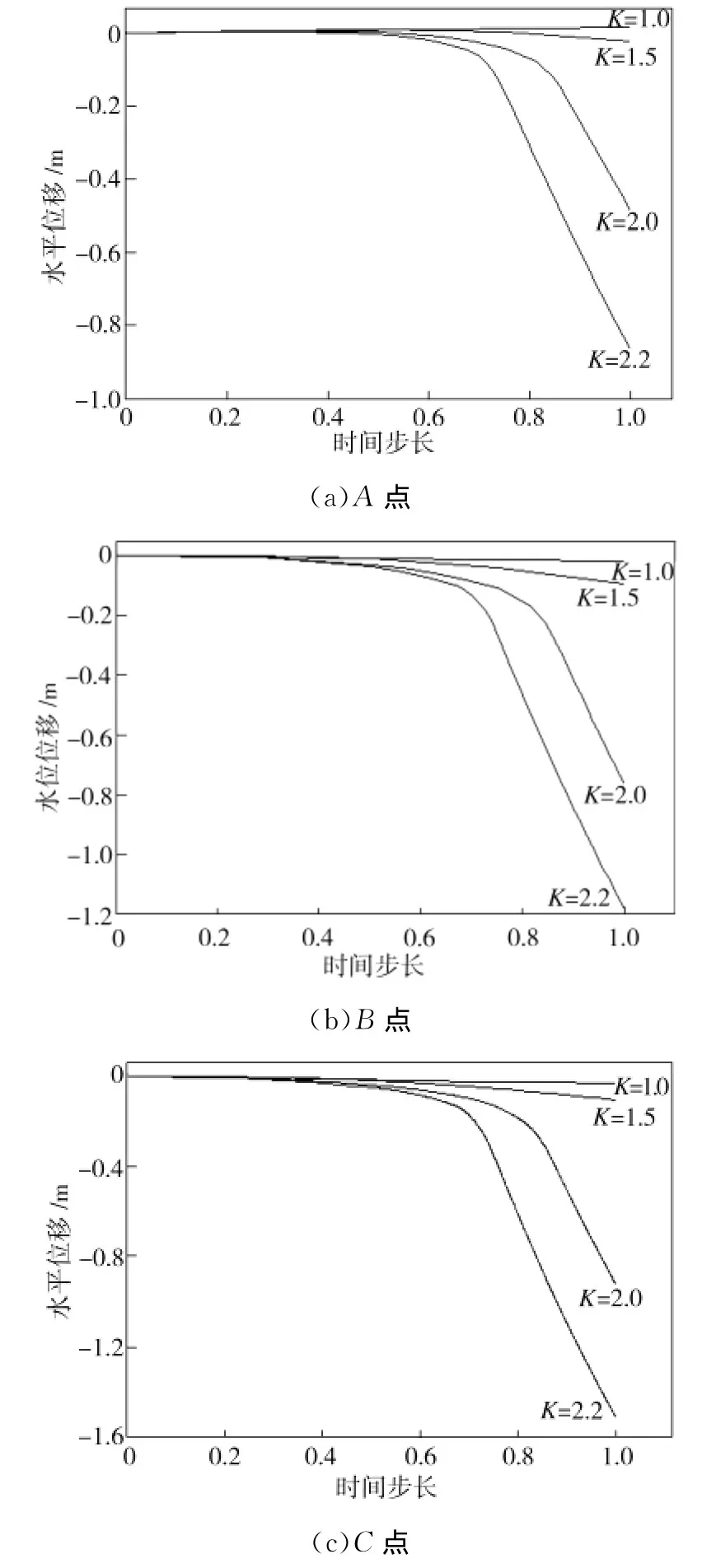
图5 节点水平位移与时间步长的关系Fig.5 Relationship between horizontal displacement and time step

4 工程实例

某一基坑开挖深度为3.0 m，采用1∶1放坡开挖。参照文献[3]对计算区的研究结论，计算范围取为总宽度18 m，深度10 m，具体尺寸如图6所示。土层分为3层：第1层为杂填土，ρ＝1.8 t／m3，E＝5 MPa，c＝15 k Pa，μ＝0.3，φ＝23°，厚度为1.0 m；第2层为淤泥质粉质黏土，ρ＝1.9 t／m3，E＝3 MPa，c＝5 kPa，μ＝0.45，φ＝16°，厚度为3.0 m；第3层为粉土与粉砂互层，ρ＝1.78 t／m3，E＝10 MPa，c＝10 k Pa，μ＝0.45，φ＝16°，厚度为6.0 m。约束条件：右侧和左侧坡底下为水平向约束，底面为水平和竖向双向约束的铰接约束。

采用本文提出的方法，以计算不收敛为边坡失稳判据，对边坡稳定进行小变形有限元计算，得出安全系数为1.278，分别采用强度折减有限元法和传统极限平衡法搜索到的潜在滑动面具有一致的结果；再以位移突变判据，进行大变形有限元计算，得出安全系数为1.30。综合分析小变形和大变形计算条件下的边坡安全系数，并结合塑性区贯通情况，可确定其安全系数为1.30。采用极限平衡法中的简化Bishop法对此例计算得出的安全系数为1.276，二者很接近，再次证明了综合判据法的合理可行。

图6 开挖边坡示意图Fig.6 Schematic diagram of the foundation slope

5 结语

在采用强度折减有限元法进行边坡稳定性分析的过程中，采用综合判据法对边坡是否达到极限状态进行判定，不会出现以偏概全的极端情况，可更准确地计算边坡安全系数，所得结果与采用传统极限平衡法得到的计算结果吻合良好。但综合判据法的缺点是计算较为复杂，其中在大变形计算时以位移突变作为判据存在人为因素，难以精准控制。

[1] Griffiths D V，Lane P A.Slope stability analysis by finite elements[J].Geotechnique，1999，49（3）：387－403.

[2] Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Geotechnique，1999，49（6）：835－840.

[3] 张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报，2003，34（1）：21－27.

[4] 赵尚毅，郑颖人，张玉芳.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学，2005，26（2）：332－336.

[5] 刘金龙，栾茂田，赵少飞，等.关于强度折减有限元方法中边坡失稳判据的讨论[J].岩土力学，2005，26（8）：1 345－1 348.

[6] 佀赟，皇甫军.有限元强度折减理论求安全系数及存在的问题[J].西部探矿工程，2007，19（2）：203－206.

[7] 宋二祥，高翔，邱玥.基坑土钉支护安全系数的强度参数折减有限元方法[J].岩土工程学报，2005，27（3）：258－263.

[8] 连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边破的稳定性[J].岩土工程学报，2001，23（4）：406－411.

[9] 栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报，2003，23（3）：1－8.

[10] 郑宏，李春光，李焯芬，等.求解安全系数的有限元法[J].岩土工程学报，2002，24（5）：625－628.