矩形的弦长分布
2011-01-23李德宜杨佩佩
李德宜,杨佩佩,李 亭
(武汉科技大学理学院,湖北武汉,430065)
1 基本方法
设D为平面凸体,即具有非空内部的紧凸集。G=G(p,φ)为平面中的直线,其广义法式方程[1]为xcosφ+ysinφ=p,称(p,φ)为直线G的广义法式坐标。用λi(E)表示点集E的i维测度。σ表示直线G被凸体D截出的弦长,σ=λ1[G(p,φ)∩intD],当G仅与边界∂D相交时(含G∩∂D是线段的情形),约定σ=0。
定义1 设D为平面凸体,对任意给定的σ及φ(0≤φ<2π),称二元函数
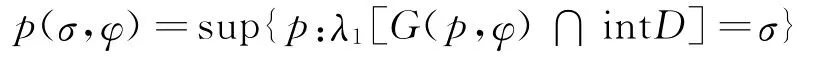
为凸域D的广义支持函数[1-2]。
定义2 以σM(φ)表示垂直于φ方向的直线G被凸体D截出的弦长最大值,即

对任意给定的l(≥0)及φ(0≤φ<2π),令

称二元函数r(l,φ)为凸域D的限弦函数[1-2]。
定理1[3]设K为周长等于L的凸体,G为随机直线,则有

2 凸体弦长分布函数的定义
设K为周长等于L的平面凸体,有关K的一些随机变量、平均量得到了广泛关注和研究,比如K内两点间的平均距离[4]、平均弦长[5]等。设G为随机直线,当G与K相交时,G被K截得的弦长σ也是随机的,本文讨论弦长的分布。
定义3 设K为平面凸体,G为与K相交的随机直线,截出的弦长为σ,弦长分布函数[3]F()y定义为
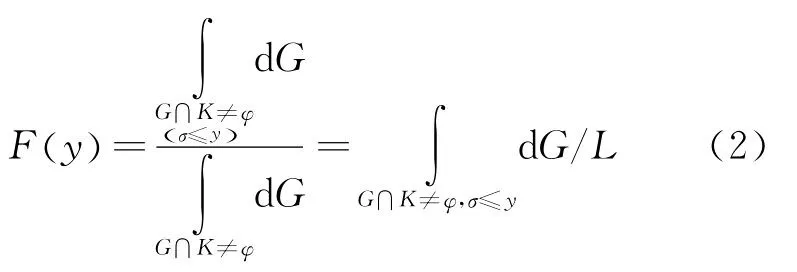
3 矩形的弦长分布函数
对于光滑严格凸的凸体,较容易求出弦长分布函数,但当凸域具有平行边时,因为弦长定义中的特殊约定,对它的处理则需要单独进行。
定理2 边长为a和bb≤()a的矩形的弦长分布函数F(y)为

证明:在平面上取直角坐标系xoy,设矩形域为(R),不失一般性,可设b≤a,矩形的直径记为d,由对称性,可以仅考虑的情形。此时,矩形的最大弦长函数为
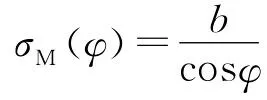
矩形域(R)的限弦函数r(l,φ)为

矩形的广义支持函数为

求矩形的弦长分布主要是求出积分

等式右边第3项是由于平行边而必须添加的,即
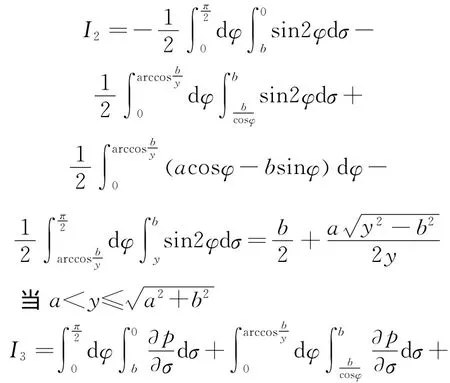

等式右边第3项和第7项是由于平行边而必须添加的,即
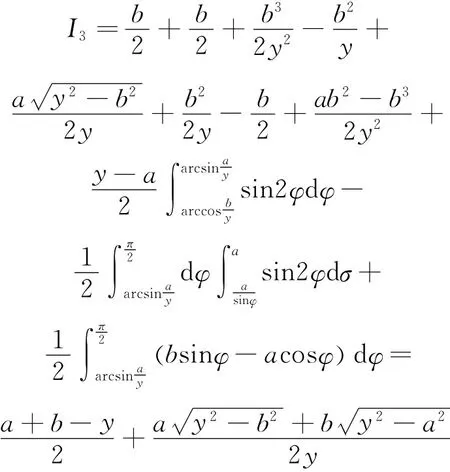
根据矩形的对称性

证毕。
推论 边长为a的正方形的弦长分布函数为
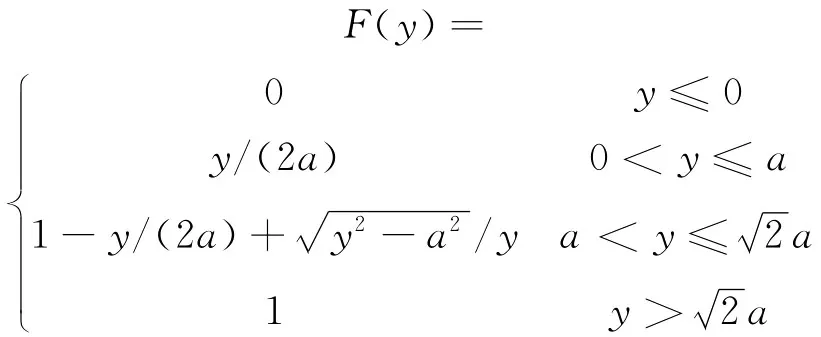
[1] 任德麟.积分几何学引论[M].上海:上海科学技术出版社,1988:3-5,71-73.
[2] Ren Delin.Topics in integral geometry[M].Singapore:World Scientific,1994:70-78.
[3] L A Santalo.积分几何与几何概率[M].吴大任,译.天津:南开大学出版社,1991:40-89.
[4] 程鹏,李寿贵,许金华.凸域内两点间的平均距离[J].数学杂志,2008,28(1):57-60.
[5] 赵静,李德宜,王现美.凸域内弦的平均长度[J].数学杂志,2007,27(3):291-294.
