飞向晕轨道的探测器轨道优化

2010-12-11胡少春孙承启刘一武

空间控制技术与应用 2010年4期

关键词：燃耗流形射入

胡少春，孙承启，刘一武

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

飞向晕轨道的探测器轨道优化

胡少春1，2，孙承启1，2，刘一武1，2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

晕轨道的稳定流形为从地球到晕轨道的转移轨道设计提供了便利.以往都采用在晕轨道上的目标点施加脉冲，这样，稳定流形只是为转移轨道的设计提供一个初始猜想，探测器并没有运行在稳定流形上，因而并未真正利用稳定流形节省燃料的优势.利用基于序优化理论的微分修正法，研究从晕轨道近地点稳定流形上不同点进入稳定流形所需要的燃料消耗，寻找燃耗最少的转移轨道.仿真表明，对于晕轨道近地点入轨，找到的稳定流形射入点机动比以往的晕轨道入轨点机动节省约33%的燃料消耗.此外，还对晕轨道上不同入轨点的入轨代价进行了研究，得到了晕轨道近地点入轨的最小燃耗解.

平动点；星际高速公路；晕轨道；稳定流形；序优化；微分修正

圆型限制性三体问题中存在5个(动态)平衡点，称为平动点或拉格朗日点.这5个点L1～L5都位于两个大天体的运动平面内，其中L1、L2和L3位于两个大天体的连线上，称为共线平动点.星际高速公路(IPS，interplanetary superhighway)是由太阳系内所有围绕共线平动点的不稳定周期轨道和拟周期轨道的不变流形组成的轨线网络，探测器可以无动力地沿着IPS到达或者远离平动点附近的周期轨道和拟周期轨道.因此，利用不变流形设计转移轨道可大大节省燃料消耗，这对于遥远的深空探测活动意义非凡.文献[1-3]正是基于IPS理论为Genesis探测器设计了采样返回轨道.

由于从地球上看去，围绕共线平动点的周期轨道像环绕在太阳或月球周围的一个“晕”，因此文献[4]中称其为晕轨道(或称Halo轨道).晕轨道的稳定流形为晕轨道目标点到地球停泊轨道的转移轨道设计提供了便利.对于小幅度晕轨道而言，与其相关的稳定流形距离地球很远，除了在地球停泊轨道附近施加一次机动，还需要在晕轨道入轨点(HOI)或稳定流形射入点(MOI)施加机动.以往关于晕轨道转移轨道的研究主要集中于在晕轨道上的入轨点施加轨道机动[1-3，5-8]，稳定流形只是为转移轨道提供了一个初始猜想，探测器并没有运行在稳定流形上，因此，没有真正利用到稳定流形节省燃料的优势.文献[9]中最早研究了Genesis探测器稳定流形射入代价的优化问题.但其提出的两级微分修正法由于将转移轨道分解成许多段进行优化，因此所需的计算量比较大，而且需要预估轨道转移时间，对初始猜想的准确度要求很高.此外，以往晕轨道入轨点都集中于近地点或远地点附近，很少研究晕轨道上其他入轨点的入轨代价.文献[10]中采用传统的优化方法研究了晕轨道上不同入轨点的入轨代价，但得到的最优解较大.

本文利用基于序优化的微分修正法，研究晕轨道近地点稳定流形射入代价的优化问题以及晕轨道上不同入轨点所需的入轨代价.相比两级微分修正法，本文的算法计算量小，可快速得到合适的初始猜想，且不需要预估轨道转移时间.

1 日-地L1点晕轨道的稳定流形

通常，都是在旋转坐标系中研究三体问题，因此，本文定义的质心旋转坐标系是以日-地系统的公共质心为坐标原点，X轴从太阳指向地球，XY平面为黄道面，Z轴垂直黄道面，并沿着日地围绕公共质心旋转的角速度方向.

稳定流形的计算方法为：首先，在晕轨道上取一点xe，根据与该点相关的状态转移矩阵Φ(T,t0)(即从该点出发，积分一个晕轨道周期T后得到的状态转移矩阵，也称为单值矩阵)计算出对应于稳定特征值λs的稳定特征向量ηs；然后，在邻域上取一点xs+=xe+dηs，其中d为常数，一般取值范围为150km～200km，本文取d=200km；最后，将xs+作为初值逆向积分运动方程即可得到该点的稳定流形.对晕轨道上各点重复上述过程，则得到与晕轨道相关的稳定流形.晕轨道上距离地球最近的点称为近地点，距离地球最远的点称为远地点.图1为质心旋转系下日-地L1点Az振幅(Z轴方向的振幅)为120 000km的晕轨道的稳定流形，加粗黑色轨线为晕轨道近地点的稳定流形.

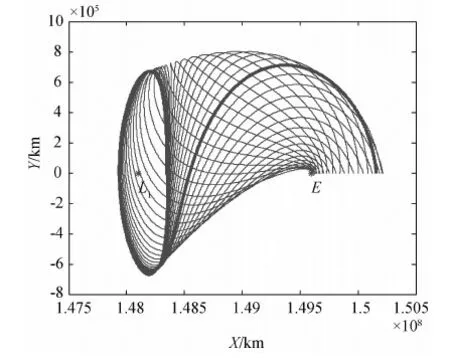
图1 日-地L1点晕轨道的稳定流形

2 节能转移轨道

由于晕轨道入轨速度增量ΔVHOI或者稳定流形射入速度增量ΔVMOI由探测器自身提供，对于漫长的深空探测而言，节省ΔVHOI或ΔVMOI是非常有意义和有必要的.以往的研究主要集中于ΔVHOI的优化的问题，而本文主要研究晕轨道稳定流形射入速度增量ΔVMOI的优化问题，寻找燃料消耗最小的节能转移轨道.

本文选择Az振幅为120 000km的晕轨道作为目标轨道，设计从地球停泊轨道到晕轨道的低能量转移轨道，入轨点为晕轨道的近地点.以近地点稳定流形上M点为界，将地球停泊轨道到晕轨道的转移轨道分为两段：TO1和TO2，其中轨道段TO2在稳定流形上，如图2所示[11].以往的转移轨道设计是本文的一种特殊情况，即M点在晕轨道的近地点.本文的主要目的就是寻找晕轨道近地点稳定流形上合适的位置M点，使所需的晕轨道稳定流形射入速度增量最小.为了便于利用稳定流形设计转移轨道，采用逆向设计，假设转移轨道的初始点在晕轨道或稳定流形上，目标点在地球停泊轨道上.

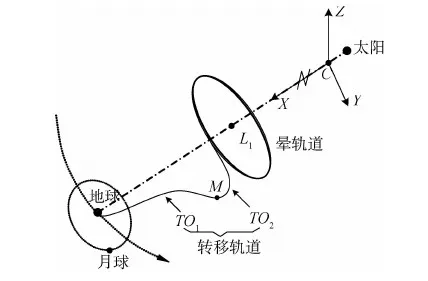
图2 节能转移轨道

3 优化方法

文献[12]将序优化与微分修正法相结合，对晕轨道入轨速度增量ΔVHOI进行优化，得到了燃料消耗和转移时间折衷考虑的转移轨道.本文也采用该方法研究晕轨道稳定流形射入速度增量ΔVMOI的优化问题.传统优化问题都是以寻找问题最优解为目标进行求解，而序优化(OO，ordinal optimization)则以很高的概率寻找足够满意解为目标，进而减小搜索量和难度[13].在数值优化之前引入序优化思想，有效缩小搜索空间，得到足够好的解，将其作为微分修正法的初始猜想，迭代修正得到满足终端精度限制且燃料消耗足够小的解.

仿真中，选择晕轨道近地点作为入轨点，期望的地球停泊轨道高度h*为185km.设速度增量ΔVMOI其中β为速度增量方向角，是质心旋转系XY平面内施加的机动ΔVMOI与X轴的夹角.优化步骤为：首先，按照机会均等原则，在ΔVMOI和β的取值范围内随机抽取N个可行解，采用较大积分步长作为序优化的粗糙模型，可大致估计终端轨道高度差(即实际轨道高度h与期望停泊轨道高度h*之差Δh=h-h*)，根据得到的Δh与ΔVMOI和β的关系图缩小优化空间.然后，在缩小后的优化空间中，随机抽取N个可行解，积分粗糙模型，对N个可行解进行快速粗糙评估，确定该优化问题的有序性能曲线(OPC)类型.依据得到的OPC曲线类型和采样点分布情况，选择燃料消耗小且相应终端位置偏差Δh较小的采样点作为得到的足够好解.之后，采用小积分步长(即序优化中的精确模型)，利用微分修正法对各个足够好解进行迭代修正，选择燃料消耗最小的解作为最终得到满足终端位置精度的解.

4 仿真结果及分析

4.1晕轨道近地点稳定流形射入代价

假设从晕轨道近地点稳定流形逆向出发后ts天(ts=0,1,…,180)施加稳定流形射入速度增量ΔVMOI，利用上述优化方法，得到晕轨道近地点稳定流形不同射入点所需的速度增量如图3所示，部分数据如表1所示.

图3 出发后天数与相应的射入代价之间的关系

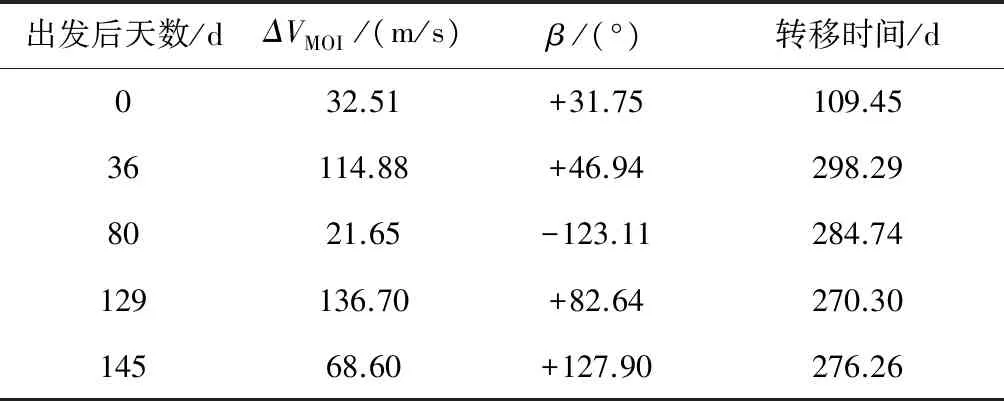
表1 近地点稳定流形不同射入点所需的速度增量

由表1可以看出，沿着晕轨道近地点稳定流形运行约80天时，所需的稳定流形射入速度增量ΔVMOI最小，约21.65m/s就能使探测器到达指定高度的地球停泊轨道，如图4所示.不沿稳定流形运行的转移轨道在晕轨道近地点需施加32.51m/s的晕轨道入轨速度增量ΔVHOI，如图5所示.因此，虽然转移时间增长，但节省约33%的燃料消耗.

图4 射入稳定流形的转移轨道

图5 射入晕轨道近地点的转移轨道

4.2晕轨道上不同点的入轨代价

本文4.1节给出的是借助稳定流形的节能转移轨道，而本节主要研究不借助稳定流形的转移轨道.从晕轨道远地点开始，顺时针将晕轨道按时间30等分，采用上述优化方法对晕轨道上30个等分点的入轨代价进行优化，结果如表2所示，对应的曲线关系如图6所示.仿真中，各个点所需的进入地球停泊轨道的入轨速度增量ΔVTTI约为3.2km/s，差别很小.与Stalos等人采用传统方法得到的结果相比，本文方法得到的最优入轨代价更小，并且得到了等分点16～20的燃料消耗最小转移轨道(简称燃耗最小解)，而Stalos等人只得到了这些点的折衷考虑燃料消耗和转移时间的最优解(简称折衷解).表2中轨道①为折衷解，轨道②为燃耗最小解.

表2 晕轨道部分入轨点所需的速度增量

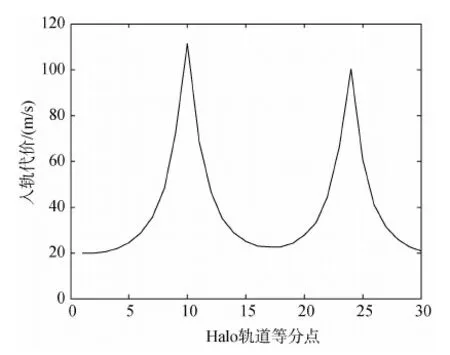
图6 晕轨道上不同点的入轨代价

由表2可知，在不借助稳定流形的情况下，晕轨道近地点入轨的燃耗最小解比折衷解节省约30%的燃料消耗，转移轨道如图7所示.晕轨道远地点附近入轨比近地点附近入轨节省燃料消耗，但转移时间较长.在晕轨道Y轴幅度最大处附近，所需的入轨机动最大，对应的转移轨道如图8和图9所示.

比较表1和表2可知，对于晕轨道近地点入轨而言，借助稳定流形的节能转移轨道在燃耗和转移时间方面都优于不借助稳定流形的燃耗最小解.

图7 晕轨道近地点入轨的燃耗最小转移轨道

图8 入轨点为第10个等分点

图9 入轨点为第24个等分点

5 结论

本文利用基于序优化理论的微分修正法，研究了晕轨道近地点稳定流形轨线上不同射入点所需的燃料消耗，给出了稳定流形上最小速度增量的射入点位置，得到了借助稳定流形的晕轨道近地点入轨的节能转移轨道.该节能转移轨道比晕轨道近地点施加速度增量的折衷解节省约33%的燃料消耗.同时，研究了晕轨道上不同入轨点的入轨代价，得到了不借助稳定流形的晕轨道近地点入轨的燃耗最小转移轨道，该转移轨道比近地点入轨的折衷解节省约30%的燃料消耗.此外，晕轨道远地点入轨比近地点入轨更省燃料.对于晕轨道近地点入轨而言，借助稳定流形的节能转移轨道在燃耗和转移时间方面都优于不借助稳定流形的燃耗最小解.仿真结果验证了本文方法的有效性.利用该方法还可对晕轨道上其他入轨点稳定流形的射入机动进行优化.

[1] Howell K C,Barden B T,Wilson R S,et al.Trajectory design using a dynamical systems approach with application to Genesis [C].AAS/AIAA Astrodynamics Specialist Conference,Sun Valley,Idaho,August,1997

[2] Howell K C,Barden B T,Lo M W.Application of dynamical systems theory to trajectory design for a libration point mission [J].The Journal of the Astronautical Sciences,1997,45(2): 161-178

[3] Lo M W,Williams B G,Bollman W E,Han Dongsuk,et al.Genesis mission design [J].Astronautical Sciences,2001,49(1): 169-184

[4] Farquhar R W.Station-keeping in the vicinity of collinear libration points with an application to a lunar communications problem [C].Space Flight Mechanics Specialist Symposium,Denver,Colorado,1966

[5] Howell K C,Mains D L,Barden B T.Transfer trajectories from earth parking orbits to sun-earth Halo orbits [J].Advances in the Astronautical Sciences,1994,87: 399-422

[6] Rausch R Raou.Earth to Halo orbit transfer trajectories [D].Purdue University,2005,80-83

[7] Li M T,Zheng J H.The optimization of transfer trajectory for small amplitude Halo orbits [J].Measurement and Control,2008,41(3): 81-84[8] 胡少春,孙承启,刘一武.基于不变流形的夸父卫星A轨道设计 [J].航天控制,2009,27(3): 37-41

[9] Wilson R S,Howell K C,Lo M W.Optimization of insertion cost for transfer trajectories to libration point orbits [J].Advances in the Astronautical Sciences,1999,103: 1569-1586

[10] Stalos S,Folta D,Short B,Jen J,Seacord A.Optimum transfer to a large-amplitude Halo orbit for the Solar and Heliospheric Observatory(SOHO) spacecraft [J].Advances in the Astronautical Sciences,1993,84: 639-650

[11] 胡少春,孙承启,刘一武.星际高速公路技术及其在夸父计划中的应用 [J].空间控制技术与应用,2008,34(6): 12-17

[12] 胡少春,孙承启,刘一武.基于序优化理论的晕轨道转移轨道设计 [J].宇航学报,2010,31(3): 662-668

[13] Edward T W L,Ho Y C.Universal alignment probabilities and subset for ordinal optimization [J].Journal of Optimization Theory and Applications,1997,93(3): 455-489

TheOptimizationofTransfertoHaloOrbits

HU Shaochun1,2SUN Chengqi1,2LIU Yiwu1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

Stable manifolds associated with a Halo orbit can be used to design the transfer trajectory from the Earth to Halo orbit.However,previous studies mainly focused on the optimization of Halo orbit insertion maneuver velocity.So,the stable manifolds only serve as an initial guess for use in a transfer trajectory design scheme.The probe didn’t travel on the stable manifolds,and couldn’t make use of the low energy transfer character of manifolds.The differential correction based on Ordinal Optimization theory is used to minimize the stable manifold orbit insertion maneuver velocity in this paper.The numerical simulation results show that the insertion maneuver onto the given stable manifold could save maneuver costs by 33% compared with the Halo perigee insertion maneuver.Moreover,insertion costs for different points in the Halo orbit are analyzed,thus getting the lowest Halo perigee HOI cost transfer trajectory.

libration point; interplanetary superhighway; Halo orbit; stable manifold; ordinal optimization; differential correction