一类卫星推力器布局的多目标优化设计方法

2010-12-11武云丽

空间控制技术与应用 2010年4期

关键词：卫星平台姿态控制推力器

林波，武云丽

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190)

一类卫星推力器布局的多目标优化设计方法

林波1,2，武云丽1,2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京100190)

针对一类卫星平台的推力器布局进行优化方法建模，给出推力器布局设计原则和优化指标，将推力器布局问题转化为一个多约束多目标寻优问题.最后对IntelSat-VII/VIIA推力器布局进行优化设计，优化结果达到了预期效果，验证了本文方法和指标的有效性.

推力器布局；姿态控制；航天器；布局优化

随着现代卫星平台的任务和功能日益多元化，携带的载荷和其他设备越来越复杂，导致卫星平台上各种设备的布局日益复杂，需要考虑的限制条件更多.作为卫星控制系统所需的推力器，安装台数一般多达12台以上，其布局需要考虑推力器羽流、热辐射、以及燃烧物等对整星以及其他有效载荷的影响，因此对其安装位置和安装角度有较为严格的要求.早期的卫星平台结构简单，布局空间余量大，12个推力器一般布置在过卫星质心的三个正交面附近，例如中国的东方红三号卫星平台、北斗二号卫星平台属于这种安装方式，其优点是单个推力器工作时对其他两个轴的干扰力矩较小.随着卫星有效载荷逐步增加，结构也日趋复杂，推力器已不能完全安装在过卫星质心的平面附近.例如，SS/L-1300卫星平台推力器基本安装在星体±Z面的4个顶角附近[1]；日本的DRTS(date relay test satellite)卫星安装了12个推力器，其中4个位于过质心的XOY面内，其余8个推力器也均安装在±Z面上的顶角上[2]；美国基于LS3000平台的IntelSat VII/VIIA卫星[3](布局见图1)东西板上分别安装了4GHz和6GHz的对地固面天线反射器，南北板上安装有大型柔性太阳翼，为了避开推力器对这些部件的影响，12台推力器全部安装在卫星的对地和背地板上，其中有8个推力器装在对地板和背地板的4个角上；中国的东方红四号卫星平台推力器布局也大多安装在卫星±Z面的4个角附近.由于这类卫星平台的推力器安装面不过卫星的质心，因此单个推力器工作时会同时产生两个方向的控制力矩，在进行姿轨控时需要同时开启2个推力器组合使用才能获得期望的控制力矩.

IntelSat VII/VIIA卫星采用的这种推力器布局方式在国内外有广泛应用，本文针对类似平台下的一类卫星的推力器布局和约束条件进行分析，给出推力器布局的优化方法和模型，最后利用优化方法和模型进行了推力器布局设计，获得较好的效果.

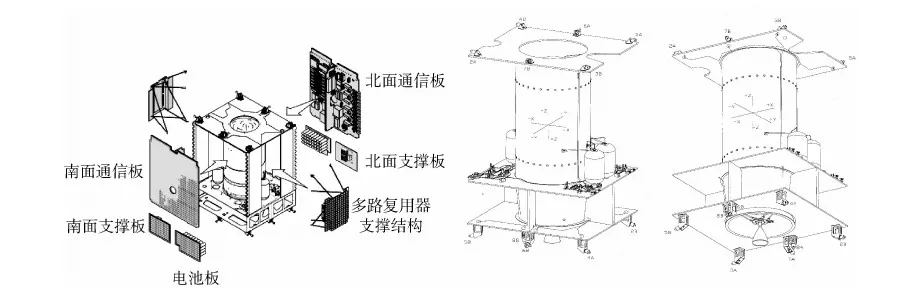
图1 IntelSat VII推力器布局[3]

1 推力器布局模型

定义卫星机械坐标系为：原点位于卫星与运载火箭机械分离面内，原点固联在卫星上，并与星箭分离面上的3个销钉所组成的理论圆的圆心重合，z轴垂直于卫星与运载火箭的连接分离面，其正方向从原点指向对地板，x轴的正方向从原点指向卫星东板，y轴的正方向从原点指向卫星南板.定义卫星本体坐标系为：原点在整星质心，xb、yb和zb3轴分别平行于机械坐标系3个轴.假设单个推力器标称推力为F，推力矢量F=[Fx,Fy,Fz]在卫星本体坐标系中方位角和仰角分别为φ和θ，其中φ∈[0,360°]为推力矢量F在卫星本体系oxbyb平面内与xb轴的夹角，θ∈[-90°,90°]为推力矢量F与卫星本体系oxbyb平面的夹角.Rc=[xc,yc,zc]为整星质心在机械坐标系中的位置矢量.R=[x,y,z]为推力器在机械坐标系中的位置矢量，D=R-Rc=[x-xc,y-yc,z-zc]为推力器在卫星本体坐标系中的位置矢量，见图2.

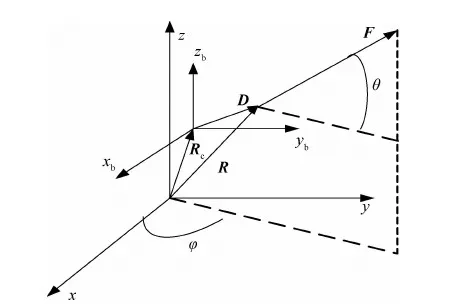
图2 单个推力器推力矢量方位

这里定义Mx,My,Mz分别为推力器产生的三轴力矩；α,β,γ分别为推力矢量F与xb,yb,zb三个轴的夹角，则依据图2可得到上述变量间有如下关系：

α=arccos(cosθcosφ),

β=arccos(cosθsinφ),

γ=arccos(sinθ),

式中，F、D为F、D的模.

安装角度满足约束方程：

安装位置和力矩满足约束方程为：

其中，

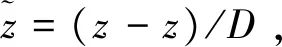
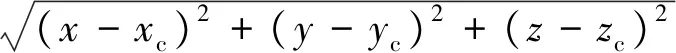
由上述方程可见，单个推力器的安装位置和方位可由位置矢量R和两个方位角φ，θ唯一确定，推力器的布局问题描述为在卫星的可行安装区域和方位范围内寻求一个最佳的S=[x,y,z,φ,θ]，单个推力器其可行区域描述为一组取值区间

x∈[xl,xh],y∈[yl,yh],z∈[zl,zh],

式(7)可简单记为S∈[Sl,Sh].

2 推力器布局组合优化策略

对于卫星系统而言，其控制往往需要多个推力器组合工作，因此除了考虑单个推力器的工作效率外，还需要考虑多个推力器配合使用的问题.例如，卫星在进行轨道控制时需要产生的推力尽可能最大，同时对姿态的干扰力矩尽可能最小；而在进行姿态控制的时候要求产生的控制力矩尽可能最大，同时对卫星位置干扰尽可能最小；此外，布局时还需要避免推力器羽流、燃烧残余物等对相邻设备的影响等.因此，卫星推力器布局为一个多维、多约束条件下的多目标优化问题.

2.1推力器布局原则

本文以IntelSat VII/VIIA推力器布局方式作为例子进行优化，这种布局方式具有广泛代表性.在IntelSat VII/VIIA卫星共安装有12台推力器，A/B两份互为备份，各6台，编号为2A/B、3A/B、4A/B、5A/B、6A/B、7A/B，其位置关系见图1.卫星在轨运行中远地点模式A/B分支都开启，其余模式下A或B分支开启其一.B分支作为A分支的备份.以A分支为例，在进行姿轨控时各个推力器组合如下：

a.2A+3A：向东位保，产生-X向推力-Fx；

b.4A+5A：向西位保，产生+X向推力Fx；

c.2A+4A：姿态控制，产生+Y轴姿态控制力矩+My；

d.3A+5A：姿态控制，产生-Y轴姿态控制力矩-My；

e.2A+5A：姿态控制，产生+Z轴姿态控制力矩+Mz；

f．3A+4A：姿态控制，产生-Z轴姿态控制力矩-Mz.

按上述组合方式可知，2A、3A、4A、5A推力器既要进行轨控又要进行Y轴和Z轴的姿态控制，在布局时需要兼顾考虑.例如，A分支布局需要满足以下原则：

a.2A+3A向东位保时产生-X向的推力最大，而对向南或向北的干扰推力最小；

b.2A+3A向东为保时尽可能在三轴上不产生干扰力矩；

c.4A+5A向西位保时三轴干扰力矩最小；

d.2A+4A应在+Y轴上提供最大的控制力矩,而在另外两轴上产生的力矩最小；

e.3A+5A在应在-Y轴上提供最大的控制力矩,而在另外两轴上产生的力矩最小；

f.2A+5A应在+Z轴上提供最大的控制力矩,而在另外两轴上产生的力矩最小；

g.3A+4A在应在-Z轴上提供最大的控制力矩,而在另外两轴上产生的力矩最小.

此外，还需要考虑推力器附近设备的安装及羽流对周边设备的影响等.对于这些因素，一般可通过限定推力器安装位置的可行域或者安装方位的可行域来达到目的，因此，对于推力器2、3、4、5的安装位置和角度需要进行优化，以满足上述原则.

2.2推力器优化指标设计

依据上述布局原则，设计优化指标如下：

a.位保指标函数

向东位保指标函数为：

向西位保指标函数为：

式中，JF,2A+3A为位保推力指标函数,N为期望的推力值.物理意义是让向东位保推力在X轴尽可能接近N，即满足F2Ax+F3Ax=N，在Y轴和Z轴上产生的推力尽可能接近0，即满足F2Ay+F3Ay=0、F2Az+F3Az=0；JM,2A+3A向东位保干扰力矩指标函数，其物理意义是2A+3A推力器进行向东位保时产生的干扰力矩最小.

b.姿态控制指标函数

式中,JM，2A+4A为Y轴控制力矩指标，物理意义是让2A+4A产生+Y方向期望力矩Mynom，同时让X轴和Z轴上的力矩最小；JM,2A+5A为Z轴控制力矩指标，物理意义是让2A+5A产生+Z方向期望力矩Mznom，同时让X轴和Y轴的力矩最小；

c.综合指标：

式中，ki(i=1,…,6)为加权系数，k1,k2,k3,k4为东西位保指标的加权系数,k5,k6为Y轴和Z轴姿控指标的加权系数，可依据实际应用调整某个指标的权重.一般情况下，卫星在长期运行期间推力器主要用于进行位置保持和角动量卸载，而通常进行位置保持所消耗的推进剂比进行卸载消耗的要多，因此同步轨道段主要应考虑提高位置保持的效率，即系数k1,k2,k3,k4应选择较大，而k5,k6系数则相应小一些.

推力器布局问题最终转化为寻求一组X=[S2A,S3A,S4A,S5A]使式(15)表示的指标最小：

J=minF(X)=min{k1F2+3+k2M2+3+k3F4+5+k4M4+5+k5M2+4+k6M2+5},

2.3优化算法

对于2.2节所描述的优化问题，求解方法较多.例如，有基于粒子群的多目标优化算法[4]、遗传算法等[5]，该类算法特点是使用种群、适应值以及繁衍等概念，容易在可行区间能寻求的全局最优解，缺点是计算量大，计算时间消耗多；另外还有基于梯度的算法，如牛顿内点法[6-7]，共轭梯度法等，该类方法求解速度快，对于非凸集则会求解得到局部最优解，优点是算法成熟且在Matlab等商业软件中有优化工具箱.针对具有不等式约束优化问题Matlab提供了一个通用的求解函数fmincon(x)，使用者只需要给出指标描述函数和优化变量的约束条件就可求解.本文利用Matlab提供的函数进行优化计算.Matlab提供的fmincon(x)函数能够对式(16)～(18)描述的多重约束问题进行优化:

优化向量X满足:

式中,f(X)为优化目标函数,g(X)为不等式约束，h(X)为等式约束，且g(X)和h(X)可为向量X的非线性函数.

对于式(16)～(18)的约束优化问题，通过Lagrangian乘子法转化为式(19)描述的无约束优化问题，利用梯度法求解.

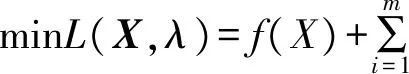
梯度法计算步骤如下：

Step1: 给定初始点X0和收敛精度ε，

Step2: 计算第k步的梯度ΔL(Xk,λ)，

Step3: 令dk=-ΔL(Xk,λ)，

Step5:Xk+1=Xk+σdk，

Step6: 若‖ΔL(Xk,λ)‖≤ε，则X*=Xk.

退出计算，否则，转入Step2继续迭代.

梯度法是fmincon(x)函数可选的求解方法之一，还可以通过Matlab提供的optimset函数设置其他求解方法.

3 推力器布局优化算例

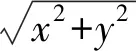
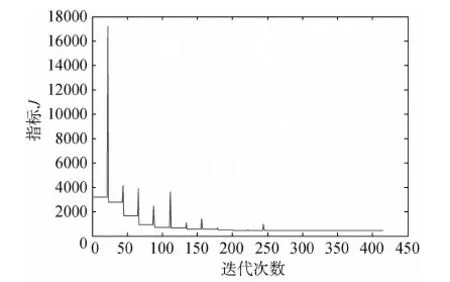
图3 指标收敛曲线

优化前后的安装位置和安装角度见表2，优化前后推力和力矩见表3.表2中，优化前推力器4A不满足表1给定的约束范围，优化后位置和角度均满足位置和角度约束.表3中，以+Y轴姿态控制为例，优化前在X轴上产生约-6.18N·m的干扰力矩，在Z轴产生约-7.055N·m的干扰力矩，优化后干扰力矩大幅降低，X轴约3.38N·m，Z轴约-0.73N·m；Y轴姿控力矩达到约27N·m，Z轴姿控力矩达到约14N·m，优化前后控制力矩改善明显；优化后向东位保时产生18.46N的推力，在三轴上产生的力矩不大于0.6N·m，向西位保产生-15.76N的推力，在Y轴约-1.28N·m的力矩，约为Y轴控制力矩的5%，对姿态控制影响不大.

表1 推力器安装位置和方位角约束范围

表2 优化后的安装位置和安装角度

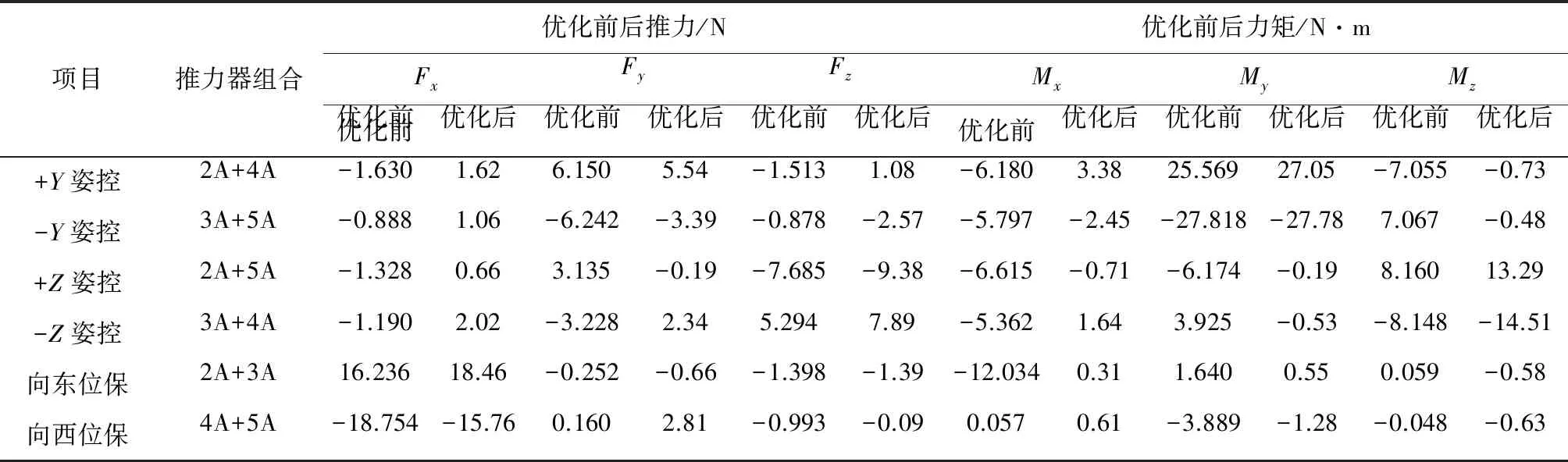
表3 优化后的推力器组合产生的推力和力矩

4 结论

本文针对一类卫星平台的推力器布局问题进行了优化设计，给出了优化设计原则和优化指标，将推力器布局问题描述为一个多目标优化问题，通过计算机在可行区域内寻优，避免了通过人工试凑调整布局的不足.并基于文中的设计原则和指标对IntelSat-VII/VIIA卫星的推力器布局进行了优化设计，获得了良好的效果.

[1] David J K,Jonathan C W.SS/L-1300 satellite optimized for land launch[R].AIAA 2006-5302

[2] Hitoshi K.Activities on electric propulsion in Japan-space flight from basic research[C].The 38thAIAA Joint Propulsion Conference and Exhibit,Indianapolis,Indiana,July 7-10,2002

[3] John C H,Peter G.Earth acquisition and attitude recovery for IntelSat VII/VIIA Satellites[C].The 20thAIAA International Communication System Conference and Exhibit,Montreal,Quebec,Canada,May 12-15,2002

[4] 邹卫强,卜质琼.一种基于智能群的快速多目标优化算法[J].计算机工程与应用，2008,44(6): 59-61

[5] 赵亮,雎刚,吕剑虹.一种改进的遗传多目标优化算法及其应用[J].中国电机工程学报,2008,28(2):96-102

[6] Coleman T F,Li Y.An interior,trust region approach for nonlinear minimization subject to bounds [J].SIAM Journal on Optimization,1996,6(2):418-445

[7] Coleman T F,Li Y.On the convergence of reflective Newton methods for large-scale nonlinear minimization subject to bounds [J].Mathematical Programming,1994,67(2): 189-224

AMulti-ObjectiveOptimizationMethodofThrusterConfigurationforaClassofSatellite

LIN Bo1,2,WU Yunli1,2

(1.BejingInstituteofControlEngineering,Beijing100190,China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

A multi-objective optimization method for thrusters configuration is proposed for a class of satellites.In the paper,several optimization goals and design criterion are given for positioning and orienting thrusters.The position and the orientation of thrusters are achieved by solving the multi-objective optimization problem.Finally,the method is used to achieve positioning and oriening of thrusters for IntelSat-VII/VIIA,the results show the method is valid.

thruster configuration; attitude control; spacecraft; configuration optimization