基于特征模型的再入飞行器制导律设计*

2010-12-11张钊,胡军,王勇

空间控制技术与应用 2010年4期

关键词：倾斜角航程方位角

张钊,胡军,王勇

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

基于特征模型的再入飞行器制导律设计*

张钊1,2,胡军1,王勇1,2

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190)

研究了一种大升阻比的高超声速飞行器的再入制导问题.应用基于特征模型的自适应控制理论，提出了一种跟踪参考阻力加速度的制导方法，同时通过跟踪飞行方位角，来修正飞行器侧向航程.这种基于特征模型的自适应控制方法不需要通过数据拟合来获得气动升力与阻力的解析表达式，克服了飞行器在再入飞行中，气动数据不断变化时造成的困难.通过跟踪飞行方位角来修正倾斜角指令，可以获得比倾斜角翻转方法更精细的对侧向航程的控制能力.六自由度仿真结果表明，文中设计的制导方法可以达到调整侧向航程的目的，但其代价是损失总航程.

再入制导；特征模型；阻力加速度

面对称外形的再入飞行器，由于具有更大的升阻比，因而在大气中具备更强的平衡滑翔能力和更强的机动性能.设计恰当的GNC系统，此类飞行器能够以小的峰值阻力加速度返回，水平方式着陆，为航天器的重复使用提供了必要前提[1-2].当再入初始条件有较大偏差或返回过程中遇到大的扰动时，高升阻比飞行器具有更强的鲁棒性能.这些特点使得此类飞行器成为当前研究的热点，其优势的发挥需要相应的制导方法来保证.

跟踪参考阻力加速度的再入制导方法，在航天飞机及其后一系列技术验证机的再入制导中得到了成功的应用[2-4].该方法根据飞行器再入初始条件以及终端条件，在动压、过载、热流等约束条件下，离线设计一条参考阻力加速度剖面.再入过程中，根据位置速度偏差，在线调整参考阻力加速度剖面，同时利用PID或反馈线性化方法，设计倾斜角指令来跟踪期望阻力加速度.当阻力加速度小于期望值时，增大飞行器的倾斜角，减小升力在竖直方向上的分量，从而使飞行器加速飞向稠密的大气层.而当阻力加速度大于期望值时，减小倾斜角增加升力在竖直方向上的分量，从而减缓飞行器下落的速度甚至提高飞行高度.但无论是线性方法还是非线性的反馈线性化方法，其控制精度都依赖于模型的精确性.这使得依赖于模型的阻力加速度跟踪制导方法的适应性较差，无法适应更加灵活的任务要求.

跟踪阻力加速度只能确定倾斜角的大小而不能确定其正负.为了确定倾斜角符号，传统的做法是利用倾斜角翻转逻辑.恰当地设计该逻辑，可以使侧向航程满足终端要求.当倾斜角在再入过程中恒为正或负时，对应了在一定攻角剖面下的最大侧向航程能力.如果牺牲一些阻力加速度跟踪的性能，则可以在不调整攻角的情况下获得更大的侧向航程控制能力.

为了解决传统阻力加速度跟踪方法依赖于模型精度的问题，本文提出一种基于特征模型的自适应再入制导方法[5-6]，同时，利用飞行方位角跟踪来调整侧向航程.首先将阻力加速度看作以倾斜角的余弦为输入的二阶特征模型输出，而将飞行方位角看作以倾斜角的正弦为输入的一阶特征模型输出.利用梯度法辨识出特征模型的时变参数，分别设计阻力加速度和飞行方位角的跟踪控制器.最后将两个跟踪控制器获得的期望倾斜角做线性加权，得到输出给控制器的倾斜角指令.通过对一种大升阻比的高超声速飞行器的六自由度仿真，验证了本方法的合理可靠性，并且研究了加权系数选取对航程的影响.

1 再入飞行器质心动力学方程

由于制导律研究的是飞行器质心运动规律，首先给出刚体三自由度质心动力学方程组[1]

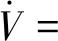
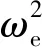
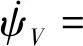
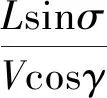
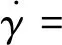
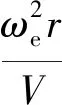
式中：r为飞行器质心到地心的距离；φc与λ分别为飞行器所在位置的经度与纬度；V为飞行器相对于地球表面的速度的大小；ψV为速度在当地水平面上的投影与正北方向的夹角，称为飞行方位角；γ为速度方向与当地水平平面的夹角，称为爬升角；D为阻力加速度，与飞行器速度方向相反；L为升力加速度，位于飞行器纵向对称平面内且垂直于速度方向；σ为倾斜角，是升力方向与包含飞行器速度矢量的铅垂面的夹角；ωe为地球自转角速度.

飞行器受到的气动升力加速度L和阻力加速度D，可用无量纲的升力系数CL和阻力系数CD计算如下：

式中，m为飞行器的质量，ρ为大气密度，S为参考面积.

注1.通常大气内飞行器的升力系数和阻力系数可以通过空气动力学计算、风洞试验和飞行试验获得，并以数据表格的形式给出.一般可以简单的认为气动力系数是马赫数、高度、攻角和侧滑角等量的函数.其解析形式在近似的情况下，可以通过数据拟合得到.

注2.大气密度是具有很大不确定性的量，受到高度、日照条件和地表物理状况等很多因素的影响.仿真中，通常将大气按照高度分层，在每层用线性插值得到不同高度的密度数据.而在分析时，通常用简化的指数形式大气密度，模型如下：

其中，hs为特征常数.

2 制导律控制变量的选取

注意到飞行器再入过程中，阻力加速度的方向总是与速度方向相反，而升力加速度的方向则垂直于速度.这样，阻力在飞行器返回过程中总是作负功，而升力则不作功.根据力乘以速度等于功率可知，阻力加速度乘以速度反映了机械能的耗散速率.如果飞行器再入过程中理想地跟踪了以速度为自变量的阻力加速度曲线，则可以按照期望的速率消耗机械能.在再入的过程中，速度变量是单调下降的且其初始值和终端值也比较固定，因此利用速度作为自变量规划参考阻力加速度具有一定的方便性.为了实现对阻力加速度的跟踪控制，下面在忽略地球自转的条件下推导其微分方程.

2.1阻力加速度微分方程

对式(8)求导，得到

两边同时除以阻力加速度表达式，

注意到

r=r0+h

则有

代入式(1)，得到

而

将式(4)、式(13)和式(14)代入式(11)，得到

上式两端对时间求导，有

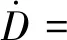
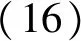
其中控制量u取为

u=-cosσ，

式(16)中各项系数如下：

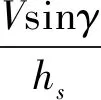
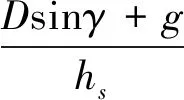
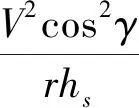
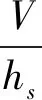
如果上述模型精确，且模型中f1、f2和g1均可精确获得，则阻力加速度跟踪可以应用各种基于模型的设计方法解决.注意到，原始的非线性模型中，存在表征大气密度的特征常数hs，升力加速度，阻力系数以及其一阶和二阶导数项.这些量在实际中是难以精确获得的.此外，对于阻力加速度跟踪回路，其控制变量为倾斜角的余弦.由于倾斜角是在内环姿态控制系统的驱动下改变的，不可能理想的跟踪动态指令，这也会给阻力加速度跟踪系统带来动态不确定性.

由于这些不确定性的存在，使得基于模型的跟踪控制器性能下降，严重时可能出现失稳的情况.传统的方法在理论上不能保证系统性能，而当飞行器的任务发生变化时，设计参数又需要重新调整，给设计人员带来了额外的工作量.基于特征模型的自适应控制方法，则可以从机理上克服上述困难.

2.2飞行方位角

上面讨论的跟踪阻力加速度的设计方案，只能确定倾斜角的大小.为了确定其方向，需要根据侧向航程的约束，设计倾斜角翻转逻辑[2-3].这样能够保证飞行器不会在侧向偏离目标位置过远.通过分析侧向航程的计算公式，可以发现，如果在跟踪参考阻力加速度的过程中，同时跟踪一个参考飞行方位角指令，则可以在一定范围内调整侧向航程.

设初始时刻包含飞行器标称速度矢量的铅垂平面为PI，此平面与正北方向夹角为ψV0，在飞行过程中，设飞行器偏离PI的侧向航程为sy，则

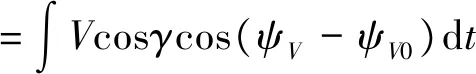
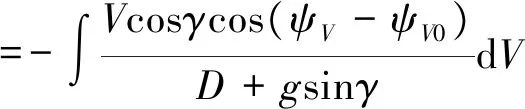
在关心的飞行过程中，爬升角较小，引入近似sinγ≈0，cosγ≈1，有

如果阻力加速度完全跟踪了参考阻力(是速度V的函数)，则侧向航程由飞行方位角ψV决定.如果设计控制律，使得飞行器的飞行方位角满足一定的指令要求，就可以修正侧向航程.根据式(5)，记

u=sinσ，

则有

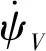
其中

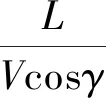
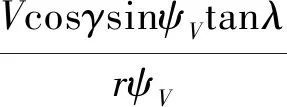
3 基于特征模型的再入制导

特征建模是结合对象动力学特征和控制性能要求的一种新的被控对象建模理论，可以克服动力学建模不考虑控制性能以及在构造控制器时不考虑动力学特征的片面性，从而得到一个好的结果，为复杂对象进行低阶控制器与智能控制器设计提供了理论依据[5].这里给出基于特征模型的阻力加速度跟踪控制方案.

设制导律的采样周期为T，将式(16)离散化，

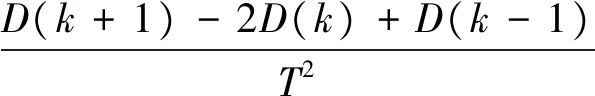
D(k+1)=(2+Tf1+T2f2)D(k)-

(1+Tf1)D(k-1)+T2g1u(k)+T2Δ(k),

忽略误差，得到如下形式的时变差分方程

D(k+1)=f1(k)D(k)+f2(k)D(k-1)+

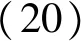
注意这里离散化后的f1(k)、f2(k)和g1(k)与式(16)中的f1、f2和g1不同.采样时间足够小时，f1(k)取值在2附近，而f2(k)在-1附近.

同样，将式(19)离散化，得到

为了估计式(20)和(21)中的参数，采用梯度法辨识.以式(20)的参数辨识为例，记

被估计参数向量

则梯度法参数递推公式为

θ(k)=θ(k-1)+

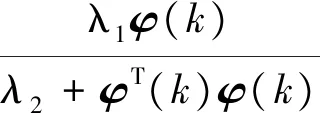
其中λ1，λ2是正常数.

利用梯度法获得被控对象参数估计后，对阻力加速度跟踪回路，设计维持/跟踪控制律，线性反馈控制律，逻辑微分控制律和定常偏置，如下：

上述式中，λ3为小正数，

e(k)=D(k)-Dr(k)，

在逻辑微分控制律中，

c′为常数.则总的控制量uD(k)如下：

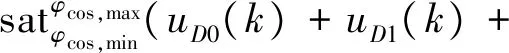
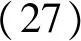
其中

这里对控制量取一个范围限制，可以防止滚动角过大引起飞行器以较大速度进入稠密大气.这样指令滚动角用如下方法计算：

其中Lsgn=±1，是根据倾斜角翻转逻辑确定的符号量，本文仿真中为了研究跟踪飞行方位角对航程的影响，将简单的取Lsgn=1.

类似的，对飞行方位角跟踪回路，设计维持/跟踪控制律，线性反馈控制律和积分形式的控制律如下：

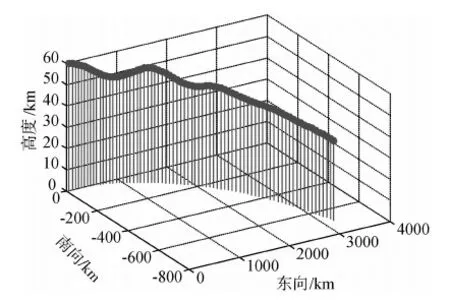
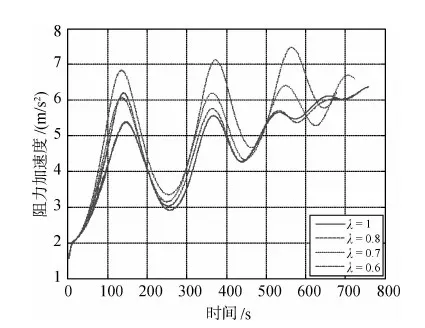
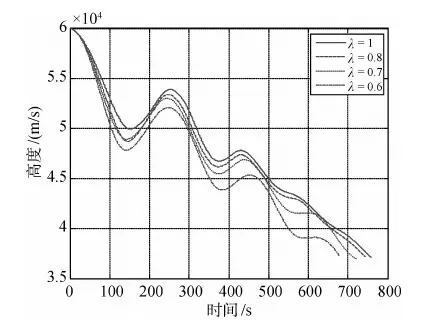
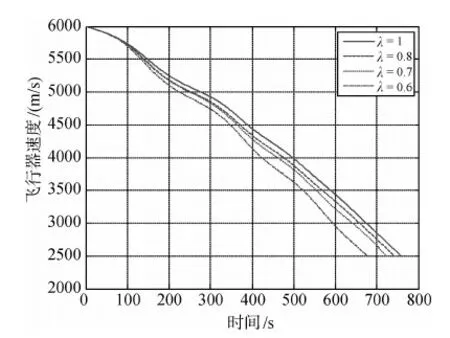
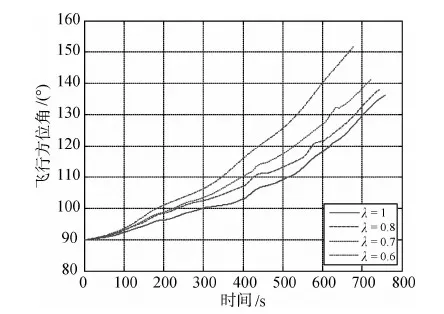
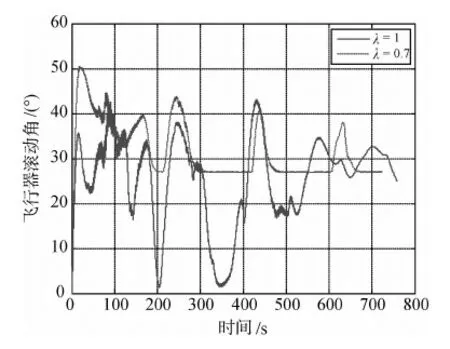
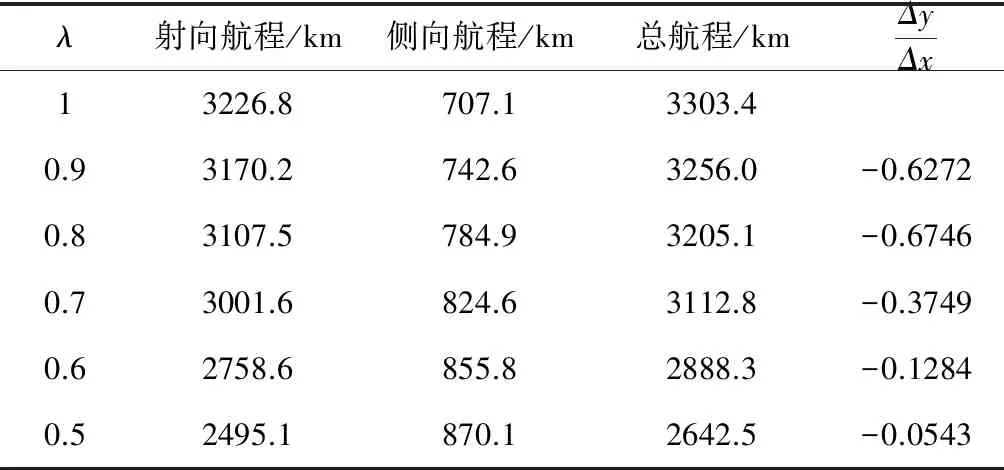
其中，l3为线性反馈系数，用于配置系统的闭环极点，取0

其中

这里积分形式的控制律用于消除侧向航程偏差.

式(28)和(33)分别根据跟踪参考阻力加速度与参考飞行方位角，得到两个期望的倾斜角指令，实际制导律输出给控制器的倾斜角控制指令通过线性加权得到，如下所示

其中λ为根据任务需要而设定的加权系数.

4 数学仿真

本文的仿真对象，是一种大升阻比的高超声速飞行器.该飞行器具有4个独立的控制舵面，分别为左、右升降舵和左、右方向舵.气动力数据表格包括轴向力系数Cx，侧向力系数Cy，法向力系数Cz，滚转力矩系数Cl，俯仰力矩系数Cm，偏航力矩系数Cn，这些系数通过马赫数、高度、攻角、侧滑角及气动舵偏转角等插值获得.

为了验证文中设计的跟踪阻力加速度的制导律的效果，以及跟踪飞行方位角的制导方法对侧向航程的修正能力，本文设计了如下的六自由度仿真.飞行器初始高度为60km，速度为6km/s水平向东，初始攻角为0°.控制系统跟踪10°功角信号，同时跟踪利用前述制导律给出倾斜角指令，倾斜角符号始终为正，仿真终止条件为速度小于1.5km/s.仿真结果如图1～6所示.

图1 飞行器再入三维航迹图

图2 取不同加权系数时得到的阻力加速度跟踪结果

图3 高度变化曲线

图1给出了权系数为1时，飞行器三维航迹图，图中将地球表面展开成水平面，三轴分别表示高度、东向和南向.由于文中研究的飞行器具有较大的升阻比，使得飞行器在飞行过程中，可以提升高度，从而增加航程.图2给出了取不同的定常加权系数时阻力加速度的跟踪结果.由于飞行器的质心动力学具有大的时间常数，阻力加速度的跟踪出现了一定的起伏.当飞行器的实际阻力加速度小于参考值时，飞行器被控制滚转，使得升力在竖直方向的分量减小.飞行器加速向下运动，进入较稠密大气，阻力加速度加大.当阻力加速度大于参考值时，飞行器又被控制向0°方向滚转，从而增大升力在竖直方向的分量.由于飞行器加速度的改变要通过两次积分才能体现在位置改变和升力向上后，高度依然是下降的，这样阻力加速度会进一步增大.正是这种惯性导致了阻力加速度的震荡，也体现在高度的震荡上，如图3所示.

图4 速度变化曲线

图5 飞行方位角曲线

图6 滚动角跟踪曲线

图4给出了不同加权系数时速度的变化曲线，图5为飞行方位角的变化曲线，图6给出了飞行器实际滚动角曲线.由于单纯跟踪阻力加速度时，飞行器向右翻转不足以跟上期望的飞行方位角.文中设计的飞行方位角跟踪控制指令，倾向于使得飞行器进一步向南偏转.这要增大倾斜角，从而导致飞行器高度下降的更快.当需要减小倾斜角，以提升高度减小阻力加速度时，跟踪飞行方位角的要求又增大了倾斜角，导致飞行器爬升高度降低.

仿真时加权因子的取值从0.5至1.当加权因子逐渐减小时，跟踪阻力加速度的指令在实际制导指令输出中所占的比重逐渐减小.其结果是阻力加速度曲线的震荡加大，仿真中出现的第一个阻力加速度最大值幅值提高，在飞行的后段中也能明显的表现出阻力加速度震荡加剧的现象.对应在高度曲线上，则是飞行器航迹在高度驻点的值逐次降低.由于飞行器飞行高度下降，造成阻力加速度增大，从而使飞行器消耗了更多的机械能.由于机械能消耗，速度也随着加权因子的减小更快的减小.这样随着加权因子的减小，总航程(终点与初始点的水平距离)也减小，而侧向航程则增大.即侧向航程的增大是以总航程的缩短为代价的，这也是由于放宽了阻力加速度跟踪控制的性能所带来的影响.表1给出了加权因子取不同值时仿真得到的航程数据.从表中可见，加权因子选取的越小，射向航程越短，而相应的侧向航程则越长，考虑到跟踪飞行方位角后对总航程造成的损失，加权因子的选取不宜过小，通常在0.7以内较为合适.

表1 仿真结束时飞行器航程数据

5 结论

本文根据再入制导要消耗飞行器机械能的要求，设计了跟踪阻力加速度曲线的制导方法，同时利用侧向跟踪飞行方位角曲线的方法来进一步修正侧向航程.该方法首先将阻力加速度看作以倾斜角的余弦为输入的二阶特征模型的输出，将飞行方位角看作以倾斜角的正弦为输入的一阶特征模型的输出.利用梯度法辨识出特征模型的时变参数，分别设计阻力加速度和飞行方位角的跟踪控制器.最后将两个跟踪控制器获得的期望倾斜角做线性加权，得到输出给控制器的倾斜角指令.这种基于特征模型的自适应再入制导方法，不需要已知解析形式的气动系数模型，利用参数辨识方法自动获取制导律设计中需要的特征参量.与传统的基于模型的制导律设计方向法相比，更简单可行.通过一种高超声速飞行器的六自由度仿真，验证了本方法的合理可靠性.仿真结果显示，通过跟踪飞行方位角的方法来对制导指令进行加权，可以实现对侧向航程进行修正的目标.

[1] 王希季.航天器进入与返回技术(上册)[M].北京: 宇航出版社，1991

[2] Mease K D,Kremer J P.Shuttle entry guidance revisited[C].AIAA Guidance Navigation and Control Conference,Hilton Head Island,Aug 10-12，1992.

[3] Mease K D,Chen D T.Reduced-order entry trajectory planning for acceleration guidance[J].Journal of Guidance,Control and Dynamics,2002,25(2): 257-266

[4] Lu P.Predictor-corrector entry guidance for low-lift vehicles[J].Journal of Guidance,Control and Dynamics,2008,31(4): 1067-1075

[5] 吴宏鑫,胡军,解永春.基于特征模型的智能自适应控制[M],北京: 中国科学技术出版社,2008

[6] 胡军.载人飞船全系数自适应再入升力控制[J].宇航学报,1998,19(1): 8-12

CharacteristicModel-BasedReentryVehicleGuidanceLawDesign

ZHANG Zhao1,2,HU Jun1,WANG Yong1,2

(1.BeijingInstituteofControlEngineering,Beijing100190,China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

A novel drag acceleration tracking guidance law is proposed for a hypersonic reentry vehicle with high lift-drag ratio.By applying the characteristic model-based adaptive control method,a drag acceleration tracking guidance method is proposed together with a flight azimuth angle tracking used to modify lateral distance.The characteristic model-based adaptive control method do not need the analytical form of the aerodynamic lift and drag forces,which are often obtained by curve fitting of the trimmed flight data.This is especially advantageous when the reentry vehicle makes a flight through a large regime and the aerodynamic parameters vary greatly.The flight azimuth angle tracking command is used to modify the banking command,thus changing the lateral distance slightly without bank reversal.Six degree-of-freedom simulation results demonstrated that the guidance law proposed in this paper is effective but at the cost of the loss of total distance.

reentry guidance; characteristic model; drag acceleration