基于有限元的某多管火箭炮模态分析*
2010-12-07徐立黄张贵林张波涛谢家松
徐立黄,张贵林,张波涛,谢家松
(1南京理工大学机械工程学院,南京 210094;2湖北江山重工有限责任公司,湖北襄樊 441003)
0 引言
火箭炮是现代战争中重要的压制性武器,但受射击精度影响,限制了其应用范围。影响射击精度的主要因素之一是发射系统的振动,设法减少火箭炮发射瞬间的振动,将有效的减小火箭弹起始段的扰动,提高火箭炮的射击密集度。要减小发射系统振动对射击精度的影响,甚至利用发射系统的振动补偿其他扰动因素造成的不利影响,首先必须了解和掌握其固有振动特性,以利于火箭炮结构的优化设计和改进。通过ANSYS对火箭炮进行模态分析,得到结构的固有频率和振型,能为某多管火箭炮的振动特性分析和结构动力学特性的优化设计提供依据。
1 模态分析的基本理论
模态分析理论吸取了振动理论、信号分析、数据处理、数理统计及自动控制理论中的有关“营养”,结合自身内容的发展,形成了一套独特的理论。自动控制中的传递函数概念的引入,对模态分析理论的发展起着很大的推动作用。
模态分析的核心内容是确定描述系统动态特性的参数。对于一个有N个自由度的线性系统,其运动微分方程为:
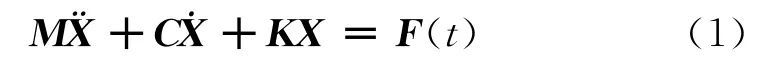
对于自由振动(F(t)=0),上式可写为:

若忽略阻尼影响,式(2)可进一步简化为:
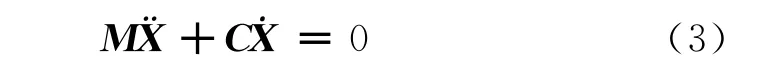
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;X为位移向量;F(t)为作用力向量;t为时间。
自由振动时,结构上各点作简谐振动,各节点位移为:

由式(3)、式(4)得:

2 建立有限元模型
由于火箭炮结构复杂,在ANSYS中直接建模难度较大,文中选用Pr o/E建立实体模型,然后直接导入ANSYS。合理简化后的实体模型见图1,有限元模型见图2。
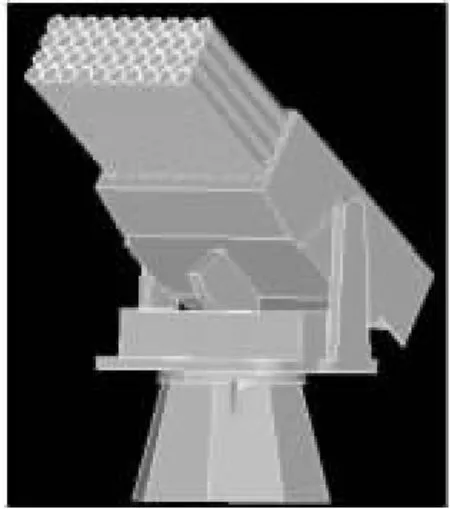
图1 物理模型

图2 有限元模型
建立物理模型时,需对火箭炮进行合理简化,其原则是简化不能影响结构的实际动力学特性。遵循这一原则,忽略结构中的一些圆角、倒角、螺纹孔等。考虑射击时回转与俯仰方向均被锁定,因此将箱体与回转体之间用于调整俯仰角的扇形齿轮简化为刚性连接,耳轴与回转体之间的轴承连接也简化为刚性连接。
整个模型采用由20个节点定义的SOLID95单元,它能够吸收不规则形状的单元而精度没有损失。SOLID95单元有可并立的位移形状并且对于曲线边界的模型能很好的适应,因此非常适合于复杂模型和由CAD导入的模型。模态分析对网格质量的要求与静力学分析并无大的区别,但可以忽略应力集中处对网格的细化处理,更加注重网格的均匀性,这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
定向管为薄壁长圆管,若采用自由网格划分则产生的单元数太多,计算耗时,甚至导致一般计算机无法进行计算。为减少单元和节点,定向管采用扫掠法划分网格,为保证与支撑板部分网格正确连接,将定向管沿支撑板面切割后再划分网格。其余部分结构不规则,均采用自由网格划分。对20节点单元退化为四面体单元的,将其转化为10节点的SOLID92单元。通过划分网格,共产生45460个单元,166075个节点。
整炮均为钢材,其密度为7830kg/m3,弹性模量为209GPa,泊松比为0.3。模拟发射角为45°。这里需要强调的是ANSYS中单位制(Units)问题,ANSYS中有一个只能从命令行输入的命令:“/UNIT,SI”,它的作用仅是标记作用,让用户有个地方做标记,它没有任何单位转换的功能。这要求单位由用户去统一,这类似于振动实验中的标定问题。如果在Pr o/E中建模的长度单位为 mm,这与密度单位kg/m3不符合。若在材料属性中直接输入7830,必将导致模型质量太大,模态固有频率太小。有人提出对密度单位进行换算。由牛顿第二定律F=Ma可知,1 N=1kg*m/s2,那么质量单位应该用吨,相应的密度单位就应该是吨每立方毫米了。但问题并未因此得到完美的解决,因为这时的弹性模量也需要调整,否则结果依旧会失常。文中采用在Pr o/E中建立模型的时候把单位改成国际单位制,同时,在装配时调入模型之前先把装配的模板的单位改成国际单位制,这样,调入ANSYS中的单位就没有问题了。
3 模态计算及分析
有限元模型建好后,进入ANSYS求解器,选择分析类型为 Modal,在求解选项(GUI-Analysis Options)中指定模态提取方法为Block Lanzcos。这种模态提取方法采用Lanzcos算法,用一组向量来实现Lanzcos递归计算,同Subspace法相比,计算精度相当,但速度要快,存储要求较低,只是所需内存比Subspace法多50%。无论用EQSLV命令指定过哪一种求解器进行求解,Block Lanzcos法都将自动采用稀疏矩阵方程求解器。当计算某系统特征值谱所包含的一定范围的固有频率时,采用这种方法特别有效。计算时,求解从频率谱中间位置到高频范围内的固有频率时的求解收敛速度和求解低阶频率时基本相同,因此当采用频移频率FREQB来提取从FREQB起始的n阶模态时,该法提取大于FREQB的n阶模态和提取n阶低阶模态的速度基本相同。同Subspace法一样,Block Lanzcos法特别适用于大型对称特征值求解问题。点击确定按钮,在随后弹出的对话框中设置提取模态数No.of modes to extract为12。为了在后处理器中查看振型,必须进行模态扩展(也就是将振型写入结果文件)。将Expansion Pass On/Off设置为ON。在number of Modes to Expand中指定要扩展的模态数。这里将其设置为12(与提取模态数相同),设置完成后,通过 Main Menu-Sol ution-Current LS对所建立的有限元模型进行计算。
通过计算,得到了模型的前12阶模态,由于从第6阶模态起出现局部模态,且为集中在定向器上的高阶模态,因此这里只对前6阶主要模态进行分析,详见表1和图3~图8,图中位移仅表示振型,非实际位移尺寸。
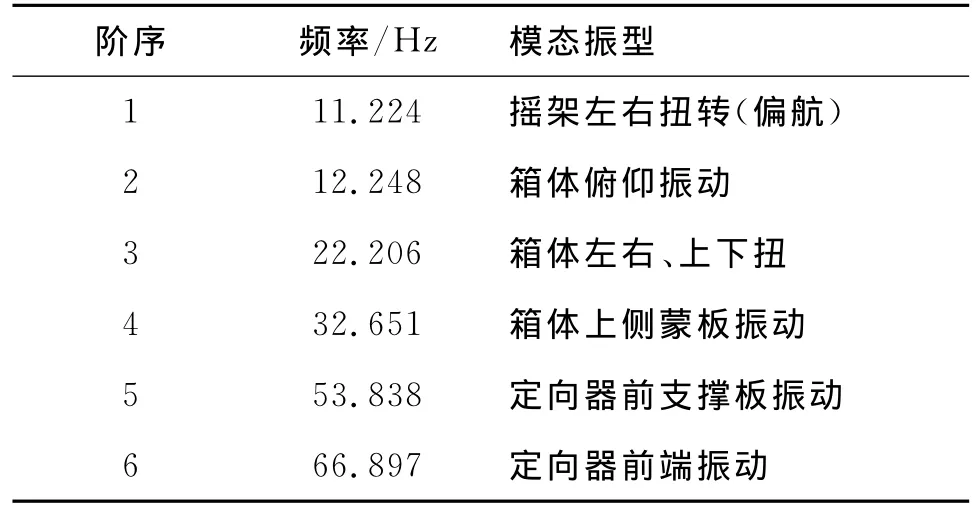
表1 固有频率和振型
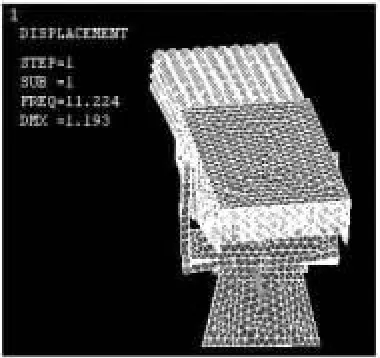
图3 一阶模态振型
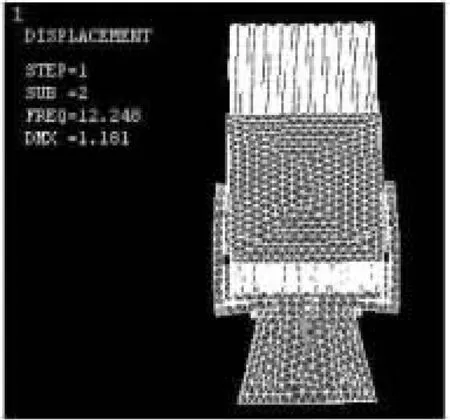
图4 二阶模态振型

图5 三阶模态振型

图6 四阶模态振型
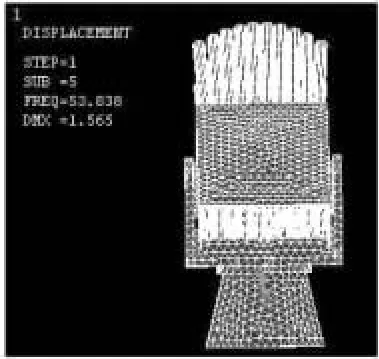
图7 五阶模态振型

图8 六阶模态振型
4 结论
1)该模态分析结果与同类武器(参考文献[4])相符合,证明计算结果的正确性。因此可作为谐谱响应分析、频谱分析等其他动力学分析的基础。可以为该火箭炮结构动力特性的优化设计提供理论依据,从而缩短研发周期,降低研发费用。
2)火箭炮发射时间间隔一般约为0.5s,即频率为2 Hz左右,该发射系统主振频率较好的避开了2 Hz及其邻近倍频。但考虑偏航和俯仰振动对射击精度的敏感性,建议加强摇架的扭转刚度和箱体俯仰连接刚度。如可将箱体底部加厚钢板改为钢架结构,从而减轻质量,提高固有频率。
[1] 傅志方.振动模态分析与参数辨识[M].北京:机械工业出版社,1990.
[2] 刘相新 孟宪颐.ANSYS基础与应用教程[M].北京:科学出版社,2005.
[3] 张琪,刘莉.导弹固有特性的有限元分析[J].弹箭与制导学报,2008,28(2):6-7.
[4] 潘宏侠,王福明.某火箭炮模态试验分析及动态修改[J].兵工学报武器分册.1993(3):58-64.
