药型罩锥角对有利炸高影响的数值分析＊

陈 威，李吉峰，2，朱 磊

（1装甲兵工程学院，北京 100072；2 75131部队，广西贵港 537100）

0 引言

聚能射流侵彻靶板过程是一个瞬态高速的物理化学力学过程，采用计算机模拟的方法进行战斗部设计研究且与试验相比，具有以下优点：周期短、费用低、可重复；可获得任意所需数据；不受时间、空间、气候等条件的限制，可以随时进行。

艾克尔伯格研究炸高和侵彻深度之间的关系，认为一个战斗部存在一个与之相对应的炸高，称为最佳炸高。在此最佳炸高时侵彻深度最大，大于或小于此炸高时侵彻深度都相应减小。由于没有具体的函数或公式，一般通过大量试验获取有利炸高，但费用成本较高。

文献［1］通过大量实验得到“有利炸高随罩锥角的增加而增加”的结论。文中通过对弹塑性流体动力学的深人研究，运用AUTODYN－2D有限元分析软件建立合理的数值计算仿真模型，分别对不同锥角的药型罩形成射流侵彻钢靶板过程进行了数值模拟，把模拟结果和文献［1］得到的结论相对比，验证了模型的合理性，对战斗部结构设计或优化提供了一定的理论依据。

1 炸高对射流侵彻的影响

聚能装药与目标之间的距离称之为炸高。炸高对破甲威力的影响较大，一方面随炸高的增加，使射流伸长，从而提高破甲深度；另一方面，随炸高的增加，射流产生径向分散和摆动，延伸到一定程度后产生断裂现象，使破甲深度降低。有利炸高与药型罩锥角、药型罩材料、炸药性能以及有无隔板都有关系。

射流在实际的运动中，直径会随其伸长而缩小，当射流伸长到一定长度后，首先在头部出现颈缩和断裂，而后逐渐向尾部，直至射流完全断裂。射流断裂后，在空气阻力、断裂扰动和气动力矩的共同作用下，各段射流的距离逐渐增大，并发生翻转。由于各段断裂射流在继续飞行中会发生翻转，从而将严重降低甚至是完全丧失侵彻能力。

可见，选择长且连续的射流侵彻靶板的有利炸高是保证其最大侵彻能力的关键。文中对各不同锥角结构侵彻靶板炸高与侵深关系进行分析，得到装药结构的有利炸高，最大限度发挥射流的侵彻威力。

2 数值仿真模型

2.1 装药结构模型

药型罩材料为紫铜，炸药为B炸药。装药结构如图1所示，其中：D为装药直径，t为药型罩壁厚；l为起爆点到药型罩锥顶的距离，l＝D／2；β／2为锥角。在这里 D＝40 mm，l＝40，β分别取40°、45°、50°、55°、60°、65°。

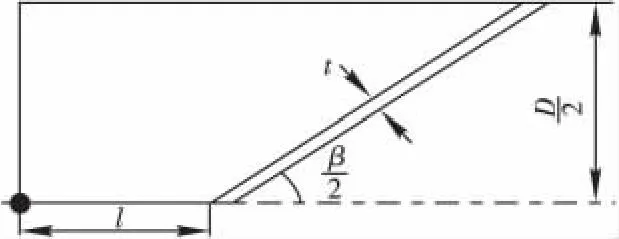
图1 装药结构图

2.2 材料模型

材料模型选择AUTODYN自带的材料模型进行处理，涉及到空气、炸药、紫铜和钢等4种材料模型。其中：空气采用理想气体模型，其状态方程为：

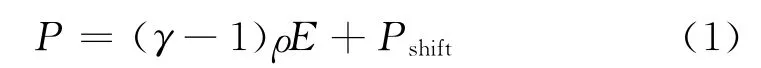
式中：气体常数γ＝1.4；密度ρ＝1.225e－3 g／c m3；内能E＝2.0664e－6；初始压力Pshift＝0。

炸药采用标准J WL状态方程，其形式为：

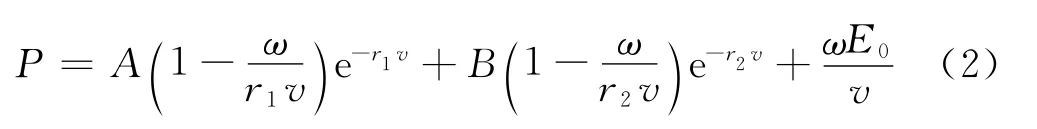
式中：密度ρ＝1.717 g／c m3；参数A＝5.2423，B＝0.7678，r1＝4.2，r2＝1.1，ω ＝0.34；爆速v＝7980 m／s。

紫铜采用Shock状态方程，其形式为：

式中：c0和s是定义Us和Up的关系系数，Us＝c0＋sUp；其中，Us是冲击波速度，Up是冲击波波阵面上的质点速度。密度ρ＝8.96 g／c m3；γ0＝1.99。

2.3 计算模型

由于所研究问题具有对称性，在模拟计算中采用对称面的方法，计算域网格按轴向等间距（每格0.5 mm），径向变间距划分（靠近轴线取80格，每格0.5 mm），为了避免应力在边界反射，设置边界条件时，设为“Flow－out（All equal）”，即所有物质可以正常流出边界，而且应力波也会无反射的传播出去。

图2 45°锥角轴对称数值计算模型

2.4 算法选择

对于聚能射流形成这类涉及高应变率的问题，Lagrange算法往往由于网格的畸变、扭曲及相互间的叠置从而导致计算的失败，而Euler网格则很容易实现这一问题的求解。文中炸药、药型罩和空气3种材料采用Euler处理器建模。壳体和靶板采用Lagrange处理器建模，将靶板的Lagrange单元定义为固体，将炸药、空气和药型罩的多物质Euler单元定义为流体。

3 仿真结果及分析

3.1 仿真结果

取炸高分别为 40 mm、50 mm、60 mm、70 mm、80 mm、90 mm、100 mm、110 mm和120 mm进行数值计算，得到各种不同条件下的侵彻深度如图3所示。图3显示了药型罩被压垮形成射流以及射流侵入靶板的过程。

图3 聚能装药的射流形成和侵彻靶板过程

经分析和计算得到该装药结构各锥角对应的有利炸高列于表2。不同锥角的炸高和破甲深度如图4所示。

图4 不同锥角的炸高和破甲深度曲线图

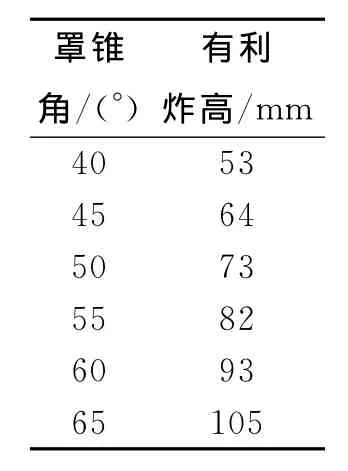
表1 不同药型罩锥角对应的有利炸高

3.2 结果分析

从图4和表1中可以明显看出：对应于每一种装药和锥孔结构有一个最佳炸高，在一定锥角范围内，锥顶角愈小，最佳破甲深度的炸高愈小，射流的有利炸高随着锥角的增加而增加。分析其主要原因是随着锥角减小，形成射流时间比较短，射流自由运动时其纵向存在速度梯度增加，在相对较小的炸高上就能形成长且连续的射流。同时射流拉伸比较剧烈，形成细而长射流，侵彻能力比较强。而当锥角增加，射流速度减慢，在相对较大的炸高上才能形成长且连续的射流，射流断裂位置比较靠后，故有利炸高比较大。

4 结论

文中采用数值仿真的方法分别对不同锥角的药型罩形成射流侵彻钢靶板过程进行了数值模拟和对比分析，得到以下结论：

1）在一定锥角范围内，有利炸高随药型罩锥角增加而增加，此结论与文献［1］得到的结论相一致。

2）不同锥角的炸高和破甲深度曲线图与文献［2］依据试验得出的结论相吻合。

3）在一定范围内，随着药型罩锥角的变大，侵彻深度逐步下降。

［1］ 爆炸及其作用编写组编.爆炸及其作用：下册［M］.北京：国防工业出版社，1979.

［2］ 王艳苹.聚能装药杀伤破甲子弹战斗部装药结构优化设计［D］.南京：南京理工大学，2005.

［3］ 王静，王成，宁建国.射流侵彻混凝土靶的靶体阻力计算模型与数值模拟研究［J］.兵工学报，2008，29（12）：1409－1416.

［4］ 张会锁，赵焊东，王芳，等.药型罩锥角对聚能射流影响的数值模拟［J］.弹箭与制导学报，2005，25（4）：351－353.

［5］ 赵明哲，高兴勇，巩永孝.防护墙抗金属射流侵彻最佳防护距离研究［J］.军械工程学院学报，2009，21（4）；33－35.

［6］ Eitan Hirsch，Joseph E Backoften.Scaling inter national g of the shaped charge jet break－up ti me：A liner t hickness effect observed and explained［C］／／23rd Inter national Sy mposiu m on Ballistics.Tarragona，Spain：The International Ballistics Committee.2007：127－135.