数学归纳法在竞赛解题中的应用
2010-11-23嘉兴市第一中学浙江嘉兴314050
● (嘉兴市第一中学 浙江嘉兴 314050)
数学归纳法在竞赛解题中的应用
●吕峰波(嘉兴市第一中学 浙江嘉兴 314050)
数学归纳法是证明关于正整数n的命题P(n)的重要方法,是通过有限次的验证、假设和论证来代替无限次(或多次)的验证,从而达到严格证明命题的目的.利用数学归纳法证明命题P(n)的步骤是:
(1)证明:当n取第1个值n0时,P(n)成立;
(2)假设当n=k(k∈N*,且k≥n0)时,P(k)成立,证明:当n=k+1时,P(k+1)也成立.
根据(1)和(2)可知,命题P(n)对一切正整数n都成立.
以上又称第一数学归纳法.数学归纳法还具有多种变形,主要有:
变形1(1)证明命题对n=n0(n0≥1)成立;(2)假设命题在n0≤n≤k(k≥n0)时,P(n)成立,能证明n=k+1时命题也成立.根据(1)和(2)可知,命题对一切正整数n都成立.其又称为第二数学归纳法.
变形2(1)证明命题对n=n0+1,n0+2,…,n0+r成立;(2)假设命题在n=k(k≤n0+r)时成立,能推出n=k+r时命题也成立.根据(1)和(2)可知,命题对一切正整数n都成立.其又称为跳跃数学归纳法.
变形3(1)证明命题对n=n0(n0为一个固定的正整数)成立;(2)假设命题在n=k(2≤k≤n0)时P(n)成立,能证明n=k-1时命题也成立.根据(1)和(2)可知,命题对不超过n0的一切正整数n都成立.其又称为反向数学归纳法.
数学归纳法风格独特,既有固定的程序,又有极大的灵活性和技巧性.下面对数学归纳法的常用技巧作一些探讨.
1 巧妙添项,配凑形式
例1已知n∈N*,求证:11n+2+122n+1能被133整除.
证明(1)当n=1时,
113+123=1 331+1 728=3 059=133×23,
能被133整除,命题成立.
(2)假设当n=k时命题成立,即11k+2+122k+1能被133整除,则
11k+3+122k+3=
11×(11k+2+122k+1)+122k+3-11×122k+1=
11×(11k+2+122k+1)+122k+1×(122-11)=
11×(11k+2+122k+1)+122k+1×133,
能被133整除,即当n=k+1时命题也成立.
根据(1)和(2),可知命题对n∈N*都成立.
评注在本题中,将11k+2+122k+3变形为
11×(11k+2+122k+1)+122k+3-11×122k+1,
就可以充分运用归纳假设,使问题迎刃而解.
2 大胆尝试,先猜后证
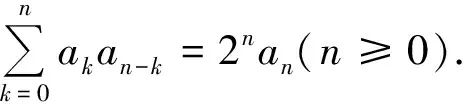



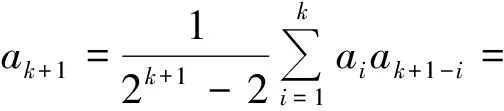
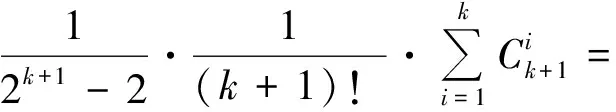

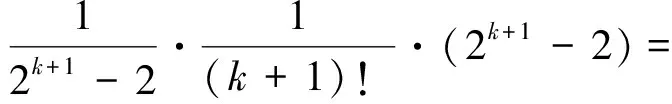

即当n=k+1时,猜想也成立.
根据(1)和(2),可知对一切自然数n,猜想都成立.于是

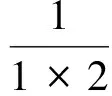

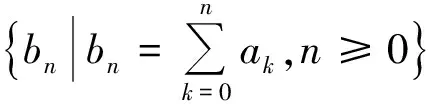

3 增多起点,加大跨度
由归纳假设P(k)成立很难导出P(k+1)成立,但能导出P(k+r)(r≥2)成立时,可以加大跨度,使用跳跃数学归纳法,但相应地就要增多起点.
例3设n∈N*,证明:对所有实数x,有
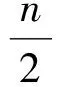
证明(1)当n=0时,左边=|cosx|>0=右边,不等式成立.
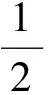
|cosx|+|cos2x|=1-2cos2x+|cosx|=
1+|cosx|(1-2|cosx|)≥

此时不等式成立.
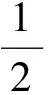
左边=|cosx|+(|cos2x|+|cos4x|+…+
|cos2k·2x|)≥

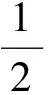
|cosx|+|cos2x|≥1,
因此
左边=(|cosx|+|cos2x|)+(|cos4x|+
…+|cos2k-1·4x|)≥

也就是说当n=k+1时,不等式也成立.
根据(1)和(2),可知不等式对任何n∈N*都成立.
4 有进有退,反向归纳
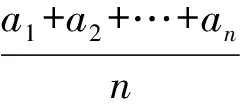
例4证明:对于所有正整数n,

证明考虑数列
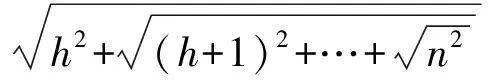
h=n,n-1,…,1.
下面对h用数学归纳法证明:
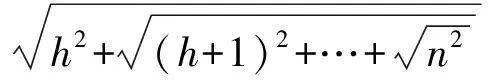
(1)当h=n时,不等式成立,即
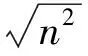
(2)假设当h=k(k≥2)时,不等式成立,即
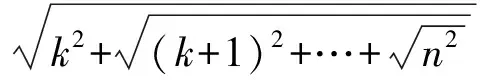
则当h=k-1时,

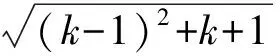
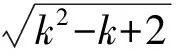

特别地,对h=1,有bn<1+1=2.
评注本题中an和an-1并无简单的递推关系,于是固定了n,转而考虑数列
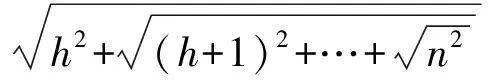
其中h由n减少到1(虽然bn的下标由1增至n).
5 合理归纳,选好对象
例5在m×n的格子纸中填入mn个两两不同的数字,用红笔圈出每行最大的s个数,用蓝笔圈出每列最大的t个数,那么至少有st个数同时被红蓝笔圈出.
证明对s+t用数学归纳法.
(1)当s+t=2时,s=t=1,结论成立,因为最大的一个数一定同时被红蓝笔圈出.
(2)假设当s+t=k时结论成立,则当s+t=k+1时,分情况讨论:
①若在某一行中有s个数同时被红蓝笔圈出,则将这行删去,在剩下的表中用黄笔圈出每列中最大的t-1个数(注意:被黄笔圈出的数必已用蓝笔圈出).由归纳假设可知,至少有s(t-1)个数同时被红黄笔圈出.再加上被删去的一行的s个同时被红蓝笔圈出的数,格子纸中同时被红蓝笔圈出的数至少有st个.
②若在某一列中有t个数同时被红蓝笔圈出,则同理可证.
下面证明,情况①和情况②必有一种成立.
把格子纸中所有填数减序排列记为b1,b2,…,bmn,显然b1同时被红蓝笔圈出,记第1个不被红笔和蓝笔圈出的数为br.若br不被红笔圈出,则与br同行的数至少有s个比br大,于是由br的定义可知,这s个数全被红蓝笔圈出;若br不被蓝笔圈出,则与br同列的数至少有t个比br大,于是这t个数全被红蓝笔圈出.
根据(1)和(2),可知结论成立.
评注对于与正整数s,t有关的命题,常用的思考方法是对s,t或者s+t进行归纳.
6 曲中求伸,强化命题
有些命题P(n)直接用数学归纳法处理时,难以实现从n到n+1的过渡;然而比P(n)更强的命题Q(n),用数学归纳法证明时反显简单,因此需要对原命题给予加强.
例6已知n∈N*,求证:
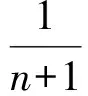
证明用数学归纳法证明不等式:
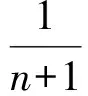
(1)当n=1时,

不等式成立.
(2)假设当n=k时,不等式成立,即

则当n=k+1时,
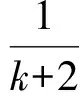
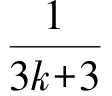
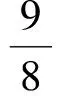

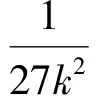
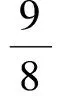
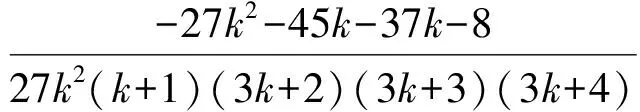
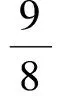
即当n=k+1时不等式也成立.
根据(1)和(2),可知不等式对任何n∈N*都成立.
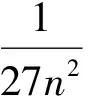
7 欲擒故纵,推广命题
对仅与某些较大的正整数有关的命题,可以考虑把它推广到任意正整数n,再用数学归纳法证明推广后的命题.这种“欲擒故纵”的解题策略也可以解决数学竞赛中的许多问题.
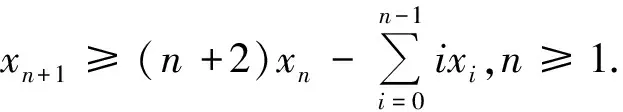
证明用数学归纳法证明:对n≥1,有不等式
(1)当n=1时,x2≥3x1>x1=a.
(2)假设不等式对不大于k的数都成立,则
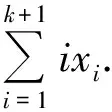
更进一步,由x1>0,得x2,x3,…,xk>0,于是
xk+2>(k+1)xk+1>(k+1)(a·k!).
根据(1)和(2),可知
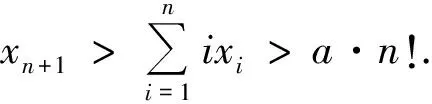
于是,对足够大的n,有xn+1>a·n!>2 010!.
8 孪生命题,螺旋归纳
在命题论证中,有时会出现一个命题的2个部分“跷跷板式连环相套”的现象.对付这种现象的一种办法就是:将原来对一个命题的证明,变为跷跷板归纳式的同时证明一对孪生命题.这种归纳证明的方法也称为螺旋归纳法.
例8证明:在斐波那契数列中,有

(1)当n=1时,在P(n)中,
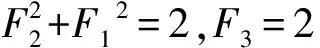
在Q(n)中,
因此等式P(n)和Q(n)都成立.

F2k+1+F2k+2=F2k+3,
F2k+2+F2k+3=F2k+4.
也就是说当n=k+1时,等式P(n)和Q(n)都成立.
根据(1)和(2),可知等式P(n)和Q(n)对任何n∈N*都成立.
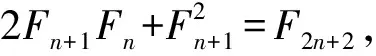
9 弱化命题,以退求进
数学归纳法的另外一种命题转化形式是:先证一个比原命题弱的命题;然后以此为基础,再去证明原命题.弱化命题能起到减弱证明难度、分散证明难点,实现以退求进的作用.
例9函数f(x)是定义在正整数上且取值为正整数的函数,有f(n+1)>f(f(n)),证明:对一切正整数n,都有f(n)=n.
证明先用数学归纳法证明一个较弱的命题:已知m,n∈N*,若m≥n,则
(1)当n=1时,对一切正整数m≥1,都有f(m)≥1,因此式(1)成立.
(2)假设当n=k时,式(1)成立.即若m≥k,则f(m)≥k,m,k∈N*.从而当m≥k+1时,由m-1≥k,得
f(m-1)≥k.
又由f(m-1)∈N*,得
f(f(m-1))≥k,
于是
f(m)>f(f(m-1))≥k.
又因为f(m)∈N*,所以f(m)≥k+1,也就是说当n=k+1时,式(1)也成立.
根据(1)和(2),可知式(1)对任何m≥n(m,n∈N*)都成立.
令m=n,即f(n)≥n,则
f(n)≤f(f(n)) 于是函数f(x)在正整数集上单调递增,从而 n≤f(n) 又因为f(n)∈N*,所以f(n)=n. 评注本题中的条件以不等式的形式给出,而结论以等式的面目给出,难以一步证明成功,因此考虑弱化命题. [1] 苏淳.漫话数学归纳法的应用技巧[M].合肥:中国科学技术大学出版社,1992.
