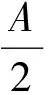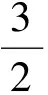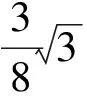简述三角变换与构造法在三角问题中的应用

● (鉴湖中学 浙江绍兴 312030)

简述三角变换与构造法在三角问题中的应用

●胡惠根(鉴湖中学 浙江绍兴 312030)

三角变换方法灵活且多样，而构造法在三角中的应用更是常被人遗忘.本文举例阐述三角变换与构造法的一些应用.

1 通过构造函数、构造图形等途径来解三角问题

例1已知a1cosα1+a2cosα2+…+ancosαn=0，a1cos(α1+1)+a2cos(α2+1)+…+ancos(αn+1)=0，求证：对任意的β∈R,恒有a1cos(α1+β)+a2cos(α2+β)+…+ancos(αn+β)=0.

f(0)=f(1)=0，

因此

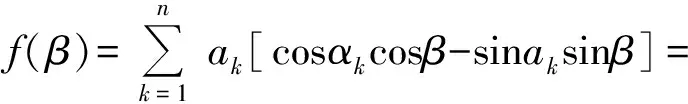
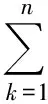
(1)

取β=1，得

例2求满足下式的锐角x：

解将原式变为余弦定理的形式：

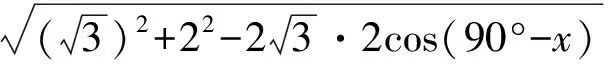
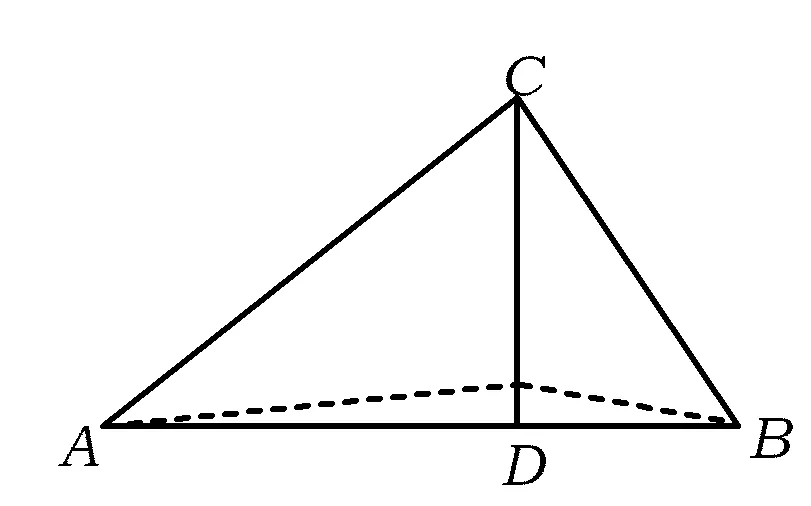
图1

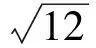
依题意有AD+DB=4，连结AB，在Rt△ABC中，

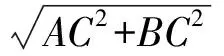
因此点D在AB上.由S△ACD+S△BCD=S△ABC，可得

即

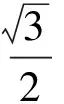
于是

sin(30°+x)=1.

又由x是锐角，得

30°+x=90°，

因此

x=60°.

2 运用三角公式代换，套用三角公式解决问题

三角公式在表达上具有各种不同的特点.这些特点使我们能够运用三角换元法，将其他数学问题转化为三角问题,并充分发挥三角公式的特点解决问题.

( )

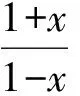
解令x=tanα，则

因此

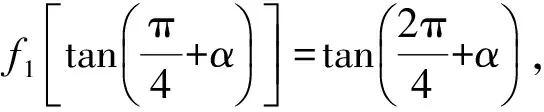
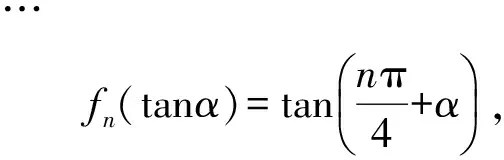
于是

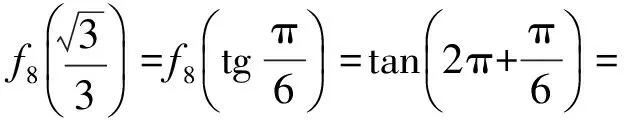
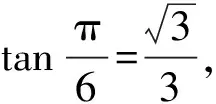
故选D.

例4已知集合A={(x，y)|9x2+36y2≤144}，B={k|k2+5=ak+2b，(a，b)∈A}，求集合B.

分析按照题意，即要求关于k的二次方程k2+5=ak+2b且9a2+36b2≤144的解集.如何恰当地运用条件9a2+36b2≤144成为解决本题的首要目标.若将条件改写为9a2+36b2=t2≤144，对比sin2a+cos2a=1，则容易看出此条件宜用三角方法描述，由此得出如下解法.

解由(a，b)∈A，得

9a2+36b2≤144.

即

3k2-tkcosa+15-tsina=0，

因此

Δ=t2cos2a-12(15-tsina)=

-(144-t2)-(tsina-6)2.

因为

144-t2≥0，(tsina-6)2≥0，

因此

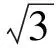
3 形式类比，通过构造公式解决问题

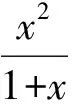
(2005年全国高中联赛加试试题)

解法1由条件得

b(az+cx-b)+c(bx+ay-c)-a(cy+bz-a)=0，

即

2bcx+a2-b2-c2=0,

得

同理可得

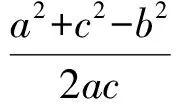
由a，b，c，x，y，z为正数,知

b2+c2>a2，a2+c2>b2，a2+b2>c2，

因此可构造一个以a，b，c为边长的锐角三角形ABC,其中

x=cosA，y=cosB，z=cosC，

于是问题就可转化为：在锐角△ABC中，求函数

f(cosA，cosB，cosC)=

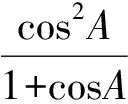
的最小值.因为

tanA+tanB+tanC=tanAtanBtanC，

所以

cotBcotC+cotAcotC+cotAcotB=1.

令μ=cotA，υ=cotB，ω=cotC，则μ，υ，ω∈R+，代入可得

μυ+υω+ωμ=1，

且

μ2+1=(μ+υ)(μ+ω)，

υ2+1=(μ+υ)(υ+ω)，

ω2+1=(μ+ω)(υ+ω).

又由μ=cotA,得

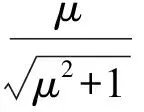
因此

同理可得

于是

(υ2-υω+ω2)+(μ2-μω+ω2)]=

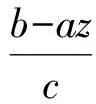
将以上2个式子代入bx+ay=c,得

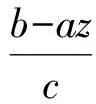
即

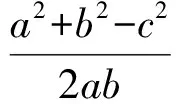
同理可得

以下同解法1.

除课本中的公式外，还有以下一些常用的三角恒等式、三角不等式：

(1)tanAtanBtanC=tanA+tanB+tanC；

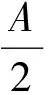
(3)sin2A+sin2B+sin2C=2+2cosAcosBcosC；

(6)cos2A+cos2B+cos2C=1-2cosAcosBcosC；