例谈不等式问题中的代换方法
2010-11-23南菁高级中学江苏江阴214437
● (南菁高级中学 江苏江阴 214437)
例谈不等式问题中的代换方法
●陈培东(南菁高级中学 江苏江阴 214437)
不等式问题是考试中永恒的热点,值得重视与关注.不等式问题往往难度较大,需要一些常规方法以外的补充.本文通过实例分析介绍不等式问题中的若干代换方法.
1 整体代换
常为简化代数式的某关键或困难部分,譬如分母、被开方式等作整体代换.

分析题目中不等式为线性齐次式,可通过整体代换来简化分母,使得基本不等式有用武之地.
解设x=a+2b+c,y=a+b+2c,z=a+b+3c,则
c=z-y,b=x-2y+z,a+3c=2y-x,
从而


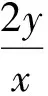

2 比例代换

例2设a,b,c∈R+,且abc=1,求证:

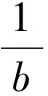
同理可得
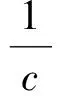
因而
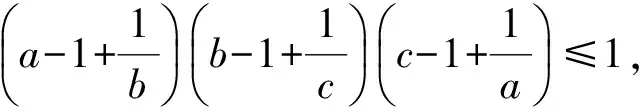
等价于
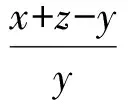
即
(x+z-y)(x+y-z)(y+z-x)≤xyz.
由题意可知,x+z-y,x+y-z,y+z-x至多有一个小于0.
若只有一个小于0,则左边小于0,右边大于0,不等式显然成立.
若x+z-y,x+y-z,y+z-x都是正数,则
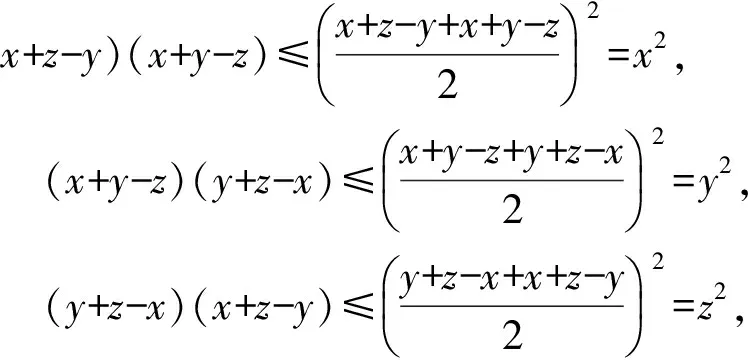
因此
(x+z-y)(x+y-z)(y+z-x)≤xyz,
即原不等式成立.
3 三角代换
当算式某部分的结构与某三角公式的形式类似时,易想到尝试三角代换解题.
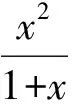
分析由cy+bz=a,az+cx=b,bx+ay=c,可得
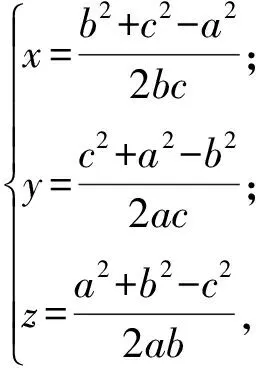
此式具有余弦定理的结构,暗示可作三角换元.
解答过程请参见本期第13页.
4 增量代换
当题设中各量之间具有某种大小关系时,可以采用增量代换的方法处理.
例4求最大的实数k,使得对任何满足u2>4vw的正实数u,v,w,不等式
(u2-4vw)2>k(2v2-uw)(2w2-uv)
都成立,并证明你的结论.
当前,我国医疗事业取得了长足进步,人们生活水平和社会服务条件进一步提高。在这样的大背景下,医疗卫生的要求也提升,各大医院必须不断提高服务水平与服务质量,才能满足民众的需求。加强内部控制是提高医院竞争力的重要举措,但在当前医院财务会计内部控制的工作中依旧存在不少问题,直接对财务控制效果产生影响,因此必须得到越来越多工作人员的高度重视。
分析注意到不等式关于v,w对称,且为齐次式,可取v=w=1,u=2+t(t>0),则不等式(4t+t2)2>kt2恒成立,即k<(4+t)2恒成立,故k的最大值为16.
解可取v=w=1,u=2+t(t>0),则不等式即为(4t+t2)2>kt2恒成立,即k<(4+t)2恒成立,因此k≤16.
以下再证:(u2-4vw)2>16(2v2-uw)(2w2-uv)恒成立.

(u2-4vw)2>16(2v2-uw)(2w2-uv)
等价于
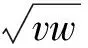
即
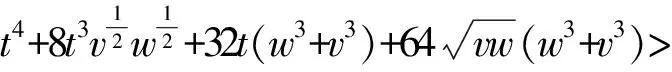
(1)
注意到
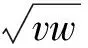
5 常数代换
对于齐次对称不等式,可以设一个齐次对称式为常数,从而使问题得到简化.
例5(卡尔松不等式)已知a,b,c∈R+,求证:

分析不等式为齐次对称不等式,可设ab+bc+ca=3,则不等式可简化为
(a+b)(b+c)(c+a)≥8.
证明注意到待证不等式为齐次对称不等式,不妨设ab+bc+ca=3,则只需证明
(a+b)(b+c)(c+a)≥8.
注意到
(a+b)(b+c)(c+a)=
(a+b+c)(ab+bc+ca)-abc,
则只需证明
3(a+b+c)≥8+abc.
由

可得
abc≤1,
因此a+b+c≥3等价于
(a+b+c)2≥3(ab+bc+ca),
最后一式是显然的,故原不等式得证.
6 内切圆代换
当不等式中字母表示三角形的边长时,可用内切圆代换a=x+y,b=y+z,c=z+x,使问题变为正实数范围内的无另加条件的不等式.
例6已知x,y,z∈R+,xyz=1,且x(1+z)>1,y(1+x)>1,z(1+y)>1,求证:
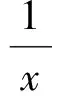
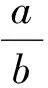
即
2(a2c+ab2+bc2)≥b2c+ac2+a2b+3abc.
(2)
由x(1+z)>1等价于

即
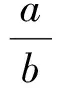
得
a+c>b.
同理可得
b+c>a,a+b>c.
故a,b,c可作为三角形的3条边,作内切圆的替换
a=m+n,b=n+t,c=t+m,m,n,t∈R+,
从而式(2)即为
2∑(n+t)(t+m)2≥
∑(n+t)2(t+m)+(m+n)(n+t)(t+m),
因此
2∑m3+6∑m2n+4∑mn2+12mnt≥
∑m3+5∑m2n+6∑mn2+12mnt,
即
∑m3+∑m2n≥2∑mn2.
最后一式由
m3+t2m≥2tm2,n3+m2n≥2mn2,t3+n2t≥2nt2
可得到,故不等式得证.
