短缺部分拖后的变质性物品的联合定价与订货模型

赵 林, 俞能福

(安徽建筑工业学院 数理系,安徽 合肥 230601)

0 引 言

在实际的市场运行中,当销售商降低某些商品的零售价格时,这些商品的销量明显增加,而当调高零售价格时,这些商品的销量明显减少,有的甚至处于滞销状态,这说明销售商的销售价格对市场需求往往具有决定性的影响。因此,如何制定合理的销售价格,在刺激需求的同时也使得自身的销售利润达到最大化,是每个销售商所面临的实际问题。尤其在当前,随着生产能力的大幅提升和市场竞争的日益加剧,制定适宜的价格策略以获取最大收益显得尤为重要。

近年来,需求依赖销售价格的库存控制问题引起了众多企业和研究者关注。文献[1]首次从定量的角度建立了需求受销售价格影响的最优订购批量和销售价格联合决策模型。文献[2]则考虑了在供应商提供临时价格折扣下,销售商的最优订购批量和销售价格联合决策问题。文献[3]则在假定需求具有价格弹性情形下,发展了一个允许滞后支付的最优订购批量和销售价格联合决策模型。文献[4,5]考虑了带有运输费用折扣的最优售价和订购批量的联合确定问题。以上模型均不考虑短缺,文献[6]则探讨了短缺部分拖后的变质性物品最优订购批量和销售价格联合确定问题,在其模型中假定变质率是随时间变化而变化,且如果短缺量部分拖后,通常认为在缺货期间的拖后需求率是顾客等待时间的减函数,即等待时间越长,短缺量拖后率越小。

但在实际的零售过程中还会常常遇到一些顾客对某一商店有特别偏好(由于该商店的声誉,或者商品质量等原因),当商店缺货时他们愿意等待,但同时顾客往往都无足够的耐心,随着缺货时间的增加他们就会对库存系统是否能够及时供货缺乏信心,另外,缺货时间越长则前面排队等待供货的人就会越多,这也在一定程度上影响了顾客愿意等待供货信念,因而转往其他销售商处购买商品。从这种意义上来说,缺货时间越长,则愿意等待供货的顾客就会越少,即短缺量拖后率是随缺货时间变化的[7]。

因此本文将短缺量拖后率看成是缺货时间的下降函数,以此来逼近这一实际现象,从而建立了一种需求受价格影响且短缺量部分拖后的变质性物品的库存控制模型,其中物品的变质速度是随时间变化而变化的。

1 符号及模型假设

为了更方便地研究和说明库存模型,统一规定如下符号:

K为每周期订货的订货费;c为单位商品的购买价格;p为单位商品的销售价格;h为单位商品单位时间内的库存保管费;s为单位商品单位时间内的缺货费用;π为因缺货造成销售损失的单位商品的机会成本;t1为一个订货周期内不缺货的周期长度;T为一个订货周期的长度;I(t)为t时刻的库存水平;q为每周期的销售量;Q为每周期的订货量;Π(p,T,t1)为该库存系统的平均利润。

另外为了更符合实际,本文作了如下假设:①备运期为零;②p＞c;③t时刻的需求率d(p)是关于p的非负的、连续的递减的严格凸函数;④假定变质率为θ(t),其中0＜θ(t)≪1,且物品变质后无残值;⑤允许短缺且短缺部分拖后。假定缺货期间发生的需求仅有一部分人愿意等待,等待比例随缺货时间(或者缺货量)的增加而减少,假设该比例函数(即需求拖后率函数)为e-β(t-t1),其中 ,t1≤t≤T,0 ＜β＜1。

2 模型的建立

根据以上假设,库存水平变化如图1所示。为了建立合适的利润函数,把周期分为2个相对独立的区间[0,t1)和[t1,T)。在区间[0,t1)中,库存水平受需求和变质2个因素的影响而减少,因此库存水平可由下述微分方程描述:

由边界条件I(t1)=0解得(1)式为:

图1 库存水平变化示意图

由(2)式可得每个周期最大库存水平为:

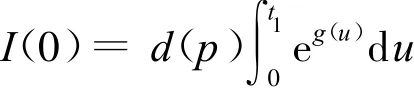
在区间[t1,T)内,可用如下微分方程描述:

由边界条件I(t1)=0解得(3)式为:

在(4)式中令t=T,可得每周期内拖后需求的最大量为:

因此,每周期的订货量为:

每周期销售量为:

很明显,一个周期内的利润函数应由以下几部分函数构成:

(1)每周期订货费用为K;

(2)每周期库存保管费用,且有:

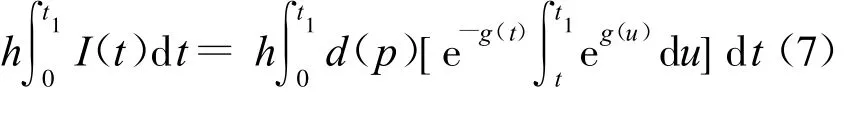
(3)每周期的短缺费用,且有:

(4)每周期因为损失销售而造成的机会成本:

(5)每周期的购买费用,且有:

(6)每周期的销售收入,且有:

因此该系统单位时间内平均利润函数(即目标函数)为:

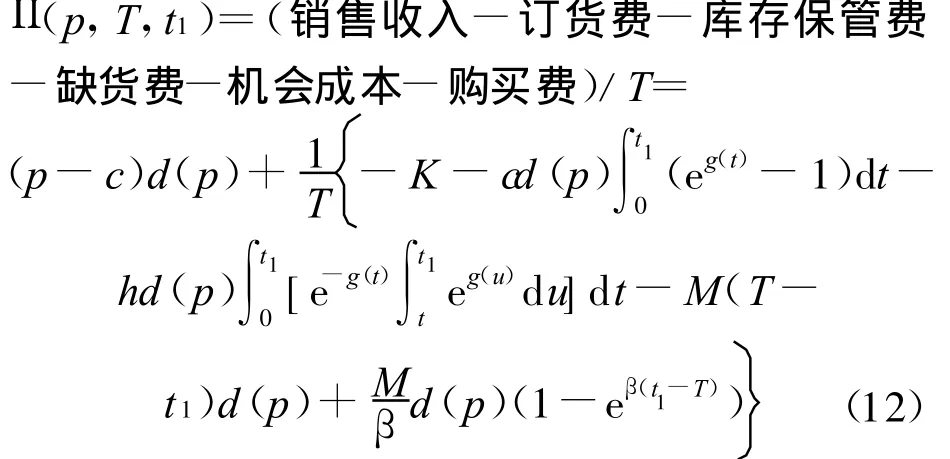
3 求解模型

定理1 只要λ＞0,且(p-c)d(p)是关于价格p的严格凹函数,则最优化问题max Π(p,T,t1)存在惟一最优解,否则其最优解不存在。其中

证明 为了方便,首先把价格 p看成已知的,只讨论 T和t1的最优值问题。因为 Π(p,T,)是可导的,所以其最优值点一定满足显然

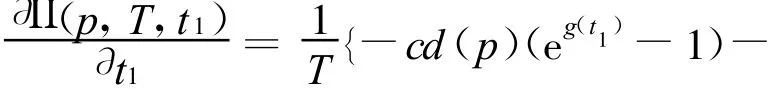
对(13)式再求导可得:

亦即:

用(16)式简化(12)式得目标函数的另一种形式,即利润函数是只关于T的一元函数,则有:

其中,t1=t1(T),由(16)式惟一确定。

根据隐函数求导法则,由(15)式得:

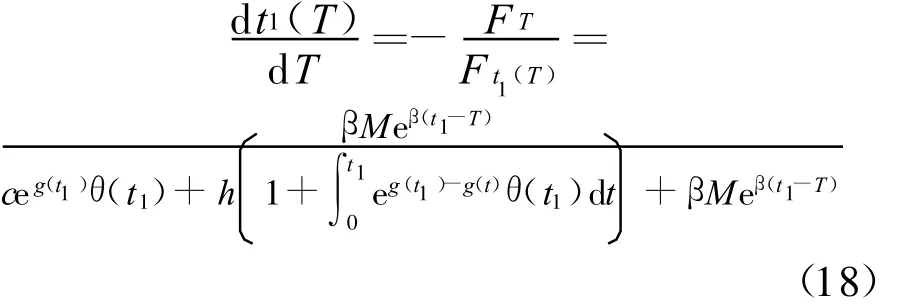
为了方便,先记

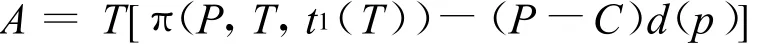
所以

用(16)式化简(19)式可得:

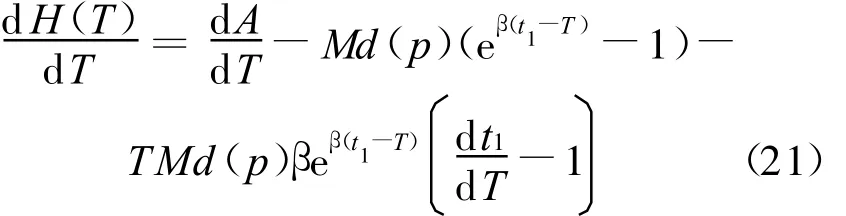
易知:

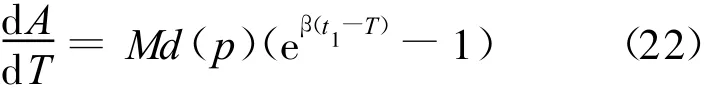
用(16)式、(22)式对(21)式化简可将其等价变形为:

若λ＞0,根据根的存在性定理知在(0,+∞)内,必然存在惟一的根T*满足H(T*)=0,从而在

所以平均利润函数 Π(p,T,t1)是关于 T的局部上凸函数,即关于T的局部凹函数。注意到驻点T*的惟一性,因此函数Π(p,T,t1)必然是一个单峰函数,从而(T*,t*1)是 问题 max Π(p,T,t1(T))的惟一最优值点,其中 t*1=t1(T*)由(16)式惟一确定。

则 Π(p,T,t1(T))在区间 T∈(0,+∞)内是严格递增的,优化问题 max Π(p,T,t1(T))在区间T∈(0,+∞)内无最优解。

通过分析可知,只要λ＞0,则对任意给定的价格p(p＞0),使 Π(p,T,t1(T))取得最大值的点(T*,t1*)存在且惟一。给定(T*,t1*),则平均利润函数是关于p的一元函数,若求p的最优解,则必然满足所以有:

假设(p-c)d(p)是关于价格的严格凹函数,这意味着其2阶导数2d′(p)+(p-c)d′(p)＜0,又d(p)是关于价格p的连续递减的严格凸函数,所以d″(p)＞0。因此有:

即证明平均利润函数是关于价格 p的严格凹函数,因此存在一个满足(25)式的最优定价,即销售价格的最大之值p*。

方程 d(p)+(p-c)d′(p)=0 的解pl,是 最优定价 p*的最低限,其中 p*满足

4 实际案例

一个电动机批发商,所经营的电动机种类繁多,适用于各种用途和各种工业环境(从操作高架起重机到电动喷漆设备)。该公司在四川省内(成都、重庆和乐山)设有3个分公司,各分公司经理具有各自区域内完全的利润责任。

利润率的重要部分取决于交付系统的有效管理。由于该公司经营的是批发业务,因此存货成本为该公司总营运成本的重要部分。针对其中一种电动机进行研究,确定其最优的订货周期和零售价格。

假设该公司每次订购此种电动机所产生的K=100元/周期,c=10元/单位商品,h=1元,s=2元/(单位商品◦单位时间),π=2元,允许短缺且短缺部分拖后。假定缺货期间发生的需求仅有一部分顾客愿意等待,等待比例随缺货时间(或者缺货量)的增加而减少,假设该比例函数(即需求拖后率函数)为 e-β(t-t1),其中 β=0.5。另外由于产品的更新速度较快,产品的折旧率(相当于变质率)θ(t)=0.1t,而经过市场调研得知该种电动机的市场需求受到其零售价格影响,且其需求函数近似为d(p)=p-2。

通过解方程d(p)+(p-c)d′(p)=0,得到pl=p0=20,然后联立H(T*)=0和(16)式可以求出该种电动机的最优订货周期为T*=0.828 1和最优有货区间是t1*=0.282 6,这说明适当的缺货对于该种电动机的销售是有利的。再将T*和t1*代入(25)式求出该种电动机的最优市场零售价格为p*=22。

5 结束语

本文主要研究了一类短缺量拖后率随缺货时间变化而变化的变质性物品的库存模型,其中物品的需求受销售价格的影响且物品的变质速度随时间而变化。

首先在给定价格的条件下给出了最优订货周期存在的必要条件,再假设最优订货周期给出的条件下求出最优价格,并指出了模型解的存在性与惟一性,最后用实例说明了模型的可行性。

本模型可进一步推广到考虑量折扣和时变需求的情形。

[1] Kunreuther H,Richard J F.Optimal pricing and inventory decisions for non-seasonal items[J].Econometrica,1971,39:173-175.

[2] Abad P L.Optimal policy for a reseller when the supplier offers a temporary reduction in price[J].Decision Science,1997,28:637-653.

[3] Shinn S.Determining optimal retail price and lot size under day-terms supplier credit[J].Computer and Industrial Engineering,1997,33(3/4):717-720.

[4] Burwell T H,Dave D S,Fitzpatrick K E,et al.Economic lot size model for price dependent demand under quantity and freight discounts[J].International Journal of Production E-conomics,1997,48:141—155.

[5] Abad P L,Aggarwalb V.Incorporating transport cost in the lot size and pricing decisions with downward sloping demand[J].International Journal of Production Economics,2005,95:297-305.

[6] Abad P L.Optimal price and order size fo r a reseller under partial backordering[J].Computers and Operations Research,2001,28:53-65.

[7] Min Jie,Zhou Yongwu,Zhao Ju.An inventory model for perishable items with maximum customer waiting time under inflation[J].应用数学,2007,20(4):688-696.